Assignment 9: SMT 1
------

:::info
In this assignment, you will:

- Create your first SMT formulas to model systems examples.
- Practice using the SMT theories for mathematical integers and fixed-width machine bitvector integers.
- Use the z3 library in Python (or in Rust) to check the equivalence between different system implementations.
:::

This is a **pair assignment**—you may choose to either complete the assignment alone or with one other CS340 classmate. On Gradescope, you will be able to form a group with maximum size 2.

# Setup

## Programming language

The default for this assignment is to use the z3 SMT solver as a library in Python (Python 3, specifically). Follow the instructions from class to install the z3 library on your local machine.

You may opt to instead use the Rust by using either the [smtlib](https://docs.rs/smtlib/latest/smtlib/) or [easy-smt](https://docs.rs/easy-smt/latest/easy_smt/) libraries (though neither provides operator overloading). For this assignment, doing so does not earn extra credit, but it may be useful if you'd like to continue to practice Rust or if you are interested in conducting research with Alexa in the future (Alexa's research uses `easy-smt`).

:::success
Create two new files, `problems.py` (or a Rust crate) and `README.{md, txt}`. There is no stencil code for this assignment.
:::

### Output format

For this first SMT assignment, just printing the results returned by the z3 library is sufficient (though you should only print a returned instance if one exists).

### Additional resources

Here are references for the z3 interface and Python API.

- [z3Py Guide](https://ericpony.github.io/z3py-tutorial/guide-examples.htm)
- [CMU lecture notes (including common Python API calls)](https://www.cs.cmu.edu/~aldrich/courses/17-355-19sp/resources/recitation08-notes.pdf)
- [z3 Tutorial](http://theory.stanford.edu/~nikolaj/programmingz3.html)

# Problem 1

Alice thinks that there might be some non-negative number whose negation is also non-negative.

:::success
Create two functions named `non_negative_negation_int` and `non_negative_negation_bitvec` to find such a number, if it exists, for both the theory of integers and the theory of bitvectors. For the theory of bitvectors, use a 32-bit bitvector, like C's `int` type.

**Written Q1** In your README, either answer that no such number exists or provide the number. For the bitvector number, provide your answer in hex with the correct number of bits for its size.
:::

:::info
**Hint:** recall that Python has a built-in `hex()` function that you can use (either in your file or in the Python interpreter) to convert numbers to hex.
:::

# Problem 2

Using her insight from the previous problem, Alice wonders if she can apply some [hacker's delight](https://en.wikipedia.org/wiki/Hacker%27s_Delight) bit-twiddling to implement a [*ternary conditional*](https://en.wikipedia.org/wiki/Ternary_conditional_operator) for C integer types without the using the `?` operator.

She write the following C code:

// Try to implement x ? y : z with bit-twiddling
int wacky_conditional(int x, int y, int z) {
   int i = ((-x|x) >> 31);
   return (y & i) | (z & ~i);
}

:::success
Create a new function, `wacky_conditional`, and use z3 to determine whether or not Alice's conditional representation is equivalent to `x ? y : z`.

**Written Q2** In your README, say whether or not Alice's function is equivalent. In your own words, describe why the SMT constraints your wrote answer the equivalence question for *any* 32-bit `x`, `y`, and `z`.

**Written Q3** What have you proven about Alice's implementation?
:::

:::info
**Hint**: the ternary operator in Python's z3 library is named `If` (but it requires the first argument to be a boolean).
:::

# Problem 3

A [`NAND` (not and) logical gate](https://en.wikipedia.org/wiki/NAND_gate#:~:text=In%20digital%20electronics%2C%20a%20NAND,HIGH%20(1)%20output%20results.) is a commonly-used low-level circuit building block because is a *universal gate* that can be implemented efficiently with a small number of transistors.

One of the following two circuits correctly implements [`XOR` (exclusive or)](https://en.wikipedia.org/wiki/Exclusive_or) using `NAND` gates and `NOT` gates.


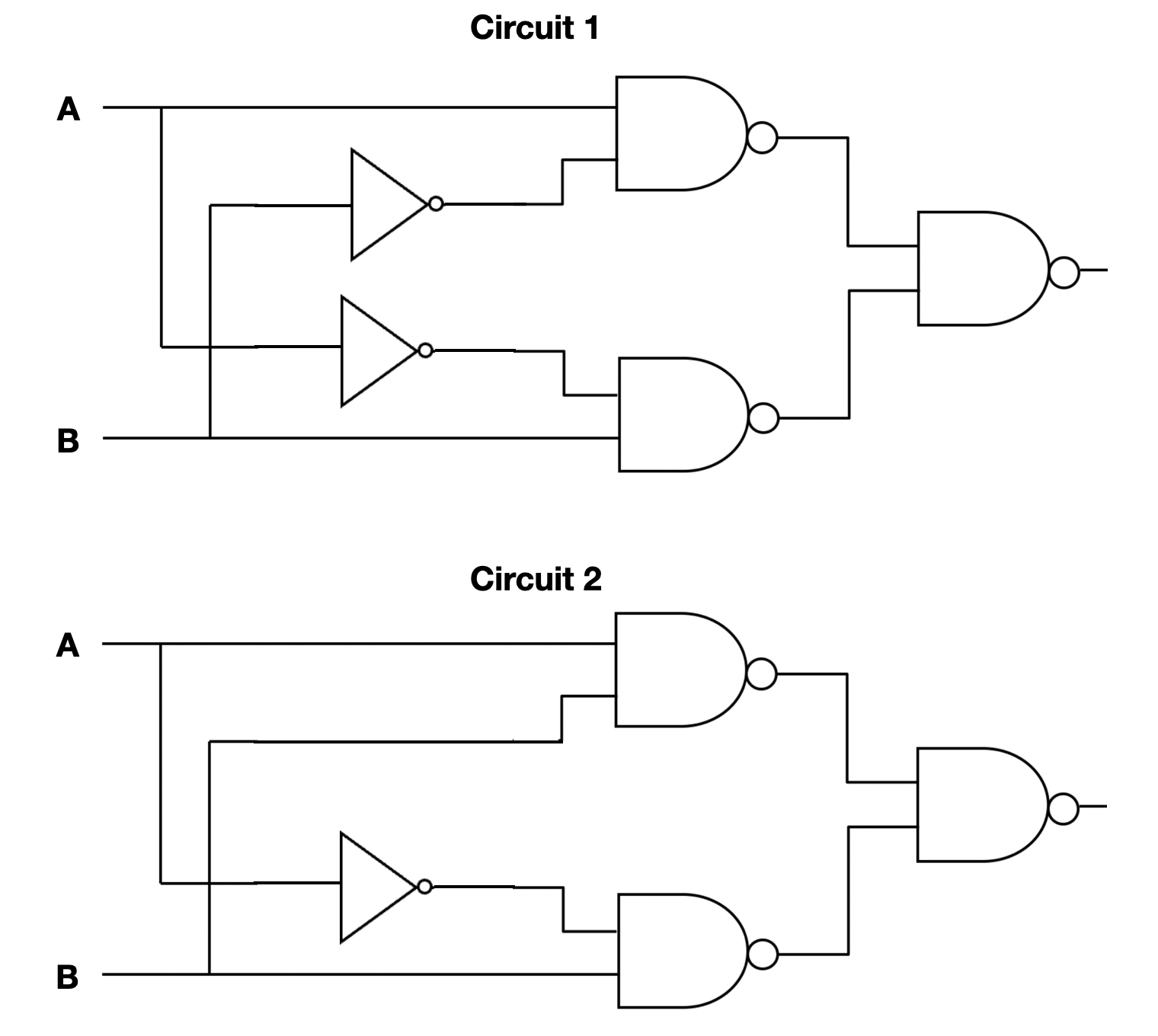
:::success
Create two functions, `nand_circuit1` and `nand_circuit2`, and use z3 to show that one circuit is equivalent to `XOR` and one circuit is not equivalent to `XOR`.

**Written Q4** In your README, say which circuit is equivalent. For the circuit that is not equivalent, describe a concrete counterexample and explain what the expected result is and what the circuit incorrectly produces instead.
:::

:::info
**Hint**: z3 does not have `NAND` built in, but you can model it with `Not(And(..., ...)`.
:::

# Problem 4

Recall the 4-bit Arithmetic Logic Unit (ALU) from [CS240](https://cs.wellesley.edu/~cs240/s25/assignments/arch/#q2-value-judgments-28-points):

This ALU supports arithmetic operations on two signed, two's complement 4-bit inputs, $A_3A_2A_1A_0$ and $B_3B_2B_1B_0$.

In more detail, each bit has a circuit that is designed like so:

## Part 1
:::success
Use Z3 to model this 4-bit ALU. Test your model by showing that for all 4-bit bitvectors `A` and `B`, `A + B` is equivalent to the `Result` of the ALU when `invert A = 0`, `negate B = 0`, `Operation = 10` (e.g., `Operation = 2`).
:::

:::info
**Hints**
- See the [BitVector documentation](https://smt-lib.org/theories-FixedSizeBitVectors.shtml) for more relevant operations. I suggest using 1-bit bitvectors for each bit, then combining them into the full `A`, `B`, and `Result` using the `Concat` operator.
- Use one (or more) if-then-else `If` expressions to model the `MUX` units.
- You can use `+`/`bvadd` on a 1-bit bitvector to model the sum 1-bit adder `[+]` (or, you can model it using `&`, `|`, and `^`). For the carry-out for the 1-bit adder, you can use this formula for 1-bit of carry-out: `carry_out = (((ai ^ bi) & carry_in) | (ai & bi))`.
- Use `Implies` to match the "when" in the problem description.
:::

## Part 2
:::success
Use your model to determine the values of `invert A`, `negate B`, and `operation` that produce `Result = A - B`. Be sure to model this such that the result is correct for all inputs.
:::

:::info
Hint: for this problem, it's fine to use a `ForAll` directly, without any negation.
:::

:::success
**Written Q5** In your README, describe the overall design of your ALU model in a few sentences. State the 4-bit control sequences you found for part 2.
:::

# Problem 5

Three integers $(x, y, z)$ form a [Pythagorean triple](https://en.wikipedia.org/wiki/Pythagorean_triple) if they are positive and $x^2+y^2=z^2$. A way to produce Pythagorean triples is Euclid’s formula. Euclid's formula states that given integers $m$ and $n$ such that $m > n > 0$, $(x, y, z) = (m^2-n^2, 2mn, m^2+n^2)$ is a Pythagorean triple.

## Part 1

:::success
Write a new function, `verify_euclid`, to verify Euclid's formula using the theory of mathematical integers. Verifying the formula means showing that for any choice of $m$ and $n$, the computed $(x, y, z)$ is a Pythagorean triple.
:::

:::info
If your solution is taking a long time (over a minute) to run, you may want to try adding additional constraints. Make sure you have constraints representing each part of the definition of Pythagorean triples and Euclid’s formula as described above.
:::

## Part 2

A triple $(x, y, z)$ is primitive if and only if $x$, $y$, and $z$ share no common factors (other than 1).

:::success
Write a new function, `non_primitive`, to check whether Euclid's formula can produce non-primitive triples.

**Written Q6** In your README, state whether Euclid's formula can produce non-primitive triples (providing a concrete example if applicable).
:::

# Grading

:::success
In your README, also report:
**Written Q7:** Collaborators other than your partner?
**Written Q8:** Roughly how long did this assignment take you (in hours)?
:::

This assignment is worth 100 points, broken down by:

:::info
- 10 points: Problem 1
- 10 points: Problem 2
- 10 points: Problem 3
- 25 points: Problem 4
- 25 points: Problem 5
- 20 points: `README`/**Written Q's 1-7**
:::

# Submission
Submit the following files on Gradescope: `problems.py` and `README.{txt, md}`.

# Attribution

Question 5 is based on a previous version of the [SMT][] assignment from [Tim Nelson's][tim] [Logic for Systems][lfs] at Brown University.

[SMT]: https://docs.google.com/document/u/3/d/e/2PACX-1vTggWSpqnpuh1-EefVab9g_nw13I-zWHGi9RaVowpjEGLSDs9Nz1ejUKu4QBp8l-ZoR9TfSfx0zHcvV/pub
[tim]: https://cs.brown.edu/~tbn/
[lfs]: https://csci1710.github.io/2023/