# iPAS 機器學習考試共筆

[TOC]

---

## 簡介

:::info
**5/21** 考試，大家加油
:::

### 資源分享區https://hackmd.io/CDDXiQkXRQOJEjXqge1kJg?both#L122-%E6%A9%9F%E5%99%A8%E5%AD%B8%E7%BF%92%E8%B3%87%E6%96%99%E5%88%86%E6%9E%90

- Michael 課本：https://leadtek-big-data.slack.com/files/U011V818GQH/F03AXNJE5H8/prml-chinese-edition.pdf
- 題庫： https://www.books.com.tw/products/0010844923
- 4/30 上課：https://youtube.com/playlist?list=PLCtYtQKm1XJxGGXLCd-btVlrSpTVfCzPn 前面睡過頭

## L11

### L111 機器學習工作程序與應用

> Michael 記得把所有你覺得會考試的重點記下來！！！

### L112 機器學習基礎演算法

#### 傑西

##### 樹的演算法
ID3
C4.5
C5.0
CART

##### 決策樹
1. 決策樹(Decision Tree)

1. 原理:
使用樹狀分枝的概念來作為決策模式

2. 定義:
決策樹 是 無母數監督式學習的方法。 用來做分類(Classification)、迴歸(Regression)及多輸出(Multi-output problem)。
>只預測一個值為迴歸、預測兩個值以上為多輸出問題

3. 複雜度:

>基礎知識複習: 複雜度
>大 O 符號：用來描述 演算法在輸入 n 個東西時，所需時間與 n 的關係。
>O(1):不管你輸入多少個東西，程式都會在同一個時間跑完
>O(n):執行步驟會跟著輸入 n 等比例的增加。例如當 n = 8，程式就會在 8 個步驟完成。
>
>Reference:[初學者學演算法｜談什麼是演算法和時間複雜度](https://medium.com/appworks-school/%E5%88%9D%E5%AD%B8%E8%80%85%E5%AD%B8%E6%BC%94%E7%AE%97%E6%B3%95-%E8%AB%87%E4%BB%80%E9%BA%BC%E6%98%AF%E6%BC%94%E7%AE%97%E6%B3%95%E5%92%8C%E6%99%82%E9%96%93%E8%A4%87%E9%9B%9C%E5%BA%A6-b1f6908e4b80)

>基礎知識複習: 樹理論的複雜度
>
>
>N: 節點
>以樹理論來說，d高度:
>最佳d: O(log N) ->Balanced Tree
>最差d: O(N) ->當樹只有一條腳的時候

Decision Tree 複雜度:
N:資料量, k: feature量, d:高度
最佳 O(Nkd) -> O(NK logN)
最差 O(Nkd) -> O(NKN)
Reference:[1.10. Decision Trees](https://scikit-learn.org/stable/modules/tree.html)

> 基礎知識複習:
> 白箱(White Box) - 白箱就是了解人到底是怎麼思考、怎麼推理，讓電腦用和我們大腦思考時一樣的規則來運作，做跟我們一樣有智慧的動作或決定，如：專家系統
> 黑箱(Black Box) - 黑箱則是因為太複雜我們不太清楚，所以有什麼Input它就產生跟我們人很像的Output，如：深度學習

所以 Decision Tree 為 白箱

4. 決策樹模型建置流程

1 .**資料設定**：將原始資料分成兩組，一部分為訓練資料，一部分為測試資料。

2 . **決策樹生成**：使用訓練資料來建立決策樹，而在每一個內部節點，則依據屬性選擇指標來評估選擇哪個屬性(或值)做分支的依據。此又稱節點分割 (Splitting Node)。決定好節點後，用來做成一顆樹。

範例:

3 . **剪枝**：使用測試資料來進行決策樹修剪，防止過度擰合。

將以上1~3步驟不斷重複進行，直到所有的新產生節點都是樹葉節點為止。

[reference: Decision Tree 決策樹簡介](https://jamleecute.web.app/decision-tree-cart-%E6%B1%BA%E7%AD%96%E6%A8%B9/)

5.最大樹建立方法:

CART 使用遞迴方式將資料進行**二元切割**。在每個節點中，CART 會將 資料劃分為兩個子資料集，當每一筆資料都以歸類在同一類別或已經無法找到新的分類進行節點分割時停止。如下：

 createBranch()
 
 檢測資料集中的每個子項是否屬於同一分類：
    if so 
        return 類標籤
    else
　　　尋找劃分資料集的最好特徵 (注)
　　　劃分資料集
　　　建立分支節點
　　　　　　for每個劃分的子集
　　　　　　　　呼叫函式createBranch並增加返回結果到分支節點中
　　　retrun 分支節點
   

(注) 遍歷每一個特徵，遍歷每一個特徵值，如果計算出來資訊增益最大，那麼該特徵就是最佳特徵。

找到最佳的待切分特徵和特徵值呢？   

每個特徵：    
　　每個特徵值：    
　　　　將數據切分成兩份    
　　　　計算切分的誤差    
　　　　如果當前誤差小於當前最小誤差，那麼將當前切分設定爲最佳切分並更新最小誤差   
    
返回最佳切分的特徵和特徵值

連續性的資料: 會先將資料排序，然後以兩值的中間值當作是切分點。使用每個切分點去試算 information gain.

範例一
西瓜紋理

| 紋理3 |根蒂3 |觸感2 |色澤3|
| -------- | -------- | -------- |-------- |
| 清晰 | 捲縮 | 硬滑 |青綠|
| 模糊 | 硬挺 | 軟黏 | 烏黑|
| 不清楚 | 稍捲 | 硬滑 | 淺白|


範例二 連續型的參數 會使用 兩個值的中間值 來劃分

| Start| Age |
| -------- | -------- |
| 15 | 4.5 |
| 9 | 4.7 |
| 8 | 9.3 |
| 7 | 9.1 |
| 4 |10 |


5. 程式及參數:

`class sklearn.tree.DecisionTreeClassifier(*, criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, class_weight=None, ccp_alpha=0.0)`

**criterion{“gini”, “entropy”}, default=”gini”**

Information Gain及Gini Index這兩種方法來選擇節點是最常見的評斷分類的方式:
圖中的資訊來說明，假設我們想預測出喜歡打板球類型的學生，從已知的訓練資料中，系統有下列兩種分類方式如下，何者是較佳的分類呢？


**Information Gain (資訊獲利)- Entropy**
概念:將較高同質性的資料放置於相同的類別，以產生各個節點


Entropy= C:0, A:1
觀念: impurity (不純:屬性值不大相同) /purity(純:屬性值大約相同)

上述例子: Entropy 使用性別分 為 0.86, 使用 班級分為 0.99, 系統會選擇以性別作為節點的分類方式，因為它的Entropy較小。

**Gini Index (吉尼係數)**
GINI係數與INFORMATION GAIN兩者有一個最大的差別：INFORMATION GAIN一次可產生多個不同節點，而GINI係數一次僅能產生兩個，即True或False的Binary分類。

Reference:
https://chtseng.wordpress.com/2017/02/10/%E6%B1%BA%E7%AD%96%E6%A8%B9-decision-trees/

**splitter{“best”, “random”}, default=”best”**
The strategy used to choose the split at each node.
1. Using best會優先選擇更重要的(分數高的)特徵進行分枝
2. Using random
好處:
樹深度更深
對訓練集的擬合會降低(防止過擬合的一種方式)


**max_depth int, default=None**
The maximum depth of the tree. 如果設 none, node會展開到 node底下葉子都是一樣的(分類裡面沒有雜訊) 或是 若有設定 mn_samples_split (一個 node裡面至少要有多少個訓練資料)

**min_samples_split int or float, default=2**
The minimum number of samples required to split an internal node

**min_samples_leaf int or float, default=1**

**min_weight_fraction_leaf**
葉子裡面的 sample 權重加總的最小值。小於這個值會把這個分支去除

**max_features int, float or {“auto”, “sqrt”, “log2”}, default=None**
The number of features to consider when looking for the best split.
注意:如果在設定的考慮特徵數量之內無法找到滿足分裂條件的特徵，那麼決策樹會繼續尋找特徵，直到找到一個滿足分裂條件的特徵

**random_state int, RandomState instance or None, default=None**
用意:隨機選取特徵值

原因:決策樹模型是靠優化節點來建造一棵優化的樹，但最優的節點不一定可以得到最優樹，於是sklearn選擇建不同的樹，然後從中取最好的，在每次分枝時不使用全部特征，隨機選取一部分特征，從中選取不純度相關指標最優的作為分枝用的節點，這樣每次生成的樹也就不同了。當sklearn隨機選擇特征，尤其是當spliter在分枝時多個特征的不純度相關指標一樣時，就會隨機選擇一個作為分枝點，於是官方設計了random_state參數決定特征選擇的隨機性，類似random.seed()保證同一個random_state參數得到的決策樹模型相同，實驗結果可以覆現，便於模型參數調優。

好處:
random_state是用來設置決策樹分枝中隨機模式的參數，在高維度時sklearn決策樹的特徵隨機性會很明顯，低維度的數據（比如鳶尾花數據集），隨機性幾乎不會顯現。高維數據下設置random_state並配合splitter參數可以讓模型穩定下來，保證同一數據集下是決策樹結果可以多次覆現，便於模型參數優化。
Reference[决策树的randomstate参数，到底是干嘛用的?](https://www.zhihu.com/question/358180075/answer/941301081)

**max_leaf_nodes int, default=None**

> 基礎概念
> 樹的成長方式有兩種策略
> 1. Level(Depth)-wise three growth (所有的節點都分裂)
> 
> 2. Leaf-wise (Best-first) (選擇 loss最大的節點 進行分裂)
> 
> 參考[樹類算法之---lightGBM使用與調參](https://www.twblogs.net/a/5ee7a6689b63e9a74dab0b6e)
> 使用: C4.5, CART 使用 DFS，XGBoost使用BFS，SKlean使用 Decision tree classifier 使用 BFS
> 觀念:
> 如果樹長到完整，那兩種策略長出來的樹會一樣，但Leaf-wise可以減少較多的loss。在較少node的狀況下 Leaf-wise perfoemance會比較好。

None:unlimited number of leaf nodes.

**min_impurity_decrease float, default=0.0**
如果這個分裂可以使得不純度>或是=該設定值，節點會被分裂。(貢獻度)

**class_weight dict, list of dict or “balanced”, default=None**
Reference:[How to Improve Class Imbalance using Class Weights in Machine Learning](https://www.analyticsvidhya.com/blog/2020/10/improve-class-imbalance-class-weights/)
解決群數量不平均的問題。可以用 skewed distrinuted 或是 給予不同的加權於 多數 及 少數的群裏面。
用途:在訓練的過程中，在cost function中給 高的權重 予 少數群，會導致 更高的 penalty 給少數群 而讓演算法可以專注於 "減少錯誤" 在少數群裏。

none:群不分大小都是一樣的權重

**ccp_alpha non-negative float, default=0.0**
Minimal Cost-Complexity Pruning:子樹的ccp如果小於設定值，子樹會被裁減。

CCP 算法步驟是對於完全決策樹的每個非葉子節點計算α值，剪掉具有最小α值的子樹，直到剩下根節點，在這一步驟中可得到一系列的剪枝樹；之後用新的剪枝集對上一步驟中的各個剪枝樹進行評估，並找出最佳剪枝樹作爲結果。

Reference:
[決策樹剪枝](https://www.twblogs.net/a/5d3f801ebd9eee51fbf929b4)
[決策樹的剪枝算法](https://www.readfog.com/a/1633934139310837760)

調整參數好文推薦[
機器學習-演算法-細談決策樹分類樹(DecisionTreeClassifier)
](http://www.taroballz.com/2019/05/15/ML_decision_tree_detail/)

Decision Tree 用法 [範例](https://www.datacamp.com/community/tutorials/decision-tree-classification-python)

---

2. 隨機森林(Random Forest)

> **前情提要:** Ensemble Methods 集成學習 : 通過建立幾個模型組合來解決單一預測問題，其工作原理是在數據集上構建多個分類器/模型，各自獨立學習和做出預測，這些預測最後結合成單預測，因此優於任何一個單分類器做出的預。
>
> 多個演算法模型集成成為的模型叫做 **集成評估器(ensemble estimator)**
>
> 組成集成評估器的每個演算法模型都叫 **基評估器(base estimator)**

> 常見的集成演算法分兩類:
> (1)Averagin methods (平均法)-將 多個獨立建構基評估器預測出來的結果平均或是多數決來決定結果。(隨機森林)
> (2)Boosting methods (加速法)- 按順序建構基評估器。前一次的採樣訓練，對於判斷錯誤的樣本，在下一次採樣訓練模型的過程中，會增加其權重，使其更容易被下一個建立的評估器提取到，不斷循環。 (AdaBoost)

> 優劣:
> 平均法: 單獨一個基評估器判斷準確率至少要超過50%，才可以確保集成評估器的表現會比基評估器好;否則集成評估器的效果會劣於基評估器。在使用隨機森林之前，一定要檢查，用來組成隨機森林的分類樹是否都至少有50%的預測正確率。
>
> 加速法: 在一次次建模的過程中，對難以評估特徵的樣本進行強力的預測，構建出一個強評估器。
>
> sklearn中的集成學習方法位於sklearn.ensemble中
>
> Reference:[機器學習-集成學習(ensemble learning)方法概述](http://www.taroballz.com/2019/05/22/ML_Introduction_EnsembleLearning/)

> 基礎觀念: Perturb and Combine Methods
>
> **Perturb**: Create different models.
> 
>
> **Combine**: Create a signle perdiciotn.
> 
>
> Emsemble 缺點就是 無法像單個演算法一樣被解釋
> Reference: [Perturb and Combine Methods](https://www.coursera.org/lecture/machine-learning-sas/perturb-and-combine-methods-b1sgW)
> 也就是說 使用隨機的方式 製造多個分類器，並將每個分類器的結果加以平均。

隨機森林的隨機是什麼:
(1) 每顆樹的建立使用的資料都是從資料集裡面 sample drawn with replacement (bootstrap sample) 重複抽樣。

(2) 節點在分裂時，使用 全部的feature 或是 隨機的subset of (max_features)

使用原因: Decision tree 會存在著 high variance 及 overfitting 的問題。加入以上兩個隨機，可以有效的降低預測的錯誤。隨機森林的特色，就在於 結合不同的樹來減低變異性。

>觀念複習 造成模型不準的原因 Bias vs. Variance
>Bias 偏差-> 模型的預測值與target的誤差
>Variance 變異 -> 模型因為使用的資料不同，預測的結果差異性很大。
>
>參考[從統計學的角度 (Bias and Variance) 來看 Machine Learning Error](https://allen108108.github.io/blog/2019/10/05/%E5%BE%9E%E7%B5%B1%E8%A8%88%E5%AD%B8%E7%9A%84%E8%A7%92%E5%BA%A6%20(Bias%20and%20Variance)%20%E4%BE%86%E7%9C%8B%20Machine%20Learning%20Error/)

模型參數

**n_estimators int, default=100**
裡面會長幾顆樹
> 越大，模型效果往往越好
> .任何模型都有決策邊界，其值達到一定程度時，精確性往往不在上升或開始波動
> .其值越大，計算量與內存消耗量越大，訓練時間越長
> .渴望在訓練難度和模型效果之間取得平衡

**criterion {“gini”, “entropy”}, default=”gini”**
**max_depth int, default=None**
**min_samples_split int or float, default=2**
**min_samples_leaf int or float, default=1**
**min_weight_fraction_leaf float, default=0.0**
**max_features {“auto”, “sqrt”, “log2”}, int or float, default=”auto”**
**max_leaf_nodes int, default=None**
**min_impurity_decrease float, default=0.0**

**bootstrap bool, default=True**
決定資料是否被重複抽樣，如果 False, 則會使用全部的資料去建立一棵樹

**oob_score bool, default=False**
如果使用 bootstrap, 使否使用 oob-> out of bag (重複抽樣) 來做測試。

什麽是袋外樣本oob (Out of bag)：在隨機森林中，m個訓練樣本會通過bootstrap (有放回的隨機抽樣) 的抽樣方式進行T次抽樣，每次抽樣產生樣本數為m的採樣集，進入到並行的T個決策樹中。這樣有放回的抽樣方式會導致有部分訓練集中的樣本未進入決策樹的采樣集中，而這部分未被采集的的樣本就是袋外數據oob。

袋外樣本

而這個袋外數據就可以用來檢測模型的泛化能力(對新鮮樣本的適應能力)，和交叉驗證類似。可以理解成從train datasets 中分出來的validation datasets。

使用 OOB, 就不需要分訓練及測試資料，也不需要交叉驗證。

用法:

from sklearn.ensemble import RandomForestClassifier 
forest = RandomForestClassifier(n_estimators = 100, oob_score = True)

train mode:

forest.fit(X_train, y_train)
print('Score: ', forest.score(X_train, y_train))

Score: 0.979921928817 (訓練model的分數)

print(forest.oob_score_)

0.86453272101 (training set oob 分數)

print('Score: ', forest.score(X_test, y_test))
Score: 0.86517733935
測試集的分數

測試集的分數 和 oob是 相似的

**n_jobs int, default=None**
-1 使用全部的資源運算

**random_state int, RandomState instance or None, default=None**
如果 bootstrap=True, 重複取樣時就會random; 如果 max_feature < n_features，選取特徵時就會隨機選取。

**verbose int, default=0**
數字越大 log 印出來的量就越多

**warm_start bool, default=False**
Ture:將上次訓練完的結果投入下次使用
False:每次都重新訓練

**class_weight{“balanced”, “balanced_subsample”}, dict or list of dicts, default=None**
每個分類的權重

**ccp_alpha non-negative float, default=0.0**
選擇 成本複雜度大於 ccp_alpha 的值來裁剪樹

**max_samples int or float, default=None**
如果 bootstrap(重複取樣)= True，則該值會是重複取樣的數量。

Rerfrence: [Sklearn学习笔记（2）-随机森林 調整參數](https://zhuanlan.zhihu.com/p/138428376)

---

5. XGBoost

前情提要:
在 Emsumble method 裡面，有 stronger learner 和 week learner.

弱學習器就是一個比隨機猜測稍微好那麼一點的模型。如果讓一個模型做有4個選項的選擇題，正確率稍大於25%，比隨機猜測好但也好不了多少，那它就是一個弱學習器。

XGBoost 是 gradient boosting framework. Gradient Boosting 又名為 Additive Training，此方法最初先以常數作為預測，在之後每次預測時新加入一個學習函數 (參數)：

[Reference: 機器學習 — Gradient Boosting (1)](https://medium.com/@gary1346aa/%E6%A9%9F%E6%A2%B0%E5%AD%B8%E7%BF%92-gradient-boosting-1-272e8d7b17e1)

#### 罐罐
##### 支持向量機(SVM)
4. SVM

> **Support Vector Machaine**
> 主要用於二項分類，動作很像是瓜分領土，找到最適合的分界線切一刀，讓交界線到兩邊的距離相同，不會吵架。
> 可以根據你想要怎麼切 (kernel)，來切直線或非線性
> (原理就是你可以把資料映射到更高維度再來一刀切，切完在映射回來)


- 概念：https://medium.com/jameslearningnote/%E8%B3%87%E6%96%99%E5%88%86%E6%9E%90-%E6%A9%9F%E5%99%A8%E5%AD%B8%E7%BF%92-%E7%AC%AC3-4%E8%AC%9B-%E6%94%AF%E6%8F%B4%E5%90%91%E9%87%8F%E6%A9%9F-support-vector-machine-%E4%BB%8B%E7%B4%B9-9c6c6925856b
- 數學： https://zhuanlan.zhihu.com/p/22400898


- 這段大概簡述數學在幹嘛 (怕你看不懂)
- Q: 求分界線及分界線到兩邊的距離 Margin?
- A: 這邊用說的，假設所有點都在二維平面，分界線為直線
- 假設存在分界線 `WT*X+b=0`，正交分界線的向量為 `vW` (`vWT` = `vW` 取正交)
- **`vW` 為 Margin 向量，要求得最大的 Margin 相等於最大的 vW 距離，即可知道分界線**
- 分界線向外擴展，直到接觸兩邊的鄰近點 `X1`, `X2`
- 可得知 `vX1X2` 映射在 `vW` 的距離 = 寬度距離 = 2*Margin
- 所以 Margin = (`vX1X2`) . (`vW` / ||`W`||) / 2
- `vW` / ||`W`|| 為 `vW` 單位向量
- 以上
>由於分界線依賴於 `vW` 距離，而 `vW` 又依賴於邊界上的向量，因此由邊界的向量支持整個分界線，因此稱為支持向量

**說明**
- 超級重要的二項分類法
- 可以媲美機器學習出來的結果
- 在兩群資料中找到最棒的分界線 W
1. 盡可能最大的 margin
2. 線w到兩坨中最短的距離，兩邊等距
- 監督式學習 used for classification, regression and outliers detection.
- 優點
- 切出來的線很漂亮，擁有最大margin的特性
- 可以很容易透過更換Kernel，做出非線性的線
- 可處理高維空間的資料
- 在維度數大於樣本數的情況下仍然有效。
- 具通用性，透過置換 kernel function 達到不同效果
- 缺點
- 效能較不佳，由於時間複雜度為O(n²)當有超過一萬筆資料時，運算速度會慢上許多
- 如果特徵數量遠大於樣本數量，在選擇 kernel function 時避免 over-fitting，正則化項至關重要
- SVM 不直接提供概率估計

**Code**

> https://scikit-learn.org/stable/modules/svm.html
>
> 看這篇說明：https://medium.com/jameslearningnote/資料分析-機器學習-第3-4講-支援向量機-support-vector-machine-介紹-9c6c6925856b

**參數**
主要調節的引數有：C、kernel、degree、gamma、coef0

- C：C-SVC的懲罰引數 C，預設值是1.0
- C是鬆弛係數的懲罰項係數。如果C值設定比較大，那SVC可能會選擇邊際較小的，能夠更好地分類所有訓練點的決策邊界，不過模型的訓練時間也會更長。如果C的設定值較小，那SVC會盡量最大化邊界，決策功能會更簡單，但代價是訓練的準確度。換句話說，C在SVM中的影響就像正則化參數對邏輯迴歸的影響。
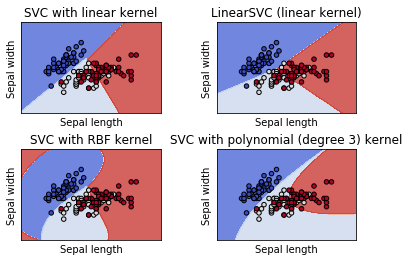
- kernel： 核函式，預設是rbf，可以是 `linear`, `poly`, `rbf`, `sigmoid`, `precomputed`
　　- 0 – `linear` 線性：u'v
　　 - 1 – `poly` 多項式：(gamma*u'*v + coef0)^degree
　　- 2 – `rbf` RBF函式：exp(-gamma|u-v|^2)
　　- 3 – `sigmoid`：tanh(gamma*u'*v + coef0)
　　- 
- degree ：多項式 `poly` 函式的維度，預設是3，選擇其他核函式時會被忽略。
- gamma ： `rbf`, `poly` 和 `sigmoid` 的核函式引數。預設是 `auto`，則會選擇1/n_features
- coef0 ：核函式的常數項。對於 `poly` 和 `sigmoid` 有用。
- probability ：是否採用概率估計？ 預設為False
- shrinking ：是否採用 shrinking heuristic 方法，預設為 True
- tol ：停止訓練的誤差值大小，預設為 1e-3
- cache_size ：核函式 cache 快取大小，預設為200
- class_weight ：類別的權重，字典形式傳遞。設定第幾類的引數 C 為 weight*C (C-SVC中的C)
- verbose ：允許冗餘輸出？
- max_iter ：最大迭代次數。-1為無限制。
- decision_function_shape ：‘ovo’, ‘ovr’ or None, default=None
- random_state ：資料洗牌時的種子值，int值

**同場加映！！！**

**SVM 的子孫們**
> scikit-learn SVM算法庫封裝了libsvm 和 liblinear 的實現，僅僅重寫了算法了接口部分。分爲兩類，分類：SVC， NuSVC，和LinearSVC。迴歸：SVR， NuSVR，和LinearSVR 。
>
> 1. SVC (C-SVC, C-Support Vector Classification)
> 預設使用 RBF 作為 Kernel，
> 由於要用 SVM 做分類，但資料集可能會有不易分割的狀況 (不易分割不代表不能分割，是否能夠分割完整取決於 Kernel )，
> 因此會允許部分容錯空間，而 SVC 採用鬆弛係數來決定採用哪個點作為支持向量。
> (允許容錯空間的 SVC 稱為軟間隔；反之完全線性可分地稱為硬間隔)
>
> > 鬆弛係數 ζ
> > 這是個很麻煩的數學公式，用到對偶函數、拉格朗日函數，但這交給數學家處理，我們認識塗上意義跟重點係數就好。
> > 數學：https://www.twblogs.net/a/5e51a1eabd9eee2117c154c3
> > 
> > 簡單來說，就是原先的 SVC 算出好支持向量 w 之後，今天有一個分類錯誤的點 Xp 出現，就要計算這個點損失函數，
> > 原先的分界線範圍往外平移至 Xp 上，得出新的分界範圍跟新的支持向量 (平移距離則為 ζ，並投影到法向量得出)，
> > `原先的支持向量` 跟 `新的錯誤產生的支持向量`，帶入損失函數進行判斷 (對每個點做估算)，**其中新產生的 ζ 會與 常數 C 相乘**，來表示 ζ 對函示的影響力，最終會決定出要以哪個點作為新的支持向量。
> > C 稱之為逞罰係數，表示錯誤點對鬆弛係數 ζ 的懲罰力度
> >
>
> 2. NuSVC（Nu-Support Vector Classification）
> 與 SVC 相同原理，但他沒有懲罰係數 C，而是用 Nu。
> Nu代表訓練集訓練的錯誤率的上限，或者說支持向量的百分比下限，取值範圍爲(0,1],默認是0.5.它和懲罰係數C類似，都可以控制懲罰的力度。<br/>
> 因此Nu沒有懲罰係數C，因爲它會自己選
> 當模型錯誤率達到 Nu 值後，便會以選擇當下錯誤率低的作為新的支持向量
> 跟 SVC 差別在於，每當新的錯誤產生就必須算一次鬆弛係數，來交叉比對選擇更好的支持向量，但 NuSVC 則是累積達到一定的錯誤率，會自動選適合的點做支持向量。

> 3. LinearSVC（Linear Support Vector Classification）
> Kernel 固定為 Linear 不可以更改，一樣有 C 可以調整，但只限於線性可分割的資料集使用。

**Q: SVM 能夠處理分二類以上的資料嗎？**
> A:可以，把多類資料兩兩一組來看，但怎麼看有分成兩種：OvO (One-v-One), OvR (One-v-Rest)
> 假設資料集有 A, B, C 三類：
> 1. OVR (全天下唯我獨尊):
> 訓練當下的點為一類，其餘為一類，分別做完全部類(三個)的模型，得出(三個)SVM。
> EX: 當模型要算 A 分界線時，會視為 A 與 其他(B,C)
> 要預測未知點時，通通都丟進去，投票最大的為最終結果。
> P.S. 不常用，因為資料可能存在偏差導致。
>
> 2. OVO (彼此手牽手):
> 全部每兩兩一組做一次模型，有三個分類，就會得出 (3+2+1) 個模型。
> EX: 當模型要算 A 分界線時，就會產生 AB, AC, AD 三個 SVM，B 就 BC, BD (BA 已經做過了)
> 要預測未知點時，通通都丟進去，投票最大的為最終結果。

**Q: Kernel Function 是啥？**
> A: 在 SVM 裡，有時候資料集問題，我們無法在原始空間(Rd)中適當的找到一個線性分類器將兩類區隔開，這時後此需要找到一個非線性投影(φ)將資料進行轉換到更高維度的空間，此時在高維度的空間中只需要一個線性分類器/hyperplane就可以完美分類。
> https://youtu.be/3liCbRZPrZA
>
> 但我們又很難直接去設計一個好的非線性投影(φ)公式，因此需要 kernel function 來輔助。(轉換的過程稱為 Kernel Trick)
>
> **Kernel Function 定義**
> 只要對所有的資料，有一個函數可以滿足
> k(x,y)=⟨φ(x),φ(y)⟩
> 這個k(x,y)就是一個kernel函數，⟨a, b⟩表示向量a和b做內積。
>
> 但我們怎麼知道什麼函數可以滿足這個條件，所以有個定理(Mercer’s theorem)說如果有一個函數(φ)存在，這個k必需滿足Mercer’s condition，k就是kernel函數。
> 簡化說就是如果所有的資料帶到這個kernel function中的和必須大於等於 0
>
> **常見的 Kernel Function**
> 
> > d為正整數(通常在call api時，這個部份都會稱為degree)，σ為非0的實數(通常在call api時，這個部份都會稱為gamma)
>
> Linear Kernel:
> - 優點
> - 簡單快速
> - 具解釋性
> - 缺點
> - 資料本身必須要是 Linear Separable
>
> Polynomial Kernel:
> - 優點
> - 資料並不一定要 Linear Separable
> - d 的取值可以從資料的特性來判斷
> - 缺點
> - 太多參數必須做選擇
>
> Gaussian Kernel ( RBF Kernel ):
> - 優點
> - Powerful Kernel
> - K 值通常不會太大
> - 僅一個參數 γ
> - 缺點
> - 解釋性低
> - 計算速度慢
> - Overfitting 的機會很大
>
> Sigmoid Kernel:
> 結合 SVM 與 NN 的概念結合，看這篇： https://hackmd.io/@allen108108/r1ycwIh-H

---

#### Ben
##### 最近鄰居
5. KNN
> 顧名思義, KNN演算法透過找尋距離最近的**K個鄰居(K nearst neighbor)**以及**多數決(majority-volting)**，決定未知資料的種類

* 名稱: **K-nearst neighbor**(K-近鄰演算法)
* 分類: 監督式學習
* 用途: 分類/回歸
* 複雜度: ${O(N)}$
* 特性
* 最簡單的機器學習方法
* 不適用於類別分布不均的資料集
* 不需訓練
* 預測所需的運算量(時間)**正比於**資料集內樣本的數量
* 適合少樣本的數據集
* 不適合大樣本的數據集
* 重要參數
* K
* 距離函數(假定兩資料分別為${x}$, ${y}$, 維度為${n}$)
* 餘弦距離(cosine angular distance)
$${d(x, y)= \frac{x\cdot y}{\lVert x \rVert \times \lVert y \rVert} = \frac{\sum_{i=1}^n(x_i\times y_i)}{\sqrt{\sum_{i=1}^n(x_i)^2}\times\sqrt{\sum_{i=1}^n(y_i)^2}}}$$
* 曼哈頓距離(Manhattan distance)
$${d(x,y)=\sum_{i=1}^n(|x_i-y_i|)}$$
* 歐式距離(Euclidean distance)
$${d(x,y)=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}}$$
* 步驟
1. 決定K(通常為奇數, 若設為偶數, 有可能遇到無法分類的情況)
2. 依序計算所有已知資料與未知資料的距離
3. 多數決確定未知資料類別
* 說明(以二維舉例)
* 已知${m}$筆資料分布(已知代表有標記類別, 以正方形、三角形、圓形表示各種類別)
* 未知資料(以星形表示)
* 計算${1}$筆未知資料與${m}$筆已知資料的距離
* 選取${k}$筆已知資料, 投票決定未知資料的類別
* 當有${n}$個未知之料要計算, 計算量為${n}$倍
* 不平衡的資料所造成的影響
* ${k=1}$時容易overfitting, ${k}$很大時容易underfitting

* scikit-learn
* 基本概念
* KNN的基本概念是去透過計算未知資料與已知資料之間的最短距離, 作為未知資料分類的依據
* k值得選擇有兩種模式
* 使用者自定義的常數(**k-nearest neighbor learning**)
* 該區域點的密度自動調整(**radius-based neighbor learning**)
* 距離函數: 通常可以是任意一種指標, 例如**Euclidean distance**
* 非監督式近鄰演算法
* ```brute-force```: 即暴力法/窮舉法, 若資料集為${N}$筆, 資料維度為${D}$, 則複雜度為${O[DN^2]}$, 此方法將計算資料集中所有點與點間的距離。隨著${Ｎ}$上升, 此方法變得不可行。
* ```KDTree```: 全名為K-dimensional tree, 一種用於高維資料檢索的資料結構, 適用於低維度的資料(${D<20}$)，在低維度的資料運行速度非常快。其概念為若A點距離B點很遠, 而B點距離C點很近, 則不需透過實際計算A點到Ｃ點的距離, 也可知道A點距離C點很遠。
* ```BallTree```: BallTree可以視為```KDTree```的改良版, 雖然此方法的建置過程比較繁瑣, 但適用於高維度的資料。

##### 聚類
6. K-Means
* k-平均算法
* 非監督式學習
* 聚類分析方法
* 優缺點
* 優點
* 計算速度快
* 容易理解
* 缺點
* 需要決定k值
* k值影響分類結果
* 對於某些資料集, 分類效果不好
* 有極值
* 類別間**樣本數量差異過大**
* 非線性的數據
* 起始點的選擇, 導致得到不同的解，得到的解可能為**local optimum**(局部最佳解), 而非**global optimum**(全域最佳解), 因此得到一解後必須再重複執行數次以確保得到**global optimum**
* ```k-means```與```knn```沒有任何關聯
* 步驟
1. 假設資料分布如下圖, 且決定k=3
2. **隨機**選取3個(k=3)起始點, **作為每個類別的中心點**
3. 分別計算第一個點到三個類別中心點的距離
4. 將第${1}$個點分類為距離最近類別
5. 對第${2}$個點做相同動作
6. 對第${3}$個點做相同動作
7. 直到做完所有的點
8. 找出所有類別在該次迭代的中心(即平均值)
9. 重複步驟${3}$至步驟${8}$, 直到所有點被分類
**. . . . . .**
10. 計算**total variation**
11. 重新選起起始點再做一次
13. 這次的分類結果不同
14. 中心點的位置也不同
15. 重複計算每個點到中心的距離
16. 直到分類不再改變
17. 計算**total variation**
18. 演算法根據使用者設定的迭代次數不斷重複,並保留最佳的結果
* 如何決定k
* ${k=1}$
* ${k=2}$
* ${k=3}$
* ${k=4}$
* ${k}$與**total variance**

* <a href=https://www.naftaliharris.com/blog/visualizing-k-means-clustering/>k-means 體驗</a>

#### 若安

##### 線性
7. Linear Regression (線性迴歸)：用來預測一個連續的值，目標是想找一條直線可以逼近真實的資料。
* 原理：通過一個或多個自變量與因變量進行建模的迴歸分析。
- 當一個的自變數(X)情況的叫做 單變量線性迴歸(簡單線性回歸)Simple Linear Regression。
- 當有兩個以上的自變數(X)情況的叫做 多變量線性迴歸 (多元線性迴歸) Multivariable Linear Regression。

> **多項式迴歸 Polynomial regression**：
> 當自變量X 和因變量 y 之間的關係被建模為關於 x 的 n 次多項式，x的值與 y 的相應條件均值之間的非線性關係。須注意當加入多個高度相關的變數，進行多項式回歸，會導致「**多重共線性(multicollinearity)**」
- 選擇自變數的方法，避免多重共線性
- 確認性的指定
以理論或文獻上的理由為基礎，研究人員可以指定哪些變數可以納入迴歸方
程式中，但必須注意的是，研究人員必須能確認選定的變數可以在簡潔的模
式下，達到最大量的解釋。
- 順序搜尋法(Sequential Search Methods)
順序搜尋法是依變數解釋力的大小，選擇變數進入迴歸方程式，常見的有向
前增加 (Forward Addition)、往後刪除 (Backward Elimination)、逐次估計
(Stepwise Estimation) 三種，我們分別介紹如下：
1. y 向前增加(Forward Addition)：自變數的選取是以達到統計顯著水準的變
數，依解釋力的大小，依次選取進入迴歸方程式中，以逐步增加的方式，
完成選取的動作。
2. y往後刪除(Backward Elimination)：先將所有變數納入迴歸方程式中求出
一個迴歸模式，接著，逐步將最小解釋力的變數刪除，直到所有未達顯
著的自變數都刪除為止。
3. y 逐次估計(Stepwise Estimation)：逐次估計是結合向前增加法和往後刪除
法的方式，首先，逐步估計會選取自變數中與應變數相關最大者，接著，
選取剩下的自變數中，部份相關係數與應變數較高者 (解釋力較大者)，
每新增一個自變數，就利用往後刪除法檢驗迴歸方程式中，是否有需要
刪除的變數，透過向前增加，選取變數，往後刪除進行檢驗，直到所有
選取的變數都達顯著水準為止，就會得到迴歸的最佳模式。

> **穩健迴歸Robust regression**：
> 由於線性回歸方程式，很容易受到資料中的離群值影響判斷，因此發展可以用[RANSAC (RANdom SAmple Consensus)隨機抽樣一致法](https://iter01.com/511426.html)，反覆隨機擷取資料迴歸分析，計算正常值的資料比例，以正常值最高的直線作為迴歸直線

> 

* 分類：監督式學習
* 公式：
y 是因變量（y）對自變量（x）任何給定值的預測值
B0 是截距，即 x 為 0 時 y 的預測值
B1 是回歸係數–表示期望 y 隨著 x 的增加而改變多少
x1、x2 是兩個以上的自變量
e 是估計值的誤差
* 

* 線性迴歸需要滿足四項基本統計假設：
1. 線性關係：依變項(Y)和自變項(X)必須是線性關係。
2. 殘差值的分配具有「常態性(Normality)」：若母體為常態分布，殘差值也為常態。
3. 殘差值的分配具有「獨立性(Independency)」：自變項(X)的殘差值，應為互相獨立的。
4. 變異數同質性(Constant Variance)： 變異數若不相等會導致自變項(X)無法有效估計依變項(Y)
* [sklearn](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html)
`class sklearn.linear_model.LinearRegression(*, fit_intercept=True, normalize='deprecated', copy_X=True, n_jobs=None, positive=False)`
* 步驟：
1. 導入數據
2. 將數據拆成訓練集、測試集
3. 訓練線性回歸模型
4. 算出截距值(Interception)、係數值(Coeficient)、模型準確度(Score)
5. 拿訓練好的模型去預測測試資料集的Y
* 參數(Parameters)
* fitintercept (bool值)：
預設為True，表示有將y軸的截距加入 ，並自動計算出最佳的截距值，如果"False"，迴歸模型線會直接通過原點
* normalize(bool值) 是否將數據做標準化（Normalize），預設為False
* copy_X : 預設為True，表示X會被Copied
* n_jobs : 計算模型所使使用的CPU數量，預設為1，如果傳入-1，就會使用全部的CPU*
* 屬性(Attributes)
* coef_ : 訓練完後，模型的係數，如果有多個目標值，也就是多個y值，就會回傳一個2Darray，裝載所有的係數值
* predict : 預測數據
* score : 評估或準確度（Accuracy），它會利用R平方來判斷我們訓練出來模型的預測精準度，也就是預測的準確度

* 線性回歸的評估指標
* MSE(Mean Square Error)平均平方誤差(均方差)：把所有誤差求平方後，求其平均，對異常值非常敏感,因為差值是一個正平方形,對異常值的重要性更高。該行為是一條二次曲線,特別適用於梯度下降算法,接近最小值時梯度會更小。

* MAE(Mean Absolute Error)絕對平均誤差：所有誤差求絕對值後，求其平均，每個點的梯度都是相同的,即使值接近最小值(可能會產生跳躍)。它需要動態修改學習率以減少接近最小值的步長。

* R2(R-square)R平方、決定係數：將預測誤差正規化所得到的指標，且評估模型是否具有解釋性，完全無法預測為0，全部能夠預測時為1，數值越大越好。

殘差(Residual)：y預測值與y實際值之間的差值
誤差(Error)：y觀察值與實際值之間的差值

* 偏差（bias) vs. 方差（variance)
> 在模型預測中，模型可能出現的誤差來自兩個主要來源：
> 1、因模型無法表示基本數據的複雜度而造成的偏差（bias);
> 2、因模型對訓練它所用的有限數據過度敏感而造成的方差（variance)。
> 誤差是測量值與真實值之間的差值。
> 用誤差衡量測量結果的準確度，用偏差衡量測試結果的精確度；
> 誤差是以真實值為標準，偏差是以多次測量結果的平均值為標準。
> 而方差在統計學中是指各個數據與其平均數之差的平方的和的平均數，
> 它表示的是一種偏離程度：當數據分佈比較分散時，方差就較大；
> 因此方差越大，數據的波動越大；方差越小，數據的波動就越小。
> 白話文：
> 以打靶作為舉例，
> 如果說你打靶打得很精 "準"，意味你子彈射中的地方離靶心很近，即 Low Bias；
> 如果說你打靶打得很精 "確"，意味你在發射數槍之後這幾槍彼此之間在靶上的距離很近，即
>
> Low Variance
> 
> Bias-Variance Tradeoff：
> 透過權衡 Bias Error 跟 Variance Error 來使得總誤差( Total Error ) 達到最小。
> 

* 在線性迴歸中，抑制迴歸過度擬合
* [導入懲罰項(正規化項)](https://www.geeksforgeeks.org/lasso-vs-ridge-vs-elastic-net-ml/)
[Ridge vs Lasso Regression, Visualized!](https://www.youtube.com/watch?v=Xm2C_gTAl8c)
* L1正規化的迴歸稱為套索迴歸(Lasso Regression)：以迴歸係數的**絕對值和**作為基準

* L2正規化的迴歸稱為嶺迴歸(Ridge Regression)：以迴歸係數的**平方和**作為基準

* 同時使用L1、L2正規化的迴歸稱為彈性網絡(Elastic Net regression)

8. Logistic Regression(LR)：估計模式中每一個自變數的勝算比(Odds)。
>前情提要：
>線性回歸 vs. 邏輯斯回歸
>(簡單)線性回歸目的是要找一條方程式能夠最接近真實的資料集。
>(簡單)邏輯斯回歸目的則是要找到一條方程式可以將兩類的資料群進行分類。
>

* 原理：

1. Net input function(淨輸入函數)：線性回歸中，我們會計算權重與輸入的線性組合
2. Sigmoid function(乙狀函數)：
4. threshold function(定限函數)：指僅有二值的交換函數。其引數可能不只一個，且須為布林引數，若引數之特定數學函數值大於定限，則對應函數之值為1，否則為0。
**白話文：只要計算出來的值高於閾值就輸出1，否則就是0**
> Perceptron是根據 w0*x0+w1*x1+…+wn*xn >0 或≤0來判斷成A或B類。
<!--  -->
>Logistic Regression是一個平滑的曲線，當w0x0+w1x1+…+wnxn越大時判斷成A類的機率越大，越小時判斷成A類的機率越小。

* 分類：監督式學習
* 優點：非常有效率、不需要大量運算資源
* 缺點：不能用於解決非線性問題
* 勝算(Odds)：
p的值介於0~1之間，p接近0時表示Y成功的機會很小，接近1時則表示成功的機會很大
* 舉例：

| | 幾次是硬幣為正面 | 幾次是硬幣為反面 | 總共擲幾次 |
| ---- | ---------------- | ---------------- | ---------- |
| 小花 | 10 | 10 | 20 |
| 小明 | 2 | 18 | 20 |
| 小美 | 12 | 8 | 20 |
| 小林 | 6 | 14 | 20 |

勝算(Odds)：
小花 exp(10/10) = exp(1)=2.71828183
小明 exp(2/18)= exp(0.111)
小美 exp(9/11)=exp(0.8181)
小林 exp(6/14) = exp(0.4285)
* 對勝算值(Odds)取自然對數：

* 當 Δ odds > 1，表示當Xi 增加時，事件Y 發生的勝算會提高
* 當 Δ odds < 1，表示當Xi 增加時，事件Y 發生的勝算會降低

* 分類問題在參數型學習(parameter learning)通常都是用[最大概似函數估計法]
* 二元交叉熵
* (https://wangcc.me/LSHTMlearningnote/likelihood-definition.html) (Maximum Likelihood Estimation, MLE)求解

* [Sklearn](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html)

    def LogisticRegression(penalty='l2',
        dual=False,tol=1e-,C=1.0,fit_intercept=True,
        intercept_scaling=1,class_weight=None,
        random_state=None,solver='liblinear',
        max_iter=100,multi_class='warn',
        verbose=0,                   
        warm_start=False,n_jobs=None,l1_ratio=None)

參數：
1. penalty：正則化類型選擇，預設為"L2",可選擇"L1"，"L2"，"elasticnet"和"None"。
2. solver： 對邏輯斯回歸"損失函數優化"的方法，預設為”liblinear”，可選”newton-cg”,”lbfgs”,”liblinear”,”sag”,”saga"。
* liblinear：
使用了開源的liblinear庫實現，內部使用了坐標軸下降法(coordinate descent)來迭代優化損失函數。
* lbfgs：
擬牛頓法的一種，利用損失函數二階導數矩陣即海森矩陣(Hessian matrix)來迭代優化損失函數。
* newton-cg：
也是牛頓法家族的一種，利用損失函數二階導數矩陣即海森矩陣來迭代優化損失函數。
* sag：
即隨機平均梯度下降，是梯度下降法的變種，和普通梯度下降法的區別是每次迭代僅僅用一部分的樣本來計算梯度，適合於樣本數據多的時候。
* saga：
優化、無偏估計的sag方法。(大於10萬的數據，那麼選擇”sag”和”saga”會讓訓練速度更快。)

| 正則化 | 演算法 | 適用場景 |
| ------ | ------------------- | -------------------------------------------------- |
| L1 | liblinear | liblinear適用於小數據集。如果選擇L2正則化發現還是過擬合(Ovetfitting)，即預測效果差的時候，就可以考慮L1正則化。而如果模型的特徵非常多，希望一些不重要的特徵係數歸零，從而降低模型複雜度的話，也可以使用L1正則化。 |
| L2 | liblinear | libniear只支援多元邏輯回歸的OvR，不支援MvM，但MVM相對精確。 |
| L2 | lbfgs/newton-cg/sag | 較大數據集，支援one-vs-rest（OvR）和many-vs-many（MvM）兩種多元邏輯回歸。 |
| L2 | sag | 如果樣本量非常大，比如大於10萬，sag是第一選擇;但不能用於L1正則化。 |

3. dual：對偶或者原始方法，布爾類型，預設為False。
4. tol：停止迭代求解的閾值，單精度類型，預設為1e-4。
5. C：正則化係數的倒數，必須為正的浮點數，預設為 1.0，這個值越小，說明正則化效果越強。換句話說，這個值越小，越訓練的模型更泛化，但也更容易欠擬合。
6. fit_intercept：預設為True，表示有將y軸的截距加入 ，並自動計算出最佳的截距值，如果"False"，迴歸模型線會直接通過原點
7. intercept_scaling：預設為 1.0，特徵向量添加一個常量。
8. class_weight：分類權重，預設為None，可選擇"balanced"、None、自行輸入dict類型(class_weight={0:0.9, 1:0.1})。
9. random_state：設置隨機數種子，可以是int類型和None，默認是None。當"solver"參數為"sag"和"liblinear"的時候生效。
10. verbose：輸出詳細過程，int類型，默認為0（不輸出）。當大於等於1時，輸出訓練的詳細過程。僅當"solvers"參數設置為"liblinear"和"lbfgs"時有效。
11. warm_start：設置熱啟動，布爾類型，默認為False。若設置為True，則以上一次fit的結果作為此次的初始化，如果"solver"參數為"liblinear"時無效。
12. max_iter：最大迭代次數，int類型，默認-1（即無限制）。注意前面也有一個tol迭代限制，但這個max_iter的優先級是比它高的，也就如果限制了這個參數，那是不會去管tol這個參數的。

#### Abby
##### 降維
9. Principal Component Analysis（PCA）
* 名稱：主成分分析
* 分類：非監督式學習
* 用途：降低資料維度
* 原理：如何從資料中找尋所對應的直線，讓資料維度下降
* 透過點投影的方式
$$如上圖，預計算出\vec{v}，將{xi}投影至\vec{v}（為藍色向量），透過角度{\theta}與投影向量計算可公式如下$$
$$其中\vec{v}為單位向量，\begin{Vmatrix}v \end{Vmatrix}=1，再透過{cos\theta}計算後如下$$

* 假設資料有六個點，有兩個投影向量v跟v'
> PCA的假設前提是在投影誤差最小的情況下，期望投影後的資料變異最大（最佳直線）

可以看到v向量有比較大的變異量
* 變異量的算法
* 單變量

* 多變量
$${c}是共變異數矩陣(covariance matrix)$$
最大化的變異量為

把限制是改寫後為

偏微分找解

最終

解出來的eigenvalue是變異數和eigenvector最大變化量

* 應用：
* 目的：
* 將資料「化繁為簡」，將原本高維的資料（N 維）重新以一個相較低維的形式表達（K 維，且 K<N）。理想上只要 K 維的表徵（representation）具有代表性，就能夠表現出原來 N 維資料的大部分特性，**用簡潔的方式呈現該組資料，進而對其本質有更深的理解**。
* 可以避免維度詛咒（curse of dimensionality）
> 維度詛咒（curse of dimensionality）
> 預測能力會隨著維度數(變數)增加而上升，但當模型樣本數沒有繼續增加的情況下，預測能力增加到一定程度之後，預測能力會隨著維度的繼續增加而減小
* 實例：各種資料須要降低複雜度與維度的時候,都可以使用
* SOP：
* 數據正規化
$${(x_{i}-mu)\over std}$$
* 計算方差
* 解eigenvalue和eigenvector
* 限制：
* PCA會導致在沒有或低特徵相關性或不滿足線性假設的數據集上的模型性能下降
* 分類準確性：投影後計算的方差不考慮類的區分特徵，因此區分一個類與另一個類的信息可能在低方差分量中並且可能被丟棄
* 可解釋性：每個主成分是原始特徵的組合，比較難解釋單特徵對資料的含意。
* code
[sklearn](https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html)

    from sklearn.decomposition import PCA
    pca = PCA(n_components=int, whiten=False, svd_solver='auto')
    pca.fit(X)
    ###
    # n_components：要保留維度數
    # whiten：對降維後的數據的每個特徵進行正規化{True, False}
    # svd_solver：分解SVD的方法{auto, full, arpack, randomized} 
    # -randomized一般適用於數據量大
    # -full使用一般矩陣
    # -randomized使用scikit-learn計算
    # -arpack使用scipy庫的sparse計算
    # -auto：PCA自己去衡量
    # explained_variance_：降維後的各主成分的方差值
    # explained_variance_ratio_：降維後的各主成分的方差值占總方差值的比例(比例越大，則越重要)
    ###

##### 梯度下降
10. 準確率梯度下降法(SGD)
* 原理：
* 分類：非監督式學習
* 應用：

#### Michael
##### 高斯程序
11. Gaussian Process
* 原理：
- Gaussian Process(高斯過程)為觀測連續域的隨機過程(Random Process),在高斯過程中每個點都是與一個常態分佈的隨機變量相關聯
- 其為惰性學習,且為一個無參數的方式
- 利用點與點之間的同性質度量作為核函數,構造協方差函數,通過訓練樣本得到聯合機率密度,進而求得新數據預測值
- 要預測新數據點的y值，從概率的視角看，我們可以用條件概率來預測，即在歷史數據的X、Y值條件下，當前y的概率分布。
- 我們當然對條件概率p（y* | y）更感興趣："給定數據，y *的特定預測的概率有多大？"。 這個條件概率仍然遵循高斯分布（推導過程略），所以有：
- 我們對y*的最佳估計是這種分布的平均值：
- 我們估計的不確定性由方差給出：
* 分類：監督式學習
* 應用：觀測趨勢得到適合的預測值
* 範例：

    >>> from sklearn.datasets import make_friedman2
    >>> from sklearn.gaussian_process import GaussianProcessRegressor
    >>> from sklearn.gaussian_process.kernels import DotProduct, WhiteKernel
    >>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0)
    >>> kernel = DotProduct() + WhiteKernel()
    >>> gpr = GaussianProcessRegressor(kernel=kernel,random_state=0).fit(X, y)
    >>> gpr.score(X, y)
    0.3680...
    >>> gpr.predict(X[:2,:], return_std=True)
    (array([653.0..., 592.1...]), array([316.6..., 316.6...]))

    >>> from sklearn.datasets import load_iris
    >>> from sklearn.gaussian_process import GaussianProcessClassifier
    >>> from sklearn.gaussian_process.kernels import RBF
    >>> X, y = load_iris(return_X_y=True)
    >>> kernel = 1.0 * RBF(1.0)
    >>> gpc = GaussianProcessClassifier(kernel=kernel,random_state=0).fit(X, y)
    >>> gpc.score(X, y)
    0.9866...
    >>> gpc.predict_proba(X[:2,:])
    array([[0.83548752, 0.03228706, 0.13222543],
       [0.79064206, 0.06525643, 0.14410151]])

* 參考:
https://zh.wikipedia.org/wiki/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83
https://www.zhihu.com/question/46631426

##### 集成方法
12. Ensemble Methods
* 原理：
- Boosting->錯中學
- Bagging->同時學並投票決定
1. 找到誤差互相獨立的基分類器(EX:DT)
2. 訓練基分類器
3. 合併基分類器結果(Volting, Stacking)
* 分類：監督式學習
* 應用：
- RandomForiest
- XGBoost
13. AdaBoost
* 原理：
1. ID3決策樹當基分類器
2. 訓練基分類器
3. 合併基分類器(正確的樣本權重降低以降低錯誤率)
* 分類：
* 應用：

#### 深度學習
#### Ben
1. 卷積神經網路(CNN)
2. 迴圈神經穩路(RNN)
#### Michael
3. 長短期記憶網路(LSTM)
* Z為要存到cell裡面的input
* Zi為操控input gate的訊號（是一個數值）
* Zf為操控forget gate的訊號（是一個數值）
* Zo為操控output gate的訊號（是一個數值）
* a為最後的output
* f(Zi)、f(Zf)和f(Zo)所通過的activation function f 通常會選擇「sigmoid function」. 因為sigmoid function的值是介在0到1之間，而這個0到1之間的值代表了這個gate被打開的程度。若這個activation function的output是1，就代表這個gate是被打開的狀態。
* [ f(Zi) ] input gate
控制g(Z)可不可以輸入的一個關卡。因為假設f(Zi)=0，那g(Z)f(Zi)=0，就好像是沒有輸入一樣；如果g(Z)f(Zi)=1，就等於是直接把g(Z)當作輸入。
* [ f(Zf) ] forget gate
決定要不要把存在memory裡面的值洗掉。
假設f(Zf)=1，也就是forget gate是被開啟的時候，這時原本存在memory cell裡面的c就會直接通過，等於是把之前存的值繼續記得。
forget gate它的開關跟我們直覺的想法是相反的。它被開啟的時候，代表是「記得」；它被關閉的時候，代表的是「遺忘」。
* [ f(Zo) ] output gate
如果f(Zo)=1，就等於h(c’)可以通過output gate，輸出結果。
如果f(Zo)=0，就等於output會變成0，就代表說存在memory裡面的值沒有辦法通過output gate被讀取出來。
1. Many to One:
就是多個時間點來預測下一個時間點 (Ex: 輸入: 一週股價，輸出: 下週一股價)

2. Many to Many:
多個具關聯的資料來預測下一個時間性或者下一個具關聯的資料 (Ex: 輸入: 英文句子，輸出: 中文句子)

#### 罐罐
4. 生成對抗網路(GAN)

> **Generative Adversarial Network**
> 看名字來說，要拆成 **生成 Generative** 與 **對抗 Adversarial** 兩組模型來形成的大模型網路。
>
> 講個小故事：
> 從前從前有個窮鬼畫師，專門模仿名畫來自己做偽畫，但他完全沒有經驗，所以他得要從頭開始學習模仿技巧。
> 每當畫師畫出新的畫時，都會拿去給一起合作的鑑定師去鑑定，鑑定師就會拿原畫跟新的畫作比對，不滿意就告訴畫師一些建議並要求重新畫一張，直到滿意之後才能夠出貨賣給其他人。
> 但是很不幸的事，鑑定師跟畫師都很窮又沒技術，鑑定師也是得從頭學習鑑定技巧。
> 究竟兩個臭皮匠能不能做出栩栩如生的仿畫呢？


**說明**

- 非監督式學習
- 2016年的一個研討會上，楊立昆 (人工智慧研究先驅，也是 Facebook 的人工智慧研究主管) 稱生成式對抗網絡為「機器學習這二十年來最酷的想法」
- 一堆時事新聞
- 擊敗 AlphaGO 的 AlphaGO Master, AlphaGO Zero
-

### L113 機器學習基礎數學
#### 微積分
#### 線性代數
https://codingnote.cc/zh-tw/p/253165/
#### 機率
1. 貝式定理

2. 機率函數
2.1 (PMF)機率質量函數[離散]
2.2 (PDF)機率密度函數[連續]
2.3 (CDF)累積分布函數

3. 先驗與後驗
3.1 先驗機率:
事情還沒有發生，要求這件事情發生的可能性的大小
3.2 後驗機率(條件機率):
事情已經發生，要求這件事情發生的原因是由某個因素引起的可能性的大小

4. MLE與MAP
4.1 (MLE)(Max)最大似然估計
似然函數(likelihood function)是一種在參數θ下觀察到樣本出現的條件機率

4.2 (MAP)最大後驗機率
最大後驗機率（MAP）估計來源於貝葉斯統計學，其估計值是後驗機率分佈（posterior distribution）的眾數。最大後驗機率估計可以對實驗數據中無法直接觀察到的量提供一個點估計（point estimate）。它與最大似然估計有密切的聯繫，但它通過考慮被估計量的先驗機率分佈（prior distribution）使用了增廣的優化目標，因此，最大後驗機率估計可以看作是規則化（regularization）的最大似然估計。

最大後驗概率估計的準確定義如下：

---

## L12

### L121 機器學習資料處理
Extract-Transform-Load
抽取（extract）、轉置（transform）、載入（load）

### L122 機器學習資料分析

### L123 機器學習建模與參數調校