# Why and How zk-SNARK Works
###### tags: `NCKU`

Public Date: March, 2020
Author: Maksym Petkus
Jornal: arxiv e-print archive, cornell university
Speaker: Kuang Chen, Ma

---

## Outline
- ### Abstract
- Zero Knowledge Proof
- ZK-SNARKS and the medium of proof
- ### Introduction (Next time)
- Non-Interactive Zero-Knowledge of a Polynomial
- Obscure Evaluation
- ### Conclusion (Next time)

---

## Zero Knowledge Proof Usage

1. Evidence of Statement Regarding Privacy Data
* Match DNA without exposing all DNA data
* User can do KYC without exposing data
2. Anonymous authentication
* Proof that user's has access to restricted areas
without revealing identity
3. Anonymous payment
* Pay taxes without disclosing income
4. Outsourced computing
* Outsource expensive computation and verify that the
result is correct without re-executing it

---

# ZKP Definition
In any "zero-knowledge proof" system, has two parties

* prover: wants to convince the verifier that some statement is true without revealing data
* verifier: Verify prover knows data

The agreement should satisfy the following three properties:

1. Completeness
1. Reliability
1. Zero knowledge

---

# ZK-SNARKS and the medium of proof
* zk-snarks definition:
* Zero knowledge
* Succinctness
* Non-interactivity
* Arguments
* of knowledge

* The medium of proof
* 

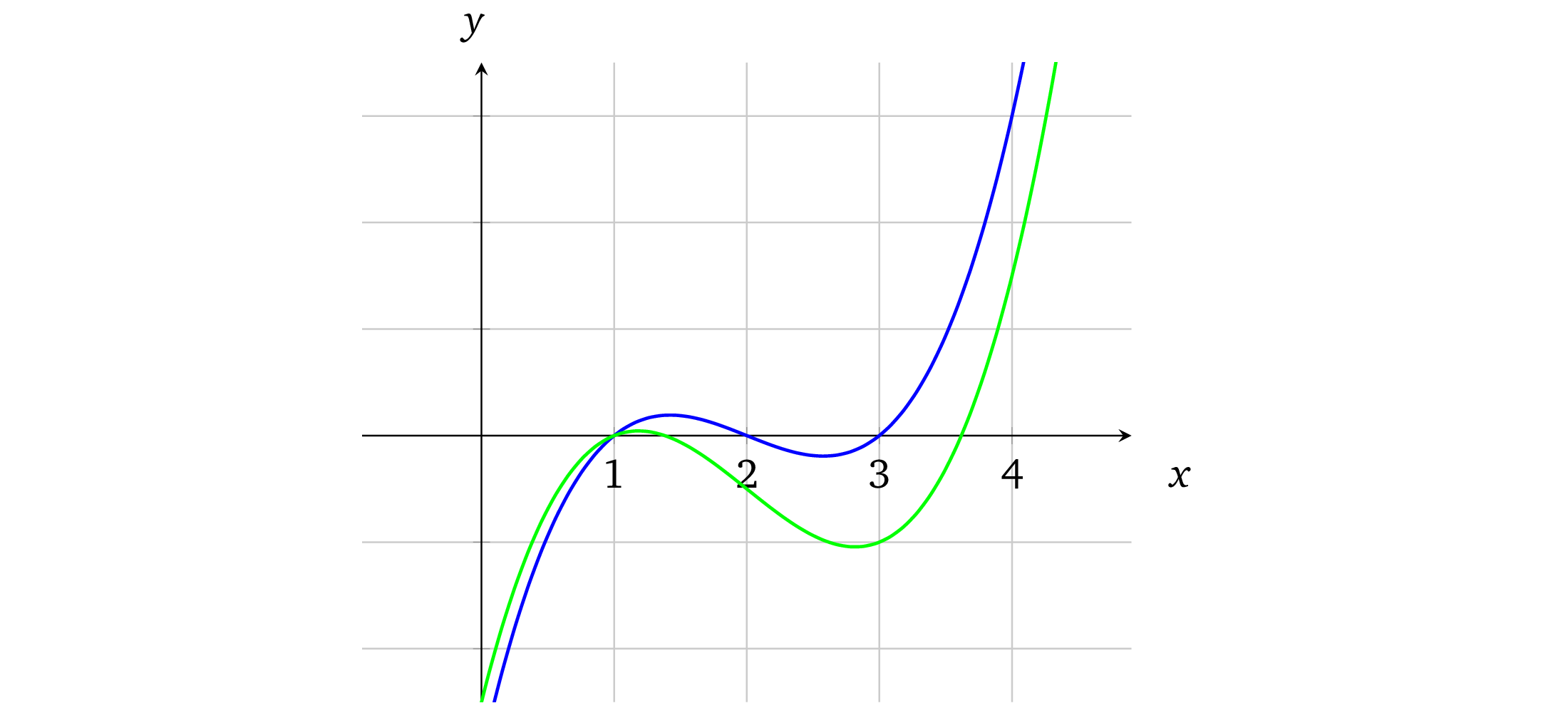
f(x) = x³ – 6x² +11x– 6
d(x) = x³ – 6x² + 10x– 5

If we let f(x) = d(x)

x³ – 6x² + 11x – 6 =x³ – 6x² + 10x – 5
x - 1 = 0

Only x = 1 can fill above equation

---

* The medium of proof

That's why if a prover claims to know some polynomial that the verifier also knows (regardless of the degree of the polynomial) Then they can follow a simple protocol to verify:

Note right of Bob: E(x)
Bob->Alice: gives the x value to the prover
Note left of Alice: P(x)
Alice->Bob: gives the calculation result
Note right of Bob: E(x)/P(x) = 0 (mod x)

Bob: verifier
Alice: prover
E(x): chooses a random value x and computes 
      the polynomial result locally

E(x)%P(x) = 0 : checks whether the local calculation result 
                       and the prover's calculation result are equal

---

If we set x in 1 to 10⁷⁷
* number of points with different calculation results = 10⁷⁷ – d (d: degree)
* hit rate = $\frac{d}{10^{77}}$ (could be considered almost impossible)

**This is why polynomials are a relatively central part of zk-SNARKs even though other proof media may exist.**

---
# Non-Interactive Zero-Knowledge of a Polynomial

## Proving Knowledge of a Polynomial
A polynomial can be expressed in the form (where n is the degree of the polynomial):
$c_nx^n + ... ... + c_1x^1 + c_0x^0$

If one stated that he knows a polynomial of degree 1 (i.e., $c_1x^1 + c_0 = 0$), that means that what one really knows is the coefficients $c_0, c_1$. ($c_n$ can have any value, including 0)

Let us say that the prover claims to know a degree 3 polynomial, such that x = 1 and x = 2 are two of all possible solutions. One of such valid polynomials is $x^3 - 3x^2 + 2x = 0$.
For x = 1: 1−3+2=0.
For x=2: 8−12+4=0.

> This means that the "knowledge" of the polynomial is the coefficients of the polynomial. The so-called "know" polynomial means "know" the coefficients of the polynomial.

---

## Factorization

Any valid polynomial can be as the product of its factors:

$(x - a_0)(x - a_1)...(x - a_n) = 0$

Any $a_s$ are all polynomial solutions. e.g. x for 0, 1, 2

$x^3 - 3x^2 + 2x = (x-0)(x-1)(x-2)$

Prover wants to prove that he knows a certain polynomial without revealing the polynomial, he can use this form to prove

$p(x) = t(x) \times h(x)$

p(x) : Prover's polynomial
t(x) : (x- 1)(x- 2) (also called the target polynomial)
h(x) : Arbitrary polynomial  (that is, x - 0 in our example)

$h(x) = \frac{p(x)}{t(x)}$

If a prover cannot find such a h(x) which means that p(x) does not contain the factor t(x), then the polynomial division will have a remainder

E.g.
$p(x) = x^3 - 3x^2 + 2x$
$t(x) = (x-1)(x-2)=x^2-3x+2$

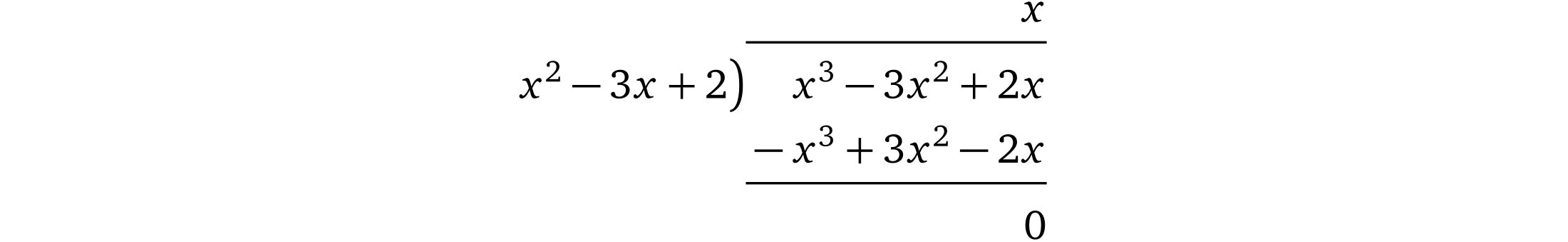
Then we can see that the result h(x) = x, there is no remainder.

Using our polynomial identity check protocol
we can compare polynomials $p(x)$ and $t(x)·h(x)$:

Note right of Bob: t = t(r)
Bob->Alice: gives r to the prover
Note left of Alice: h(x) = p(x)/t(x)
Note left of Alice: evaluates p(r) and h(r)
Alice->Bob: provide p,h to the verifier
Note right of Bob: check p = t · h

Bob: verifier
Alice: prover
t = t(r): samples a random value r, calculates t = t(r) 
p: p(r)
h: h(r)
check p = t * h, if so those polynomials are equal, meaning that p(x) 
has t(x) as a cofactor.


We will get $2x+3$ with the remainder $7x−6$, i.e.: $p(x) = t(x)×(2x+3)+7x−6$. This means that the prover will have to divide the remainder by the $t(r)$ in order to evaluate

$h(x) = 2x + 3 + \frac{7x-6}{t(x)}$

However, since x is randomly chosen by the verifier, there is an extremely low probability that the remainder 7x – 6 will eventually be divisible by t(x).

Now we can verify polynomials based on certain properties without knowing the polynomial, which has given us some properties of zero knowledge and simplicity. However, there are still many problems in this structure:

* The prover may not know the $p(x)$ he claims
* guest $t = t(r)$
* choosing a random value $h$
* $p = t⋅h$
* Because the equation is established, it can also pass the verification of the verifier
* Because the prover knows the random point $x = r$ he can construct an arbitrary polynomial that has something in common with $t(r) ⋅ h(r)$ at $r$
* In the original statement, prover claims to know a polynomial of a particular degree, in the current protocol there is no enforcement of degree. Hence prover can cheat by using a polynomial of higher degree which also satisfies the cofactors check.