# 淺談計算機基本概念
作者 : [邱柏鈞](https://github.com/pjchiou)
---
一段極為簡單的程式碼,就可以讓人出錯。
```c=1
#include <stdlib.h>
#include <stdio.h>
int main()
{
unsigned int a=0;
if (a > -1)
printf("true\n");
else
printf("false\n");
return(0);
}
```
這段程式碼在 linux 下以 gcc 編譯後執行的結果為
:::success
false
:::
初學程式時遇到的 bug 通常僅僅是語法上的不熟悉、或著程式邏輯有誤。這類型的 bug 較為容易解決,編譯器就能夠直接擋下來,甚至有靜態分析工具可以在執行之前就發現 memory leak 。
有一點經驗以後,遇到一些 bug 不見得每次執行都會出現,可能執行數十次才會出現一次(例如 alignment),這類型的 bug 非常難解、難以重現,這時候只能仰賴對基礎概念的了解,充分掌握程式的行為,才有辦法除錯,更進一步寫出安全、可讀、利他、優雅的程式碼。
近年來許多程式語言的語法越來越複雜,也提供許多樣板、工具,使得開發程式的門檻下降許多,接觸了其他高階程式語言後,可能會覺得 C 語言實在是很討厭。閱讀高手的程式碼時連變數宣告都看不懂、涉及指標的操作很容易引發 Segmentation fault、許多的 Undefined Behavior...等等,除此之外,也可能因為切換平台時出現不一樣的行為。
C 語言並非一無可取,否則不可能如此歷久不衰,C 語言出現的目的是開發 UNIX 系統,其許多行為都與底層十分接近,C 語言被稱為最接近底層的程式語言,甚至有人以 "What you see is all you get" 來形容其轉換為組合語言時,常常可以直接對應。
高階程式語言通常有其各自適合的應用。時間有限,我們不可能精通每一種工具,況且許多高階語言改版飛快,以 [C++](https://zh.wikipedia.org/wiki/C%2B%2B) 為例,從 1998 年至今 20 年間有超過15次的改版、擴充。理解其背後的原理,比起持續追逐重要得多。因此本篇內容皆以 C 語言出發,探討計算機系統的行為。
---
## 主題
- 數值系統
- 指標
- macro 與 function
- 最佳化
---
## 數值系統
大部分的系統都為==二補數系統==,看似簡單的二補數系統其實大有學問。在最近知名的一本書 Computer Systems A Programmer's Perspective 3/e (CSAPP) 中的第二章,花了將近 90 頁的篇幅在介紹數值系統。不了解數值系統的情況下所產生的 bug 往往難以發現。
某些程式語言會直接規定常見的資料型別用幾個 bit 來表示,例如 Java 的 int 就是 32 bit,==但 C 語言沒有這樣的規定==。 C 語言的 int 可以是 16 bit 也可以是 32 bit ,只有定義最小必須是多少,一切都定義在 <limits.h> 與 <float.h> 內。
常見的幾組資料模型有以下:
|type|LP32|ILP32|LP64|ILP64|
|:-:|:-:|:-:|:-:|:-:|:-:|
|char|8|8|8|8|
|short|16|16|16|16|
|int|16|32|32|64|
|long|32|32|64|64|
|long long|64|64|64|64|
|pointer|32|32|64|64|
初學者常常會沒有注意到資料的範圍,而不小心 overflow/underflow 產生 bug ,但還有一種是因為 implicit conversion 造成的 bug ,更加難以發現。
### C 語言的自動型別轉換
開頭的例子與我們的直覺似乎不相符,但從數值系統來看卻很正常,這是 C 語言自動轉型所造成的。在左右兩側的變數為不同型別時,C 語言會先做型別轉換,由於 `a` 是一個 unsigned int ,在第 8 行的判斷式中,會先把 -1 轉型為 unsigned int ,其值會變為一個極大的整數 $2^{32}-1$ ,所以結果會是 false 。
類似的例子還有
|expression|result|comment|
|:-:|:-:|:-:|
|2147483647U > -2147483647-1|false| -2147483648 會轉為 unsigned int|
|2147483647 > (int)2147483648U|true| 2147483648U -> -2147483648 |
在 [The C Programming Language 2/e 44 頁](https://www.dipmat.univpm.it/~demeio/public/the_c_programming_language_2.pdf) 指出,隱性型別轉換的大致規則就是範圍小的轉為範圍大的再做運算,但牽涉到無號數時就會非常複雜,因為無號數與有號數的比較是 machine-dependent。
>Conversion rules are more complicated when unsigned operands are
involved. The problem is that comparisons between signed and unsigned values
are' machine-dependent" because they depend on the sizes of the various integer
types. For example, suppose that int is 16 bits and long is 32 bits. Then
-1L < 1U,because 1U,which is an int, is promoted to a signed long. But
-1L > 1UL,because -1L is promoted to unsigned long and thus appears to
be a large positive number
在 [The C Programming Language 2/e Appendix A6](https://www.dipmat.univpm.it/~demeio/public/the_c_programming_language_2.pdf) 中總結了轉換的規則
long double > double > float > unsinged long int > ==long int (?) unsigned int== > int
其中在 long int 與 unsigned int 比較時,還須牽涉到該系統的 long 與 int 的位元數,若 long 的位元數較多,則轉為 long ,反之則轉為 unsigned int。
### 二補數系統
以 8 bit 表示有號整數為例,每個 bit 所表示的數值為:
```graphviz
digraph word{
node[shape=record]
a [label="-2^7|2^6|2^5|2^4|2^3|2^2|2^1|2^0"]
}
```
==注意最左邊的 bit 代表的數字是 $-2^7$ 。==
因此每個 bit 都是 1 時等於 -1 的特性不需要去記,稍微計算後就知道結果 -128+64+32+16+8+4+2+1 = -1 ,所以任意整數與其補數相加為 -1 。
- x + ~x = -1
移項後可得
- -x = ~x+1
即在二補數系統下, ==x 的負數為其補數+1==。利用這個特性,我們可以寫出無分支版本的求絕對值,無分支版本沒有判斷式,亦即其執行時的時間是 deterministic ,在某些應用上這是一個重要的特性,程式碼如下:
```c=1
int absVal(int x)
{
int y = x>>31;
return (x^y) + (~y+1);
}
```
但要小心 `>>` 運算子的行為,在 [C語言規格書](http://www.open-std.org/jtc1/sc22/wg14/www/docs/n1124.pdf) 寫著
>**6.5.7 Bitwise shift operators**
>The result of E1 >> E2 is E1 right-shifted E2 bit positions. If E1 has an unsigned type or if E1 has a signed type and a nonnegative value, the value of the result is the integral part of the quotient of $\frac{E1}{ 2^{E2}}$. If E1 has a signed type and a negative value, the resulting value is implementation-defined.
由以上描述得知,
- E1 是 unsigned 或 nonnegative signed 時, `E1 >> E2` 其值為 $E1/2^{E2}$ 。
- E1 是 signed 且 negative ,是 implementation-defined。也就是有兩種可能性,補 sign bit 或補 `0`。
這個無分支版本的求絕對值一定要在補 sign bit 的情況下才能使用。
### 不精確的浮點數
浮點數的表示方式以 IEEE754 所定義,在 [維基百科](https://zh.wikipedia.org/wiki/IEEE_754) 就有詳細的解說,因此不再贅述。初學程式者會認為浮點數能表示的範圍比整數大的多,因此變數多使用浮點數,就不會遇到 overflow/underflow 的問題,但浮點數最大的問題在於==不精確==,浮點數在計算機內的處理其實遠比整數複雜得多。
- 以 32 bits 浮點數 float 為例,其 fraction 部份佔 23 bits ,所以當整數需要大於24個 bits 表示時,其誤差甚至會大於 1 。(因為 IEEE754 預設正規化浮點數的整數部份為 1 ,所以 fraction 部份只要表示小數部份即可)
我們以一段簡單的程式碼做測試:
```c=1
void floatPrecision(int start)
{
float f;
printf("---start=%d---\n", start);
for (int i = start; i < start + 10; i++) {
f = i;
printf("i=%d, f=%.2f\n", i, f);
}
}
```
當 start 代入 1<<23 時(剛好用 24 bits 可以表示),其輸出為
:::success
---start=8388608---
i=8388608, f=8388608.00
i=8388609, f=8388609.00
i=8388610, f=8388610.00
i=8388611, f=8388611.00
i=8388612, f=8388612.00
i=8388613, f=8388613.00
i=8388614, f=8388614.00
i=8388615, f=8388615.00
i=8388616, f=8388616.00
i=8388617, f=8388617.00
:::
看起來還沒有問題,但如果 start 以 1<<24 代入時,輸出為
:::danger
---start=16777216---
i=16777216, f=16777216.00
i=16777217, f=16777216.00
i=16777218, f=16777218.00
i=16777219, f=16777220.00
i=16777220, f=16777220.00
i=16777221, f=16777220.00
i=16777222, f=16777222.00
i=16777223, f=16777224.00
i=16777224, f=16777224.00
i=16777225, f=16777224.00
:::
可以看到存到浮點數內之後差甚至大於 1,而且捨入後的值有某種規律。
- 當浮點數無法精準表示數值時,會以 round-to-nearest (round-to-zero)的方式捨入。
- 看「捨」與「入」哪邊比較近
- 如果一樣近,也就是最低有效位右邊一位是 1 ,其餘皆為 0 的情況下,會使得最低有效位為 0 的那邊。也就是當最低有效位是 0 的時候會「捨」,反之會「入」。
我們把上面的輸出改為二進位的方式來看,我們輸入的整數為
```graphviz
digraph word{
node[shape=record]
{rank=same; a;b;c;d}
a [label="0|0|0|0|0|0|0|1"]
b [label="0|0|0|0|0|0|0|0"]
c [label="0|0|0|0|0|0|0|0"]
d [label="0|0|0|0|0|0|<ptr>0|0"]
最低有效位 -> d:ptr
}
```
對照剛才上面的例子,把輸出改為 16 進位較好分析。這個例子因為最低有效位右邊只有一位,所以在奇數時都會面臨「捨」或「入」。
:::danger
---start=16777216---
i=1000000, f=16777216.00
i=1000001, f=16777216.00
i=1000002, f=16777218.00
i=1000003, f=16777220.00
i=1000004, f=16777220.00
i=1000005, f=16777220.00
i=1000006, f=16777222.00
i=1000007, f=16777224.00
i=1000008, f=16777224.00
i=1000009, f=16777224.00
:::
|i|最右邊位元組|捨或入|f|
|:-:|:-:|:-:|:-:|
|0x1000000|00000000|不變|16777216.0|
|0x1000001|00000001|捨|16777216.0|
|0x1000002|00000010|不變|16777218.0|
|0x1000003|00000011|入|16777220.0|
|0x1000004|00000100|不變|16777220.0|
|0x1000005|00000101|捨|16777220.0|
|0x1000006|00000110|不變|16777222.0|
|0x1000007|00000111|入|16777224.0|
|0x1000008|00001000|不變|16777224.0|
|0x1000009|00001001|捨|16777224.0|
- 浮點數表示的值,並非均勻分佈。由於浮點數的表示要分成三種,非正規數、正規數、特殊值,接近 0 時會較為密集。
- 特殊值: NaN(Not a Number) 與 無窮大。
---
## 指標
指標是 C 語言令初學者非常頭痛的一個部份,一不小心就會造成 segmentation fault,如果是開發作業系統,甚至會令整個系統 crash ,許多高階程式語言也因此沒有指標變數。
這裡有段單純的程式碼,足夠讓對指標不熟悉的人出錯。
```c=1
void foo(char *s)
{
s = (char *) malloc(sizeof(char) * 15);
}
int main()
{
char *s = NULL;
foo(s);
strcpy(s, "hello world.");
printf("%s\n", s);
free(s);
return (0);
}
```
這段程式編譯後執行,只會出現 segmentation fault ,並不會印出 hello world.
剛接觸指標時都會有一個簡單的例子,傳一個指標進到某個 function 去更改 main 內的變數值,以下有另一個例子。
```C=1
int B = 2;
void func(int *p) { p = &B; }
int main() {
int A = 1;
int *ptrA = &A;
func(ptrA);
printf("%d\n", *ptrA);
return 0;
}
```
在 gcc 編譯後輸出的結果為
:::success
1
:::
C 語言永遠只有 **call by value** ,傳進 function 的只是擁有相同值的另一個自動變數。
:::info
- 在第5行(包含)之前,資料的樣子
```graphviz
digraph structs {
node[shape=record]
{rank=same; structa,structb}
structptr [label="ptrA|<ptr> &A"];
structb [label="<B> B|2"];
structa [label="<A> A|1"];
structptr:ptr -> structa:A:nw
}
```
- 第6行時,傳進 func 後的瞬間,資料變成下圖
```graphviz
digraph structs {
node[shape=record]
{rank=same; structa,structb}
structptr [label="<name_ptr> ptrA|<ptr> &A"];
structp [label="p|<p>&A"]
structb [label="<B> B|2"];
structa [label="<A> A|1"];
structptr:ptr -> structa:A:nw
structp:p -> structa:A:nw
}
```
- func 內做的運算為**將 p 的值改成 &B**
```graphviz
digraph structs {
node[shape=record]
{rank=same; structa,structb}
structp [label="p|<p>&B"]
structptr [label="<name_ptr> ptrA|<ptr> &A"];
structb [label="<B> B|2"];
structa [label="<A> A|1"];
structptr:ptr -> structa:A:nw
structp:p -> structb:B:nw
}
```
:::
圖中可以輕易看出,原本在 main 中的 ptrA 當然沒有改變。寫 C 語言程式碼的時候,搞懂**資料的型別**很重要。
### 利用指標的指標達到預期中的效果
如果上述的例子要達到預期中的結果該如何修改?善用指標的指標,就能達到預期的結果,程式碼如下:
```c=1
int B = 2;
void func(int **p){*p = &B;}
int main() {
int A = 1;
int *ptrA = &A;
func(&ptrA);
printf("%d\n", *ptrA);
return 0;
}
```
畫成圖後,就會明顯看出與前一個例子不同的地方。
:::info
- 在第5行(包含)之前,資料的樣子
```graphviz
digraph structs {
node[shape=record]
{rank=same; structa,structb}
structptr [label="ptrA|<ptr> &A"];
structb [label="<B> B|2"];
structa [label="<A> A|1"];
structptr:ptr -> structa:A:nw
}
```
- 第6行時,傳進 func 的那個 &ptrA,是一個 RValue。(也就是下圖中的 &ptrA(temp))
```graphviz
digraph structs {
node[shape=record]
{rank=same; structa,structb}
structadptr [label="&ptrA(temp)|<adptr> &ptrA"]
structptr [label="<name_ptr> ptrA|<ptr> &A"];
structb [label="<B> B|2"];
structa [label="<A> A|1"];
structptr:ptr -> structa:A:nw
structadptr:adptr -> structptr:name_ptr:nw
}
```
- 進入 func 的一瞬間,會複製一份剛接到的 &ptrA ,產生一個自動變數 p,將 &ptrA 內的值存在其中,因此在那個當下,資料應該是如下圖。
```graphviz
digraph structs {
node[shape=record]
{rank=same; structa,structb}
structadptr [label="&ptrA(temp)|<adptr> &ptrA"]
structp [label="p(in func)|<p> &ptrA"]
structptr [label="<name_ptr> ptrA|<ptr> &A"];
structb [label="<B> B|2"];
structa [label="<A> A|1"];
structptr:ptr -> structa:A:nw
structadptr:adptr -> structptr:name_ptr:nw
structp:p -> structptr:name_ptr:nw
}
```
- 在 func 只有一行程式,把 p 指向到的值換成 &B
```graphviz
digraph structs {
node[shape=record]
{rank=same; structa,structb}
structadptr [label="&ptrA(temp)|<adptr> &ptrA"]
structp [label="p(in func)|<p> &ptrA"]
structptr [label="<name_ptr> ptrA|<ptr> &B"];
structb [label="<B> B|2"];
structa [label="<A> A|1"];
structptr:ptr -> structb:B:nw
structadptr:adptr -> structptr:name_ptr:nw
structp:p -> structptr:name_ptr:nw
}
```
:::
### 陣列的使用
其實就是指標的一種形式。 `a[5]` 可以解釋為從 `a` 這個記憶體位置向後移動 sizeof(a)*5 個 byte ,從這個位置往後取 sizeof(a) 個 byte 來使用。而 `a` 可以是任意型別的變數,甚至是 struct 都沒關係,全看 `a` 的型別來決定要**如何解釋**取出來的資料。
```graphviz
digraph structs {
node[shape=record]
atext [label="a",shape=plaintext]
a [label="<array> |||||<a5> a[5]||||"]
atext -> a:array:nw
a:array:sw -> a:a5:sw
}
```
C 語言的物件,就是從某個記憶體位置開始,往後數個 bytes ,端看如何詮釋這段記憶體空間內所表示的資料。可以是整數、浮點數甚至是一個 struct 。
有了這樣的觀念,就能理解為什麼 `malloc` 需要給 size ;而 `free` 卻只要給一個 pointer 就可以正確運作。
```graphviz
digraph block_ele{
node[shape=record]
payload [label="這裡是 pointer ", shape=plaintext]
ptrofblock [label="這裡是 objHead ", shape=plaintext]
prevblock [label="<prev> ...前一個 obj..."]
block [label="<nextptr> *next|<prevptr> *prev|size|magic_header|<ptr> 這裡是我們要的空間|magic_footer"]
nextblock [label="<next> ...下一個 obj..."]
ptrofblock -> block:nextptr:nw
block:nextptr -> nextblock:next:nw
block:prevptr -> prevblock:prev:nw
payload -> block:ptr:nw
}
```
每一塊 malloc 出來的空間是類似這樣的物件組成的,因為都是相同的 struct ,因此 `*next`、`*prev`、`size`、`magic_header` 占的 bytes 數是固定的。所以只要有 pointer 的位置,就能找到物件開始的位置 `objHead` ,進而得到這塊空間的大小 `size` ,所以 free 根本不需要 size 這個參數。
### 記憶體的運用
多維陣列的使用很常見,以下三種方式構成的二維陣列在使用上完全一樣,但背後的行為卻不同。
```c=1
int a[10][5];
int **b;
int **c;
b = (int **) malloc(sizeof(int *) * 10);
for (int i = 0; i < 10; i++)
b[i] = (int *) malloc(sizeof(int) * 5);
c = (int **) malloc(sizeof(int *) * 10);
c[0] = (int *) malloc(sizeof(int) * 10 * 5);
for (int i = 1; i < 10; i++)
c[i] = (c[i - 1]) + sizeof(int) * 5;
for (int i = 0; i < 10; i++)
free(b[i]);
free(b);
free(c[0]);
free(c);
```
```graphviz
digraph malloc{
node[shape=record]
arr [label="b", shape=plaintext]
arr_a [label="<ptr0> b[0]|<ptr1> b[1]|<ptr2> ...b[9]"]
data1 [label="<ptr1>||||"]
data2 [label="<ptr2>||||"]
data3 [label="<ptr3>||||"]
arr -> arr_a:ptr0:nw
arr_a:ptr0 -> data1:ptr1:nw
arr_a:ptr1 -> data2:ptr2:nw
arr_a:ptr2 -> data3:ptr3:nw
}
```
```graphviz
digraph malloc{
node[shape=record]
arr_a [label="<ptr0> c[0]|<ptr1> c[1]|<ptr2> ...c[9]"]
data [label="<ptr0>|||||<ptr1>|||||...|<ptr2>||||"]
matptr [label="c", shape=plaintext]
arr_a:ptr0 -> data:ptr0:nw
arr_a:ptr1 -> data:ptr1:nw
arr_a:ptr2 -> data:ptr2:nw
matptr -> arr_a:ptr0:nw
}
```
如果我們參考 [malloc](http://danluu.com/malloc-tutorial/) 的實作,就會理解陣列 `c` 的方法對於記憶體來說最為有利
- 不會造成記憶體的破碎。使得記憶體的使用效率提高,減少記憶體的額外花費。
- 可以保證這段記憶體是連續的。這對某些演算法很重要,例如矩陣相乘,甚至可以利用這點來加速。
### 善用指標可以提昇程式的效率
C 語言的函式呼叫永遠**只有 call by value**,在傳入較大的 struct 可能會因為複製而花上更多的時間。但無論是何種型別的變數、多大的物件,只要傳入的是指標(包含指標的指標),大小都是一樣的。
- 增加程式的可擴充性。
- 統一函式的 API ,可以用同樣的 function pointer 指向多個函式,這樣的手法可以用於測試不同演算法。
```c=1
typedef struct eleSorter {
void (*fun)(int *arr, int size);
char *funName;
struct eleSorter *next;
} sorterList;
sorterList *addNode(sorterList *list, char *name, void (*fun)(int *, int));
int main()
{
sorterList *list = NULL;
list = addNode(list, "Quick sort", QuickSort);
list = addNode(list, "Merge sort", MergeSort);
list = addNode(list, "Bubble sort", BubbleSort);
return(0);
}
```
- 變數宣告
- void (*signal(int signum, void (*handler)(int)))(int);
- void **(*d) (int &, char **( *)(char *, char **));
這樣的宣告,並非是故意找麻煩, signal 函式正是 linux 的系統呼叫,可以解釋為
```c=1
// sighandler_t is a function pointer which
// takes a integer parameter and returns nothing.
typedef void (*sighandler_t)(int);
sighandler_t signal(int signum, sighandler_t handler);
```
---
## macro 與 function
macro 與 function 使用上好像很類似,但其背後的行為其實差異很大。
- macro 是由前置處理器直接「置換」程式碼的內容。因此在編譯時期就已經知道結果,對於程式碼的效能會較好,省去了 frame 之間的跳躍。
除此之外,macro 還能降低程式開發的成本,例如在 linux kernel 裡面的 list.h ,就有許多類似
```c
#define list_for_each(pos, head) \
for (pos = (head)->next; pos != (head); pos = pos->next)
```
的程式碼,可以降低開發時常會使用到的功能。
- function call 涉及兩個暫存器(rbp rsp)、區域變數的配置、程式碼的跳躍。對於一個程式來說,這件事情是有成本的。記憶體內 stack 的區塊會增長。
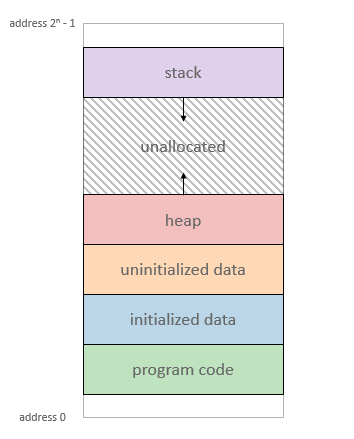
用一個簡單的例子做實驗
```c=1
int sumTo(int k)
{
if (k == 0)
return (0);
else {
printf("%d\n", k);
return (k + sumTo(k - 1));
}
}
```
上面的函式用 k=300000 代入,在我的電腦上,畫面上最後出現的數字是 38223 ,也就是這個函式遞迴呼叫 261,777 次就會引發 segmentation fault ,在這個過程中, stack 不斷增長,紀錄 k 與兩個暫存器的值。
有些演算法利用遞迴呼叫可以寫得優雅,但有時過多的參數與區域變數會使得程式很快就遇到 segmentation fault ,例如影像處理的演算法牽涉到的變數量就很大,這時候只能用其他方法解決,例如
- 使用全域變數
- 改為非遞迴版本
- [Tail call optimization](https://zh.wikipedia.org/wiki/%E5%B0%BE%E8%B0%83%E7%94%A8)
### do...while(0) 巨集
有些重複的程式碼利用 macro 來減少開發量時,可以用 macro 來取代,例如:
```c=1
#define CHECK(x) \
{ \
a...; \
b...; \
}
int main()
{
if(...)
CHECK(x);
else
...;
}
```
這樣的作法確實可以大幅減少開發時的成本,但因為 macro 是直接「置換」,上述程式碼可能根本無法通過編譯,因為通過前置處理器,這段程式碼會變成
```c=1
int main()
{
if(...)
{
a...;
b...;
}; // There is a redundant semicolon.
else
...;
}
```
出現一個多餘的 `;` ,如果硬要修正可以直接將原始程式碼的第10行後面的 `;` 去掉,但這樣子易讀性就會下降,更好的作法是利用 do...while(0) 的巨集。
```c=1
#define CHECK(x) \
do{ \
a...; \
b...; \
}while(0)
int main()
{
if(...)
CHECK(x);
else
...;
}
```
如此一來,整個程式碼看起來就很正常,也達到利用 macro 減少開發成本的目的。
### Reference
[Difference between macro and function](https://www.quora.com/What-is-the-difference-between-a-macro-and-a-function-in-C-programming)
[do...while(0)的使用時機](https://stackoverflow.com/questions/1067226/c-multi-line-macro-do-while0-vs-scope-block)
---
## 最佳化
此處的最佳化我認為用中國的用語「優化」更為妥當,目的在於利用一些簡單的手法加速程式。現代編譯器的聰明程度超乎我們想像,許多現代編譯器可以幫助我們產生等價卻更快的組合語言,無論是利用演算法、編譯器、硬體特性來做加速,都必須對其有一定程度的了解才能做到。
### 消除不必要的重複 call function
偶爾我們會有需要檢索陣列內的每個元素的需求,這時候可能會出現類似以下的程式碼:
```c=1
for(int i=0;i<arr_size(v);i++)
{
v[i] = 2*v[i];
...
}
```
如果陣列的長度在整個過程中都不會改變,那可以改成
```c=1
long length = arr_size(v);
for(int i=0;i<length;i++)
{
v[i] = 2*v[i];
...
}
```
避免 `arr_size` 函式的重複呼叫。
### 減少分支
假設有兩個有號整數 `a`,`b`
```c
if( b<0 ) a++;
```
可以改成
```c
a -= (b>>31);
```
減少分支的判斷。
### Locality of cache
矩陣乘法時常常涉及大量的運算,我們假設有兩個矩陣 `a[1024][800]`,`b[800][1024]` 相乘得到 `dst[1024][1024]` 的矩陣,這樣的運算通常以下方程式碼實作。
最簡單的矩陣相乘演算法
- time complexity : $O(n^3)$
```c=1
// naive matrix multiplication
for (int i = 0; i < a.row; ++i)
for (int j = 0; j < b.col; ++j) {
int sum = 0;
for (int k = 0; k < a.col; ++k)
sum += a.values[i][k] * b.values[k][j];
dst->values[i][j] += sum;
}
```
其實只要稍微修改迴圈的順序,就能得到大幅的加速。
```c=1
// cache-friendly matrix multiplication
for (int i = 0; i < a.row; ++i)
for (int k = 0; k < a.col; ++k) {
int r = a.values[i][k];
for (int j = 0; j < b.col; ++j)
dst->values[i][j] += r * b.values[k][j];
}
```
在 naive algorithm 中, `b.values[k][j]` 一直在取用距離為 `b.col` 的變數,這樣對 cache 的使用不利。要利用 cache 的特性來加速運算,把握兩個重點
1. Temporal locality : 一旦取用過的變數,重複取用。
2. Spatial locality : 取用記憶體中相鄰的變數。
這兩個演算法的時間複雜度一樣,光是改變迴圈的順序,利用 cache 的特性,就可以得到約 3.5 倍的加速。

#### 參考資料
[矩陣乘法](https://hackmd.io/s/HJscCbWgV)
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet