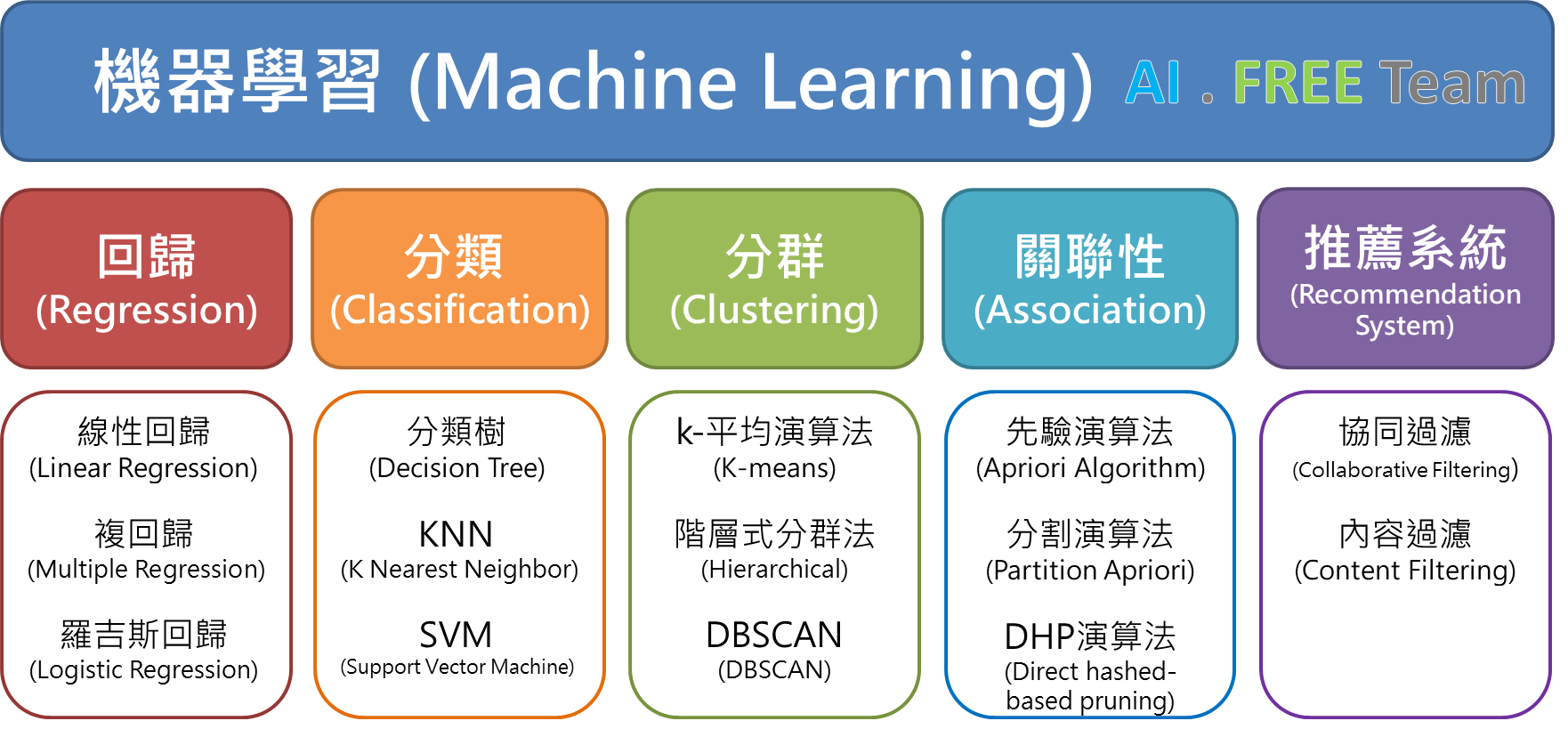
機器學習 入門(X 認識(O 01 === --- 前言 machine learning 的歷史從20世紀初就開始了，並且在多項領域中........ ~~好，剩下自己google!~~ ___  ---  ___  ___ # 名詞解釋 supervised learning training data testing data feature lable regression classification reinforcement learning --- # 機器要學甚麼(正則化演算法) 簡而言之 從model中找出特定的function 而我們的工作就是替機器設定model和找function的方法 那model和function又是甚麼呢? --- ### function 自我們從國中開始 $f(x)$ 就是我們"人生"中不可或缺的東西了 $f(x)$ 就是function 輸入>functio>輸出 --- ### model the set of function 一堆funtio組在一起 例如 $y=ax+b ,a,b∈R$ 就是一種model 你們可能會在別的地方看到的: 線性function:$y=Ax$ 註:$y$和$x$都是向量 --- # 如何達成 我們要根據我們的認知來設定model 並且定義好"好"function的定義 接下來，我會以"以身高估算體重(成年人)"的例子為例來解釋 --- ## set model 先思考一下 $假設0:$也許每個人都有一些基本的體重 $假設1:$也許身高的一次方對體重存在某種關係 $假設2:$也許身高的二次方對體重也存在某種關係 若以x來表示身高,f(x)為體重的話 $f(x)=w_2(x^2) + w_1(x) + w_0$ ,w∈$R$ 會是我們的model $w_2$,$w_1$,$w_0$ 就是各自的權重 ---- ### leanier 線性的定義 $Ax=b$ $A(x_1+x_2)=Ax_1+Ax_2$ 以上面為例 $A$就是[$w_2$,$w_1$,$w_0$] $x$就是[$x^2$,$x$,$1$]$^T$ --- ## fit function 首先，如何知道我們要找的是甚麼function? 好的function產生的結果應該要跟label誤差不大 我們在這邊會決定一個loss function來估算某個function產稱的誤差 loss $l(y,f(x))$ --- ### training/testing data 用以訓練model的資料 用以測試model的資料 --- ### loss function 在這邊$y'$為實際的體重數值、y為預測的值、$l(y',y)$為loss function 我們這邊以差的平方為loss function $l(y',y)=(y'-y)^2$ loss function越大 則代表誤差(lost)越大 ---- 對所有training data 計算loss 則可計算出averge loss(total loss) 而我們的目標則是想辦法讓loss降低(find the mininum of loss)。如果是簡單的funtion我們可以直接用數學的方法直接找到mimum。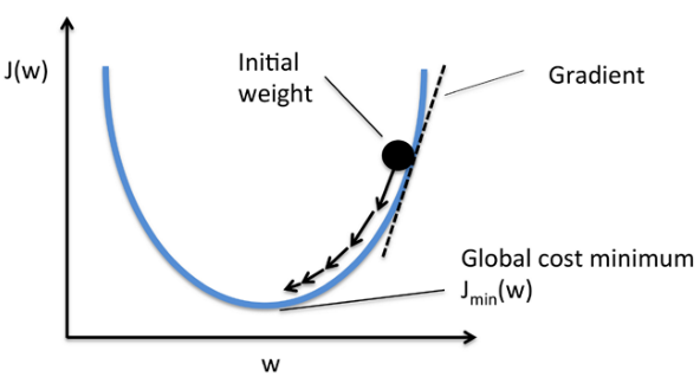這邊的例子應該也可以，不過我們這邊用另外一個方法叫gradient descent 一樣目標是要找到total loss的最小值 --- ### gradient descent  對每一筆training data計算loss，然後算averge loss $al(w)=\dfrac{1}{n}\sum_{i}^{n}(y'^i-y^i)^2$ 帶入$y^i=f(x^i)=w_2x^2 + w_1x + w_0$ $al(w)=\dfrac{1}{n}\sum_{i}^{n}(y'^i-f(x^i))^2$ 我們修改$w$使其下降 --- 我們要做的就是更新$w$ 已縮小a 1 $w_2'=w_2-η\dfrac{∂al(w)}{∂w_2}=w_2-η\dfrac{∂al(w)}{∂f(x)}\dfrac{∂f(x)}{∂w_2}$ 2 $w_2'=w_2-η(\dfrac{1}{n}\sum_{i}^{n}2(y'^i-f(x^i))\cdot -1\cdot\dfrac{∂f(x^i)}{∂w_2})$ 3 $w_2'=w_2-η(\dfrac{1}{n}\sum_{i}^{n}2(y'^i-f(x^i))\cdot -1\cdot (x^i)^2)$ --- ### learning rate $η$????? 別擔心，只是一個係數 雖然在設定這個係數大有學問 不過我們這邊就先固定用一個小小的值就好 --- # 實戰 ## 目標 由身高預測體重 training dataset : 300筆 (身高、體重) [男性](https://drive.google.com/file/d/1ccow5l_IgJicsvoC6v30lvBi5thbkCfl/view?usp=sharing) [女性](https://drive.google.com/file/d/1fJJ4FtmyPy8-AklRZCLwULjlCcEGqbs_/view?usp=sharing) --- ## 流程 step1 載入資料: >複製程式碼 ```python= # =====載入資料===== import numpy as np import pandas from google.colab import files uploaded = files.upload() df=pandas.read_csv('data.csv')#data.csv為檔名 high=df[['hi']].to_numpy() weight=df[['weight']].to_numpy() train_x=high[:250] train_y=weight[:250] test_x=high[250:] test_y=weight[250:] print('OK!') ``` step2 定義我們的model >使用function來完成 ```python= def f(x): global w0,w1,w2 return (x**2)*w2+x*w1+w0 ``` step3 定義loss function >使用function來完成 ```python= def lose(x,y): sum=0 n=len(x) for i in range(n): sum+=(y[i]-f(x[i]))**2 return sum/n ``` step4 計算 loss function對 weight 的微分 >使用function來完成 ```python= def lose_dw0(x,y): sum=0 n=len(x) for i in range(n): sum+=-2*(y[i]-f(x[i])) return sum/n def lose_dw1(x,y): sum=0 n=len(x) for i in range(n): sum+=-2*(y[i]-f(x[i]))*x[i] return sum/n def lose_dw2(x,y): sum=0 n=len(x) for i in range(n): sum+=-2*(y[i]-f(x[i]))*(x[i]**2) return sum/n ``` step5 初始化 weight ,learning rate,epoch > 隨意設定 ```python= w0=5 w1=5 w2=0 learning_rate=0.01 ep=2000 ``` step6 更新 weight >使用for 迴圈重複執行 ```python= for i in range(ep): new_w0=w0-lose_dw0(train_x,train_y)*learning_rate new_w1=w1-lose_dw1(train_x,train_y)*learning_rate new_w2=w2-lose_dw2(train_x,train_y)*learning_rate w0=new_w0 w1=new_w1 w2=new_w2 ``` step7 測試結果 >使用test data ```python= print(lose(train_x,train_y)) print(lose(test_x,test_y)) ``` step8 have fun!! ```python= import matplotlib.pyplot as plt fig, ax = plt.subplots(figsize=(8, 4)) ax.scatter(train_x, train_y) ax.plot(train_x, w2*train_x*train_x+w1*train_x+w0) fig.suptitle('Scatter with regression') plt.show() ``` # 問題思考 ### weight 的初值是否對最終的結果產生影響? ### learning rate 真的只能是固定的? ### 找一次lost是否需要把全部的資料用上? ```python= print(f('要預測體重的身高')) # 預測的體重 ``` # 正解 ```python= def lose(x,y): sum=0 n=len(x) for i in range(n): sum+=(y[i]-f(x[i]))**2 return sum/n def llose(x,y): sum=0 n=len(x) for i in range(n): sum+=(y[i]-ff(x[i]))**2 return sum/n def f(x): global w0,w1,w2 return w2*x*x+w1*x+w0 def ff(x): return 22.6*x*x def lose_dw0(x,y): sum=-2*(y-f(x)) return sum def lose_dw1(x,y): sum=-2*(y-f(x))*x return sum def lose_dw2(x,y): sum=-2*(y-f(x))*x*x return sum def sr_mean(x): n=len(x) m=0 for item in x: m+=item**2 # print((m/n)**0.5) return (m/n)**0.5 w0=1 w1=2 w2=3 learning_rate_0=0.001 learning_rate_1=0.001 learning_rate_2=0.001 leariniglist=[[],[],[]] ep=200 print(lose(train_x,train_y)) for i in range(ep): n=len(train_x) for j in range(n): w0=w0-lose_dw0(train_x[j],train_y[j])*learning_rate_0 w1=w1-lose_dw1(train_x[j],train_y[j])*learning_rate_1 w2=w2-lose_dw2(train_x[j],train_y[j])*learning_rate_2 # w0=new_w0 # w1=new_w1 # w2=new_w2 print(w0,w1,w2) print(lose(train_x,train_y)) print(llose(train_x,train_y)) print(lose(test_x,test_y)) print(llose(test_x,test_y)) print(f(test_x[6]),test_y[6]) ```