---
tags: Linux Kernel
---
# 2022q1 Homework2 (quiz2)
contributed by < `kevinshieh0225` >
> [作業需求](https://hackmd.io/@sysprog/linux2022-homework2)
> [測驗題目](https://hackmd.io/@sysprog/linux2022-quiz2)
## 測驗 `1`:bitwise average
在 binary search 時需要取中間索引,而可能出現以下實作之探討。第一個程式碼明顯可能出現 (a+b) 導致 overflow 的問題,故通常會改以 (low) + (high - low) / 2 做取代
```c
#include <stdint.h>
uint32_t average(uint32_t a, uint32_t b)
{
return (a + b) / 2; // may cause overflow
}
uint32_t average(uint32_t low, uint32_t high)
{
return low + (high - low) / 2;
}
```
以 bitwise 操作改寫:
```c
/**
* 在 uint32_t 上(a >> 1) 等價於 (a / 2) 的操作
* (a >> 1) + (b >> 1) 可理解為 (a / 2) + (b / 2)
* 然而這裡會有問題是若 2 除 a 與 b 的餘數皆為 1,會讓這兩段結果相差 1。
*
* (EXP1) 要補回 (a + b) 在 Least Significant Bit 進位的判斷。
*
* 初步構想:
* (EXP1) = ((a & 1) & (b & 1))
* a & 1 是對 LSB 的取值,如果兩數的 LSB 皆為 1 則必須加上進位數。
* ((a & 1) & (b & 1)) = (a & b & 1)
*/
uint32_t average(uint32_t a, uint32_t b)
{
return (a >> 1) + (b >> 1) + (EXP1);
}
```
:::info
`EXP1` = `a & b & 1`
:::
再次改寫,這次我們用 bitwise 實作加法器原理:
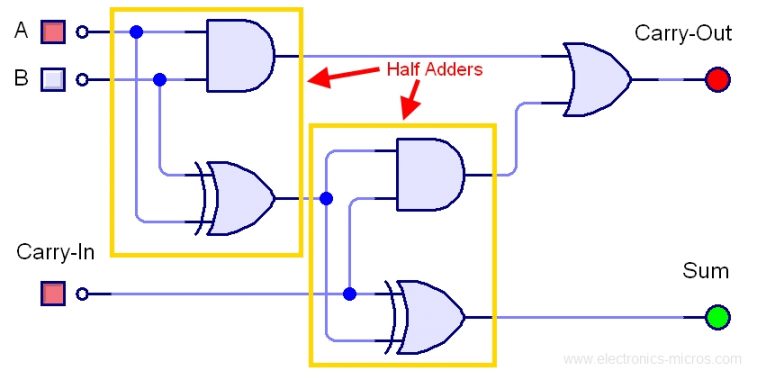
```c
/**
* 一個加法器利用 (a ^ b) 計算 sum,(a & b) 計算 carry-out
*
* 那麼整個無號整數加法 (a + b) 可以視為:((a & b) << 1) + (a ^ b)
*
* 隨後 (a + b) 除 2 即可改寫為:
* (((a & b) << 1) + (a ^ b)) >> 1
* = (a & b) + ((a ^ b) >> 1)
*/
uint32_t average(uint32_t a, uint32_t b)
{
return (EXP2) + ((EXP3) >> 1);
}
```
:::info
`EXP2` = `a & b`
`EXP3` = `a ^ b`
:::
---
## 測驗 `2`:bitwise max
讓我們從文件 [That XOR Trick](https://florian.github.io/xor-trick/) 切入:
```c
/**
* XOR Trick:
* x ^ 0 = x
* x ^ x = 0
* x ^ y = y ^ x
*
* 故若 a > b,return a ^ 0 == a
* ((EXP4) & -(EXP5)) == 0
* 反之 a < b,return a ^ (a ^ b) == b
* ((EXP4) & -(EXP5)) == (a ^ b)
*
* 若 EXP4 == a ^ b
* 在 a > b 時,((a ^ b) & -(EXP5)) == 0
* -(EXP5) == 0x00000000
* EXP5 == 0x00000000
* 在 a < b 時,((a ^ b) & -(EXP5)) == (a ^ b)
* -(EXP5) == 0xffffffff
* EXP5 == 0x00000001
*
* 故 EXP5 等於 a < b,或是 a <= b 也可以
* 因為如果 a == b 的話,不管是回傳 a 或是 b 都是可以的。
*/
uint32_t max(uint32_t a, uint32_t b)
{
return a ^ ((EXP4) & -(EXP5));
}
```
:::info
`EXP4` == `a ^ b`
`EXP5` == `a < b`
:::
### 有號整數 max 實做
我認為上面 max 函式應能使用在有號與無號的整數上。以下我們來看另一種實作。
我們參考〈[解讀計算機編碼](https://hackmd.io/@sysprog/binary-representation#%E4%B8%8D%E9%9C%80%E8%A6%81%E5%88%86%E6%94%AF%E7%9A%84%E8%A8%AD%E8%A8%88)〉中 `min` 的實作原理:
```c
/**
* 首先研究 (diff >> 31) 遮罩的用意:
*
* 若 0 <= diff <= INT32_MAX:
* (diff >> 31) == 0
* (diff & (diff >> 31)) == 0
* 回傳較小值 b
*
* 若 INT32_MIN <= diff < 0:
* 有號整數右移為算術位移
* (diff >> 31) == 0xFFFFFFFF
* (diff & (diff >> 31)) == diff
* 回傳 b + diff == b + (a - b) == a
*/
int32_t min(int32_t a, int32_t b)
{
int32_t diff = (a - b);
return b + (diff & (diff >> 31));
}
```
回來看看有號整數的 `max` 的實作:
```c
/**
* 先從 min 推論 max 作法
*
* 若 0 <= diff <= INT32_MAX:
* (diff >> 31) == 0
* (diff & (diff >> 31)) == 0
* 回傳較大值 a
*
* 若 INT32_MAX <= diff < 0:
* 有號整數右移為算術位移
* (diff >> 31) == 0xffffffff
* (diff & (diff >> 31)) == diff
* 回傳 a - diff == a - (a - b) == b
*/
int32_t max(int32_t a, int32_t b)
{
return a - ((a-b) & (a-b)>>31);
}
```
這種方法相比最初考試的版本還更好理解,但它卻有以下問題:
- 此法無法用於無號整數,因為這個方法是仰賴有號整數右移的性質產生`0x0000`與`0xffff`的遮罩。(無號整數是邏輯右移)
- 此方法須 `INT32_MIN <= (a - b) <= INT32_MAX` 為前提,否則將導致位元溢出。
---
## 測驗 `3` : [greatest common divisor](https://en.wikipedia.org/wiki/Greatest_common_divisor)
```c
/**
* gcd64: 透過輾轉相除法尋找最大公因數
*
* (ref: 維基百科)
* 輾轉相除法基於如下原理:兩個整數的最大公因數等於其中較小的數和兩數相除餘數的最大公因數。
* 例如,252 和 105 的最大公因數是 21(252 = 21 * 12, 105 = 21 * 5)
* 因為 252 − 105 = 21 × (12 − 5) = 147 ,所以 147 和 105 的最大公因數也是 21。
* 在這個過程中,較大的數縮小了,所以繼續進行同樣的計算可以不斷縮小這兩個數直至餘數為零。
* 這時,所剩下的還沒有變成零的數就是兩數的最大公因數。
*
* 程式碼說明:
* 1. 若 u 或 v 任一為 0,則回傳非 0 之數。若兩者皆為 0,則回傳 0。
* 2. 透過 while 進行輾轉相除:
* 透過除數餘數交替,實現輾轉相除。
* (總是將 u 指派為被除數,v 指派為除數,在 v = u % v 時讓除餘數交替)
* 最後直到 v 被除盡後,代表前一個除數是最大公因數,於是回傳其值。
*/
#include <stdint.h>
uint64_t gcd64(uint64_t u, uint64_t v)
{
if (!u || !v) return u | v;
while (v) {
uint64_t t = v;
v = u % v;
u = t;
}
return u;
}
```
以下是等價實作:
```c
/*
* 在此實作中,增加了對 2 的倍數的檢查,也改寫了輾轉相除的演算法。
*
* 1. 若 u 或 v 任一為 0,則回傳非 0 之數。若兩者皆為 0,則回傳 0。
*
* 2. 首先檢查 u,v 是否有 2 次方的公因數:
* !((u | v) & 1) 是在檢查 u,v 的 LSB 是否皆為 0,
* 若是則代表 u,v 是 2 的倍數,一起除以二。
*
* 3. 接著執行改進的輾轉相除法:
* 由於我們已經確保把 u,v 的 2 次方公因數除盡了,所以 u,v 剩值不可能再有 2 的公因數!
* 所以我們在進行輾轉相除同時不斷把 2 的因數除盡,以更快速的尋得剩值的最大公因數。
* 3.1 將 u 的 2 的因數除盡。
* 3.2 執行輾轉相除法:當 v 不為零
* 3.2.1 將 v 的 2 的因數除盡。
* 3.2.2 取餘數的過程:若 u 還是小於 v ,則 v -= u
* 3.2.3 輾轉相除對調:直到 u 跟 v 的大小反轉,便進行輾轉對換。
*
* 4. 最終回傳 (2的shift次方) * u,亦可表達為(u << shift)
*/
#include <stdint.h>
uint64_t gcd64(uint64_t u, uint64_t v)
{
if (!u || !v) return u | v;
int shift;
for (shift = 0; !((u | v) & 1); shift++) {
u /= 2, v /= 2;
}
while (!(u & 1))
u /= 2;
do {
while (!(v & 1))
v /= 2;
if (u < v) {
v -= u;
} else {
uint64_t t = u - v;
u = v;
v = t;
}
} while (COND);
return RET;
}
```
:::info
`COND` = `v`
`RET` = `u << shift`
:::
### x86_64 __builtin_ctz 改寫
`__builtin_ctz` 是 GCC 的內建函式,並非標準函式,但可在 GCC 編譯下加速位元運算的效率。參考 [6.59 Other Built-in Functions Provided by GCC](https://gcc.gnu.org/onlinedocs/gcc/Other-Builtins.html):
>Built-in Function: int __builtin_ctz (unsigned int x)
Returns the number of trailing 0-bits in x, starting at the least significant bit position. If x is 0, the result is undefined.
`__builtin_ctz` 回傳從 LSB 數來的 0-bits 數量。這可以讓我們的程式碼更快速的掌握並除以 2 的倍數。
```c
#include <stdint.h>
uint64_t gcd64(uint64_t u, uint64_t v)
{
if (!u || !v) return u | v;
int shift = min(__builtin_ctz(u), __builtin_ctz(v));
u >>= shift, v >>= shift;
u >>= __builtin_ctz(u);
do {
v >>= __builtin_ctz(v);
if (u < v) {
v -= u;
} else {
uint64_t t = u - v;
u = v;
v = t;
}
} while (v != 0);
return u << shift;
}
```
### gcd 在 linux 核心實作
在 [lib/math/gcd.c](https://github.com/torvalds/linux/blob/master/lib/math/gcd.c) 中我們可以看到兩種 gcd 函式的實作版本,差異在系統定義的 `CONFIG_CPU_NO_EFFICIENT_FFS`:是否 find first set `__ffs` 函式是可用的,若無就改以用 while 迴圈依序檢查處理。
```c
#if !defined(CONFIG_CPU_NO_EFFICIENT_FFS)
unsigned long gcd(unsigned long a, unsigned long b)
...
#else
unsigned long gcd(unsigned long a, unsigned long b)
...
```
以下我們針對使用 `__ffs` 的實作方式作探討:
__ffs 是在 [linux/include/asm-generic/bitops/__ffs.h](https://github.com/spotify/linux/blob/master/include/asm-generic/bitops/__ffs.h) 中定義的函式:
```c
/**
* __ffs - find first bit in word.
* @word: The word to search
*
* Undefined if no bit exists, so code should check against 0 first.
*/
static __always_inline unsigned long __ffs(unsigned long word)
```
舉個例子:
> 32 = 10000,__ffs(34ul) == 5
> 34 = 10010,__ffs(34ul) == 2
稍微了解它的功能後回來看到 `gcd` 程式碼中:
```c
/**
* gcd - calculate and return the greatest common divisor of 2 unsigned longs
* @a: first value
* @b: second value
*
*/
unsigned long gcd(unsigned long a, unsigned long b)
{
// r : 查看 a, b 將所有位元為 1 的位元設定為 1。
unsigned long r = a | b;
// 若 u 或 v 任一為 0,則回傳非 0 之數。若兩者皆為 0,則回傳 0。
if (!a || !b)
return r;
/*
* 太難讀了,以後再研究吧:)
*
*/
b >>= __ffs(b);
if (b == 1)
return r & -r;
for (;;) {
a >>= __ffs(a);
if (a == 1)
return r & -r;
if (a == b)
return a << __ffs(r);
if (a < b)
swap(a, b);
a -= b;
}
}
```
---
## 測驗 `4`:bitset
目的:消除最低位元的 1
bitset & -bitset 可以得出其他為 0,只剩最低位元之位置為 1
如:
> bitset = 01001100
> -bitset= 10110100
> bitset & -bitset = 00000100
> bitset ^ t = 01001000
:::info
`EXP6` = `bitset & -bitset`
:::
---
## 測驗 `5`:[166. Fraction to Recurring Decimal ](https://leetcode.com/problems/fraction-to-recurring-decimal/)
```c
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "list.h"
/**
* 實作 hash table linkedlist node
*/
struct rem_node {
int key;
int index;
struct list_head link;
};
/*
* find: 尋找鍵值
*
* 用 key%size 確認 [0, size-1] 的雜湊值
* 在該欄位尋找 key,若有則回傳 index,若無則回傳 -1
*/
static int find(struct list_head *heads, int size, int key)
{
struct rem_node *node;
int hash = key % size;
list_for_each_entry (node, &heads[hash], link) {
if (key == node->key)
return node->index;
}
return -1;
}
```
```c
/**
* fractionToDecimal: 模擬數學上的整數除法
*
* [step]
* 1. 輸入值為零的處理例外狀況
* 2. 處理輸入值為負號的情況
* 3. 整數除法
* 4. 小數除法
*
* @numerator 被除數
* @denominator 除數
*
* return 除法結果的字串
*/
char *fractionToDecimal(int numerator, int denominator)
{
/* 1.
* 建立 size = 1024 的 char *result 來記錄回傳字串
* char *p 作為 result 的存值處理指標。
*
* 若 denominator 為 0,回傳空字串
* 若 numerator 為 0,回傳 "0"。
*/
int size = 1024;
char *result = malloc(size);
char *p = result;
if (denominator == 0) {
result[0] = '\0';
return result;
}
if (numerator == 0) {
result[0] = '0';
result[1] = '\0';
return result;
}
/* 2.
* 設定 long long n,d 為避免 overflow
* 並且處理 negative situation:
* n,d 取絕對值
* 如果答案為負,先在第一個字串位元插入 '-'
*/
long long n = numerator;
long long d = denominator;
/* deal with negtive cases */
if (n < 0)
n = -n;
if (d < 0)
d = -d;
bool sign = (float) numerator / denominator >= 0;
if (!sign)
*p++ = '-';
/* 3.
* 先做整數位除法。division 與 remainder 分別為商與餘數
* 透過 sprintf 將格式化數據寫入字符串內:
* # int sprintf(char *str, const char *format, ...)
*
* 如果沒有餘數,則直接回傳字串。
*
* [warning] division 可能出現負數嗎?
*/
long long remainder = n % d;
long long division = n / d;
sprintf(p, "%ld", division > 0 ? (long) division : (long) -division);
if (remainder == 0)
return result;
p = result + strlen(result);
*p++ = '.';
/* 4
* 處理小數位字串
*
* 4.1
* 建立 size = 1024 的 char *decimal 來記錄小數字串
* char *q 作為 decimal 的存值處理指標。
* 這個 *decimal 的目的是因為題目要求當循環小數出現時
* 要特別把循環小數的字串用括弧包起來。
* 不方便直接補值操作,所以特別使用新的 buffer 處理。
*
* 使用 hash size = 1333 的 hashtable *heads 來記錄餘數 (remainder)
* 如果重複出現,代表出現循環小數了
*
* [spoiler] 特別注意鍵值所指:
* key: 餘數
* index: 第 n 個小數位置
*
* 由於循環小數開始的位置是不固定的,所以我們用 index 來提示我們這是第幾個位置的餘數
* 也可以得知是從第幾個小數位置開始發生循環。
*/
char *decimal = malloc(size);
memset(decimal, 0, size);
char *q = decimal;
size = 1333;
struct list_head *heads = malloc(size * sizeof(*heads));
for (int i = 0; i < size; i++)
INIT_LIST_HEAD(&heads[i]);
/* 4.2
* 不斷補 0 除值直到餘數終為 0
* 4.2.1 若找到重複的餘數,表示此為循環小數
* pos 是我們循環小數開始的位置,所以我們先將尚未循環的小數點回補到 *result 字串。
* [info] PPP = pos--
* 接著把剩下循環的小數填入在 '(' ')'中間
*
* 4.2.2 如果還沒出現循環小數,那麼把本次鍵值(餘數 remainder 與小數位置 i)
* 先記錄在 hashtable
* [info] MMM = list_add
* EEE = &heads[remainder % size]
*
* 4.2.3 將小數餘商插入 *decimal,並更新餘數(remainder)
*
* 如果離開迴圈,代表整除。故把小數字串接上並回傳
*/
for (int i = 0; remainder; i++) {
int pos = find(heads, size, remainder);
if (pos >= 0) {
while (PPP > 0)
*p++ = *decimal++;
*p++ = '(';
while (*decimal != '\0')
*p++ = *decimal++;
*p++ = ')';
*p = '\0';
return result;
}
struct rem_node *node = malloc(sizeof(*node));
node->key = remainder;
node->index = i;
MMM(&node->link, EEE);
*q++ = (remainder * 10) / d + '0';
remainder = (remainder * 10) % d;
}
strcpy(p, decimal);
return result;
}
```
:::info
`PPP` = `pos--`
`MMM` = `list_add`
`EEE` = `&heads[remainder % size]`
:::
---
## 測驗 `6`:[\_\_alignof\_\_](https://gcc.gnu.org/onlinedocs/gcc/Alignment.html)
從[文件](https://gcc.gnu.org/onlinedocs/gcc/Alignment.html)中關於 \_\_alignof\_\_ 的描述:
> The keyword __alignof__ determines the alignment requirement of a function, object, or a type, or the minimum alignment usually required by a type. Its syntax is just like sizeof and C11 _Alignof.
在理解 `ALIGNOF` 的程式碼前,可以先來理解 `offsetof macro`:
> [offsetof - wikipedia](https://en.wikipedia.org/wiki/Offsetof)
C's offsetof() macro is an ANSI C library feature found in stddef.h. It evaluates to the offset (in bytes) of a given member within a struct or union type, an expression of type size_t.
>
>The offsetof() macro takes two parameters, the first being a structure name, and the second being the name of a member within the structure.
> [Learn a new trick with the offsetof() macro](https://www.embedded.com/learn-a-new-trick-with-the-offsetof-macro/)
```c
// Keil 8051 compiler
#define offsetof(s,m) (size_t)&(((s *)0)->m)
// Microsoft x86 compiler (version 7)
#define offsetof(s,m) (size_t)(unsigned long)&(((s *)0)->m)
// Diab Coldfire compiler
#define offsetof(s,memb) \
((size_t)((char *)&((s *)0)->memb-(char *)0))
/*
* (size_t)( ...6
* (char *) ...4
* &( ...3
* ((s *)0) ...1
* )->memb ...2
* - (char *)0 ...5
* )
* 1: takes the integer zero and casts it as a pointer to s .
*
* 2: dereferences that pointer to point to structure member memb .
* 3: computes the address of memb .
* # the priority of -> is higher than &
*
* 4: casts the result as a pointer to char.
* 5: minus a pointer to char which is casting from 0
*
* 6: return an appropriate data type
*/
```
我對 `offsetof()` 的解釋如下:
- 1: 先將 `0` 轉型為 `struct*`,這麼做是在給定一個起始地址在 `0` 的結構,以便後續對齊並得出該結構成員 `memb` 的地址位移 `offset`。
- 2.3: 指向成員 `memb` 並取其地址
- 4.5: 把 `memb` 和 `0` 的地址相減取得 `offset`。在這裡可注意的是:我們先將地址轉型成 `(char *)` 後才執行運算,意思是我們以一個字節 `(sizeof(char) = 1 byte)` 作為單位來算 `offset`。
- 6: 取得 `memb` 在結構中的位置後回傳 `size_t` 型態的值。
看懂以後我們就來解析 `ALIGNOF`。
```c
/*
* ALIGNOF - get the alignment of a type
* @t: the type to test
*
* This returns a safe alignment for the given type.
*/
#define ALIGNOF(t) \
((char *)(&((struct { char c; t _h; } *)0)->M) - (char *)X)
/*
* (
* (char *) ...4
* &( ...3
* (struct { char c; t _h; } *)0 ...1
* )->M ...2
* - (char *)X ...5
* )
*
*
* 1: takes the integer zero and casts it as a pointer to a struct.
* the struct is define with member with struct { char c; t _h; }
*
* 2: dereferences that pointer to point to structure member M .
* 3: computes the address of M .
* [info] M = _h
*
* 4: casts the result as a pointer to char.
* 5: minus a pointer to char which is casting from X
* [info] X = 0
*/
```
:::info
`M` = `_h`
`X` = `0`
:::
---
## 測驗 `7`:[Fizz Buzz](https://en.wikipedia.org/wiki/Fizz_buzz)
Fizz Buzz 的規則如下
- 從 1 數到 n,如果是 3的倍數,印出 “Fizz”
- 如果是 5 的倍數,印出 “Buzz”
- 如果是 15 的倍數,印出 “FizzBuzz”
- 如果都不是,就印出數字本身
我們若能精準從給定輸入 i 的規律去控制 start 及 length,即可符合 FizzBuzz 題意。
```c
/*
* is_divisible: a faster remainders implementation when the divisor is a constant
*/
static inline bool is_divisible(uint32_t n, uint64_t M)
{
return n * M <= M - 1;
}
static uint64_t M3 = UINT64_C(0xFFFFFFFFFFFFFFFF) / 3 + 1;
static uint64_t M5 = UINT64_C(0xFFFFFFFFFFFFFFFF) / 5 + 1;
```
```c
/*
* FizzBuzz
*
* 1. 用 for 迴圈確認 [1, 100] 的每個數字在 "FizzBuzz Game" 中應該回傳的字串
*
* 2. 檢查數字是否能被 3 與 5 整除,並強制轉型為 uint8_t
* 如果 i 能被 3 整除,div3 是 1,反之為 0。
* 如果 i 能被 5 整除,div5 是 1,反之為 0。
*
* 3. 從 div3, div5 的結果決定我們要擷取的字串長度 length:
* 因為 "Fizz" 和 "Buzz" 皆為 4 個字節,於是我們可以利用這個特性來計算擷取長度:
* 如果有任一 div == 1,則長度 2 << 1 => 4;
* 如果兩個都中了,即再位移一次 4 << 1 => 8。
* [info] KK1 = div3
* KK2 = div5
*
* 4. 用 strncpy 將字串擷取存入 char fmt[9]。
* 第二個參數是 "FizzBuzz%u" 字串起始擷取的位元地址,並擷取字串長度 length。
*
* string literal: "FizzBuzz%u"
* offset: 0 4 8
* 我們來列舉情境:
* case1 (div3 == 0, div5 == 0): offset = 8
* case2 (div3 == 1, div5 == 0): offset = 0
* case3 (div3 == 0, div5 == 1): offset = 4
* case4 (div3 == 1, div5 == 1): offset = 0
*
* 回到參數:&"FizzBuzz%u"[(9 >> div5) >> (KK3)]
* 已知 9 = 1001
* 我們可以推得結果:
* # div3 為 1,讓 9 >> 4 可讓 offset 為 0。
* # div5 為 1,讓 9 >> 1 可讓 offset 為 4。
* # 如果 div3 和 div5 同時 shift 沒關係,因為 0 的右移還是 0。
*
* [info] KK3 = div3 << 2
*/
int main(int argc, char **argv)
{
// 1
for (size_t i = 1; i <= 100; i++) {
// 2
uint8_t div3 = is_divisible(i, M3);
uint8_t div5 = is_divisible(i, M5);
// 3
unsigned int length = (2 << KK1) << KK2;
//4
char fmt[9];
strncpy(fmt, &"FizzBuzz%u"[(9 >> div5) >> (KK3)], length);
fmt[length] = '\0';
printf(fmt, i);
printf("\n");
}
return 0;
}
```
:::info
`KK1` = `div3`
`KK2` = `div5`
`KK3` = `div3 << 2`
:::
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet