###### tags: `Kallies`
# 1. Lehrjahr

### Ohmsches Gesetz

$$ \frac {U}{R \cdot I} $$

---

### Innenwiderstand (Lastverhalten einer realen Spannungsquelle)
$$ R_i= \frac {U_0}{I} - R_L $$

Eine reale Spannungsquelle verhält sich so, als ob in ihr ein Ohm'scher Widerstand vorhanden wäre. Es ergibt sich das folgende ==Ersatzschaltbild==.

U (0)= Quellenspannung /Leerlaufspannung
U (RL)= Klemmenspannung
Ri = Innenwiderstand
RL = Lastwiderstand
I = Stromstärke

---

### 2. Kirchhoffsches Gesetz
==Die Summe aller Spannungen in einer Masche ist 0.==

$$ U_0 + U_R + U = 0 $$

---

### Reihenschaltung von Widerständen


$$ I = I_1 = I_2 = I_3 $$
$$ Rges = R_1 + R_2 + R_3 $$

---

### Parallelschaltung von Widerständen

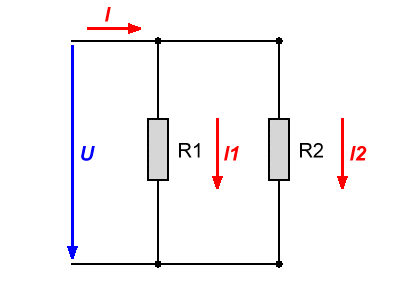
$$ U = U_1 = U_2 = U_3 $$

$$ I_1 = \frac {U}{R_1} $$
$$ I_2 = \frac {U}{R_2} $$

$$ Rges = \frac {R_1 \cdot R_2}{R_1 + R_2} $$
$$ \frac{1}{Rges}= \frac {1}{R_1} + \frac {1}{R_2} + \frac {1}{R_3} $$

---

### 1. Kirchhoffsches Gesetz

==Die Summe aller Ströme in einem Knoten ist 0.==

---

### Leitungswiderstand

Jedes Material hat einen ==eigenen Widerstand==, der von der Atomdichte und Anzahl der freien Elektronen abhängig ist. Der Widerstand wird deshalb auch spezifischer Widerstand genannt. Damit ist der Widerstand gemeint, der sich auf ein bestimmtes Material bezieht.

R [Ω] = Widerstand
ρ [Ωmm²/m] = spezifischer Widerstand
l [m] = Leitungslänge
A [mm²] = Leitungsquerschnitt

Je kürzer die Leitungslänge und je größer der Leitungsquerschnitt des Materials, desto geringer der ohmsche Widerstand. Die Abhängigkeit von der Leitungslänge wird dadurch erklärt, dass die Elektronenbewegung auf einer größeren Strecke stärker gehemmt wird, als auf einer kürzeren Strecke. Durch die Änderung der Leitungslänge und des Querschnitts ändert sich nur der ohmsche Widerstand.
Der spezifischer Widerstand ist eine ==Materialkonstante== und ist somit ein fest definierter Wert.
Daraus ergibt sich folgende Formel:

$$ R = \frac {ρ \cdot l} {A} $$

---

### Spannungsteilerregel

Ein Spannungsteiler besteht im Regelfall aus zwei Widerständen, an denen sich die ==Gesamtspannung Uges in zwei Teilspannungen aufteilt==. Die Grundform ist der unbelastete Spannungsteiler, der einer Reihenschaltung aus zwei Widerständen entspricht.

Spannungsteiler werden verwendet, um Arbeitspunkte (Spannungsverhältnisse) an aktiven Bauelemente einzustellen.

$$ \frac {R_1}{R_2} = \frac {U_1} {U_2} $$
$$ \frac {R_1}{R_g} = \frac {U_1}{U_g} $$

---

### Gemischte Schaltung

Eine gemischte Schaltung ist eine Mischung aus Reihen- und Parallelschaltungen.


#### Widerstände berechnen

Bei so einer Schaltung muss man zu erst "hinten anfangen" mit der Berechnung der Widerstände.

Hier ist das die Parallelschaltung mit den Widerständen R1 und R2. Diese beiden werden zusammengefasst.

Das Ergebnis davon kann dann als Reihenschaltung mit R3 verrechnet werden.

Das Ergebnis davon ist der Gesamtwiderstand der gemischten Schaltung.

#### Teilströme und Teilspannungen berechnen

Mithilfe des vorher berechneten Gesamtwiderstands und der gegebenen Spannung kann man mit dem ohmschen Gesetz den Gesamtstrom berechnen.

Mit diesem kann man die Teilspannung an R3 berechnen. Die Differenz zu der Gesamtspannung ist dann die Teilspannung an R1 und R2.

Mithilfe der Teilspannung an R1 und R2 kann man die Teilströme an diesen berechnen.

---

### Leistung
**Leistung P (in Watt)** = ==umgesetzte Energie in einer Zeit / in einer Schaltung==
$$ P=U \cdot I $$

Durch entsprechendes Einsetzen mit dem Ohm'schen Gesetz erhält man: <br>

$$ P= \frac {U^2}{R} $$

$$ P=R \cdot I^2 $$

---

### Arbeit

Arbeit ist die ==umgesetzte Leistung in einer Zeit (t)==. Dementsprechend gilt:

$$ W = P \cdot t $$

---

### Spannungsquelle
#### Reihenschaltung:

$$ Uges = U_1 + U_2 $$

#### Parallelschaltung:

$$ Iges = I_1 + I_2 $$
Die Spannung U befindet sich zwischen den Potenzialen der Spannungsquellen.

---

### LED

- Spannung ==1,6V < U_max < 2,4V==
- Strom ==15mA < I_max < 25mA==
- ==Vorwiderstand==, um Spannung und Strom zu begrenzen
- am Vorwiderstand muss so viel Spannung abfallen, dass die LED in ihrem Optimalbereich kommt
$$ R_V = \frac{U-U_F}{I_F} $$


---

### Diode


**Kennlinie einer Diode in Durchlassrichtung**
Beim Durchgang durch eine Silicium-Diode fällt die Spannung ==relativ konstant um 0,7V== ab – weitgehend unabhängig von der Stärke des fließenden Stroms. Das Ohmsche Gesetz ist somit nicht auf Dioden anwendbar.


Legt man eine entgegengesetzte Spannung U_S an, so ==sperrt die Diode== (Diode in Sperrrichtung schalten). Wird der Spannungswert überschritten, so nimmt die (ebenfalls in Gegenrichtung) fließende Stromstärke I_S rasant zu; die Diode kann dabei schnell überhitzt bzw. zerstört werden.

#### Auf jeder Diode sind zwei charakteristische Werte aufgedruckt:

- Die Spannung sagt aus, mit welcher Spannung die Diode maximal in Sperrichtung betrieben werden darf.
- Die Stromstärke gibt an, welcher Strom maximal (in Durchlassrichtung) durch die Diode fließen darf.

---

### Z-Diode

Z-Dioden werden im Gegensatz zu Dioden bewusst so gebaut, dass sie ab einer ==bestimmten (Durchbruch-)Spannung in Gegenrichtung leitfähig== werden. In Durchlassrichtung verhält sich eine Z-Diode wie eine normale Diode.
Eine Z-Diode verhält sich in Sperrichtung im Wesentlichen so wie eine normale Diode in Vorwärtsrichtung. Hat beispielsweise eine Z-Diode eine ==Durchbruchspannung von U=5,6V, so kann erst ab dieser Spannung ein Strom in Sperrichtung fließen==. Bei höheren Spannungen nimmt die Stromstärke stark zu; die auf der Diode angegebene Maximal-Stromstärke sollte allerdings nicht überschritten werden.

---
### Brückenschaltung

Eine Brückenschaltung besteht aus vier Widerständen. Dabei handelt es sich um ==zwei parallele Reihenschaltung von jeweils zwei Widerständen==.
Durch U_0 wird die Brückenschaltung mit Spannung versorgt. Die ==Ausgangsspannung wird zwischen A und B== gemessen.

Von einer **abgeglichenen Brücke** wird gesprochen, wenn die Widerstandswerte so gewählt sind, dass die ==Ausgangsspannung U_AB 0V== beträgt. Für das Verhältnis der Widerstände gilt:

$$ \frac{R1}{R2} = \frac{R3}{R4} $$

#### Dieser Zusammenhang kann folgendermaßen hergeleitet werden:

Die Spannung U_AB entspricht der Spannungdifferenz von U_A und U_B:

$$ U_{AB}=U_A - U_B $$

Für den abgeglichenen Fall gilt:

$$ U_{AB}=0 $$

Damit ergibt sich:

$$ 0=U_A - U_B $$

$$ U_A = U_B $$

An dieser Stelle können die Spannungen U_A und U_B über den Spannungsteiler berechnet werden.

Für U_A gilt:

$$ U_A=U_0 \cdot \frac{R_2}{R_1+R_2} $$

Für U_B gilt:

$$ U_B=U_0 \cdot \frac{R_4}{R_3+R_4} $$

Eingesetzt in die obige Formel ergibt sich:

$$ U_A=U_B $$

$$ U_0 \cdot \frac{R_2}{R_1+R_2}= U_0 \cdot \frac{R_4}{R_3+R_4} $$

Nachdem beide Seiten durch U_0 dividiert werden:

$$ \frac{R_2}{R_1+R_2}= \frac{R_4}{R_3+R_4} $$

Nun kann auf beiden Seiten der Kehrbruch gebildet werden:

$$ \frac{R_1+R_2}{R_2}= \frac{R_3+R_4}{R_4} $$

Anschließend werden die Brüche aufgeteilt:

$$ \frac{R_1}{R_2}+\frac{R_2}{R_2}= \frac{R_3}{R_4}+\frac{R_4}{R_4} $$

$$ \frac{R_1}{R_2}+1= \frac{R_3}{R_4}+1 $$

Nach Subtraktion von -1 ergibt sich die Formel für die abgeglichene Brückenschaltung:

$$ \frac{R_1}{R_2}= \frac{R_3}{R_4} $$

Bei der **unabgeglichenen Brückenschaltung** ist das Verhältnis der Widerstände so, dass die ==Ausgangsspannung U_AB nicht 0V== beträgt.

$$ \frac{R_1}{R_2} \neq \frac{R_3}{R_4} $$

$$ U_{AB} \neq 0V $$

Um für diesen Fall die Ausgangsspannung U_AB zu bestimmen, müssen zunächst die Spannungen U_A und U_B bestimmt werden und anschließend ihre Differenz ermittelt werden.

Für die Ausgangsspannung gilt:

$$ U_{AB}=U_A-U_B $$

Für die Teilspannungen U_A und U_B ergibt sich:

$$ U_A=U_0 \cdot \frac{R_1}{R_1+R_2} $$

$$ U_B=U_0 \cdot \frac{R_T}{R_3+R_T} $$

---

### Kondensator
In diesem kann ==elektrische Ladung bzw. elektrische Energie gespeichert werden==. Ein Kondensator besteht aus zwei leitenden Schichten, die durch einen Isolator voneinander getrennt sind. Der so genannte Plattenkondensator stellt eine einfache Bauform des Kondensators dar. Dieser besteht aus einem Paar voneinander isolierter Metallplatten, die mit je einem Pol einer Spannungsquelle verbunden sind.

#### Aufladung
$$ U(t) = U_0 \cdot (1-e^{-\frac{t}{𝜏}}) $$
$$ I(t) = I_0 \cdot (e^{-\frac{t}{𝜏}}) $$
t = Zeit [s]
R = Widerstand
C = Kondensatorkapazität [F]
𝜏 = Zeitkonstante [s]

==𝜏 (Tau) = 63% vom Übrigen geladen
5 𝜏 = vollständig geladen==

#### Entladung
$$ U(t) = U_0 \cdot e^{-\frac{t}{𝜏}} $$
$$ I(t) = -I_0 \cdot e^{-\frac{t}{𝜏}} $$

---

### Transistor

Transistoren sind ==Halbleiter-Bauteile, die als Schalter, Regler und Verstärker fungieren==. Transistoren werden insbesondere verwendet, um ==Ströme zu schalten, zu verstärken oder zu steuern==. Ein Transistor kann auch wie ein ==elektrisch regelbarer Widerstand== eingesetzt werden.
Häufig werden so genannte „bipolare“ Transistoren eingesetzt. Diese bestehen aus drei Halbleiterschichten, wobei je nach Reihenfolge der Dotierungen zwischen ==npn- und pnp-Transistoren== unterschieden wird. Die drei Anschlüsse eines bipolaren Transistors werden ==Kollektor C, Basis B und Emitter E== genannt.


#### npn-Transistoren
Ein npn-Transistor besteht aus drei Halbleiter-Schichten, wobei die beiden äußeren eine negative und die mittlere Schicht eine positive Dotierung aufweisen. Der Aufbau entspricht einem doppelten n-p-Übergang.


Gewöhnlich verläuft der zu steuernde Hauptstrom zwischen dem Kollektor C und dem Emitter E. Die Wirkungsweise des Transistors wird dabei durch die Stromstärke bestimmt, die durch die Basis B zum Emitter E fließt:

- Fließt durch die ==Basis B kein Strom==, so ist die Kollektor-Emitter-Strecke CE des ==Transistors gesperrt==. Er entspricht dabei einem unendlich großen Widerstand beziehungsweise einem geöffneten Schalter.
- Fließt ein ==schwacher Strom durch die Basis B==, so wird die Kollektor-Emitter-Strecke CE ==leitfähig==; es wird also ein Vielfaches des Basis-Stroms durch die Kollektor-Emitter-Strecke durchgelassen. Je nach Art der Transistor-Schaltung entspricht die Wirkungsweise des Transistors einem elektrisch regelbaren Widerstand oder einer leitenden Verbindung (fast) ohne Widerstand.

#### pnp-Transistoren
Ein pnp-Transistor besteht ebenfalls aus drei Halbleiter-Schichten, wobei die beiden äußeren eine positive und die mittlere Schicht eine negative Dotierung aufweisen.

Da die Schichten eines pnp-Transistors im Vergleich zu einem npn-Transistor eine genau umgekehrte Dotierung aufweisen, müssen auch die ==Ströme in die entgegengesetzte Richtung== fließen. Im Schaltzeichen ist dies dadurch gekennzeichnet, dass der Pfeil nicht von der Basis weg, sondern zur Basis hin zeigt.

==**Eselsbrücke**: npn = nicht gepiekt, pnp = gepiekt==