<style> .reveal .slides { text-align: left; font-size:35px } </style> ## 圖上遍歷 & 樹論 ---- - 建圖方法 - 圖上 DFS/BFS 怎麼遍歷 - 樹上 DFS/BFS 怎麼遍歷 - 樹的基本演算法 - 圖&樹經典例題 --- ## 建圖方式 * 鄰接矩陣 * 鄰接串列 * 邊陣列 ---- ## 鄰接矩陣(Adjacency Matrix) - $n\times n$ 的矩陣，其中 $A_{ij}$ 代表點 $i$ 是否連通或是指向點 $j$ - 若為帶權圖則 $A_{ij}$ 存 $i$ 到 $j$ 的邊權 - 若圖有重邊也可以令 $A_{ij}$ 存邊 $(i,j)$ 的數量 - 空間複雜度 $O(n^2)$ - 遍歷圖的時間複雜度 $O(n^2)$ - 由於複雜度高因此不常用 ---- ## 無向圖 無權圖用 0/1 表示兩點間是否有連邊 無向圖的矩陣會是對稱的  ---- ## 有向圖 沒有連邊的點對通常權重設為 0  ---- ## 鄰接串列(Adjacency Lists) - $n$ 個串列，第 $i$ 個串列存 $i$ 所指向的邊(點) - 若為帶權圖，則串列可以存 pair(目標點,邊權) - 通常以 vector 實作，也就是 vector 陣列或二維 vector - 空間複雜度 $O(m)$ - 遍歷圖的時間複雜度 $O(m)$ - 最常使用的儲存方式 ----  ----  ---- ### 無權無向圖 在點 $u$ 和點 $v$ 之間連邊 ```cpp= vector<int> edge[100005]; for(int i = 0, u, v; i < m; i++){ cin >> u >> v; edge[u].push_back(v); edge[v].push_back(u); } ``` ---- ### 帶權有向圖 新增一條點 $u$ 指向點 $v$ 權重為 $w$ 的邊 ```cpp= vector<pair<int, int>> edge[100005]; for(int i = 0, u, v, w; i < m; i++){ cin >> u >> v >> w; edge[u].push_back(make_pair(v, w)); } ``` ---- ### 初始化 ```cpp= void init(){ for(int i = 0 ; i <= n; i++){ edge[i].clear(); } } ``` ---- ## 邊陣列(Edge List) - 開一個 pair 陣列把所有邊儲存起來 - 用於最小生成樹 - 不適合拿來遍歷 ---- #### 無權邊 ```cpp= pair<int, int> edges[100005]; for(int i = 0; i < m; i++){ cin >> edges[i].first >> edges[i].second; } ``` #### 帶權邊 ```cpp= struct Edge{ int u, v, w; }edge[100005]; for(int i = 0; i < m; i++){ cin >> edge[i].u >> edge[i].v >> edge[i].w; } ``` --- ## 深度優先搜索(Depth-First-Search,DFS) - 優先往深的地方走 - 通常以遞迴實作，直觀好寫(也可以使用stack取代遞迴) - 時間複雜度$O(E)$(若用鄰接串列) - 由於好寫，以及遞迴方便維護，有很多好的性質，因此是最常用的搜索方法 - 然而遞迴過深有可能導致stack overflow(RE)，遇到時只得改成用迴圈+stack實作(或一些毒瘤方法) ---- ## 實作範例 ```cpp void dfs(int x){ vis[x]=1; for(int i:edge[x]){ if(!vis[i]) dfs(i); } } ``` ----  ---- ## 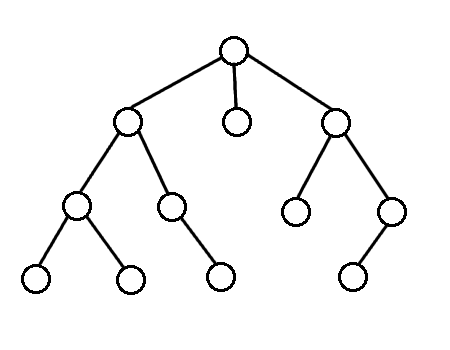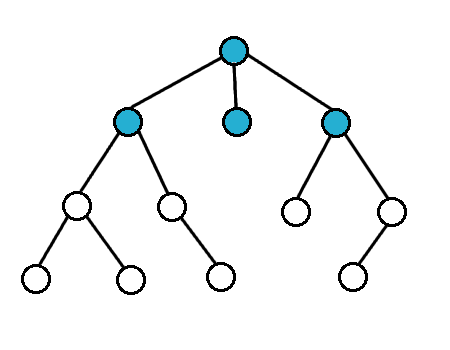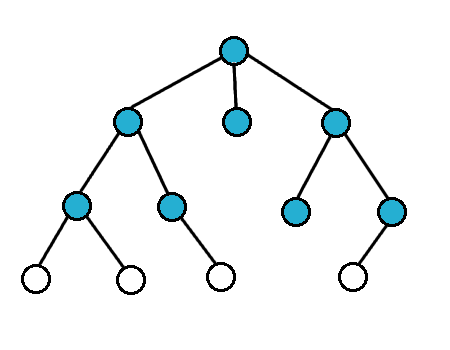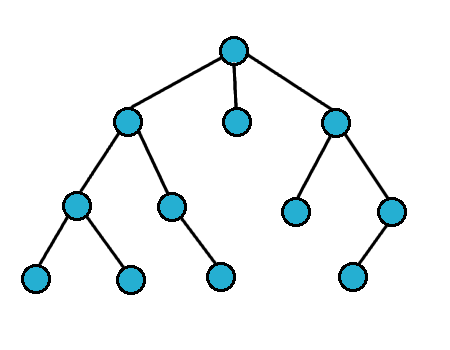廣度優先搜索(Breadth-First-Search,BFS) - 從起點開始往外散開 - 以迴圈+queue實作，寫起來較麻煩 - 對於無權圖，BFS可找出到起點的最短路徑 - 時間複雜度$O(E)$(若用鄰接串列) - 由於較難寫因此較少用，常用在找不帶權最短路 ----  ---- ```cpp bool vis[MXN]; void bfs(int s){ queue<int> q; q.push(s); vis[s]=1; while(!q.empty()){ int x=q.front();q.pop(); for(int i:edge[x]){ if(!vis[i]) q.push(i),vis[i]=1; } } } ``` ---- ## 無向圖最短路 由於 BFS 是一層一層的， 從起點開始往外遍歷，同一層都遍歷過才往下一層遍歷。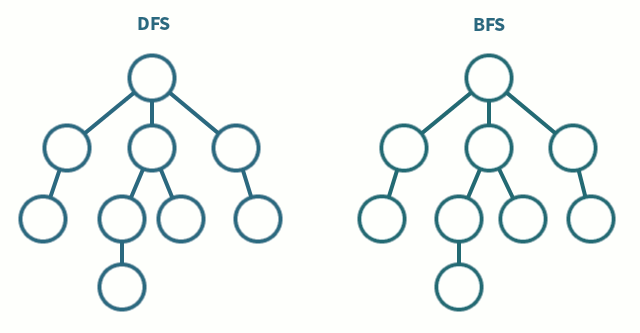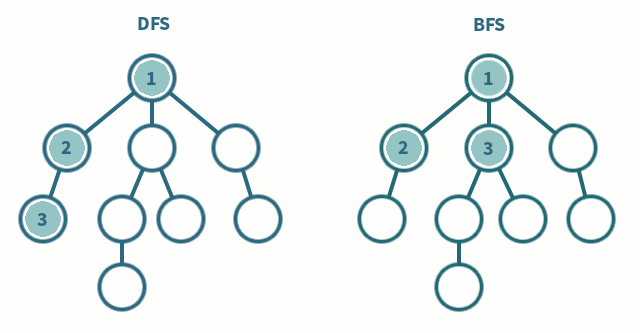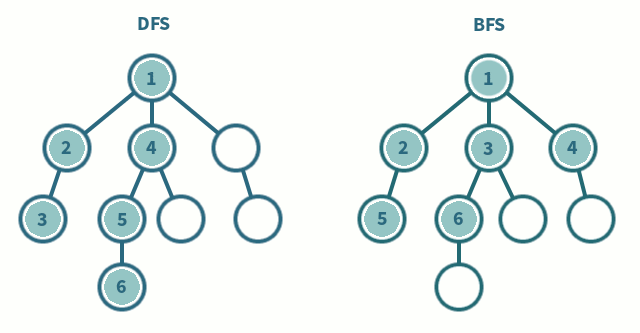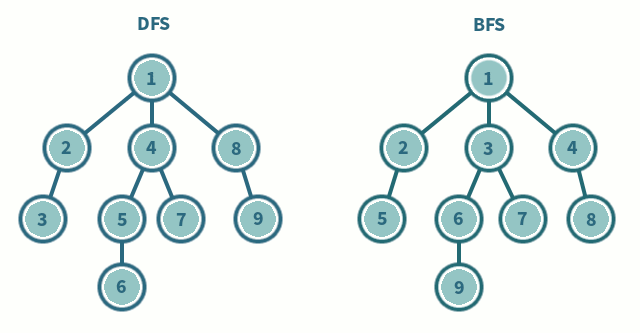 因此走到當前節點時會是從起點到自己最短的 ---- 多開一個 dis 記錄從起點到自己最短距離 ```cpp= bool vis[MXN]; int dis[MXN]; void bfs(int s){ queue<int> q; q.push(s); vis[s]=1; dis[s]=0; while(!q.empty()){ int x=q.front();q.pop(); for(int i:edge[x]){ if(!vis[i]){ q.push(i); vis[i]=1; dis[i] = dis[x]+1; } } } } ``` --- ## 樹上DFS 由於沒有環，只要不要走回頭路就不會走到重複的點，因此多傳遞一個參數"父節點"就不需要visit陣列判斷點是否造訪過 ---- ```cpp void dfs(int x,int father){ for(int i:edge[x]){ if(i!=father) dfs(i,x); } } ``` ---- ## 樹上BFS 由於沒有環，只要不要走回頭路就不會走到重複的點，因此多傳遞一個參數"父節點"就不需要visit陣列紀錄點是否造訪過 從樹根開始，嚴格按照層次來訪問節點。 BFS 過程中也可以順便求出各個節點的深度和父親節點。 ---- ```cpp void bfs(int s){ queue<pair<int,int>> q; q.push(make_pair(s,0)); while(!q.empty()){ auto [x,y]=q.front();q.pop(); for(int i:vec[x]) if(i!=y) q.push(make_pair(i,x)); } } ``` ----  --- ## 樹的基本演算法 ---- ### 深度 求出一棵有根樹每個節點的深度 - 子節點深度為父節點+1(或邊權) - 根節點的深度為0(或1，視題目要求) ```cpp void dfs(int x,int father) { for(int i:edge[x]) { if(i!=father) d[i]=d[x]+1,dfs(i,x); } } ``` ---- ### 高度 求出一棵有根樹每個節點的高度 - 一個點的高度為所有子節點中，高度最高者+1 - 葉節點的高度為0(或1，視題目要求) ```cpp void dfs(int x,int father) { h[x]=0; for(int i:edge[x]) { if(i!=father) dfs(i,x),h[x]=max(h[x],h[i]+1); } } ``` ---- ### 子樹大小 求出一棵有根樹中以每個節點的為子樹的大小(節點數量) - 一個點的子樹大小為 1+$\sum_{i}sz[子樹_i]$ - 葉節點的子樹大小為1 ```cpp int dfs(int x,int father) { sz[x]=1; for(int i:edge[x]){ if(i!=father){ sz[x]+=dfs(i,x); } } return sz[x]; } ``` --- ## 經典例題 樹例題 - 樹重心 - 樹直徑 圖例題 - 二分圖判定 - 遍歷網格圖(水窪問題) - 網格圖最短路(走迷宮) - 倒水問題 ---- ## [樹重心](https://vjudge.net/contest/676945#problem/K) 求一棵樹的重心，以下是重心的定義： - 如果在樹中選擇某個節點並刪除，這棵樹將分為若干棵子樹，統計子樹節點數並記錄最大值。取遍樹上所有節點，使此最大值取到最小的節點稱為整棵樹的重心。 ---- 以這圖為例： <div style="position: absolute; left: 60%; top:60%;">  </div> 砍掉點 1 ，剩下的最大子樹為 2-5-6-7 ， sz 為 4 砍掉點 2 ，剩下的最大子樹為 1-3-4 ， sz 為 3 砍掉點 5 ，剩下的最大子樹為 1-2-3-4-6 ， sz 為 5 所以樹重心為 點2 ---- - 樹的重心也不一定唯一  上圖樹重心為 1 和 2 ---- ## 怎麼找樹重心 關鍵的地方在於，要找到刪掉某個點後，剩下最大的子樹的 sz 為多少，假設要刪掉點 x，要去拿 x 的所有的子樹 sz 以及 x 往上的樹的 sz  假設要刪掉 2 ，除了要檢查 5 和 6 的子樹大小，還要檢查 2 上方的子樹大小，大小為 (n - (2的子樹大小) ) ---- 因此先預處理子樹大小 ```cpp! int sz[N]; vector<int>edge[N]; int dfs(int x,int father){ sz[x]=1; for(int i:edge[x]){ if(i==father)continue; sz[x]+=sz[i]; } return sz[x]; } ``` ---- 對於一個點，去找他的孩子的子樹大小以及上方的子樹大小 ```cpp! int cen_sz=inf,cen=-1; void find_cen(int x,int father){ //找孩子sz int mx_sz=0; for(int i:edge[x]){ if(i==father)continue; mx_sz=max(mx_sz,sz[i]); } //找上方的樹sz mx_sz=max(mx_sz,n-sz[x]); if(cen_sz>mx_sz){ cen_sz=mx_sz; cen=x; } //算完就往下遞迴算 for(int i:edge[x]){ if(i==father)continue; find_cen(i,x); } } ``` 這樣就找到重心了 ---- 另外還有一個名詞叫[樹中心](https://www.tutorialspoint.com/centers-of-a-tree)，跟樹重心類似，只是判斷的條件從 sz(大小) 變成 deep(深度)。 ---- ## [樹直徑](https://vjudge.net/contest/676945#problem/E) 求出一棵樹最遠兩點的距離 - 先任選一點作為根，將其視作有根樹 - 考慮分治法：直徑可能 1. 經過根節點，也就是前兩高度 2. 不經過根節點，也就是在某棵子樹上，因此遞迴計算子樹的答案再取max - 兩者再取max即為答案 ---- ```cpp int ans; int dfs(int x,int father){ int mh1=0,mh2=0,cur; for(int i:edge[x]){ if(i!=father){ cur=dfs(i,x); if(cur>mh1) mh2=mh1,mh1=cur; else if(cur>mh2) mh2=cur; } } ans=max(ans,mh1+mh2); return mh1+1; } ``` ---- #### 另解 1. 任選一點開始做 DFS，找出最遠(深)的點，記為 mx 2. 從 mx 開始做 DFS，其與最遠點的距離即為直徑(也就是第二次DFS的高度+1) ---- ```cpp int md,mx; void dfs(int x,int father,int d=0){ if(d>md) md=d,mx=x; for(int i:edge[x]){ if(i!=father) dfs(i,x,d+1); } } int find_diameter(){ md=-1; dfs(0,0); md=-1; dfs(mx,mx); return md; } ``` ---- ## 二分圖判斷 判斷題目給你的圖是不是一個二分圖 - 二分圖：一個無向圖中的點可以被分成兩個集合，使得同集合內的點互不相鄰 - 換句話說：黑白染色將圖上的點塗成黑或白，使得每條邊的兩端必不同色 ----  - 左邊是一個二分圖，因為它可以被分成左右兩側的集合，兩側左側塗黑，右側塗白 - 右側不是一個二分圖，因為不管怎麼塗兩種顏色，一定有一條以上的邊兩端顏色都一樣 ---- ### 如何判斷二分圖 - 選擇一個點開始塗黑or白，接著一直往下走，塗成另外一個顏色，一直這樣遞迴下去 - 在塗色之前要先判斷這個點的鄰居顏色是否跟目前要塗的顏色一樣，如果有任意一個顏色一樣，則這張圖不是二分圖 ---- code be like: ```cpp! bool is_bigraph=1; int color[N];//0:沒塗色 , 1:黑色 , 2:白色 void dfs(int x,int x_color){ color[x]=x_color; for(int i:edge[x]){ if(color[x]==color[i]){//遇到一樣的顏色，不是二分圖 is_bigraph=0; } } for(int i:edge[x]){ if(color[i]==0){//沒塗過色 dfs(i,(x_color==1?2:1)); } } } dfs(1,1);//把1塗成黑色 ``` ---- ## [水窪問題](https://zerojudge.tw/ShowProblem?problemid=f493) 給定 $n\times m$ 大小的矩陣，0 代表沒有水，1 代表有水， 問有多少個水窪。 ex ```cpp 3 4 0 0 0 0 1 0 1 1 1 0 1 0 ans : 2 ``` ---- ## 解法 遍歷整個矩陣，每次遇到水就把那攤水使用 BFS/DFS 跑過一次全部消除， 消除完就可以獲得數量。 ---- ## 網格圖遍歷 ```cpp= bool vis[1005][1005]; // 紀錄每個位置是否有走過 int arr[1005][1005]; // 紀錄水窪 void dfs(int x, int y){ if(vis[x][y] || arr[x][y] == 0) return; vis[x][y] = 1; arr[x][y] = 0; if(x+1 < n) dfs(x+1, y); if(x-1 >= 0) dfs(x-1, y); if(y+1 < m) dfs(x, y+1); if(y-1 >= 0) dfs(x, y-1); } ``` ---- 改用迴圈遍歷周圍格子點 ```cpp= bool vis[1005][1005]; // 紀錄每個位置是否有走過 int arr[1005][1005]; // 紀錄水窪 int dx[4] = {1,-1,0,0}; int dy[4] = {0,0,1,-1}; bool safe(int x, int y){ return x >= 0 && x < n && y >= 0 && y < m; } void dfs(int x, int y){ if(vis[x][y] || arr[x][y] == 0) return; vis[x][y] = 1; arr[x][y] = 0; for(int i = 0; i < 4; i++){ if(safe(x+dx[i], y+dy[i])){ dfs(x+dx[i], y+dy[i]); } } } ``` ---- ## [走迷宮問題](https://zerojudge.tw/ShowProblem?problemid=a982) 給定一個 $n\times n$ 的二維整數數組，用來表示一個迷宮，數組中只包含 $0$ 或 $1$，其中 $0$ 表示可以走的路，$1$ 表示不可通過的牆壁。 最初，有一個人位於左上角 $(1,1)$ 處，已知該人每次可以向上、下、左、右任意一個方向移動一個位置。 請問，該人從左上角移動至右下角 $(n,n)$ 處，至少需要移動多少次。 ---- ## 解法 由於每次轉移都是從上下左右移動過來的， 所以只需要從起點開始將可到達的地方全部塞進去， 另外開一個陣列紀錄起點到他的最短距離。 ---- ## [倒水問題](https://vjudge.net/problem/UVA-10603) 給容量分別為 $a,b,c$ 的三杯水，倒法是一杯水到另一杯水倒到自己空或是別人滿為止，一開始 $a,b$是空的 $c$ 是滿的問是否能得到d的水如果不能則輸出 $d'$ (小於 $d$ 最大的容量) sample : ```cpp input 2 1 3 6 4 1 12 15 7 output 3 4 14 7 ``` ---- ## 解法 考慮每一個狀態當成一個節點， 把倒水後的狀態當成連向的節點建邊會形成一張有向圖  ----  (2,3,1) 把 c 的水倒到 a 中 (2,3,1) $\to$ (3,3,0) ---- ## 儲存節點狀態 可以宣告一個結構把每種容量的狀態紀錄起來 並用 map 紀錄每種狀態是否已經走過 ```cpp struct item{ int a, b, c; }; map<item, int> dis; int bfs(item start, item target){ queue<item> que; que.push(start); while(!que.empty()){ item it = que.front(); que.pop(); if(it == target){ return dis[it]; } // 窮舉每種倒水的情況 if(!dis.count(item(it.a + it.c, it.b, 0))){ //c->a dis[item(it.a + it.c, it.b, 0)] = dis[it]+1; que.push(item(it.a + it.c, it.b, 0)); } //c->b, a->b, a->c, b->c, b->a } } ``` ---- ## 畫圖工具 - [graph editor](https://csacademy.com/app/graph_editor/) - [graph online](https://graphonline.ru/en/) ---- [練習題單](https://vjudge.net/contest/676945#overview)