<style> .reveal .slides { text-align: left; font-size:32px; } </style> # Classic DP Introduction to Competitive Programming 3/13 --- - Classic DP Problems - 複習基本DP - 01背包 vs 無限背包 - 有限背包 & 二進制拆分 - Subset Sum - $O(nlog(n))$ LIS - Edit Distance - LCS 轉 LIS - 滾動 --- ## DP Review ---- DP在幹嘛? 切割子問題，壓成狀態，求解。 DP能幹嘛? 計數，找最佳解。 ---- 我要怎麼切割子問題? 一個常見的手法就是對集合狀態下手 像背包問題 $$dp(S) \leftarrow dp(\{x\}\backslash S)$$ 這就是取或不取 $x$ 來做轉移 ---- 可是這樣會有 $O(2^n)$ 的狀態 ( $n$ 是物品個數)， 但我們可以發現一個物品取或不取是沒有順序問題的，因此我們可以只考慮物品在任意的排序 (對第 $n$ 個物品而言順序沒差)下前 $n-1$ 個物品的答案，就能轉移考慮前 $n$ 個物品的答案。 我們就能這樣轉移 $$dp_n \leftarrow dp_{n-1}$$ 此時狀態就會降到 $O(n)$ (負重自己列) ---- 但如果今天是考慮的答案會受取的順序而影響，狀態是不一定能壓下來的，詳見之後的 Bitmask DP。 我們還有很多堂課可以見面 :D --- ## 01背包 vs 無限背包 vs 有限背包 ---- 背包:具有負重上限 $W$，拿的東西總重不超過 $W$。 問能拿的最大物品價值和。 0/1背包:每個物品拿或不拿，且至多拿一個。 無限背包:可以拿不只一個，可以一直拿。 有限背包:物品限量，最多拿某個量個物品。 ---- 0/1背包: 希望各位都記得，不過這邊複習一下滾動。 基本轉移 ```cpp for(int i = 1; i <= n;++i){ for(int w = c[i]; w <= W;++w) dp[i][w] = max(dp[i][w],dp[i-1][w-c[i]]+v[i]); //dp[i][w] 考慮物品1~i且負重上限為w的答案。 } ``` ---- 滾動: $dp[i][w]$ 要轉移過來只會用 $dp[i-1][w-c_{i}]$ 又 $c_{i} > 0 \ s.t. \ w-c_{i} < w$ 讓 $w$ 從大到小遍歷，這樣就不會讓 $dp'[w-c_{i}]$是由第$i$個物品轉移的，所以這樣就會是合法轉移。 ```cpp for(int i = 1; i <= n;++i){ for(int w = W; w >= c[i];--w){ dp[w] = max(dp[w],dp[w-c[i]]+v[i]); } } ``` ---- 無限背包: 既然能一直取，我們只要考慮當前重量 $w$ 所有轉移的可能性就好了，那就是全部東西都拿拿看。 ```cpp for(int w = 0; w <= W;++w){ for(int i = 1; i <= n;++i){ dp[w] = max(dp[w],dp[w-c[i]]+v[i]); } } ``` --- ## 有限背包 & 二進制拆分 ---- ## 有限背包 第 $i$ 個物品能取至多 $k_{i}$ 個，把他看成0/1背包， 也就是有 $\sum k_{i}$ 個物品，這樣複雜度會是 $O((\sum k_{i}) * W)$ 有點爛。 ---- ## 二進制拆分 把 $K = k_{i}$ 個物品分成 $1個、2個、4個、8個、\cdots、2^{\lfloor{logK}\rfloor-1}$個 為一組和一組$K-(1+2+4+8+\cdots+2^{\lfloor{logK}\rfloor-1})$個的。 剛好能在dp上窮舉取 $0,1,\cdots ,k_{i}$ 個第 $i$ 個物品的所有可能性。 ---- here's why: $1、2、4、8、\cdots、2^{\lfloor{logK}\rfloor-1}$的取或不取剛好能湊出 $[0,2^{\lfloor{logK}\rfloor}-1]$ 間的所有整數加上 $K-(1+2+4+8+\cdots+2^{\lfloor{logK}\rfloor-1}) = K-(2^{\lfloor{logK}\rfloor}-1)$ 則可湊出 $[K-(2^{\lfloor{logK}\rfloor}-1),K]$間的所有整數。 又因為 $K-(2^{\lfloor{logK}\rfloor+1}) \leq -1$ 所以 $(K-(2^{\lfloor{logK}\rfloor}-1)) -(2^{\lfloor{logK}\rfloor}-1) \leq 1$ 聯集起來就是 $[0,K]$。 這技巧叫二進制拆解，哪都能用 ( 我不會構造題 😭 ) 。 ---- 範例Code $i*2 \leq k \rightarrow i \leq 2^{\lfloor{logK}\rfloor-1}$ ```cpp #define pp pair<int,int> #define PB push_back int s = 0; vector<pp> A; //目前物品最多拿 k 個 for(int i = 1; i * 2 <= k; i *= 2){ s += i; A.PB({i*w,i*c}); // i 個一綑 } A.PB({(k-s)*w,(k-s)*c}); //最後一組 ``` ---- 會二進制拆解後就能以 $O(N*logK*W)$ 的複雜度把有限背包當0/1背包做。 *等價$N\lfloor{logK}\rfloor$個物品* --- ## Subset Sum ---- ## Subset Sum 給你一個集合 $S = \{A_{1},A_{2}, \cdots ,A_{n}\}$ 再給你一個 $K$ 問你是否有個子集 $Q \subseteq S$ 使得 $\sum_{Q} A_{i} = K$ ex. S = {1,2,3}, K = 5 那 K = 2 + 3, 所以可以湊出來 ---- 假設 $\sum_{S}A_{i} \leq 10^6$ 同樣地這也是個取跟不取的問題 所以我們能輕鬆的列出轉移式 ```cpp vector<bool> dp(MXW+1); dp[0] = 1; // 0 就是不取東西就能湊出來 for(int i = 0; i < n;++i){ for(int w = MXW; w >= A[i]; --w){ dp[w] = dp[w] | dp[w-A[i]]; //dp[w] : w 這個數能不能被湊出來 } } ``` 但你會發現這樣轉移好像有點慢 $O(n*MXW)$ ---- 你會發現我們只需要知道 w 這個數能不能湊出來只要存 0/1 就好。 這時就能用bitset (空間$\div 32$) 然後用bitset就能把第二圈壓掉。 你會發現當bitset長這個樣子 ```cpp // 0 1 2 3 4 5 6 7 8 9 A bs = {1 1 0 0 1 0 0 0 0 0 0} //能湊出的數: 1、4 (bs<<5) = {0 0 0 0 0 1 1 0 0 1 0} //再多考慮 5 這個數時 5、6、9 就能被湊出來 ((bs<<5)|bs) = {1 1 0 0 1 1 1 0 0 1 0} //所以考慮 5 時這個bitset會變這樣 ``` 也就是第二圈轉移能用bitset的位元運算壓掉 因為當下能湊出數字為 bs 時 (bs << x) 指一定要取 x 這個數後能湊出的所有數 (在 bs 的第 i 個位置為 1 的數，在 (bs << x) 裡會在 x + i 為 1) bs | (bs << x) 就是取跟不取都考慮到 ---- 轉移就會變這樣 ```cpp const int MXW = 1e6; bitset<MXW> dp; // bitset記得要開常數 dp[0] = 1; for(int i = 0; i < n;++i){ dp = (dp<<A[i]) | dp; } ``` 而這個位元運算就能把複雜度變這樣 $O(n*MXW/ 32)$ bitset很多運算都非常快，如果你發現複雜度卡在 1e9 之類的你就嘗試看看bitset，因為能直接快32倍。 --- 等等要吞證明，休息一下 --- ## $O(nlog(n))$ LIS ---- ## $O(nlog(n))$ LIS 複習，對於一個序列 $A,|A| = n$ , 以 $A_i$ 為結尾的LIS長度為 $$L_i = max(L_j)+1 \ where \ (i>j \land A_i > A_j)$$ 當 $A_i$ 在找 $A_j$ 時，不妨把 $A_{1,\cdots,i-1}$ 排序使得 $p$ is a permutation of $(1,\cdots,i-1)$ $s.t.$ $$A_{p_1} \leq A_{p_2} \cdots \leq A_{p_{i-1}} \quad and \quad A'=(A_{p_1},\cdots,A_{p_{i-1}})$$ $let$ $k = lowerbound(A',A_{i})$ 這樣符合 $A_i > A_j$ 的 $j$ 就會是 $j \in S = \{p_{1},\cdots,p_{k-1}\}$ 接下來只要找到屬於這個 $S$ 的 $j$ 中最大的 $L_{j}$ 我們就能轉移了。 ---- 我們不妨觀察一下這個集合，會發現當 $A_{x} \leq A_y$ $\land$ $L_x \geq L_y$ where $x,y \in S \land x\neq y$ 此時能從 $y$ 轉移的值都能由 $x$ 轉移，因此我們能把 $y$ 丟掉。 所以對於一個任意的 $L_j$ 值，我們只要留最小的 $A_j$，因此一個 LIS長度只會對到唯一一個 $A_j$。 以及 $L_{x} < L_{y} \rightarrow A_x < A_y$ $(x\neq y)$ 反證一下，因為當 $A_x \geq A_y$ 時 $x$ 就會被丟掉。 根據以上關係我們能構建一個序列 ($L=1 \cdots LIS$都會出現恰巧一次)。 $dp_{(L=1)} = A_{p'_{1}} ,dp_{(L=2)} = A_{p'_{2}} \cdots,dp_{(L=LIS)} = A_{p'_{LIS}}$ ---- 然後同樣手法 $$A_{p'_1} < A_{p'_2} \cdots < A_{p'_{LIS}}$$ $$dp=(A_{p'_1},\cdots,A_{p'_{LIS}})$$ $$let \ k = lowerbound(dp,A_{i})$$ $L_{j}=k-1$ 就是我們要找的轉移值 ---- 接下來要把 $A_{i},$ $L_{i}=k-1+1$ 也丟進 $dp$ 維護 會發現 $A_{i}$ 如果要出現在 $dp$ 裡只能在 $dp_k$ 的位子 1. 如果 $dp_{k}$ 沒值 (也就是 $k > LIS$) 那 $dp_{k}$ 就會是 $A_{i}$。 2. 否則 $dp_{k}$ 就是由左邊過來第一個大於等於$A_{i}$的值， 根據前面的證明，我們就能把原本的 $dp_{k}$丟掉，所以$dp_k$也會變成$A_{i}$。 所以結論就是 $dp_{k} := A_{i}$ ---- 範例Code ```cpp #define PB push_back #define all(v) (v).begin(), (v).end() vector<int> dp; for(int i = 0; i < n;++i){ auto it = lower_bound(all(dp),A[i]); if(it == dp.end()){ dp.PB(A[i]); }else{ *it = A[i]; } } cout << dp.size() << '\n'; ``` --- ## Edit Distance ---- ## Edit Distance 給你兩個字串 $S,T$ ，每次可以刪除、替換、插入一個字，問你最少的步驟數使得兩字串相等。 ex. S = abc T = aecc 把 T 的 e 刪掉 -> T = acc 然後再把中間的 c 換成 b -> T = abc = S 這樣就是兩步，且是最少。 ---- 在討論序列問題時我們時常考慮做完前$i$個的case來做轉移，像LIS就是 $dp[i] =$ 考慮$A_{1\sim i}$序列的最大答案來轉移。 所以我們不妨考慮再只看 $S$ 的前 $i$ 個字元和 $T$ 的前 $j$ 個字元時答案 $let \ n = |S|, m = |T|$ $dp[i][j] = 把\ S[1...i]\ 和\ T[1...j]\ 變成一樣字串的最少步驟$ 則 $dp[n][m]$ 就會是我們要的答案 ---- 轉移: 1. 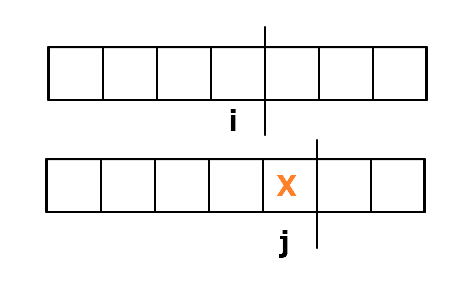刪除操作: 如果刪除 $T_{j}$ 則，$dp[i][j] = dp[i][j-1] + 1$ 因為你可以這樣看字串:  所以不管刪除是沒後效性的，(別自己把字串並上去) 刪除 $S_{i}$ 是等價的 ---- 2. 插入操作: 那要插哪個字，要插在哪? 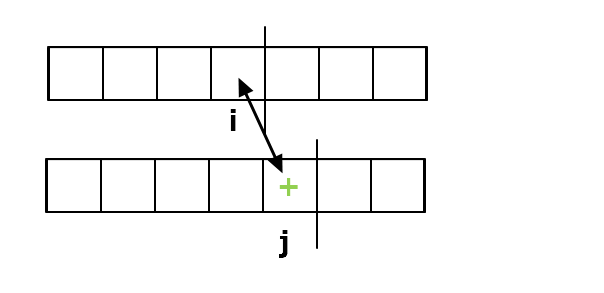假設你亂插，那只為徒增把 $S$ 變成 $T$ 的成本， 所以我們想必是插一個對方沒有的字元:  接下來有個問題: 那插入後不是會讓整個字串變長嗎這樣狀態不就會一直長? ---- 對，但不對 如果你把一個字元插在 $T_{j}$ 的位子那原本的 $T_{j}$ 會跑到 $T_{j+1}$ 但你先不要讓他跑， 你不必真的插入，根據前面我們會插一個 $S$ 有的字元，那我們就插 $S_{i}$ 到 $T_{j}$ 的位子， 你會發現這樣在情況下，$S_{i} = T_{j}$ 那此轉移就會是 $dp[i-1][j-1]+1$ 但因為我們沒有真的把字元插進去，所以等價 $T$ 是不變的，但我們變相的用插入的動作刪掉 $S_{i}$， 所以轉移就變 $dp[i][j] = dp[i-1][j]+1$ 跟前面的刪除 $S_{i}$ 的轉移是一樣的。 ---- 3. 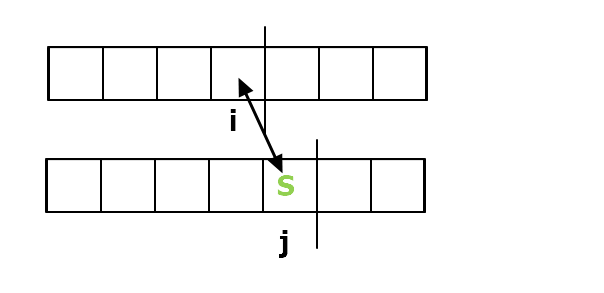替換操作: 等價你刪掉一個字再把一個字插回去，但成本只算你一次  那把 $T_{j}$ 換成$S_{i}$ 後我們只要看 $1 \cdots i-1$ 和 $1 \cdots j-1$ $dp[i][j] = dp[i-1][j-1]+1$ ---- 這樣我們就都列完了，但有個問題就是初始狀態怎麼開? 對於 $dp[0][j]$ 而言，$0$ 個字元變成 $j$ 個那成本就是 $j$ 所以全部合起來就變: ```cpp //我懶 #define forr(i,n) for(int i = 1; i <= n;++i) const int inf = 1e18; void solve(){ string S,T; cin >> S >> T; int n = S.size(); int m = T.size(); S.insert(S.begin(),'$'); //把字串變 1-base T.insert(T.begin(),'$'); vector dp(n+1,vector<int>(m+1,inf)); dp[0][0] = 0; forr(i,n) dp[i][0] = i; //初始化 forr(j,m) dp[0][j] = j; forr(i,n) forr(j,m){ //記得從小到大轉移 if(S[i] == T[j]) dp[i][j] = dp[i-1][j-1]; //相等當然不用轉 else{ dp[i][j] = min({ dp[i-1][j] + 1, //刪除 Si 或 插在 Tj dp[i][j-1] + 1, //刪除 Tj 或 插在 Si dp[i-1][j-1] + 1, //替換 Tj 或 Si }); } } cout << dp[n][m] << '\n'; } ``` --- ## LCS to LIS ---- 先來複習 LCS 給你兩個字串 $S$、$T$ 問你最長共同子序列 (subsequence) * 子序列定義 : 對一於一個字串，他的子序列是通過刪除若干個或0個字元後將剩下字元在不改變原來的順序並起來的字串。 ex. abcde 的子序列有 ace 、ade 但 adc 不是。 在過去的轉移方式和Edit Distance一樣，是考慮$S$、$T$的前綴子串的答案來轉移 $dp[i][j]=$ $S_{1 \cdots i}$ 和 $T_{1 \cdots j}$ 的最長共同子序列長度 如果 $S_{i}=T_{j}$ 那 $dp[i][j] = dp[i-1][j-1] + 1$ 否則那 $dp[i][j] = max(dp[i-1][j],dp[i][j-1])$ ---- 我們觀察一下LCS會長怎樣 ( 圖中橘色的子序列 )  ---- $n = |S| , m = |T|$ 考慮 $A = \{(i,j) \ where \ S_{i} = T_{j} \}$ 你會發現 LCS 會是最長的長得像這樣的序列 $b : (2,1) \ a : (3,3) \ c : (5,5)$ 沒錯，這就是依照二維偏序的遞增序列。 ---- 所以 LCS 就是你把$S$、$T$相同字元的index溝成的pair拿去做二維偏序的最長遞增子序列(LIS)。 像前面那頁的，以 a 為共同字元構成的 pair 有$(1,3)、(1,6)、(3,3)、(3,6)$ 不過，二維LIS是啥鬼? ---- 你把 $(x,y)$ 照 $x$ 排序他就會變回看起來像一般的LIS  但其實不全然，因為你得第一維也嚴格遞增 ( 不能拿到同一個 x ，這樣等同同個字元用兩次 ) 但字元不重複的情況下是好的 ( 當然 ) ---- 回顧2024李秀上的dp  事實上複雜度是有可能壓不下來的，因為在考慮到相同字母配對後，需要處理LIS序列長度就會回到$O(n^2)$的量級(如果相同字元太多)。 所以這做法能幹嘛? ---- 處理排序的LCS。 你會發現你可能開不了$|S| * |T|$的dp 但因為他是排序所以等價每個字元都只出現一次，這樣空間就壓掉了。 --- ## 滾動 ---- 為什麼要會滾動? <span> <br><!-- .element: class="fragment" data-fragment-index="1" --></span> <span>我在賽中沒有好好滾，一直用unodered_map開狀態 <br><!-- .element: class="fragment" data-fragment-index="1" --></span> ----  <span>結果就是我們在賽中TLE了3小時 : ( <br><!-- .element: class="fragment" data-fragment-index="1" --></span> ---- 好，所以怎麼好好滾? 其實重點就在狀態順序跟會不會重疊。 最常見的例子就是前面的背包問題，也就是 $dp[i][一坨狀態]$ 從$dp[i-1][一坨狀態]$ 來，那我可以只保留 $dp[一坨狀態]$ 的資訊，因為你只需要知道你的上一個就好。 那你不滾掉空間就是會大嘛，但還有一點，也就是我前面說的TLE的事情。 ---- 先來個簡單的 illustration  假設下一個狀態的值域不會跟前一個狀態疊在一起，但你強行用 unodered_map 或 map 之類的裝 (以為會少) ---- 比方說 ```cpp= map<int,int> dp; for(int i = 0; i < n;++i){ map<int,int> ndp; for(auto [a,b]:dp){ for... 一坨轉移，並轉移到ndp上 } dp = ndp; } ``` 那這時候就有極大的可能會把上一個狀態的值域也遍歷到，複雜度就會呈現 $1+2+3+ \cdots + n = O(n^2)$ 但每個狀態的值域事實上是 disjoint(互不相交) 的，所以跑完轉移等於跑完整個所有狀態的聯集 那複雜度其實是 $O(n)$ 由於目前主題有點難遇到這種事情發生 ( 通常會發生在樹背包、狀壓之類的 ) ---- 像這種需要好好分析值域的問題 (才能把複雜度壓下來)。 ```cpp= for(int a = min(rr,sz[x]); a >= -min(rr,sz[x]); --a) pd[a+ofs] = dp[x][a+ofs]; for(int a = -min(rr,sz[x]); a <= min(rr,sz[x]); ++a){ if(!pd[a+ofs]) continue; for(int b = -min(rr,sz[u]); b <= min(rr,sz[u]); ++b){ if((a+b+ofs) >= 2*ofs) continue; if(!dp[u][b+ofs]) continue; if((a+b) < -rr) continue; dp[x][(a+b)+ofs] += (1LL * pd[a+ofs] * dp[u][b+ofs]) % mod; dp[x][(a+b)+ofs] %= mod; } } ``` 但這部分比較複雜，今天就不分析，但這告訴我們狀態要好好算。 目前的題目最多會用到的滾動就是把空間 $O(n*C) \to O(C)$。 --- 很多時候dp的正確性會比Greedy或數學題來的更好推，所以當你不知道Greedy是不是真的對的時候可以想想dp，以及特別的dp會在數值範圍上面有特徵，可以多看看題目給的數字範圍來推斷狀態要怎麼開。 --- 我放的有點小多，但蠻多水題的，寫一下嘛🥺 [題單連結](https://vjudge.net/contest/698248#overview)