<style> .reveal .slides { text-align: left; font-size:35px; } </style> ## 線段樹 1 Introduction to Competitive Programming 3/20 ---- - 線段樹是什麼？ - 如何實現單點加值 - 如何實現區間查詢 ---- ## 結構 <center> <img src="https://hackmd.io/_uploads/HJnJ139tp.png" width="700px"> </center> ---- <center> <img src="https://hackmd.io/_uploads/S1pC1n5t6.png" width="700px"> </center> 我們會用陣列表示一顆線段樹 假設總共有 $n$ 個數字 樹高為 $\lceil \log n \rceil + 1$ 節點數為 $2^{\lceil \log n \rceil + 1} - 1$ 我們可以把陣列大小開 $4 * n$ （ $2^{\lceil \log n \rceil + 1} - 1 < 4 \times 2^{\log n}$ ） ---- <center> <img src="https://hackmd.io/_uploads/S1pC1n5t6.png" width="700px"> </center> 當前節點的index為$i$ 左子節點為$2i$ 右子節點為$2i+1$ ---- 如果一段區間的資訊可以透過兩個子區間的資訊來合併 就可以使用線段樹 每個節點存取一段區間的資訊 透過合併不同節點的資訊可以獲得任何一段區間的答案 ---- # 簡單例題 給一個長度為$n$的陣列$a$，有$q$個操作，分為以下2種： - $1$ $l$ $r$ 詢問$[l,r]$區間的最大值 - $2$ $x$ $v$ 把$a_x$設為$v$ $1 \le n,q \le 2*10^5$ ---- <img src="https://hackmd.io/_uploads/BJ0lnrr2yl.png" width="700px"> <!-- 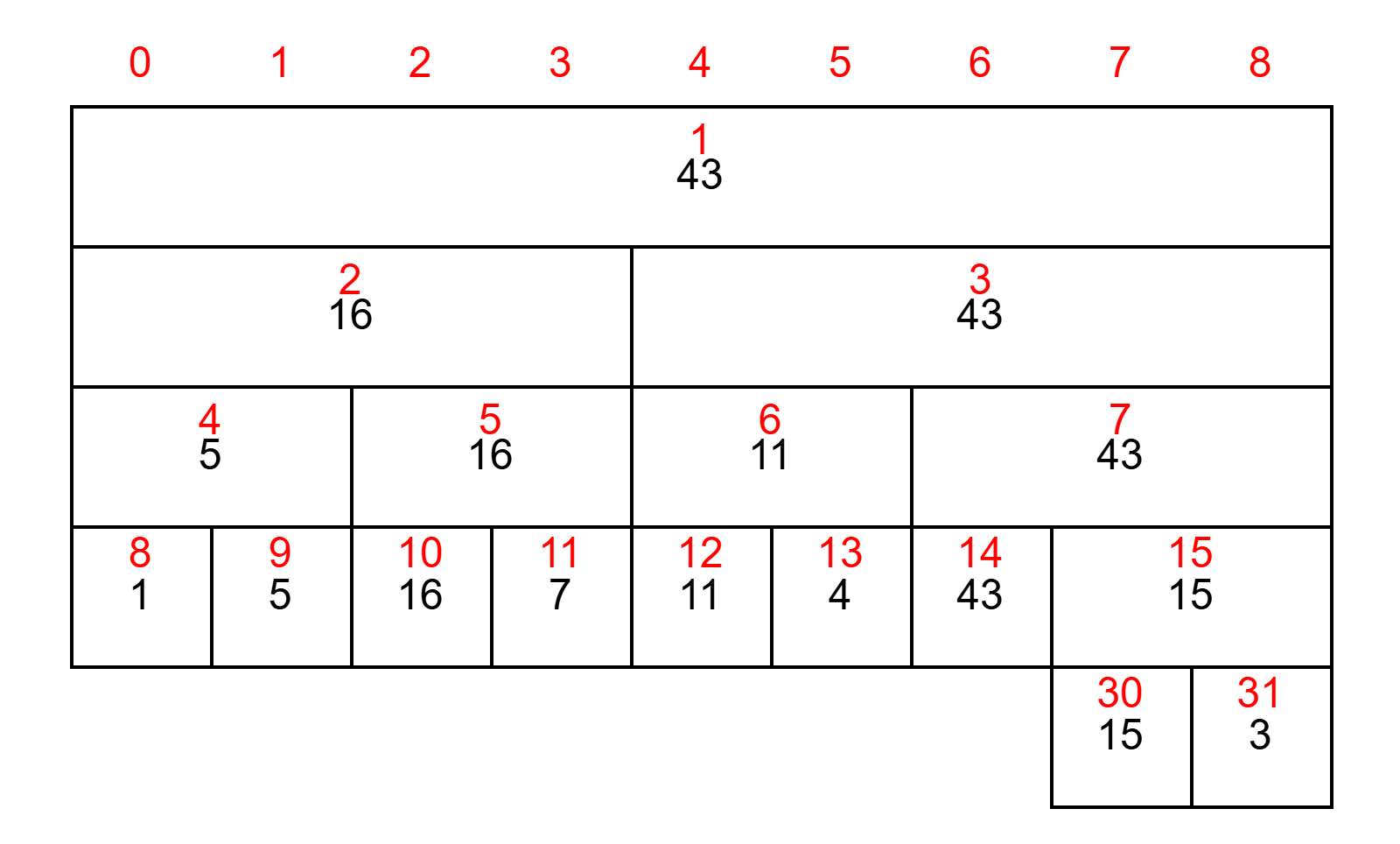 --> 假設當前陣列是a = [ 1, 5, 16, 7, 11, 4, 43, 15, 3] 當前節點$i$有區間$[l,r]$ 代表的是區間$[l,r]$內的最大值 ---- ## 建樹 可以發現葉節點的區間長度皆為1，以區間長度等於1為結束遞迴的條件 有 左閉右開 / 左閉右閉 許多版本 這裡的code是左閉右開 ```cpp! #define cl(x) (x << 1) #define cr(x) ((x << 1) | 1) void build(int id,int l,int r){ if (r - l == 1){ info[id] = arr[l]; return ; } int mid = (l+r) >> 1; build(cl(id), l, mid); build(cr(id), mid, r); // 合併兩個區間 info[id] = max(info[cl(id)], info[cr(id)]); } ``` ---- ### 區間查詢 假設要查詢區間 [2, 6]  就是拿這三塊去merge ---- 可以簡單分成 3 種情況 - 當前區間被查詢區間包含 - 當前區間和查詢區間不相交 - 前兩種以外的情況（有相交） 不相交的話當前區間資訊沒有意義 包含的話不用繼續遞歸他的子節點 其他情況要繼續遞歸 ``` cpp! inline i32 cl(i32 x) { return x << 1; } inline i32 cr(i32 x) { return (x << 1) | 1; } int rangeQuery(i32 p, i32 l, i32 r, i32 x, i32 y) { if (l >= y || r <= x) return -inf; // 不相交 回傳極小值，對答案沒有貢獻 if (l >= x && r <= y) return info[p]; // 包含 i32 m = (l + r) >> 1; return max(rangeQuery(cl(p), l, m, x, y), rangeQuery(cr(p), m, r, x, y)); } ``` ---- ### 單點修改 如果要修改 [7] 綠色的部分都有可能被修改  ---- 我們先遞歸找到最底下長度為 1 那個要修改的點 修改那個點，然後往上合併更新他的父節點 ```cpp! inline i32 cl(i32 x) { return x << 1; } inline i32 cr(i32 x) { return (x << 1) | 1; } void modify(i32 p, i32 l, i32 r, i32 x, int v) { if (r - l == 1) { // info[p] = v; return; } i32 m = (l + r) >> 1; if (x < m) modify(cl(p), l, m, x, v); else modify(cr(p), m, r, x, v); info[p] = max(info[cl(p)], info[cr(p)]); } ``` ---- ## 區間求總和 給一個長度為$n$的陣列$a$，有$q$個操作，分為以下2種： - $1$ $l$ $r$ 詢問$[l,r]$區間的總和 - $2$ $x$ $v$ 把$a_x$設為$v$ $1 \le n,q \le 2*10^5$ ---- 可以發現就只是區間求最大值換成區間求總和 可以建出區間求總和的線段樹  arr = [1, 5, 16, 7, 11, 4, 43, 15, 3] ---- 如果要查區間 [2, 6] 總和 就會是這三個區間加在一起  ---- 會發現不一樣的地方只有合併兩個小區間的部分 ``` cpp! info[p] = max(info[cl(p)], info[cr(p)]); // 維護區間最大 info[p] = info[cl(p)] + info[cr(p)]; // 維護區間總和 ``` ---- ### 區間查詢 ```cpp! int rangeQuery(i32 p, i32 l, i32 r, i32 x, i32 y) { if (l >= y || r <= x) return 0; // 不相交 回傳0 （對總和沒有貢獻） if (l >= x && r <= y) return info[p]; // 包含 i32 m = (l + r) >> 1; return rangeQuery(cl(p), l, m, x, y) + rangeQuery(cr(p), m, r, x, y)); } ``` ---- ### 單點修改 ``` cpp! void modify(i32 p, i32 l, i32 r, i32 x, int v) { if (r - l == 1) { info[p] = v; return; } i32 m = (l + r) >> 1; if (x < m) modify(cl(p), l, m, x, v); else modify(cr(p), m, r, x, v); info[p] = info[cl(p)] + info[cr(p)]; } ``` ---- 因為線段樹要維護的資料不一定只有一個數字 所以實作的時候可以用struct來存你需要的資料 細節可以看完整程式碼 ---- ### 完整程式碼 [左閉右開](https://github.com/asd7766zxc/Miaotomata_CodeBook/blob/main/dataStructure/new_segtree%E5%96%AE%E9%BB%9E.cpp) --- ## 休息一下，等等有一堆例題講解！ --- ## 例題：[正負交替](https://codeforces.com/edu/course/2/lesson/4/4/practice/contest/274684/problem/A) 給一個長度為$n$的陣列$a$，有$q$個操作，分為以下2種： - $1$ $x$ $v$ 把$a_x$設為$v$ - $2$ $l$ $r$ 詢問$a_l-a_{l+1}+a_{l+2}...\pm a_{r}$的總和 ---- 可以發現要查詢的左界都是正的 ---- ``` 0 1 2 3 4 5 6 7 8 9 + - + - + - + - + - - + - + - + - + - + ``` 可以用兩個線段樹 根據不同的$l$再去判斷要用哪顆線段樹去查詢就好了 ---- ## 例題：[區間不同數字數量](https://codeforces.com/edu/course/2/lesson/4/4/practice/contest/274684/problem/D) 給一個長度為$n$的陣列$a$，$q$筆操作，有以下兩種操作 - $1$ $l$ $r$ 詢問區間$[l,r]$內有幾種不同的數字 - $2$ $x$ $v$ 把$a_x$設為$v$ $1 \le n,q \le 10^5$ $1 \le a_i \le 40$ ---- 因為數值不大 每一個節點開一個bitset 合並的時候用or就好 ---- ## 例題：[區間最大連續和](https://codeforces.com/edu/course/2/lesson/4/2/practice/contest/273278/problem/A) 給一個長度為$n$的陣列$a$，有$q$個操作，分為以下2種： - $1$ $l$ $r$ 詢問$[l,r]$的區間最大連續和 - $2$ $x$ $v$ 把$a_x$設為$v$ $1 \le n,q \le 2*10^5$ ---- 前面說過只要兩個區間的資訊可以合並成大區間的資訊就可以使用線段樹 怎麼維護最大連續和？ ---- 可以發現要維護最大連續和需要最大前綴和最大後綴 維護最大連續和又需要區間總和 ----  L.sufix就是左子樹的後綴最大 (以此類推 sum = L.sum + R.sum prefix = max(L.sum + R.prefix, L.prefix) sufix = max(R.sufix, R.sum + L.sufix) ans = max(L.ans, R.ans, L.sufix + R.prefix) --- ## 線段樹上二分 由於線段樹上每個大區間都會二分成兩個小區間 因此可以做一些二分搜之類的操作 ---- ## 例題：[第k個1](https://codeforces.com/edu/course/2/lesson/4/2/practice/contest/273278/problem/B) 長度為$n$的陣列$a$內只有0和1兩種數字，$q$筆操作 分為以下兩種： - $1$ $k$ 詢問陣列從左往右數來第$k$個1在哪個index - $2$ $x$ 把$a_x$的1變0或是0變1 $1 \le n,q \le 10^5$ ---- 假設陣列為 arr = [1, 0, 1, 0, 1, 0, 0, 1, 1] 可以以建區間總和的線段樹來做 這裡假設要查第三個1在哪裡 <!--  --> <center> <img src="https://hackmd.io/_uploads/r1RpMdPh1e.png" width="700px"> </center> ---- 藍色數字代表要查當前區間的第幾個 1. 左邊只有二個1，所以找右子區間(3)的第一個1 1. 左邊有一個1，所以往左邊找左子區間(6)的第一個1 1. 左邊有一個1，所以往左邊找左子區間(12)的第一個1 2. 發現這個區間長度為1，代表已經找到了 <center> <img src="https://hackmd.io/_uploads/Syu4Sdwhkx.png" width="700px"> </center> <!--  --> ---- ## 例題：[至少大於K的第一個元素](https://codeforces.com/edu/course/2/lesson/4/2/practice/contest/273278/problem/C) 給一個長度為$n$的陣列$a$，$q$筆操作，有以下兩種操作 - $1$ $k$ 詢問陣列從左往右數來第一個大於$k$的數字的index - $2$ $x$ $v$ 把$a_x$設為$v$ $1 \le n,q \le 10^5$ ---- 可以發現要維護區間最大，才能知道這個區間有沒有大於K的元素 其他跟上一題一樣 --- 來練習._. [題目](https://vjudge.net/contest/702395)