<style> .reveal .slides { text-align: left; font-size:28px; } </style> ## Classic Flow Problems - 二分圖 - 最大獨立集 - 最小點覆蓋 - 最大權獨立集 - 最小路徑覆蓋 - 最多不相交路徑 - 最大權閉合子圖 - 分層圖 flow - 平面圖最小割 --- ### 二分圖最小點覆蓋（Minimum Vertex Cover） König Theorem 最小點覆蓋：選出最少的點，滿足每條邊至少有一個端點被選。 二分圖中，最小點覆蓋 = 最大匹配。 ---- ### 二分圖最大獨立集 (Maximum Independent Set ) 最大獨立集：選出最多的點，滿足兩兩之間沒有邊相連。 因為在最小點覆蓋中，任一條邊都被至少選了一個頂點，所以對於其點集的補集，任一條邊都被至多選了一個頂點，所以不存在邊連接兩個點集中的點，且該點集最大。 因此二分圖中，最大獨立集 = n - 最小點覆蓋。 ---- ### [No Prime Sum](https://vjudge.net/problem/CSAcademy-no-prime-sum) 給 $n$ 個相異正整數，要刪除最少的整數，使得數字兩兩相加不能為質數 - $2\le n\le 2000$ - $1\le a_i\le 10^5$  ---- 分 case 時間 - 奇數 + 奇數 = 偶數 - 偶數 + 偶數 = 偶數 - 奇數 + 偶數 = 奇數 (可能為質數) 由於所有數字都相異，因此相加若為偶數則 $> 2$ ---- 因此把所有可能相加為質數的 pair 連邊，會發現都是奇數和偶數連邊 形成一張二分圖，偶數一群，奇數一群 偶數和奇數之間有連邊 ---- 目標為相加不能為質數，也就是連邊的點對最多只能選一個留下來 $\to$ 二分圖上最大獨立集。 ---- ## 求解 根據定理，最大獨立集 = n - 最小點覆蓋 跑二分圖最大匹配後，要找出要刪除哪些 ---- 使用 dinic 跑完後，從源點 $S$ 開始跑殘餘流量圖 ([code](https://hackmd.io/@LeeShoWhaodian/2024flow#/4/4)) 跟源點 $S$ 同側的子圖有 2, 5, 11 和匯點 $T$ 同側的子圖有 4, 7  而最大獨立集的點為左側(奇數)被走到和右側(偶數)沒被走到的點 也就是 5, 11, 4 即為其中一組最大獨立集 ---- ## 二分圖最大權獨立集 (Maximum Weighted Independent Set ) ---- ## 方格取數問題 有一個 $m\times n$ $(1\le n, m\le 30)$ 格的棋盤，每格中都有一個正整數。 要從方格中取數，使得取的數字皆沒有共邊，且取出的數的總和最大。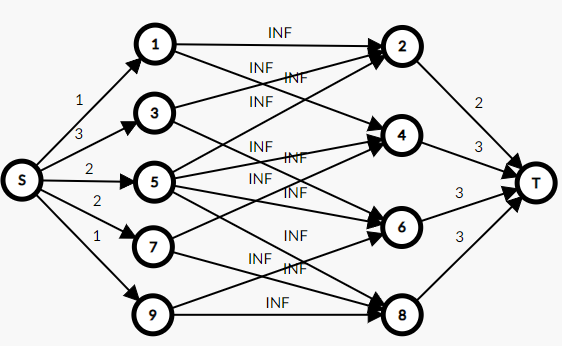  選 (0, 1), (1, 0), (1, 2), (2, 1) 2+3+3+3=11 ---- 方格上取的數字皆沒有共邊 $\to$ 二分圖獨立集 (奇偶分群) 取出的數的總和最大 $\to$ 最大權 $\to$ 二分圖帶權最大獨立集 ---- 嘗試把二分圖畫出來 把相鄰的格子連邊流量設 INF 起點連到奇點，權重為奇點上的權重 偶點連到匯點，權重為奇點上的權重  ---- ### 目標 --- 選的點不能相鄰 要使得選的點皆不相鄰，等價於至少有一個到源點或匯點的邊要割掉。 （割中間流量為無窮大的邊，因此不選）  要選權重總和最少的邊集合割掉，使得源點與匯點不連通 $\to$ 最小割 ---- 根據定理 最小割 = 最大流 因此把全部點的總和 減去 建出來的圖的最大流即為答案 --- ## 最小路徑覆蓋 (Minimum Path Cover) 給定一張**有向無環圖** $(n \le 200, m \le 6000)$ 求出最少需要幾條路徑，可以使得每個點都剛好在一條路徑上  {1 $\to$ 5 $\to$ 4}, {6 $\to$ 7 $\to$ 8}, {2 $\to$ 3} ---- ## 作法 把每個點拆成 **入點** 和 **出點**，轉化為二分圖 原圖頂點數 減去 二分圖最大匹配數 即為最少路徑覆蓋數量 <div style="position:absolute; right: 70%;top:90%;">  </div> <div style="position: absolute; right: 55%;top:150%;"> $\to$ </div> <div style="position:absolute; right: 10%; top:90%;">  </div> ---- 匹配成功的點對 $(i, j)$，即為對於 $i$ 連到 $j$ 的邊接起來 <div style="position:absolute; right: 70%;top:90%;">  </div> <div style="position: absolute; right: 55%;top:280%;"> $\to$ </div> <div style="position:absolute; right: 10%; top:90%;">  </div> --- ## 最長遞增子序列 給出一段序列 $a$ $(n \le 500 )$，讓你求出： 1.最長遞增子序列的長度 2.最多同時可以取出幾個最長遞增子序列 3.如果第一個元素和最後一個元素可以用無數次，最長遞增子序列可以取出幾個 ---- ## 最長遞增子序列的長度 這個問題可以直接 DP 解 以第 $i$ 個為結尾的最長遞增子序列長度 $dp[i]$ ---- ## 最多同時可以取出幾個 LIS ### 建模 確保每個點最多只能拿一次 先拆點，分成入點 $(i)$ 與出點 $(i')$，入點連到出點流量為 $1$ 源點連到所有 $i \in$ (dp[i] = 1)，addEdge$(S, i, 1)$ 對於所有 $i \in$(dp[i] = 最長長度)的連到匯點，addEdge$(i', T, 1)$ 對於所有 $(i, j)$ 符合$a[i]<a[j] \wedge dp[i]+1=dp[j]$ 建邊 點 $i$ 的出點連出去到 點 $j$ 的入點，addEdge$(i', j, 1)$ ---- ## 建模 ` a = [2, 4, 1, 3]` `dp = [1, 2, 1, 2]`  ---- ### 如果第一個元素和最後一個元素可以用無數次，最長遞增子序列可以取出幾個 想法：把點 1、點 N 分別當作第二個源點與第二個匯點 作法：把點 1 連到的邊與點 N 連出去的邊流量改為 INF 即可  --- ## 最大權閉合子圖 ### Maximum Closure Problem ---- ## 太空飛行計劃問題 <div style="font-size:30px;"> 有一個實驗集合 $E$ = { $E_1,E_2,...,E_m$ } 還有實驗儀器的集合 $I$ = { $I_1,I_2,...,I_n$ } $n,m \le 50$ 實驗 $E_j$ 需要用到的儀器是 $I$ 的子集 $R \in I$。 使用儀器 $I_k$ 的費用為 $c_k$ 元 實驗 $E_j$ 能獲得 $p_j$ 元 W 教授的任務是找出一個有效算法，確定在一次太空飛行中要進行哪些實驗並因此而配置哪些儀器才能使太空飛行的淨收益最大。 淨收益是指進行實驗所獲得的收入與配置儀器的費用的差額。 </div> ---- ## 建模 源點連到所有實驗，流量為得到的錢 $p_j$ 每個實驗儀器連到匯點，流量為使用費用 $c_i$ 每個實驗連到所有儀器，流量為 $\infty$ ---- ## 最小割 考慮割掉某個實驗，以下面為例 實驗 1 可以獲得 100 元 需要設備 A ( 成本 40 ) & 設備 B ( 成本 80 )  最小割出現割在實驗的地方 ( 實驗獲利 $\le$ 總成本 ) 實驗是收益，而收益不夠支出 因此 **不進行該實驗**。 ---- ## 最小割 考慮割掉某個設備，以下面為例 實驗 1 可以獲得 100 元 需要設備 A ( 成本 40 ) & 設備 B ( 成本 8 )  最小割出現割在設備的地方 ( 實驗獲利 > 總成本 ) 設備是花費，而支出少於收益 因此 **使用該儀器**。 ---- ## 轉換 <div style="font-size:30px;"> 我們得到的最小割集合為 { **不進行的實驗總收益**, **使用的儀器總成本** } 想得到最大收益為 **進行的實驗總收益** - **使用的儀器總成本** 要得到上面的東西為 全部實驗總收益 - 最小割 = ( **進行的實驗總收益** + **不進行的實驗總收益** ) - ( **不進行的實驗總收益** + **使用的儀器總成本** ) = **進行的實驗總收益** - **使用的儀器總成本** = 答案 在根據最小割 = 最大流，直接跑最大流即為答案。 </div> ---- ## 最大閉包(最大權閉合子圖) 給定一張有向圖，有點權且可正可負 要找到某個子圖，滿足以下： - 對於所有邊 $(u, v)$，若點 $u$ 在子圖中，則點 $v$ 也在子圖中 - 使得選的子圖點權總和最大 ---- ## 建模 源點連到所有正權點流量為點權 所有負權點連到匯點流量為點權(絕對值) 所有圖上的邊權重為 $\infty$ <div style="position:absolute; right: 60%;top:90%;">  </div> <div style="position:absolute; right: 50%;top:135%;"> $\to$ </div> <div style="position:absolute; right: 10%;top:90%;">  </div> 建出來的圖即可轉換為上一題同一個問題 <!-- ## 最大密度子圖 給你一個長度為 $n$ $(n\le 100)$的序列 $T$，$S$ 為 $T$ 的任意子序列 inv(S)表示子序列 S 中的逆序對數數量 len(S) 表示S的長度，求出$\frac{inv(S)}{len(S)}$ 的最大值。 ## 題目轉換 (最大密度子圖) 給你一張圖 求某個子圖使得 $\frac{m}{n}$ 最大化 --> --- ## 分層圖 flow ---- ## 星際轉移問題 有 $k$ $(1 \le k \le 50)$個人要從地球到月球， 其中有 $n$ $(1\le n \le 13)$ 個太空站， 每個太空站可以容納無限多的人 有 $m$ $(1 \le m \le 20)$個太空船在一些太空站之間週期性的來回 每個太空船可以容納 $h_i$ 個人 並且從當前太空站到下一個所需時間為 1 秒 問你是否能把所有人送到月球，或者輸出無解 ----  有 1 人要載 A 太空船可以載 1 人, B 太空船可以載 1 人 | 時間 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | --- | - | - | - | - | - | - | - | - | - | | A太空船位置 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | | B太空船位置 | 1 | 2 | -1 | 1 | 2 | -1 | 1 | 2 | -1 | 所需時間為 5 ---- 網路流? 但好像沒辦法建圖? 觀察測資大小 - $k$ $(1 \le k \le 50)$ 個人 - $n$ $(1\le n \le 13)$ 個太空站 - $m$ $(1 \le m \le 20)$個太空船 會發現最差的情況下只需要最多 $n^2\cdot k$ 天把所有人載完 ---- 對於所有太空站在所有時間點都變成一個節點 把圖建成以下  對於每個太空船每天在的位置建邊到下一天的位置流量為 $H_i$ ---- 每個人也可以第 $d$ 天待在同一個太空站待到第 $d+1$ 天 流量為無限大 (太空站可以容納無限多個人)  ---- 並且把 flow 的 源點連到地球的第 0 天的節點流量為總人數 $k$ 匯點從每天的月球連過去流量為無限大  ---- <div style="font-size:30px"> 對於建完的圖，我們可以二分搜總天數 $d$，建出 $d$ 天的分層圖 如果最大流流量為 $k$ 代表我們可以用 $d$ 天，把這 $k$ 個人運送到月球  </div> --- ## 平面圖最小割 (Min Cut in a Planar Graph) 結論：平面圖最小割 = 對偶圖最短路 平面圖為沒有邊相交的圖 ---- ### 例題：BZOJ1001 --- 狼抓兔子 給一張 $N\times M$ $(1\le N, M\le 1000)$ 的網格圖 一開始有無限多隻兔子在左下角 (1, 1)，而有野狼要抓他們 所以要跑到右上角 $(N, M)$ 的位置 而每次可以從 (i, j) 跑到 (i+1, j), (i, j+1), (i+1, j+1) 的位置 並且每條道路有流量上限，想問你在不超過上限的情況下最多有幾隻兔子可以到右上角 ---- 給一張 $N\times M$ $(1\le N, M\le 1000)$ 的網格圖 一開始有無限多隻兔子在左下角 (1, 1)，而有野狼要抓他們 要跑到右上角 $(N, M)$ 的位置  ---- $N\times M$ $(1\le N, M\le 1000)$ 很明顯這題是一個平面圖上的最大流問題， 但 $N\times M$ 最大會到 1e6 直接跑 flow 會 TLE ---- ## 平面圖 平面圖是可以畫在平面上並且使得不同的邊可以互不交疊的圖  ---- ## 平面圖的對偶圖 對於平面圖 G 的對偶圖 G*，其 G 的每個面皆為對偶圖 G* 的點， G 中的每條邊 e ，為 G* 連接兩個面的邊 e* 而如果 G* 中一條邊 e* 連接的為同一個平面，則此條邊為自環  ---- 根據定理，平面圖最小割 = 對偶圖最短路  ---- 把每個平面當成一個點，而兩個點有連一條雙向邊為兩個平面用一條邊隔開 而兩個點之間的邊權即為隔開的那條邊的權重 而起始點從原本左下右上變成左上右下  ---- 好好地建邊 跑 dijkstra 即可把複雜度從 $O(MN^2)$ 變成 $O(M\log N)$  --- Flow 的建模跟 DP 想轉移式一樣，多看多練習就能熟悉 :poop: 很多經典的轉換題目都是建邊跑最大流為答案 或者 總和-最大流是答案 可以試著好好建圖觀察並證明 而如果你是隊上負責建模的應該要去好好刷以下題單 [網路流 24 題](https://loj.ac/p?tagIds=30) 大部分的網路流的問題都是經典問題的轉換 好好寫完就能成為 flow 的神了 m\(_ \_\)m ---- ### Question Time and Practice [Homework Link](https://vjudge.net/contest/654756)