<style> .reveal .slides { text-align: left; font-size:35px } </style> ## Tree & Disjoint Set 11/10 preTrain --- ## Table of Contents - Tree 簡介 - 複習: 樹的定義 - 有根樹 - 生成樹 - 樹的性質 - 樹上遍歷 - BFS - DFS 與性質 ---- - 經典樹上演算法 - 子樹大小 - 找樹高 - 找樹的深度 - 找樹的直徑 - 找樹的重心 - 常見的樹狀資料結構 - Disjoint Set (Union-Find) - 經典 DSU 例題 - 找最小生成樹 : Kruskal 演算法 --- ## Tree 簡介 ---- ### 複習: 樹的定義 常見有四種定義方式，**他們其實都一樣** 1. 連通無環圖 2. 連通且邊數為 $n-1$ 的圖 3. 無環且邊數為 $n-1$ 的圖 4. 無自環且任兩點僅存在唯一路徑的圖 ---- ### 哪裡會看到樹? - 資料結構 - 演算法 - 賽局 - 作業系統 - 編譯器 / 形式語言 tree 無所不在，所以我們沒有理由不學 tree <!-- .element: class="fragment" data-fragment-index="1" --> ---- 以下這個就是樹  ---- ### 有根樹 我們可以取一點當作根，然後把其他節點都掛在根底下 如此一來節點之間就會出現祖先與後代的關係  ---- ### 有根樹的名詞解釋 給定節點 $x$，與根 $r$ - 祖先 : 從 $x$ 到 $r$ 的所有節點們 - 後代 : 從 $x$ 遠離 $r$ 的所有節點們 這些定義有時有包含 $x$ 本人，有時沒有 <!-- .element: class="fragment" data-fragment-index="1" --> ---- 給定節點 $x$，與根 $r$ - 父節點 : 與 $x$ 相鄰且更靠近 $r$ 的點 - 子節點 : 與 $x$ 相鄰且更遠離 $r$ 的點 ---- ### 子樹 (subtree) 刪掉與父親相連的邊後，該節點所在的子圖  ---- ### 生成樹 (spanning tree) 由於樹是「最小連通子圖」 所以我們常會想在圖中找到一棵樹 定義 : 圖 $G$ 取出一棵樹 $T$ 使 $V(T)=V(G)$，則 $T$ 為 $G$ 的生成樹 ---- 右圖是左圖的生成樹 :evergreen_tree: <div style="position: absolute; right: 0%; top:100%;">  </div> <div style="position: absolute; left: 0%; top:100%;">  </div> ---- 題外話 : 上堂課說的 DFS / BFS 也會形成生成樹喔 ---- ### 有根樹的性質 - 兩點距離 : 兩點之間的邊數 - 節點深度 : 從點到根的距離 - 子樹高度 : 子樹從根到最遠葉子的距離 - 直徑 : 樹中最長的距離 - 重心 : 等等再說 --- ## 樹上遍歷 ---- 由於每個節點只會有一個父節點 相較於一般圖上遍歷 可以不用 $\text{vis[ ]}$ 紀錄節點是否走過 沒有環所以就不會有重複走的問題 ---- ### 樹上 BFS 可以用 pair 維護當前節點與父節點 ```cpp= void bfs(int s){ queue<pair<int,int>> q; q.push(make_pair(s, 0)); while(!q.empty()){ auto [x, y] = q.front(); q.pop(); for(int i : g[x]) if(i != y) q.push(make_pair(i, x)); } } ``` ---- ### 樹上 DFS 函數多傳一個參數就可以維護父節點 ```cpp= void dfs(int x, int father){ for(int i : edge[x]){ if(i != father) dfs(i, x); } } ``` ----  ---- ### 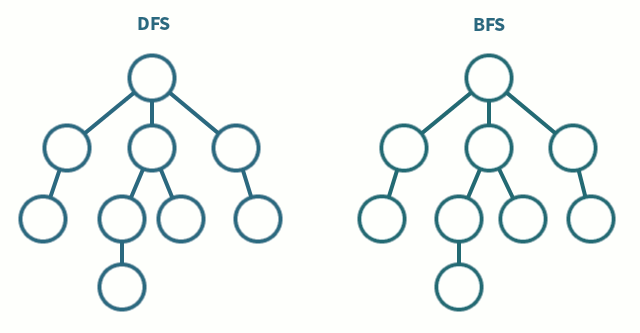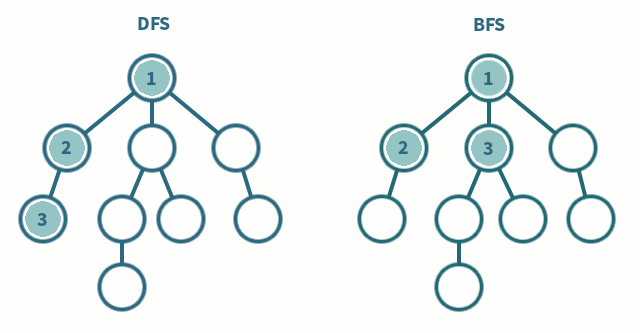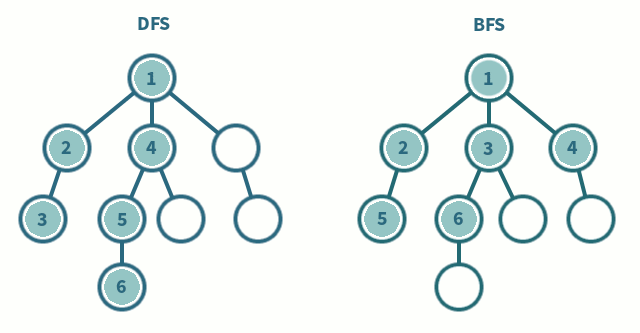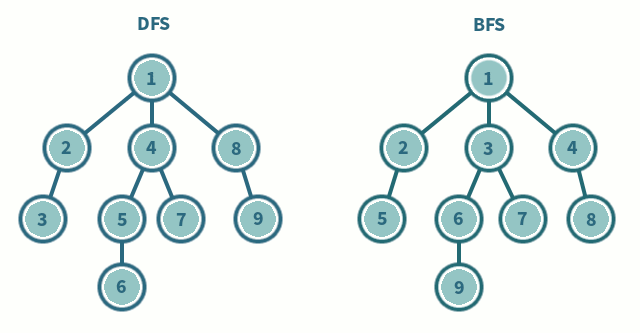DFS 的名詞 DFS 時，我們可以把每個點分成三個狀態 - 白點 : 尚未被發現 - 灰點 : 被發現但後代還沒找完 - 黑點 : 被發現且後代都找完 ---- 小提醒 : 在樹上做處理時要想清楚，節點要在什麼狀態時做處理 - 剛被發現時處理 : 灰點 - 子樹處理完再處理 : 黑點 --- ## 經典樹上演算法 ---- ### 子樹大小 求出一棵有根樹中 $x$ 的子樹大小 (節點數量) - 一個點的子樹大小為 $1+\sum_{i}\text{sz}[子樹_i]$ - 葉節點的子樹大小為 $1$ ```cpp= int sz[MXN]; int dfs(int x, int father) { sz[x] = 1; for(int i : edge[x]){ if(i != father){ // 先 dfs 算子樹的結果, 算出後再加入 sz[x] sz[x] += dfs(i, x); // 此時 i 已經是黑點 (拜訪完所有後代) } } return sz[x]; } ``` ----  ---- ### 找樹的深度 求出一棵有根樹每個節點的深度 - 子節點深度為父節點深度 $+1$ (或邊權) - 根節點的深度為 $0$ (或 $1$，視題目要求) ```cpp= int d[MXN]; void dfs(int x, int father){ for(int i : edge[x]){ if(i != father){ // 在 i 還是灰點時就處理 d[i] = d[x] + 1; dfs(i, x); } } } ``` ----  ---- ### 找樹高 求出一棵有根樹每個節點的高度 - 一個點的高度為所有子節點中，高度最高者 $+1$ - 葉節點的高度為 $0$ (或 $1$，視題目要求) ```cpp= void dfs(int x, int father){ h[x] = 0; for(int i : edge[x]){ if(i != father){ dfs(i, x); h[x] = max(h[x], h[i] + 1); } } } ``` ----  ---- ### 找樹的[直徑](https://cses.fi/problemset/task/1131) (方法 1) 求出一棵樹最遠兩點的距離 - 先任選一點作為根，將其視作有根樹 - 考慮分治法：直徑可能 1. 經過根節點，也就是前兩高度 2. 不經過根節點，也就是在某棵子樹上，因此遞迴計算子樹的答案再取$\max$ - 兩者再取$\max$即為答案 ---- ```cpp int ans; int dfs(int x, int father){ int mh1 = 0, mh2 = 0, cur; for(int i : edge[x]){ if(i != father){ cur = dfs(i,x); if(cur > mh1) mh2 = mh1, mh1 = cur; else if(cur > mh2) mh2 = cur; } } ans = max(ans, mh1 + mh2); return mh1 + 1; } ``` ---- ### 找樹的[直徑](https://cses.fi/problemset/task/1131) (方法 2) 1. 任選一點開始做 DFS，找出最遠(深)的點，記為 $\text{mx}$ 2. 從 $\text{mx}$ 開始做 DFS，其與最遠點的距離即為直徑 (也就是第二次DFS的高度$+1$) ---- ```cpp int md, mx; void dfs(int x, int father, int d = 0){ if(d > md) md = d, mx = x; for(int i : edge[x]){ if(i != father) dfs(i, x, d + 1); } } int find_diameter(){ md = -1; dfs(0, 0); md = -1; dfs(mx, mx); return md; } ``` ---- ### 樹重心 求一棵樹的重心，以下是重心的定義： - 如果在樹中選擇某個節點並刪除，這棵樹將分為若干棵子樹，統計子樹節點數並記錄最大值。取遍樹上所有節點，使此最大值取到最小的節點稱為整棵樹的重心。 ---- 簡單來說就是一個演算法式的定義，可以整理成以下 我們對所有節點 $x\in V$ 執行以下操作 $f(x)$ : 1. 刪除節點 $x$，刪除後會出現森林 2. 統計每棵樹節點數，並記錄最大值 $m$ 3. $f(x)$ 的值即為 $m$ 樹的重心為 $c$，$f(c)=\begin{split}\min_{x\in V}f(x)\end{split}$ ---- 以這圖為例： <div style="position: absolute; left: 60%; top:60%;">  </div> 砍掉點 $1$，剩下的最大子樹為 $2$-$5$-$6$-$7$，$\text{sz}$ 為 $4$ 砍掉點 $2$，剩下的最大子樹為 $1$-$3$-$4$，$\text{sz}$ 為 $3$ 砍掉點 $5$，剩下的最大子樹為 $1$-$2$-$3$-$4$-$6$，$\text{sz}$ 為 $5$ 所以樹重心為節點 $2$ ---- 樹的重心也不一定唯一 右圖樹重心為 $1$ 和 $2$ <div style="position: absolute; right: 20%; top:0%;">  </div> ---- <div style="position: absolute; left: 0%; top:0%;"> ### 怎麼找樹重心 關鍵的地方在於，要找到刪掉某個點後， 剩下最大的子樹的 $\text{sz}$ 為多少 - 假設要刪掉點 $x$ - 則要去拿 $x$ 的所有的子樹 $\text{sz}$ - 以及 $x$ 往上的樹的 $\text{sz}$ 假設要刪掉 $2$ ，除了要檢查 $5$ 和 $6$ 的子樹大小， 還要檢查 $2$ 上方的子樹大小，大小為 $(n - (2的子樹大小) )$ </div> <div style="position: absolute; right: 10%; top:0%;">  </div> ---- ### 找樹的[重心](https://cses.fi/problemset/task/2079) (方法 1) 1. 預處理 $\text{sz[ ]}$ 2. 探索每個點 - 算最大子樹大小 - 紀錄答案 ---- 1. 預處理 (跟前面找子樹大小相同) ```cpp= int sz[MXN]; int dfs(int x, int father) { sz[x] = 1; for(int i : edge[x]){ if(i != father) sz[x] += dfs(i, x); } return sz[x]; } ``` ---- 2. 探索每個點 (算最大子樹大小 + 紀錄答案) ```cpp= int cen_sz = inf, cen = -1; void find_cen(int x, int father){ // 找孩子 sz int mx_sz = 0; for(int i : edge[x]){ if(i == father) continue; mx_sz = max(mx_sz, sz[i]); } // 找上方的樹 sz mx_sz = max(mx_sz, n - sz[x]); // 紀錄答案 if(cen_sz > mx_sz){ cen_sz = mx_sz; cen = x; } //算完就往下遞迴算 for(int i : edge[x]){ if(i == father) continue; find_cen(i, x); } } ``` 這樣就找到重心了 ---- 另外還有一個名詞叫[樹中心](https://www.tutorialspoint.com/centers-of-a-tree)，跟樹重心類似， 只是判斷的條件從 sz(大小) 變成 depth(深度) ---- ### 找樹的[重心](https://cses.fi/problemset/task/2079) (方法 2) 先看個定理 : 將樹以 $c$ 為根， $c$ 為重心若且唯若對任一子樹 $T_i$ 節點數 $|T_i|$ 都有 $|T_i| \;\le\; \bigl\lfloor\tfrac{n}{2}\bigr\rfloor$ ---- $|T_i| \;\le\; \bigl\lfloor\tfrac{n}{2}\bigr\rfloor$  ---- 所以只要檢查每棵子樹 (加上頭上那個樹) 是不是都 $\le \bigl\lfloor\frac{n}{2}\bigr\rfloor$ ```cpp= int cent; // 這就是重心 void dfs(int u, int pre){ sz[u] = 1; int mx = 0; for(int &v : g[u]){ if(v == pre) continue; dfs(v, u); sz[u] += sz[v]; // 此時 v 已是黑點 mx = max(mx, sz[v]); } mx = max(mx, n - sz[u]); if(mx <= n / 2) cent = u; } ``` 這種方法直接不需要預處理了，可以跟子樹大小寫在一起 ---- 再複習一下 我們對所有節點 $x\in V$ 執行以下操作 $f(x)$ : 1. 刪除節點 $x$，刪除後會出現森林 2. 統計每棵樹節點數，並記錄最大值 $m$ 3. $f(x)$ 的值即為 $m$ 樹的重心為 $c$，$f(c)=\begin{split}\min_{x\in V}f(x)\end{split}$ ---- ### 找樹的重心 (方法 3) <div style="position: absolute; right: 0%; top:0%;">  </div> 再來看看一個定理 : 從任意點 $x$ 沿著重心 $c$ 方向移動，則 - $f(x)$ 非遞增 - 在到達 $c$ 時達到最小值 ---- 這可以推得 : 令 $r$ 為根，則若存在 $|T_i| \ge\bigl\lfloor\tfrac{n}{2}\bigr\rfloor$，則重心存在於子樹 $T_i$， 所以直接找這棵樹 $T_i$ 即可 ---- ```cpp= int dfs(int u, int pre){ // 這個先預處理 sz[u] = 1; for(int v : g[u]){ if(v == pre) continue; sz[u] += dfs(v, u); } return sz[u]; } int get_cent(int u, int pre){ for(int v : g[u]){ if(v != pre && sz[v] > n / 2) // 這條件代表重心在 v 的子樹 return get_cent(v, u); } return u; // 每個子樹都 <= (n / 2)，則符合重心定義 } dfs(1, 0); ans = get_cent(1, 0); ``` 這方法或許可以壓掉一些常數，因為可能不會找完整棵樹 有個技巧叫重心剖分就要用這個方法 ---- 三種找樹重心的方法[等價的證明](https://hackmd.io/@ShanC/special-vertices-on-tree#重心-Centroid) 可以自己翻來看看，看不懂就畫畫看圖 --- ## Disjoint Set (Union-Find) #### 併查集、DSU ---- ### DSU 簡介 併查集是一種有向有根的樹狀結構，專門處理集合問題， 主要有以下兩個操作 : - 查詢元素所在集合(find) - 合併兩個集合(union) ---- ### 小觀察 樹上每個節點只會有一個父節點 $\Rightarrow$ 只需要一個陣列就可以存一整棵樹 ---- ### 儲存資料 併查集需要用一個長度為 $n$ 的陣列 $\text{f[ ]}$， $\text{f}[i]$ 值為第 $i$ 個節點的父節點編號 ```cpp= int f[n]; f[3] // 節點 3 的父節點編號 f[5] // 節點 5 的父節點編號 ``` ---- ### 根節點 如果一個點為根節點，他的父節點為自己 $(\text{f}[x] == x)$ 以下圖為例， $1$、$6$ 為根節點  ---- ### 判斷集合 定義兩個相異元素如果屬於同一個集合，則兩個元素會在並查集的同一棵樹上 ---- 如何判斷在同一棵樹上? ---- ### find 函數 find 函數會找到某個節點 $x$ 的根節點 如果兩個點的根節點相同，代表在同一棵樹上， 也就是屬於同一個集合 ``` find(x) == find(y); ``` 則 x 與 y 所屬同一個集合 ---- ### find 函數 ```cpp= int find(int x){ if (x == f[x]) // 如果當前節點為 f[x] == x return x; // 則為根節點 return find(f[x]); } ``` ---- ### union 函數 有兩個節點 $a, b$ 所在的集合想要合併成一個集合 : 1. 找到兩集合的根節點 2. 將其中一個集合的根節點連到另外一個的根節點 ---- 以下圖為例 <div style="position: absolute; right: 10%; top:30%;">  </div> <div style="position: absolute; left: 0%; top:30%;">  </div> ---- 合併 $2$ 所在的的集合跟 $7$ 所在的集合 : 1. 先找到 $2$ 的根節點 =$1$，$7$ 的根節點 =$6$ 2. 將其中一個根節點的父節點設為另一個根節點 $7$ 所在的集合所有元素的根節點都會變成 $1$ ---- ### union 函數 這邊合併的函數名稱不使用 union 因為 union 為關鍵字 (撞名內建函數)，因此名稱改用 merge ```cpp= void merge(int x,int y) { // 合併 x, y 所在集合 x = find(x); // x 找到其根節點 y = find(y); // y 找到其根節點 if(x != y) // 如果 x,y 原本就屬於同一個集合則不需合併 f[y] = x; // 將其中一個根節點連到另一個 } ``` ---- ### 初始化 一開始每個元素皆屬於屬於不同集合 (自己就是一個集合) - 將節點指向自己，每個元素都是根節點 ```cpp= int f[N]; void init(){ for(int i=0;i<n;i++) f[i] = i; // 將每個元素根節點設為自己 // 或者也可以使用 iota(f, f+n, 0); 代替迴圈 } ``` ---- ### 完整程式碼 ```cpp= void init(){ for(int i=0;i<n;i++) f[i]=i; } int find(int x){ if ( x == f[x] ) // 如果當前節點為 f[x] == x return x; // 則為根節點 return find(f[x]); // 否則繼續往父節點方向找根節點 } void merge(int x,int y){ x = find(x), y = find(y); if(x != y) f[y] = x; } ``` ---- ### 優化 1 在最差的情況下， 合併後的樹有可能會變成一條鏈 $\Rightarrow$ find() 複雜度退化成 $O(n)$ 以右圖為例， find($5$) 需要跑完全部節點才能找到根 <div style="position: absolute; right: 10%; top:0%;">  </div> ---- 顯然是因為樹高太高，導致 find 最差複雜度太大 所以該如何降低樹高呢? ---- ### 啟發式合併 #### Union by Rank 記錄每棵樹的大小，在每次合併的時候， 將小的集合合併到大的集合 ---- ### 做法 宣告 $\text{sz}$ 陣列，紀錄每個節點的為根的集合大小 在初始化的時候將每個集合大小 $\text{sz}[i]$ 都設成 $1$ ```cpp= void init(){ for(int i = 0; i < n; i++){ f[i] = i; sz[i] = 1; } } ``` ---- 當遇到合併操作時，將兩個集合合併成一個時 把小的集合往大的集合合併 ---- 找到根節點，根節點儲存整個集合的資訊 合併時，把小的集合的資訊加給大的集合 ```cpp= int f[N], sz[N]; void merge(int x, int y) { x = find(x), y = find(y); if(x == y) return; if(sz[x] < sz[y]) swap(x, y); // 將 x 變成大的 sz[x] += sz[y]; // 把集合 y 的大小加到集合 x f[y] = x; } ``` ---- ### 分析 合併兩棵樹高不同的樹  ---- 兩個不同的集合合併，如果把樹高比較矮的連往比較高的， 合併後的樹高不會改變  ---- 而如果合併的兩個集合樹高相同， 或者高的往矮的合併，則合併後樹高會+1   ---- 每次把小的合併到大的方法，稱之為啟發式合併 使用此方法的合併的樹， 在最差情況下，每次合併時兩棵樹的樹高都相同 ---- 在樹高相同的情況下，會發現每次樹高要 $+1$ 所需節點數量會變 $2$ 倍  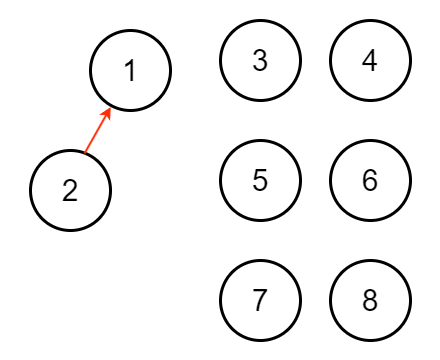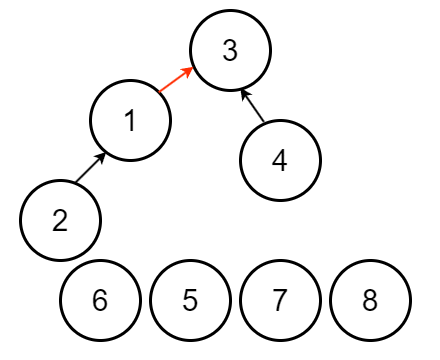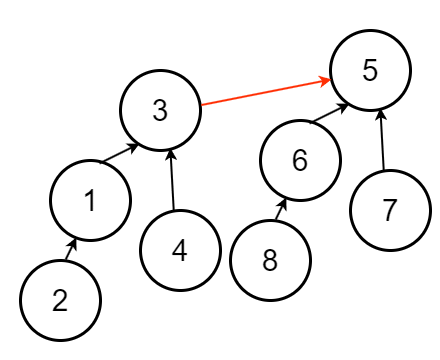因此 $n$ 個節點時，使用啟發式合併樹高最高為 $O(\log n)$ ---- ### 優化 2 #### 路徑壓縮 在每次 find 的時候，把經過節點的父節點全部設成根節點 ```cpp= int find(int x){ if(f[x] == x) return x; f[x] = find(f[x]); // 直接將 x 的父節點設成根節點 return f[x]; } ``` <!--可以再模擬一下 f[x] = find(f[x]) 的地方 --> ---- 呼叫 find($5$) 會經過節點 $5$ $4$ $3$ $2$ $1$ 將中間每個節點的父節點直接設為根節點 <div style="position: absolute; right: 70%; top:100%;">  </div> <div style="position: absolute; right: 60%; top:200%;"> $\rightarrow$ </div> <div style="position: absolute; right: 10%; top:150%;">  </div> 修改後，之後詢問這些節點時，只需要 $O(1)$ 就會找到根節點 ---- 使用啟發式合併+路徑壓縮 能使得單次操作複雜度降到 $O(\alpha(N))\approx O(1)$ ($\alpha( 2^{2^{10^{19729}}} ) \approx 5$) 因此併查集操作複雜度幾乎是常數時間 ---- ### 完整程式碼 要特別注意合併時，如果兩個元素本來就在同一個集合 要直接回傳，不要重複加到 sz (15行) ```cpp= int f[N], sz[N]; void init(){ for(int i=0;i<n;i++) { f[i] = i; sz[i] = 1; } } int find(int x){ if ( x == f[x] ) // 如果當前節點為 f[x]==x return x; // 則為根節點 f[x] = find(f[x]); return f[x]; } void merge(int x, int y) { x = find(x), y = find(y); if(x==y) return; if(sz[x] < sz[y]) swap(x, y); // 將 x 變成大的 sz[x] += sz[y]; f[y] = x; } ``` ---- ### 紀錄集合資訊 如果題目為給定 $n$ 個元素，每次操作為以下其中一種 : 1. 查詢元素 $x$ 所在的集合有幾個元素 2. 合併元素 $x, y$ 分別所在的集合 ---- ### 查詢集合大小 會發現集合大小在做啟發式合併時， 就已經記錄過此資訊 $\text{sz[ ]}$ 了 查詢元素 $x$ 所在的集合大小只需要找到 $x$ 的集合的根節點， ```cpp sz[find(x)] ``` 即為所在的集合的大小 ---- ### 其他資訊查詢 如果題目需要求其他資訊，如集合內編號最小/大值等等， 則多為一個陣列 $\text{mn[ ]}$/$\text{mx[ ]}$ 之類維護每個集合內的資訊 合併集合時，則把兩個集合內的資訊合併 ```cpp= void merge(int x){ x = find(x); y = find(y); if(x == y) return; if(sz[x] < sz[y]) swap(x, y); mn[x] = min(mn[x], mn[y]); mx[x] = max(mx[x], mx[y]); f[y] = x; } ``` ---- ### 相異集合的數量 要找總共有幾個集合，可以找總共有幾個根節點即可 ```cpp= int countComponent(){ int ret = 0; for(int i = 0; i < n; i++){ if(find(i) == i) ret++; } return ret; } ``` --- ## 經典 DSU 例題 ---- ### 連通塊 / 連通分量 / 連通元件 #### (connected component) 一個無向圖中的極大連通子圖  ---- ### 找最大連通塊 給一張 $n$ 個節點的圖，一開始有 $m$ 條邊， 接下來有 $k$ 次操作，每次操作為新增一條邊， 每次操作完輸出最大的連通塊大小 ? - $n, m, k\le 10^5$ ---- 下圖為例，黑色為一開始的邊，紅色為依序要加入的邊  當加完 $1$ 號邊之後，最大連通塊大小為 $5$ 當加完 $2$ 號邊之後，最大連通塊大小為 $5$ 當加完 $3$ 號邊之後，最大連通塊大小為 $6$ ---- 不難發現，原圖可以看成三個獨立的節點集合 加入邊的行為相當於對集合做兩兩合併  ---- ### [Almost-union-find](https://zerojudge.tw/ShowProblem?problemid=f292) 一個有三種操作的並查集 : 1. $\text{Union}(x, y)$: 把元素 $x, y$ 分別所在集合合併成同一集合 2. $\text{Move}(x, y)$: 將元素 $x$ 移動到元素 $y$ 所在的集合 3. $\text{Return}(x)$: 詢問元素 $x$ 所在的集合內元素個數與元素編號總和 $1\le n, m\le 10^5$ ---- 可以發現操作 1、3 都是正常的並查集操作 只需要在 merge 的時候維護總和(sum)跟大小(sz) ```cpp void merge(int x, int y){ x = find(x); y = find(y); if(x == y) return; if(sz[x] < sz[y]) swap(x, y); sz[x] += sz[y]; num[x] += num[y]; f[y] = x; } ``` 而操作 2 比較不一樣，需要做到刪除的操作。 ---- 我們可以從兩種情況來看刪除 1. 移除的是葉節點 2. 移除的不是葉節點 ---- ### 1. 移除的是葉節點 在這個情況下， 只要將根節點記錄大小跟總和的變數把這個節點減掉即可 ---- ### 2. 移除的不是葉節點 感覺很麻煩，我也不會 ---- ### 捨棄原本的節點 每次詢問，需要回傳集合內元素個數與元素編號總和 把元素 $x$ 移除，其實只需把 $x$ 儲存在集合內的資訊移除即可 ```cpp= void remove(int x){ root = find(x); sz[root]--; sum[root] -= x; } ``` 移除後，原本的節點就不重要了。 ---- ### 加入到新的集合中 要將 $x$ 加入新集合， 可以先給 $x$ 一個新的編號 $\text{newid}$ 來代表數字 $x$ 因此需要開一個陣列 $\text{id[ ]}$ 維護每個元素當前代表的編號， 並初始化新編號的 $\text{sz[ ], num[ ]}$ ---- ### 換新編號 & 合併 x 與 y 的集合 ```cpp void add(int x){ f[id[x]] = id[x] = newid++; sz[id[x]] = 1; sum[id[x]] = x; } remove(x); add(x); merge(id[x], id[y]); ``` --- ## 找最小生成樹 #### Kruskal 演算法 ---- ### 最小生成樹定義 (Minimum Spanning Tree) 給一張帶權圖， 最小生成樹是其中所有的生成樹中，權重總和最小的 簡稱 MST ---- ### 複習: 邊陣列 ```cpp= struct Edge{ int u, v, w; // 點 u 連到點 v 並且邊權為 w }; Edge g[200005]; // 宣告 Edge 型態的陣列 g ``` ---- struct 可以自定義運算子 多載 "$<$" 運算子，使用邊權重比較兩條邊的大小關係 ```cpp= struct Edge{ int u, v, w; // 點 u 連到點 v 並且邊權為 w bool operator<(const Edge& rhs){ return w < rhs.w; //兩條邊比較大小用邊權比較 } }; Edge g[200005]; // 宣告 Edge 型態的陣列 graph ``` ---- ### 找最小生成樹 1. 將所有邊照權重大小排序 2. 從權重小的邊開始窮舉，依序窮舉到大 - 當邊兩側的節點原本不連通就加邊 - 否則就捨棄這條邊 3. 當大小為 $n$ 時，停止窮舉 Kruskal 演算法其實是一種 greedy algorithm <!-- .element: class="fragment" data-fragment-index="1" --> ---- ### 加入邊 使用併查集，一開始所有點都沒連任何邊 因此所有點都屬於自己的集合 當兩個點有連邊，代表他們屬於同一個集合 因此可以用並查集判斷，判斷是否已經為同一個集合 ---- <div style="background-color:white; position: absolute; right: 20%;">  </div> ---- ### 程式碼 將邊照大小依序嘗試加入圖中， 如果邊的兩點未連通，則連通兩點 ```cpp= sort(graph, graph + m); // 將邊照大小排序 int ans = 0; for(int i = 0; i < m; i++){ //>:) if(find(graph[i].u) != find(graph[i].v)){ // 如果兩點未聯通 merge(graph[i].u, graph[i].v); // 將兩點設成同一個集合 ans += graph[i].w; // 權重加進答案 // 終止條件 : 當並查集大小等價於樹內點的數量 if(sz[find(graph[i].u)] == n) break; } } cout << ans << endl; ``` ---- ### 複雜度分析 依照權重排序所有邊 $O(M\log M)$ 窮舉每條邊加入 $O(M\cdot \alpha (N))$ $\Rightarrow$ 總複雜度 $O(M\log M)$ ---- ### 演算法的正確性 憑什麼 Kruskal 演算法跑出來的 $T$ 就是 MST 呢? ---- 在加入邊 $e$ 時，若未形成環，則當然是當前最佳選擇 在加入邊 $e$ 時，若形成一個環 - 先違反一下 Kruskal 的方法， 挑 $e$ 後拔掉環上其他邊也會是一棵生成樹 - 由於演算法會先對權重排序，環上其他邊的權重 $\le w(e)$ $\Rightarrow$ 挑 $e$ 後拔掉環上其他邊不會比較好 - 因此反證回來 Kruskal 的挑法的確比較好 最後得到一棵生成樹，自然就是 MST ---- ### 瓶頸生成樹 令 $\tau = \{T_i\}_{i\in I}$ 是這張圖的所有生成樹， 瓶頸生成樹 $T^*$ 的最大邊權值為所有 $T_i$ 的最小 --- ## 作業 & 練習時間 ---- Any question?