<style> .reveal .slides { text-align: left; font-size:35px } </style> ## 圖論 & 圖上遍歷 11/3 preTrain --- ## Table of Contents - 圖論簡介 - 圖論名詞定義 - 走訪圖的一些名詞 - 一些圖的變體 ---- - 建圖方法 - 鄰接矩陣 - 鄰接串列 - 邊陣列 - 圖上遍歷 - DFS - BFS - 經典例題與應用 --- ## 圖論簡介 ---- 以前人們對空間中的認識是用數字來描述 (像是角度、長度等) 然而在 $18$ 世紀時有一個問題卻無法用古典的幾何學來解 ---- ## [七橋問題](https://zh.wikipedia.org/zh-tw/%E6%9F%AF%E5%B0%BC%E6%96%AF%E5%A0%A1%E4%B8%83%E6%A1%A5%E9%97%AE%E9%A2%98) 在所有橋只能走過一遍的情況下，如何才能將所有橋走遍?  ---- <div style="position: absolute; left: 0%; top:90%;"> [大數學家歐拉](https://en.wikipedia.org/wiki/Leonhard_Euler) 給出的解答: 此走法並不存在!! 透過一座橋進入一塊陸地， 就一定要有另一座橋可以走出來 $\Rightarrow$ 每塊陸地除了起點與終點之外， $\quad$ 都要有**偶數**座橋連接 此結論並沒有用到任何幾何解釋 完全是一個新的領域 這就是圖論的起源 <!-- .element: class="fragment" data-fragment-index="1" --> </div> <div style="position: absolute; right: 0%; top:100%;">  </div> ---- ### 圖論之後的發展 - 此後幾十年，圖論一直沒被受到重視 - 十九世紀中末，開始有人提出圖論相關問題，也開始使用「圖」一詞 - Kőnig 在 $1936$ 第一本圖論教科書，奠定圖論作為一門學科的基礎 - [四色定理](https://en.wikipedia.org/wiki/Four_color_theorem): 用電腦窮舉出來，但數學家不想承認的定理 - 近代在組合學/計算機領域有非常多應用 --- ## 圖論名詞定義 ---- ### 圖 Graph 一張圖裡面我們只關心「節點」與「節點之間的連接關係」 數學上的圖由一個 triple 組成 - $V$ 為節點集合 - $E$ 為邊集合 - 邊與點對的 relation 表示為 $G=(V, E)$ ---- ### 一些名詞 以單一節**點 (vertex)** $v\in V$ 看來，回有很多條邊連接 - 一個節點連接的邊數稱作**度數 (degree)** : $\deg(G)$ - 兩節點 $u, v$ 之間僅隔一條邊 : 稱 $u, v$ **相鄰 (adjacent)** - 點的個數寫作 $|V|$ 或 $n$ ---- ### 一些名詞 **邊 (edge)** $e\in E$ 必有兩個**端點 (endpoints)** $(u, v)$，其中: - 一條邊 $e$ 與節點 $v$ 相接 : $v, e$ **關聯(incidence)** - 若 $u=v$，則稱 $e$ 為**自環 (self loop)** - 若存在 $e'=(u, v)$，則 $e'=e$ 稱 $u, v$ 存在**多重邊 (multiple edges)** - 邊的個數寫作 $|E|$ 或 $m$ ---- ### 舉個例子  - $3$ 與 $5$ 相鄰、$2$ 與 $f$ 關聯 - $|V|=6$、$|E|=8$ - 此圖不存在自環或多重邊 ---- 通常來說，我們希望討論的圖不存在自環與重邊 - 我們稱這種圖為**簡單圖 (simple graph)** ---- ### 有向圖 複習一下圖 $G=(V, E)$ 的定義: - $V$ 為節點集合 - $E$ 為邊集合 - 邊與點對的 **relation** 根據第三點的定義，$e=(u, v)=(v, u)$ 成立 $\Rightarrow$ 我們稱這種圖為**無向圖 (undirected graph)** ---- ### 有向圖 若把 $G=(V, E)$ 定義改成 : - $V$ 為節點集合 - $E$ 為邊集合 - 邊與點對的 **function** 根據第三點的定義，$e=(u, v)\neq (v, u)$ $\Rightarrow$ 我們稱這種圖為**有向圖 (directed graph)** ---- ### 圖論第一定理 / 度數和定理 給一張無向簡單圖 $G=(V, E)$，則 $$ \sum_{v\in V}deg(v)=2|E| $$ ---- ### 圖的計數 給一張簡單圖，由定義不難推出: - 無向圖最多 $C^n_2=\cfrac{n(n-1)}{2}$ 條邊 - 有向圖最多 $2\times C^n_2=n(n-1)$ 條邊 ---- ### 一些圖的定義 - 若圖的邊數達到最多，則稱為**完全圖 (complete graph)** - 若 $|V|=0$ 且 $|E|=0$，則稱為**空圖 (null graph)** ---- ### 子圖 (subgraph) 邊集合點集合皆為原圖的子集合，則稱此圖為原圖的子圖  ---- ### 圖的補圖 (completement) 若兩張圖 $G, G'$ 點集相同，邊集互斥，則兩張圖互為補圖  ---- ### 同構 (isomorphic) 有時我們會發現兩圖看起來不相同，但他們節點之間的連接關係卻一模一樣，則我們會稱兩圖同構  我們通常可以透過**重新編號**來獲得同構的圖 --- ## 走訪圖的一些名詞 以下假設圖都是無向簡單圖 <!-- .element: class="fragment" data-fragment-index="1" --> 有向圖的版本也都雷同，就給各為自己去想想 <!-- .element: class="fragment" data-fragment-index="2" --> ---- ### 道路 (walk) 若我們在一張圖上隨便走，會產生序列 : $\langle v_0, e_1, v_1,e_2, v_2\cdots, v_{k-1}, e_k,v_k\rangle$ 稱這是一條長度為 $k$ 的 walk 總共 $k+1$ 個節點與 $k$ 條邊 <!-- .element: class="fragment" data-fragment-index="1" --> ----  walk: $\langle a,1,b,3,c,4,d,6,e,5,c,4,d,6,e\rangle$ ---- ### 行跡 (trail) 若我們在 walk 上多加限制 : 不可走已走過的邊 則稱此為 trail  ---- ### 路徑 (path) 若我們在 trail 上再多加一個限制 : 不可走已走過的邊 則稱此為 path  ---- 若以上三種序列的頭尾相同則會在前面加一個**閉 (closed)** - 閉道路 (closed walk) - 閉行跡 (closed trail) - 閉路徑 (closed path) 與之相對的就是**開 (open)** ---- ### 迴路 (circuit) 閉行跡就是迴路 ---- ### 環 (cycle) 閉路徑就是環 ---- ### 小整理 ||邊 edge|點 vertex|開 open|閉 closed| |---|---|---|---|---| |道路 walk|可重複|可重複|開道路|閉道路| |行跡 trail|不重複|可重複|開行跡|閉行跡 (迴路)| |路徑 path|不重複|不重複|開路徑|閉路徑 (環)| ---- ### 小小的定理 每個 $u, v\text{-walk}$ 都包含一條 $u, v\text{-path}$ 這可以對長度做歸納法，證完你會更了解以上這些名詞的關係 <!-- .element: class="fragment" data-fragment-index="1" --> ---- ### 連通 (connected) - 無向圖 : 存在一條路徑兩端點為 $u, v$，則節點 $u$ 與 $v$ 連通 - 有向圖 : 有很多種連通關係 (橋連通、雙連通、強連通 $\cdots$) 下學期會教 ---- ### 簡單的小問題 假設有 $n$ 個節點，請問最少需要幾條邊才能使所有點連通呢? ans : $n-1$ 條 <!-- .element: class="fragment" data-fragment-index="1" --> ---- ### 樹 (tree) 連通且邊數為 $n-1$ 的圖  這個性質還蠻重要的，記起來!! <!-- .element: class="fragment" data-fragment-index="1" --> ---- ### 小小的定理 以下四種定義樹的方式等價: 1. 連通無環圖 2. 連通且邊數為 $n-1$ 的圖 3. 無環且邊數為 $n-1$ 的圖 4. 無自環且任兩點僅存在唯一路徑的圖 --- ## 一些圖的變體 ---- 有時候一般的圖可能很難描述我們遇到著狀況 所以通常會賦予一張圖一些額外的性質 ---- ### 帶權邊 這是在我們描述距離的時候可以用 之後講最短路的時候會用到  ---- ### 帶權點 我懶得畫，但題目有時會出現 ---- ### 點著色  這是維基百科上的 Petersen graph <!-- .element: class="fragment" data-fragment-index="1" --> ---- 競程通常只會遇到圖兩種顏色 三種或以上的通常是難題或可能是一些 理論上根本無法計算的東西 --- ## 建圖方法 ---- ### 鄰接矩陣 (Adjacency Matrix) - $n\times n$ 的矩陣，其中 $A_{ij}$ 代表點 $i$ 是否連通或是指向點 $j$ - 若為帶權圖則 $A_{ij}$ 存 $i$ 到 $j$ 的邊權 - 若圖有重邊也可以令 $A_{ij}$ 存邊 $(i,j)$ 的數量 - 空間複雜度 $O(n^2)$ - 遍歷圖的時間複雜度 $O(n^2)$ - 由於複雜度高因此不常在算法中使用 - 鄰接矩陣在數學上與圖是等價的 - 這種矩陣是存在一些運算規則的，但很複雜 ---- - 無向圖的矩陣會對稱 - 有向圖則不一定會對稱  ---- - 無權圖用 $0/1$ 表示兩點間是否有連邊 - 帶權圖則會寫數字，0 則代表中間沒連邊  ---- ### 鄰接串列 (Adjacency Lists) - $n$ 個串列，第 $i$ 個串列存 $i$ 所指向的邊(點) - 若為帶權圖，則串列可以存 pair(目標點,邊權) - 通常以 vector 實作，也就是 vector 陣列或二維 vector - 空間複雜度 $O(m)$ - 遍歷圖的時間複雜度 $O(m)$ - 最常使用的儲存方式 ----  ----  ---- ### 無權無向圖 在點 $u$ 和點 $v$ 之間連邊 本質上是存 $u\to v$ 與 $v\to u$ 的兩條邊 ```cpp= vector<int> edge[100005]; for(int i = 0, u, v; i < m; i++){ cin >> u >> v; edge[u].push_back(v); // u -> v edge[v].push_back(u); // v -> u } ``` ---- ### 帶權有向圖 新增一條點 $u$ 指向點 $v$ 權重為 $w$ 的邊 ```cpp= vector<pair<int, int>> edge[100005]; for(int i = 0, u, v, w; i < m; i++){ cin >> u >> v >> w; edge[u].push_back(make_pair(v, w)); } ``` ---- ### 初始化 就是清空而已 ```cpp= void init(){ for(int i = 0 ; i <= n; i++){ edge[i].clear(); } } ``` ---- ### 邊陣列 - 開一個 pair / struct 陣列把所有邊儲存起來 - 用於最小生成樹 (下周會講) - 不適合拿來遍歷 ---- #### 無權邊 ```cpp= pair<int, int> edges[100005]; for(int i = 0; i < m; i++){ cin >> edges[i].first >> edges[i].second; } ``` #### 帶權邊 ```cpp= struct Edge{ int u, v, w; }edge[100005]; for(int i = 0; i < m; i++){ cin >> edge[i].u >> edge[i].v >> edge[i].w; } ``` --- ## 圖上遍歷 ---- ### 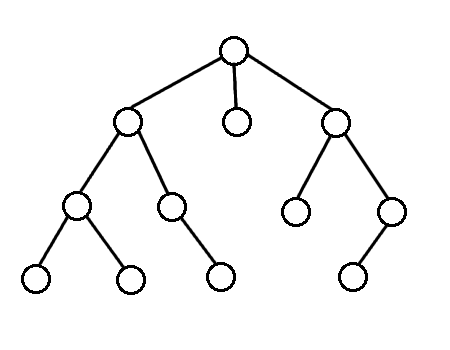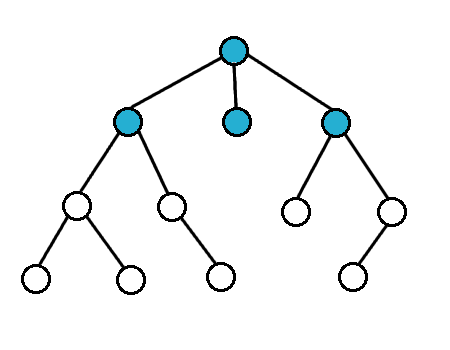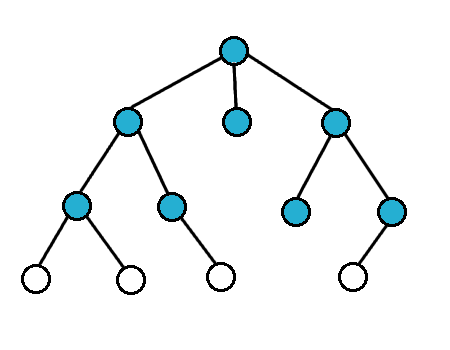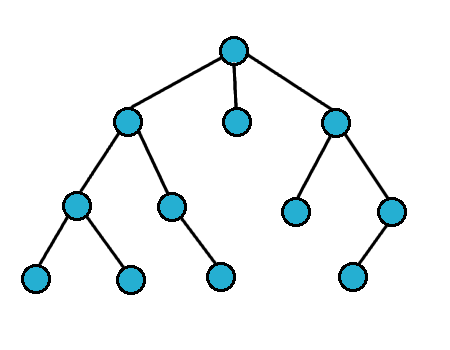廣度優先搜索(Breadth-First-Search,BFS) - 從起點開始往外散開 - 以迴圈 +queue 實作，寫起來較麻煩 - 對於無權圖，BFS 可找出到起點的最短路徑 - 時間複雜度 $O(E)$ (若用鄰接串列) - 由於較難寫因此較少用，常用在找不帶權最短路 ----  ---- ```cpp bool vis[MXN]; void bfs(int s){ queue<int> q; q.push(s); vis[s]=1; while(!q.empty()){ int x=q.front();q.pop(); for(int i:edge[x]){ if(!vis[i]) q.push(i),vis[i]=1; } } } ``` ---- ### 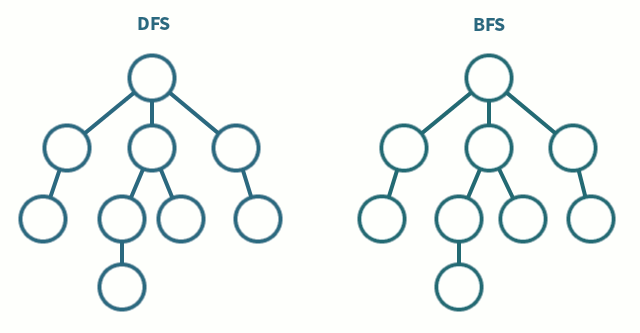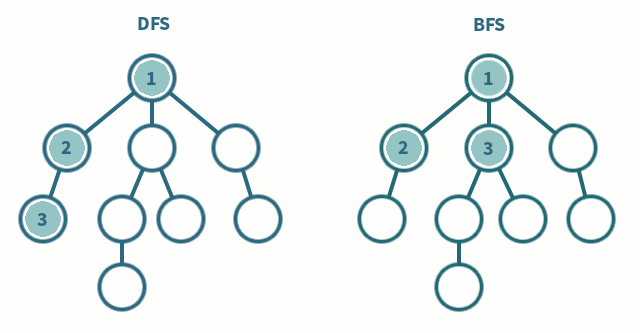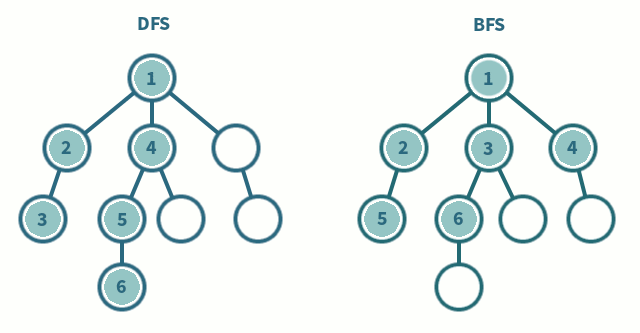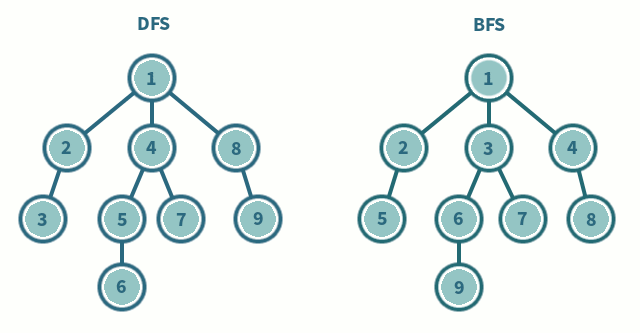深度優先搜索(Depth-First-Search, DFS) - 優先往深的地方走 - 通常以遞迴實作，直觀好寫(也可以使用stack取代遞迴) - 時間複雜度$O(E)$(若用鄰接串列) - 由於好寫，以及遞迴方便維護，有很多好的性質，因此是最常用的搜索方法 - 然而遞迴過深有可能導致stack overflow(RE)，遇到時只得改成用迴圈+stack實作(或一些毒瘤方法) ---- ### 實作範例 ```cpp void dfs(int x){ vis[x]=1; for(int i:edge[x]){ if(!vis[i]) dfs(i); } } ``` ----  --- ## 經典例題與應用 ---- ### 圖上最短路 由於 BFS 是一層一層的 從起點開始往外遍歷，同一層都遍歷過才往下一層遍歷 因此走到當前節點時會是從起點到自己最短的 ---- 多開一個 $\text{dis}$ 記錄從起點到自己距離 ```cpp= bool vis[MXN]; int dis[MXN]; void bfs(int s){ queue<int> q; q.push(s); vis[s] = 1; while(!q.empty()){ int x = q.front(); q.pop(); for(int i : edge[x]){ if(!vis[i]){ q.push(i), vis[i] = 1; dis[i] = dis[x] + 1; } } } } ``` 為什麼 $\text{dis}$ 會最短呢? <!-- .element: class="fragment" data-fragment-index="1" --> ---- $s$ 到 $v$ 的最短距離我們記做 $\delta(s, v)$ - 若 $s$ 到 $v$ 之間沒有路徑，則 $\delta(s, v)=\infty$ - 若存在一條邊 $(v, u)$，則存在三角不等式: $\delta(s, v)\leq \delta(s, u) + 1$ ---- <div style="position: absolute; left: 0%; top:90%;"> 舉個例子: 假設我們的圖長這樣 - 那 $\text{dis}[s]=0$ - 先訪問 $v$ 後 $\text{dis}[v]=1$ - 之後一定先走 $(s, u)$ 而不是 $(v, u)$ 所以 $\text{dis}[v]=dis[s]+1=1$ </div> <div style="position: absolute; right: 0%; top:90%;">  </div> ---- 換句話說就是 走訪的順序保證了每次紀錄 $\text{dis}$ 都是 $$ \text{dis[前面的節點]} < \text{dis[後面的節點]} $$ ---- ### 二分圖判斷 判斷題目給你的圖是不是一個二分圖 - 二分圖：一個無向圖中的點可以被分成兩個集合，使得同集合內的點互不相鄰 - 換句話說：黑白染色將圖上的點塗成黑或白，使得每條邊的兩端必不同色 ---- ### 想想看 這是二分圖嗎? <div style="position: absolute; left: 0%; top:90%;">  </div> <div style="position: absolute; right: 0%; top:90%;"> ans : 是  </div> <!-- .element: class="fragment" data-fragment-index="1" --> ----  - 左邊是一個二分圖，因為它可以被分成左右兩側的集合，兩側左側塗黑，右側塗白 - 右側不是一個二分圖，因為不管怎麼塗兩種顏色，一定有一條以上的邊兩端顏色都一樣 ---- ### 如何判斷二分圖 - 在 BFS/DFS 會遍歷所有點，會發現在拜訪路徑上的點一定是黑白交錯 - 選擇一個點開始塗黑 or 白，接著一直往下走，塗成另外一個顏色，一直這樣走下去 - 接下來判斷所有的邊，是否兩端都是不同顏色 ---- ### 實作範例 ```cpp= int color[N]; // -1: 沒塗色, 0: 黑色, 1: 白色 void dfs(int u, int c) { color[u] = c; // 塗上顏色 for (int &v : g[u]) { if (color[v] != -1) // color[] 初始化為 -1 continue; // 所以 color[v] != -1 就是已拜訪過 v dfs(v, c ^ 1); // c ^ 1 可以用來切換 0/1 } } bool is_colorable(){ // <- 執行這個 dfs(1, 0); // 用 DFS 塗顏色 for (int u = 1; u <= n; u++) { // 判斷每條邊兩端點的顏色 for(int &v : g[u]) { if(color[u] == color[v]) return false; } } return true; } ``` ---- 當然這兩件事也可以寫在一起 因為 BFS/DFS 實際上也會找到所有的邊 ```cpp= bool is_bigraph = 1; int color[N]; // 0: 沒塗色, 1: 黑色, 2: 白色 void dfs(int x, int x_color){ color[x] = x_color; for(int i : edge[x]){ if(color[x] == color[i]){ // 遇到一樣的顏色，不是二分圖 is_bigraph = 0; } } for(int i:edge[x]){ if(color[i]==0){//沒塗過色 dfs(i,(x_color==1?2:1)); } } } dfs(1,1);//把1塗成黑色 ``` ---- ### 小小的定理 一張圖 $G$ 是二分圖 若且唯若 $G$ 不存在奇數環 \[Kőnig 1936\] 這就是判斷二分圖的另解，可以自己寫寫看 <!-- .element: class="fragment" data-fragment-index="1" --> 當然還有[其他方式](https://hackmd.io/@ShanC/Bipartite-Graph-Recog#Eigenvalue-正負成對出現) <!-- .element: class="fragment" data-fragment-index="2" --> ---- ### [水窪問題](https://zerojudge.tw/ShowProblem?problemid=f493) 給定 $n\times m$ 大小的矩陣，0 代表沒有水，1 代表有水， 問有多少個水窪。 ex : ```cpp 3 4 0 0 0 0 1 0 1 1 1 0 1 0 ans : 2 ``` ---- ### 解法 遍歷整個矩陣，每次遇到水就把那攤水使用 BFS/DFS 跑過一次全部消除，消除完就可以獲得數量。 ---- ### 網格圖遍歷 ```cpp= bool vis[1005][1005]; // 紀錄每個位置是否有走過 int arr[1005][1005]; // 紀錄水窪 void dfs(int x, int y){ if(vis[x][y] || arr[x][y] == 0) return; vis[x][y] = 1; arr[x][y] = 0; if(x+1 < n) dfs(x+1, y); if(x-1 >= 0) dfs(x-1, y); if(y+1 < m) dfs(x, y+1); if(y-1 >= 0) dfs(x, y-1); } ``` ---- 改用迴圈遍歷周圍格子點 ```cpp= bool vis[1005][1005]; // 紀錄每個位置是否有走過 int arr[1005][1005]; // 紀錄水窪 int dx[4] = {1,-1,0,0}; int dy[4] = {0,0,1,-1}; bool safe(int x, int y){ return x >= 0 && x < n && y >= 0 && y < m; } void dfs(int x, int y){ if(vis[x][y] || arr[x][y] == 0) return; vis[x][y] = 1; arr[x][y] = 0; for(int i = 0; i < 4; i++){ if(safe(x+dx[i], y+dy[i])){ dfs(x+dx[i], y+dy[i]); } } } ``` ---- ### [走迷宮問題](https://zerojudge.tw/ShowProblem?problemid=a982) 給定一個 $n\times n$ 的二維整數陣列，用來表示一個迷宮，數組中只包含 $0$ 或 $1$，其中 $0$ 表示可以走的路，$1$ 表示不可通過的牆壁。 最初，有一個人位於左上角 $(1,1)$ 處，已知該人每次可以向上、下、左、右任意一個方向移動一個位置。 請問，該人從左上角移動至右下角 $(n,n)$ 處，至少需要移動多少次。 ---- ### 解法 由於每次轉移都是從上下左右移動過來的， 所以只需要從起點開始將可到達的地方全部塞進去， 另外開一個陣列紀錄起點到他的最短距離。 ---- ### [倒水問題](https://vjudge.net/problem/UVA-10603) 給容量分別為 $a,b,c$ 的三杯水，倒法是一杯水到另一杯水倒到自己空或是別人滿為止，一開始 $a,b$是空的 $c$ 是滿的問是否能得到d的水如果不能則輸出 $d'$ (小於 $d$ 最大的容量) sample : ```cpp input 2 1 3 6 4 1 12 15 7 output 3 4 14 7 ``` ---- ### 解法 考慮每一個狀態當成一個節點， 把倒水後的狀態當成連向的節點建邊會形成一張有向圖  ----  (2,3,1) 把 c 的水倒到 a 中 (2,3,1) $\to$ (3,3,0) ---- ### 儲存節點狀態 可以宣告一個結構把每種容量的狀態紀錄起來 並用 map 紀錄每種狀態是否已經走過 ```cpp struct item{ int a, b, c; }; map<item, int> dis; int bfs(item start, item target){ queue<item> que; que.push(start); while(!que.empty()){ item it = que.front(); que.pop(); if(it == target){ return dis[it]; } // 窮舉每種倒水的情況 if(!dis.count(item(it.a + it.c, it.b, 0))){ //c->a dis[item(it.a + it.c, it.b, 0)] = dis[it]+1; que.push(item(it.a + it.c, it.b, 0)); } //c->b, a->b, a->c, b->c, b->a } } ``` ---- ## 畫圖工具 - [graph editor](https://csacademy.com/app/graph_editor/) - [graph online](https://graphonline.ru/en/) --- ## 作業 & 練習時間 ---- Any Question?