<style> .reveal .slides { text-align: left; font-size:35px } </style> # Graph Theory & DSU ---- - Graph Introducion - Disjoint Set(Union-Find) - Minimum Spanning Tree (kruskal) --- ## 名詞介紹 (以下內容也都會在資工其他領域學習到 ---- - 圖(graph)：由一些點與一些邊所組成，通常以 $G=(V,E)$ 表示 - 點(vertex)：節點，通常以 $V$ 表示 - 邊(edge)：連接兩點，通常以 $E$ 表示，$e=(u,v)$ 代表邊 $e$ 連接 $u,v$ 兩點，也就是 $u,v$ 為 $e$ 的端點 ---- ## 相關用語定義 - 權重(weight)：指圖的點/邊附帶的數值 - 點數/邊數：點/邊的數量，通常記為 $V/E(n/m)$ - 有向邊：邊可以分為無向邊(雙向)與有向邊(單向) - 重邊(multiple edge)：指兩點之間有多條邊連接 - 自環(self loop)：指兩端為同一點的邊 $e=(u,u)$ - 度數(degree)：一個點所連接的邊的數量，若是有向邊則又分為出度與入度 - 相鄰(adjacent)：指兩個點間有無向邊相連 - 指向(consecutive)：有向邊的起點"指向"終點 ---- ## 更多的定義 - 路徑(path)：從起始點到目標點上所經過的所有點，路徑上的點/邊皆可重複 - 簡單路徑(track)：點不重複的路徑 - 行跡(trace)：邊不重複的路徑 - 迴路(circuit)：邊不重複且起終點相同的路徑 - 環(cycle)：點不重複且起終點相同的路徑 - 連通(connected)：$u,v$ 連通若且唯若存在 $u$ 到 $v$ 或 $v$ 到 $u$ 的路徑，一群點連通代表這群點兩兩連通 ---- ## 各種圖的定義 - 簡單圖(simple graph)：沒有重邊與自環的圖 - 無向圖(undirected graph)：由無向邊組成的圖 - 有向圖(directed graph)：由有向邊組成的圖 - 連通圖(connected graph)：任兩點皆連通的圖 - 樹(tree)：無向無環連通圖(其實也可以有向) - 森林(forest)：只由樹組成的圖。按照定義，一棵樹也是森林 - 完全圖(complete graph)：任兩點都相鄰的圖 ---- ## 圖之間關係的定義 - 子圖(subgraph)：邊/點皆為原圖的子集 - 補圖(complement graph)：若兩張圖點集相同，邊集互斥且聯集為完全圖，則兩張圖互為補圖 - 同構(isomorphic)：不考慮編號長的完全相同的圖 - 生成樹(spanning tree)：點集相同且為樹的子圖 ---- ## 對於有根樹的定義 - 父節點(parent node)：對於除了根以外的每個節點，定義為從該節點到根路徑上的第二個節點。 根節點沒有父節點 - 祖先(ancestor)：一個節點到根節點的路徑上，除了它本身外的節點。 根節點的祖先集合為空 - 後代(descendant)：子節點和子節點的後代 - 子節點(child node)：如果 $u$ 是 $v$ 的父親，那麽 $v$ 是 $u$ 的子節點 - 深度(depth)：到根節點的路徑上的邊數 - 高度(height)：所有節點的深度的最大值 - 子樹(subtree)：刪掉與父親相連的邊後，該節點所在的子圖 --- ## Disjoint Set (Union-Find) (DSU) 並查集，又稱不相交集資料結構 ---- 並查集是一種樹狀結構 <!-- 大概說一下樹是什麼 --> 處理集合問題，主要有以下兩個操作 * 查詢元素所在集合(find) * 合併兩個集合(union) ---- 並查集只需要用一個長度為 $n$ 的陣列即可， 陣列內第 $i$ 格存的值為第 $i$ 個節點的父節點編號 ```cpp= int f[n]; f[3] // 節點 3 的父節點編號 f[5] // 節點 5 的父節點編號 ``` ---- ### 根節點 如果一個點為根節點，他的父節點為自己 (f[x] == x) 以下圖為例， 1、6 為根節點  ---- ## 判斷集合 定義兩個相異元素如果屬於同一個集合，則兩個元素會在並查集的同一棵樹上 ---- 如何判斷在同一棵樹上? ---- ## find 函數 find 函數會找到某個節點 x 的根節點 如果兩個點的根節點相同，代表在同一棵樹上， 也就是屬於同一個集合 ``` find(x) == find(y); ``` 則 x 與 y 所屬同一個集合 ---- ## find 函數 ```cpp= int find(int x){ if ( x == f[x] ) // 如果當前節點為 f[x]==x return x; // 則為根節點 return find(f[x]); } ``` ---- ## union 函數 如果有兩個節點 a, b 所在的集合想要合併成一個集合 做法為找到兩集合的根節點 將其中一個集合的根節點連到另外一個的根節點 以下圖為例  ---- ## union 函數 合併 2 所在的的集合 跟 7 所在的集合 則先找到 2 的根節點 =1, 7 的根節點 =6 將其中一個根節點的父節點設為另一個根節點  則 7 所在的集合所有元素的根節點都會變成 1 ---- ## union 函數 這邊合併的函數名稱不使用 因為 union 為關鍵字 (撞名內建函數） 因此名稱改用 merge ```cpp= void merge(int x,int y) // 合併 x, y 所在集合 { x = find(x); // x 找到其根節點 y = find(y); // y 找到其根節點 if(x != y) // 如果 x,y 原本就屬於同一個集合則不需合併 f[y]=x; // 將其中一個根節點連到另一個 } ``` ---- ## 初始化 一開始每個元素皆屬於屬於不同集合 因此會將節點指向自己，因為這時候每個元素都是根節點 ```cpp= int f[N]; void init(){ for(int i=0;i<n;i++) f[i] = i; // 將每個元素根節點設為自己 //或者也可以使用 iota(f, f+n, 0); 代替迴圈 } ``` <!-- --> ---- ## 完整程式碼 ```cpp= void init(){ for(int i=0;i<n;i++) f[i]=i; } int find(int x){ if ( x == f[x] ) // 如果當前節點為 f[x]==x return x; // 則為根節點 return find(f[x]); // 否則繼續往父節點方向找根節點 } void merge(int x,int y){ x=find(x), y=find(y); if(x!=y) f[y]=x; } ``` ---- ## 優化 在最差的情況下 合併後的集合的樹形有可能會變成一條鏈 $\rightarrow$ find() 複雜度退化成 $O(N)$  以上圖為例，find(5) 需要跑完全部節點才能找到根節點 ---- ## 啟發式合併 ### Union by Rank 記錄每棵樹的大小，並在每次合併的時候，將小的集合合併到大的集合。 ---- ### 做法 宣告 sz 陣列，紀錄每個節點的為根的集合大小 在初始化的時候將每個集合大小 sz[i] 都設成 1 ```cpp= void init(){ for(int i = 0; i < n; i++){ f[i] = i; sz[i] = 1; } } ``` ---- 當遇到合併操作時，將兩個集合合併成一個時 把小的集合往大的集合合併 ---- 找到根節點，根節點儲存整個集合的資訊 合併時，把小的集合的資訊加給大的集合 ```cpp= int f[N], sz[N]; void merge(int x, int y) { x = find(x), y = find(y); if(x==y) return; if(sz[x] < sz[y]) swap(x, y); // 將 x 變成大的 sz[x] += sz[y]; // 把集合 y 的大小加到集合 x f[y] = x; } ``` ---- ### 分析 如果是原本的做法 假設有 $n$ 個節點，合併 $n - 1$ 次 每次合併都由大小為 $i$ 的合併到大小為 $1$ 的，樹就會長成最差的情況（鏈） 每次查詢會退化到 $O(n)$  ---- ### 分析 合併兩棵樹高不同的樹  ---- 兩個不同的集合合併，如果把樹高比較矮的連往比較高的， 合併後的樹高不會改變  ---- 而如果合併的兩個集合樹高相同， 或者高的往矮的合併，則合併後樹高會+1   ---- 每次把小的合併到大的方法， 稱之為啟發式合併 使用此方法的合併的樹，在最差情況下 為每次合併時，兩棵樹的樹高都相同 ---- 在樹高相同的情況下，會發現每次樹高要 + 1 所需節點數量會變 2 倍  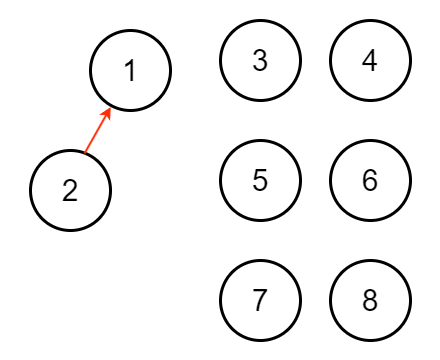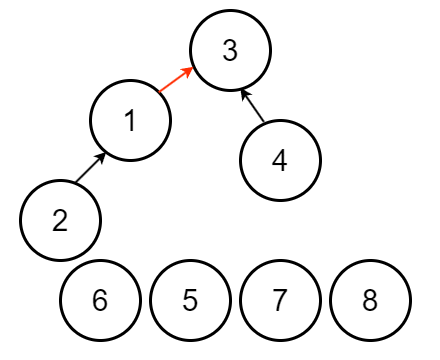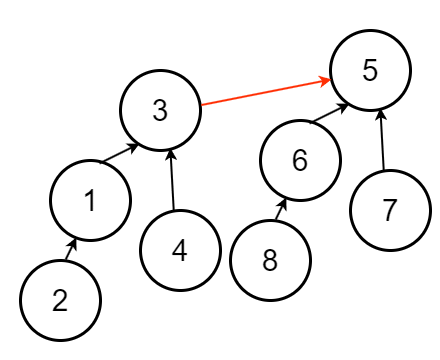因此 $n$ 個節點時，使用啟發式合併樹高最高為 $O(\log n)$ ---- ## 優化 2 ### 路徑壓縮 ---- ## 路徑壓縮 在每次 find() 的時候 把經過節點的父節點 全部設成根節點 ```cpp= int find(int x){ if(f[x] == x) return x; f[x] = find(f[x]); // 直接將 x 的父節點設成根節點 return f[x]; } ``` <!--可以再模擬一下 f[x] = find(f[x]) 的地方 --> ---- 呼叫 find(5) 會經過節點 5 4 3 2 1 將中間每個節點的父節點直接設為根節點 ```cpp= find(5) ``` <div style="position: absolute; right: 70%; top:100%;">  </div> <div style="position: absolute; right: 60%; top:200%;"> $\rightarrow$ </div> <div style="position: absolute; right: 10%; top:150%;">  </div> 修改後，之後詢問這些節點時，只需要 O(1) 就會找到根節點 ---- 使用啟發式合併+路徑壓縮 能使得單次操作複雜度降到 $O(\alpha(N))$ $O(\alpha(N))$ 趨近於 $O(1)$ ($\alpha( 2^{2^{10^{19729}}} ) = 5$) 因此並查集操作複雜度 幾乎是常數時間 ---- ## 完整程式碼 要特別注意合併時，如果兩個元素本來就在同一個集合 要直接回傳，不要重複加到 sz (15行) ```cpp= int f[N], sz[N]; void init(){ for(int i=0;i<n;i++) { f[i] = i; sz[i] = 1; } } int find(int x){ if ( x == f[x] ) // 如果當前節點為 f[x]==x return x; // 則為根節點 f[x] = find(f[x]); return f[x]; } void merge(int x, int y) { x = find(x), y = find(y); if(x==y) return; if(sz[x] < sz[y]) swap(x, y); // 將 x 變成大的 sz[x] += sz[y]; f[y] = x; } ``` <!-- --> ---- ## 紀錄集合資訊 如果題目為給定 $n$ 個元素，每次操作為以下其中一種 : 1. 查詢元素 $x$ 所在的集合有幾個元素 2. 合併元素 $x, y$ 分別所在的集合 ---- ## 查詢集合大小 會發現集合大小在做啟發式合併時， 就已經記錄過此資訊 sz[] 了 查詢元素 $x$ 所在的集合大小只需要找到 $x$ 的集合的根節點， ```cpp= sz[find(x)] ``` 即為所在的集合的大小 ---- 如果題目需要求其他資訊，如集合內編號最小/大值等等， 則多為一個陣列 mn[]/mx[] 之類維護每個集合內的資訊 合併集合時，則把兩個集合內的資訊合併 ```cpp= void merge(int x){ x = find(x); y = find(y); if(x == y) return; if(sz[x] < sz[y]) swap(x, y); mn[x] = min(mn[x], mn[y]); mx[x] = max(mx[x], mx[y]); f[y] = x; } ``` ---- ## 相異集合的數量 要找總共有幾個集合， 可以找總共有幾個根節點即可 ```cpp= int countComponent(){ int ret = 0; for(int i = 0; i < n; i++){ if(find(i) == i) ret++; } return ret; } ``` ---- ## 並查集在圖論上的意義 ---- 給一張 $n$ 個節點的圖，一開始有 $m$ 條邊， 接下來有 $k$ 次操作，每次操作為新增一條邊， 每次操作完輸出最大的連通塊大小 ? - $n, m, k\le 10^5$ ---- 下圖為例，黑色為一開始的邊， 紅色為依序要加入的邊  當加完 1 號邊之後，最大連通塊大小為 5 當加完 2 號邊之後，最大連通塊大小為 5 當加完 3 號邊之後，最大連通塊大小為 6 ---- ## 連通塊意義 在同一個連通塊中，在並查集中代表在同一個集合。 因此我們可以用並查集維護整張圖誰跟誰連通。 在圖上邊 (x, y) ，相對於 merge(x, y) 操作 ---- ## 並查集應用 ---- ### Almost-union-find 題序：一個有三種操作的並查集 1. Union(x, y): 把元素 x , y 分別所在集合合併成同一集合 2. Move(x, y): 將元素 x 移動到元素 y 所在的集合 3. Return(x):詢問元素 x 所在的集合內元素個數與元素編號總和 - $1\le n, m\le 10^5$ ---- 可以發現操作 1、3 都是正常的並查集操作 只需要在 merge 的時候維護總和(sum)跟大小(sz) ```cpp void merge(int x, int y){ x = find(x); y = find(y); if(x == y) return; if(sz[x] < sz[y]) swap(x, y); sz[x] += sz[y]; num[x] += num[y]; f[y] = x; } ``` 而操作 2 比較不一樣，需要做到刪除的操作。 ---- 我們可以從兩種情況來看刪除 1. 移除的是葉節點 2. 移除的不是葉節點 ---- ### 1. 移除的是葉節點 在這個情況下，我們只要將根節點記錄大小跟總和的變數把這個節點減掉即可。 ---- ### 2. 移除的不是葉節點 感覺很麻煩，我也不會 ---- ### 捨棄原本的節點 每次詢問，需要回傳集合內元素個數與元素編號總和 把元素 $x$ 移除，其實只需把 $x$ 儲存在集合內的資訊移除即可 ```cpp= void remove(int x){ root = find(x); sz[root]--; sum[root] -= x; } ``` 移除後，原本的節點就不重要了。 ---- ### 加入到新的集合中 要將 $x$ 加入新集合，可以先給 $x$ 一個新的編號 $newid$ 來代表數字 $x$ 因此我們需要開一個陣列 id[] 維護每個元素當前代表的編號， 並初始化新編號的 sz[], num[] ---- ### 換新編號 & 合併 x 與 y 的集合 ```cpp void add(int x){ f[id[x]] = id[x] = newid++; sz[id[x]] = 1; sum[id[x]] = x; } remove(x); add(x); merge(id[x], id[y]); ``` ---- ## 反著做回來的題目 ---- ## 例題 題序：給一張 $n$ 個點、$m$ 條邊的圖， <!-- 講圖是什麼--> 要做 $q$ 次操作，每次將一條邊拔掉 求每次拔掉後還有多少塊連通塊？<!-- 這邊要解釋什麼是連通塊--> 範圍： $n, m, q\le 10^6$ <!-- 不確定範圍要多少 --> ---- ### 做法 每次刪除後看有幾個連通塊需要花 $O(n + m)$ 的時間 而我們有 $q$ 次詢問，很明顯不能這樣做 那這題要怎麼用並查集維護連通塊呢？ ---- ### 做法 如果將刪除變成合併，就跟原本 3-34 的題目類似了? 因此我們可以將操作反過來做 從後往前做，可以發現這樣子操作就從刪除變成合併了！ --- ## 最小生成樹 :evergreen_tree: 「生成樹」。從一張圖取出一棵樹，包含圖上所有點。可能有許多種。 而最小生成樹是其中所有的生成樹中，權重總和最小的。 <div style="position: absolute; right: 60%; top:100%;">  </div> <div style="position: absolute; left: 57%; top:100%;">  </div> ---- ## Kruskal' algorithm greedy method , 將所有邊照權重大小排序，從權重小的邊開始窮舉，依序窮舉到大， 當邊兩側的節點原本不連通就加邊，否則就捨棄這條邊 這個做法是對的，但為什麼是對的 🤔 ---- ## 證明 生成樹的一個性質： :::info 對於兩個生成樹 $T_1$ 與 $T_2$ 和一條邊 $e \in T_1 \backslash T_2$ 存在 $e_2 \in T_2 \backslash T_1$ 使得 $(T_2\backslash \{e_2\})\cup \{e_1\}$ 依然是生成樹。 ::: 從 $T_1$ 拿出一條邊加入 $T_2$ 後，$T_2$ 會形成一個環，此時移除環上任一邊即可讓 $T_2$ 有 $n-1$ 條邊連通，這個時候 $T_2$ 也還會是一棵樹。 ---- Kruskal' algorithm 的證明： 令Kruskal演算法找到的生成樹為 $T$，而最小生成樹為 $T^*$ 如果有多個最佳解，令 $T^*$ 為與 $T$ 交集最大的一個。 如果 $T=T^*$ 就結束了，否則，令 $e_i$ 是只出現在 $T$ 的邊且編號最小 根據上面的性質，存在 $e_j \in T^* \backslash T$ 使得 $T^*$ 把 $e_j$ 換出去再把 $e_i$ 放進來仍是一棵生成樹。 ---- 假如 $i < j$，那 $e_i$ 的權重 $\leq e_j$ 的權重。但由於$T^*$是最小生成樹，這樣做出來的 $T$ 的權重會跟 $T^*$ 一樣(或更小)，但是與$T$的交集比 $T^*$ 大，矛盾。 假如 $i > j$，由於比 $j$ 前面的邊都在 $T$ 與 $T^*$ 中，根據 Kruskal 演算法的特性，在遇到 $e_j$ 時就會把 $e_j$ 加入 $T$ 中了，矛盾。 故得證 $T=T^*$ ---- <div style="background-color:white">  </div> ---- ## 加入邊 使用並查集，一開始所有點都沒連任何邊 因此所有點都屬於自己的集合 當兩個點有連邊，代表他們屬於同一個集合 因此可以用並查集判斷，判斷是否已經為同一個集合 ---- ## 結構 使用 struct 儲存邊 (邊的兩個端點 u, v、權重 w) 多載 < 小於運算子，使用邊權重比較兩條邊的大小關係 ```cpp= struct Edge{ int u, v, w; // 點 u 連到點 v 並且邊權為 w bool operator<(const Edge& rhs){ return w < rhs.w; //兩條邊比較大小用邊權比較 } }; Edge graph[200005]; // 宣告 Edge 型態的陣列 graph ``` ---- ## 程式碼 將邊照大小依序嘗試加入圖中， 如果邊的兩點未連通，則連通兩點 ```cpp= sort(graph,graph+m); // 將邊照大小排序 int ans=0; for(int i=0;i<m;i++){ //>:) if(find(graph[i].u) != find(graph[i].v)){ // 如果兩點未聯通 merge(graph[i].u,graph[i].v); // 將兩點設成同一個集合 ans += graph[i].w; // 權重加進答案 if(sz[find(graph[i].u)]==n) break; //當並查集大小等價於樹內點的數量 } } cout<<ans<<endl; ``` ---- ## 瓶頸生成樹 令 $T_i$ 是這張圖的所有生成樹，會有樹 $T^*$ 它的最大邊權值為所有 $T_i$ 的最小 性質: 最小生成樹是瓶頸生成樹的充分不必要條件。 即最小生成樹一定是瓶頸生成樹，而瓶頸生成樹不一定是最小生成樹。 ---- ## 複雜度分析 依照權重排序所有邊 $O(M\log M)$ 窮舉每條邊加入 $O(M\cdot \alpha (N))$ -> 總複雜度 $O(M\log M)$ --- ## Question Time and Practice https://vjudge.net/contest/661401