<style>
.reveal .slides {
text-align: left;
font-size:28px;
}
</style>
# Sqrt-Decomposition
----
- Sqrt-Decomposition on Math
- Sqrt-Decomposition the Case
- Sqrt-Decomposition on Sequence
- Mo's Algorithm
----
## 根號題的數值
| 複雜度 | 題目範圍 | 實際大小 |
| -------- | -------- | -------- |
| $\sqrt{n}$ | $10^9\sim 10^{14}$ | $3\cdot 10^4\sim 10^7$ |
| $n\sqrt{n}$ | $5\cdot 10^4\sim 3\cdot10^5$ | $10^7\sim 1.6\cdot 10^8$
---
## 數論分塊 --- [UVa11526 H(n)](https://onlinejudge.org/index.php?option=onlinejudge&Itemid=8&page=show_problem&problem=2521)
數論分塊可以在 $O(\sqrt{n})$ 的複雜度計算一些除法向下取整的總和的式子 $f(n)$
$f(n) = \sum_{i=1}^{n}\limits {\lfloor\frac{n}{i}\rfloor}$
以 $n = 13$ 為例
| <center>$i$</center> | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| ---- | - | - | - | - | - | - | - | - | - | - | - | - | - |
| $\lfloor\frac{n}{i}\rfloor$ | 13 | 6 | 4 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
----
## 範圍
$f(n) = \sum_{i=1}^{n}\limits {\lfloor\frac{n}{i}\rfloor}$
$1\le n \le 10^{12}$,顯然不能線性跑過去計算
----
## 先講結論
$\forall i = 1...n$,最多只有 $2\sqrt{n}$ 種不同的 ${\lfloor\frac{n}{i}\rfloor}$
----

可以發現當 $i\ge \sqrt{n}$ 時,$\lfloor\frac{n}{i}\rfloor$ 的值都 $\le \sqrt{n}$ ,也就是只有 $\sqrt{n}$ 種
再加上所有 $i<\sqrt{n}$ 的,可以發現 $\lfloor\frac{n}{i}\rfloor$ 只有 $\sqrt{n}$ 種
----
最多只有 $2\sqrt{n}$ 個不同的值,因此只需要枚舉每個數字$\times$出現的次數
總和即為答案,以 $n=13$ 為例
| <center>$i$</center> | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| ---- | - | - | - | - | - | - | - | - | - | - | - | - | - |
| $\lfloor\frac{n}{i}\rfloor$ | 13 | 6 | 4 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
$\sum_{i=1}^{n}\limits {\lfloor\frac{n}{i}\rfloor} = 13\times 1+6\times 1+4\times 1+3\times 1+2\times 2+1\times7$
----
## 枚舉數字與出現次數
可以發現對於相同的 $\lfloor\frac{n}{i}\rfloor$ 為連續的,因此只須找到每個 $\lfloor\frac{n}{i}\rfloor$ 的區間即可
而每個 $\lfloor\frac{n}{i}\rfloor$ 的右界位置在 $\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor$
以 $\lfloor\frac{13}{i}\rfloor = 2$ 為例,出現的區間在 $i=5\sim 6$
----
## 過程
因此我們只需從 $i = 1$ 開始,找到每個 $\lfloor\frac{n}{i}\rfloor$ 的右界計算總和,
再從下一個 $\lfloor\frac{n}{i}\rfloor$ 繼續加入答案中
```cpp=
for(long long i = 1, r; i <= n; i = r+1){
r = n / (n/i); // 右界
ans += (n/i) * (r-i+1); // (n/i) * 次數
}
```
而最多只有 $2 \sqrt{n}$ 個不同的 $\lfloor\frac{n}{i}\rfloor$,總複雜度 $O(\sqrt{n})$
---
## 根號題 --- 分 case 處理
類似於數論分塊,依照題目分成兩種 case 處理
$K = \sqrt{n}$,分成
- $i\le K$
- $i > K$
兩個不同的範圍有不同的性質,根據性質分別做不同的計算
在圖論的題目中,也有許多會用到此性質分 case 處理
----
## 經典題
有 $n$ 個正整數 $a_1, a_2, a_3...,a_n$,
且 $a_1+a_2+a_3+...+a_n=k$
問是否可以選一些數字 $a_i$ 總合為 $x$
$1\le n, k, x\le 2\cdot 10^5$
----
## 經典 DP 題 ?
<span>Subset sum !<!-- .element: class="fragment" data-fragment-index="1" --></span>
<span>但複雜度呢?<!-- .element: class="fragment" data-fragment-index="2" --></span>
<span>n 個數字總和最大為 k<!-- .element: class="fragment" data-fragment-index="3" --></span>
<span>O(nk)<!-- .element: class="fragment" data-fragment-index="4" --></span>
<span>:(<!-- .element: class="fragment" data-fragment-index="4" --></span>
----
## 實際上
把 $a_i$ 分成兩種 case:
- $a_i\le \sqrt{k}$,這種 case 的 $a_i$ 種類不超過 $\sqrt{k}$ 種
- $a_i > \sqrt{k}$,這種 case 的 $a_i$ 不超過 $\sqrt{k}$ 個
($a_1+a_2+a_3+...+a_n=k$)
----
## $a_i\le \sqrt{k}$
這種 case 的 $a_i$ 種類不超過 $\sqrt{k}$ 種
此種情況可以統計每個數字出現次數,去做有限背包問題
每種物品花 $O(k)$ 的時間做有限背包
$\to O(\sqrt{k}\times k\times \log{a_i})$
----
## $a_i> \sqrt{k}$
由於題目限制 $a_1+a_2+a_3+...+a_n=k$
這種 case 的 $a_i$ 不超過 $\sqrt{k}$ 個
不超過 $\sqrt{k}$ 個物品做背包問題
$\to O(\sqrt{k}\times k)$
----
如此一來兩種 case 的複雜度分別為
$$
\begin{cases}
O(k\sqrt{k}\times\log{a_i}) & a_i\le \sqrt{k}\\
O(k\sqrt{k}) & a_i> \sqrt{k}
\end{cases}
$$
而在 $a_i\le \sqrt{k}$ 的 case 複雜度比較高,因此可以把 k 設小一點
平衡一下複雜度
----
除此之外,$a_1+a_2+a_3+...+a_n=k$
這種序列最多只會有 $\sqrt{k}$ 種不同的 $a_i$ $(1+2+3+...+\sqrt{k} = k$)
此性質也可以用在一些特殊的題目上
----
## 例題2 --- Count triangles in a graph
給一張 $n$ 個點 $m$ 條邊的簡單無向圖,
求圖上有幾個三角形 (大小為 3 的環)
$1\le n, m\le 10^5$
經典圖上分 case 題,下圖答案為 3

----
以大部分圖上根號分 case 題來說,都會以 degree 來分 case
<span>對於degree<!-- .element: class="fragment" data-fragment-index="1" --></span> <span>$\ge\sqrt{m}$<!-- .element: class="fragment" data-fragment-index="1" --></span><span>的點,我們稱之為重點<!-- .element: class="fragment" data-fragment-index="1" --></span>
<span>$\le \sqrt{m}$<!-- .element: class="fragment" data-fragment-index="1" --></span> <span>的點稱之為輕點<!-- .element: class="fragment" data-fragment-index="1" --></span>
----
不過對於以下這一張圖,會發現每一個點的 degree 都為3
因此分成重點輕點根本就毫無意義
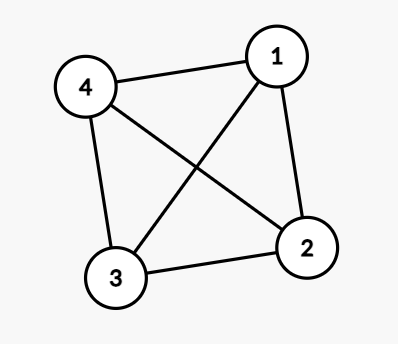
因此考慮把無向圖轉成有向圖,用每個點的 out_degree 去分 case
----
## 轉有向圖
讓原圖中 deg 大的點連向 deg 小的點,deg一樣就讓編號大的連向編號小的
重點和輕點就出現ㄌ

<center>圖中 n = 6 , m = 8</center>
----
## 觀察分完 case 的性質
- 對於所有的重點,可知重點的數量為 $\sqrt n$,連出去的點數量最多為 $n$
- 對於所有的輕點,輕點的數量為 $n$ ,連出去的點數量最多為$\sqrt n$
以這題來說,可以枚舉所有的點 $x$,用不同的 case 去計算有幾個三角形包含點 $x$
----
## 重點
假設這時存在一個重點 $x$ ,要算出對於 $x$ 來說,幾個三角形包含 $x$
可以觀察到點 $x$ 連出去的點集合 $s$,滿足
<center>
$deg[s_1] \le deg[s_2] \le ... \le deg[s_{deg[v]}] \le deg[v]$
$deg[s_1]+deg[s_2]+....+deg[s_{deg[v]}] \le m$
</center>
因此可以考慮
- 把點 $x$ 連出去的點集合 $s$ 中的點都打上標記
- 看打上標記的那些點連出去的那些點有沒有也被打上標記
- 把點 $x$ 連出去的點集合 $s$ 中的點都取消標記
----
## 重點
對於 5 來說,對他連出去的點都打上標記

----
看打上標記的那些點連出去的那些點有沒有也被打上標記,有的話就對答案造成貢獻

- 6 有連到 1、2 , 1、2都有被打上標記,答案 += 2
- 1 有連到 3 , 3有被打上標記,答案 += 1
- 2 誰都沒有連到,答案 += 0
- 3 有連到 4 , 4 沒有被打上標記,答案 += 0
算完之後取消標記即可
----
## 重點複雜度
總共有 $\sqrt m$ 個重點
對於每個連出去的點都打上標記 $O(m)$
看打上標記的那些點連出去的那些點有沒有也被打上標記 $O(m)$
取消標記 $O(m)$
總複雜度:$O(m \sqrt n)$
----
## 重點程式碼
```cpp
for (int x : heavy) { // 枚舉重點
for (int y : G[x]){
vis[y] = 1; //標記
}
for (int y : G[x]) {
for (int z : D[y]) {//直接暴力找
ans += vis[z];
}
}
for (int y : G[x]){
vis[y] = 0; //取消標記
}
}
```
----
## 輕點
輕點的做法跟重點一樣,也是做以下步驟
- 把點 $x$ 連出去的點集合 $s$ 中的點都打上標記
- 看打上標記的那些點連出去的那些點有沒有也被打上標記
- 把點 $x$ 連出去的點集合 $s$ 中的點都取消標記
但這樣複雜度會是好的嗎,我們來算看看複雜度
----
## 輕點
輕點最多有 $n$ 個,每個輕點的 deg 皆 $\le \sqrt m$
並且這些輕點的 deg 總和 $\le m$
----
## 輕點
對於所有輕點$x$,可知所有連出去的點的總和 $\le m$,也就是
$\Sigma deg[x] \le m$
而連出去的點必定是輕點,且其deg必定 $\le \sqrt m$
因此用同個方法做的話,複雜度會是 $O(m \sqrt m)$
加上重點後,總複雜度會是 $O(m \sqrt m)$
----
因此重點和輕點可以寫在一起處理
```cpp
for (int x : arr) { // 枚舉所有點
for (int y : G[x]){
vis[y] = 1; //標記
}
for (int y : G[x]) {
for (int z : D[y]) {//直接暴力找
ans += vis[z];
}
}
for (int y : G[x]){
vis[y] = 0; //取消標記
}
}
```
----
可以發現其實把圖轉成 deg 之後,所有長度為 3的環都會長得像右圖。
其中有一個特別重的點連向兩個其他相對輕的點
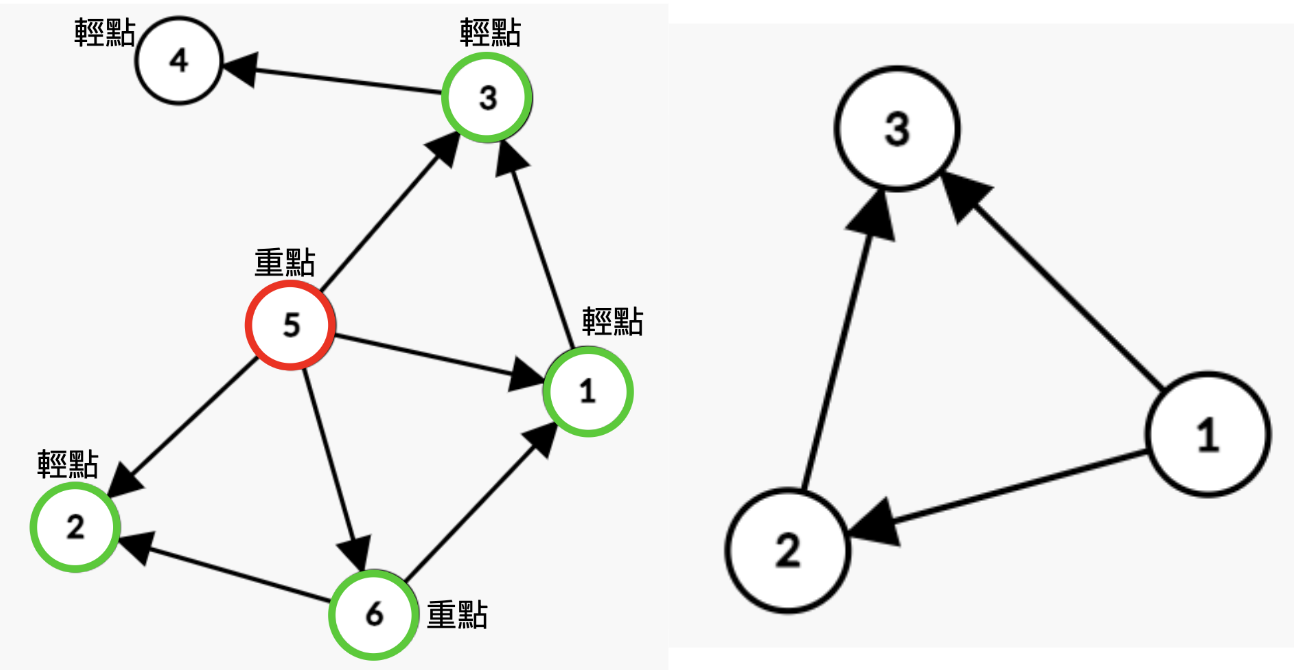
當「枚舉到環上最重的點時」,就會以這個最重的點去計算有幾個環。
----
## 例題3 --- Count rectangles in a graph
給一張 $n$ 個點 $m$ 條邊的簡單無向圖,
求圖上有幾個四邊形 (大小為 4 的環)
$1\le n, m\le 10^5$
下圖答案為 2 (3-5-6-1-3 , 2-5-1-6-2)

----
跟上一題的差別在於要去找長度為 4 的環,以結論來說做法跟上一題相似
我們可以先觀察在有向圖中,長度為 3 和長度為 4 的環有什麼差別
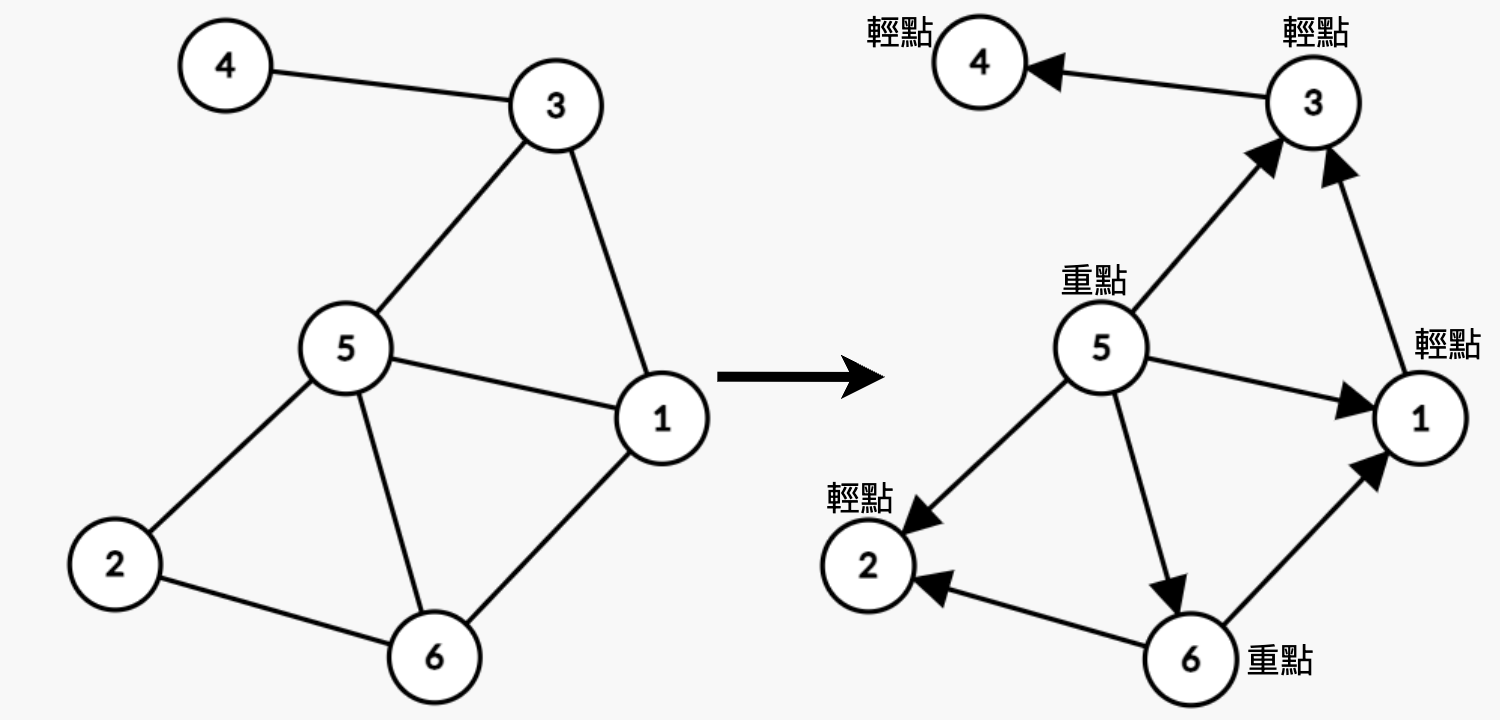
----
## 長度為 4 的環
跟長度為 3 的環一樣,一樣枚舉到環上面最重的點才會去計算環,像下方的點 x
而 x 相鄰的邊一定是連出去的,因此會長下圖的樣子

而不論綠色的邊的方向為何,這張圖都會對答案產生貢獻
----
## 算rectangles in a graph的作法
對於所有點 x,求出以 x 為最重的點,計算環的數量。
- 依序枚舉所有 x 連出去的點 y
- 對於每一個 y 做以下操作
- ans += cnt[z] , z 為當前的 y 連出去的點
- cnt[z]++
- 算完所有 y 的答案之後,對所有 y 連出去的 z 做 cnt[z]-\-
----
- 依序枚舉所有 x 連出去的點 y (<font color="red">當前為 y1</font> )
- 對於每一個 y 做以下操作
- ans += cnt[z] , z 為當前的 y 連出去的點
- cnt[z]++

- ans = 0
----
- 依序枚舉所有 x 連出去的點 y (<font color="red">當前為 y1</font> )
- 對於每一個 y 做以下操作
- <font color="red">ans += cnt[z] , z 為當前的 y 連出去的點</font>
- cnt[z]++

- ans = 0 <font color="red">+ 0 + 0</font>
----
- 依序枚舉所有 x 連出去的點 y (<font color="red">當前為 y1</font> )
- 對於每一個 y 做以下操作
- ans += cnt[z] , z 為當前的 y 連出去的點
- <font color="red">cnt[z]++</font>

- ans = 0 + 0 + 0
----
- 依序枚舉所有 x 連出去的點 y (<font color="red">當前為 y2</font> )
- 對於每一個 y 做以下操作
- ans += cnt[z] , z 為當前的 y 連出去的點
- cnt[z]++

- ans = 0 + 0 + 0
----
- 依序枚舉所有 x 連出去的點 y (<font color="red">當前為 y2</font> )
- 對於每一個 y 做以下操作
- <font color="red">ans += cnt[z]</font> , z 為當前的 y 連出去的點
- cnt[z]++

- ans = 0 + 0 + 0 + <font color="red">1</font>
----
- 依序枚舉所有 x 連出去的點 y (<font color="red">當前為 y2</font> )
- 對於每一個 y 做以下操作
- ans += cnt[z] , z 為當前的 y 連出去的點
- <font color="red">cnt[z]++</font>

- ans = 0 + 0 + 0 + 1
----
- 依序枚舉所有 x 連出去的點 y (<font color="red">當前為 y3</font> )
- 對於每一個 y 做以下操作
- ans += cnt[z] , z 為當前的 y 連出去的點
- cnt[z]++

- ans = 0 + 0 + 0 + 1
----
- 依序枚舉所有 x 連出去的點 y (<font color="red">當前為 y3</font> )
- 對於每一個 y 做以下操作
- <font color="red">ans += cnt[z]</font> , z 為當前的 y 連出去的點
- cnt[z]++

- ans = 0 + 0 + 0 + 1 <font color="red">+ 1 + 2</font>
----
- 依序枚舉所有 x 連出去的點 y (<font color="red">當前為 y3</font> )
- 對於每一個 y 做以下操作
- ans += cnt[z] , z 為當前的 y 連出去的點
- <font color="red">cnt[z]++</font>

- ans = 0 + 0 + 0 + 1 + 1 + 2
----
以 x 來說,枚舉完了,把所有枚舉過的 z 的 cnt 設定為 0

- ans = 0 + 0 + 0 + 1 + 1 + 2 = 4
因此這一張圖有 4 個長度為 4 的環,算完之後再枚舉其他點 x 就好!
----
## 程式碼
```cpp
for (int x : arr) { // 枚舉所有點
for (int y : G[x]){//用DAG枚舉y
for(int z : adj[y]){//用無向邊枚舉點z
ans += cnt[z];
cnt[z] += 1 ;
}
}
for (int y : G[x]){
for(int z : adj[y]){
cnt[z] = 0;//x 枚舉完了,把cnt[z]重置
}
}
}
```
----
## 複雜度?
枚舉複雜度,一樣以重點和輕點枚舉
----
## 複雜度?
對於重點 x 來說,x的數量有 $\sqrt m$ 個
那些 y$_1$,y$_2$,...y$_{deg[x]}$ 的 deg 總和必定 $\le m$
因此重點複雜度會是 $O(m \sqrt m)$

----
## 複雜度?
對於輕點 x 來說,所有 x 連出去的 y 數量總和最多有 $m$ 個
而對於每個 y ,連出去的 z 的數量不會超過 $\sqrt m$個
因此輕點複雜度會是 $O(m \sqrt m)$
總複雜度 $O(m \sqrt m)$
----
## 要注意的小地方

在上圖的情況下
- 枚舉 x1 時,會把 x2 當作 z,對答案貢獻一次
- 枚舉 x2 時,會把 x1 當作 z,又對答案貢獻一次
導致重複算到同一個環
----
在計算答案的時候要保證點 x 一定要比 z 還要重
可以考慮寫一個函式檢查 x 是否比 z 還要重
```cpp
bool check(int x,int z){
return ( deg[x]==deg[z] ? x>z : deg[x]>deg[z] );
}
for (int x : arr) { // 枚舉所有點
for (int y : G[x]){//用DAG枚舉y
for(int z : adj[y]){//用無向邊枚舉點z
if( !check(x, z) )continue;
ans += cnt[z];
cnt[z] += 1 ;
}
}
for (int y : G[x]){
for(int z : adj[y]){
if( !check(x, z) )continue;
cnt[z] = 0;//x 枚舉完了,把cnt[z]重置
}
}
}
```
----
## 結論
很多圖上根號分 case 的題目,
由於邊的數量都是有上限的,可以用 degree 大小來區分,
因此以外看到圖上計算每個節點與相鄰點之間關係的題目,
都可以想一下是否可以分 case 處理
---
## 序列分塊
一種資料結構
用於區間操作,區間詢問之類的問題
----
將序列分成每塊大小為$\lfloor \sqrt{n} \rfloor$,而總共$\lceil \frac{n}{ \lfloor \sqrt{n} \rfloor } \rceil$塊
以 $n=10$ 為例
每塊大小為$\lfloor \sqrt{n} \rfloor = 3$,總共 $\lceil \frac{n}{ \lfloor \sqrt{n} \rfloor } \rceil = 4$ 塊

```cpp=
//分塊結構
//求區間總和
struct blk{
vector<int> local; //每塊的全部元素
int global; //儲存每塊的總和
int tag; //儲存整塊一起更新的值
blk(){ //初始化
local.clear(); //清空區間元素
tag = global = 0; //將區間總和先設為0
}
};
```
----
### 預處理
(求區間總和)

```cpp=
vector<blk> b;
void build(){
int len=sqrt(n),num=(n+len-1)/len;
for(int i=0;i<n;i++){ //第i個元素分在第 i/len 塊
cin>>x;
//存入區間中
b[i/len].local.push_back(x);
//更新區間總和
b[i/len].global += x;
}
}
```
----
### 區間加值
區間 1~9 加值 5

#### 最左塊
最左邊那塊每格暴力跑過去加值
#### 中間每塊
在中間每格的 TAG 加值
#### 最右塊
最右邊那塊每格暴力跑過去加值
----
### 區間加值
<div style="font-size:30px">
假設區間 1~9 加值 5

會發現最右邊那塊裡面每格都有選到
但是為了方便實作,因此最右邊那格會直接暴力加
</div>
----
<div style="font-size:30px">
### 區間加值
(求區間總和)
</div>
<div style="margin-left:-120px">
```cpp=
void update(int ql,int qr,int v){
int blk_l=ql/len,blk_r=qr/len,ret=0;
if(blk_l == blk_r){ //如果都在同一塊直接一個一個跑過去就好
for(int i=ql;i<=qr;i++)
b[blk_l].local[i%len]+=v;
b[blk_l].global+=(qr-ql+1)*v;
return;
}
for(int i=ql;i<(blk_l+1)*len;i++){ //最左的那一塊
b[blk_l].local[i%len]+=v;
b[blk_l].global+=v;
}
for(int i=blk_l+1;i<blk_r;i++){ //中間每塊
b[i].tag+=v;
b[i].global+=v*len;
}
for(int i=blk_r*len;i<=qr;i++){ //最右的那一塊
b[blk_r].local[i%len]+=v;
b[blk_r].global+=v;
}
}
```
</div>
----
### 詢問
(假設要求區間總和)
做法與區間加值相同,分最左、中間每塊、最右
以詢問區間 2-8 為例

----
### 詢問
(求區間總和)
<div style="margin-left:-120px">
```cpp=
int query(int ql,int qr){
int blk_l=ql/len,blk_r=qr/len,ret=0;
if(blk_l == blk_r){ //如果都在同一塊直接一個一個跑過去就好
for(int i=ql;i<=qr;i++)
ret+=b[blk_l].local[i%len]+b[blk_l].tag;
return ret;
}
for(int i=ql;i<(blk_l+1)*len;i++) //最左的那一塊
ret+=b[blk_l].local[i%len]+b[blk_l].tag;
for(int i=blk_l+1;i<blk_r;i++) //中間每塊的總和
ret+=b[i].global;
for(int i=blk_r*len;i<=qr;i++) //最右的那一塊
ret+=b[blk_r].local[i%len]+b[blk_r].tag;
return ret;
}
```
</div>
----
## 複雜度分析
- 建表
$O(n)$, 一個一個跑過去就好
- 更新
最左的那塊裡面最多跑過 $\sqrt{n}$ 格
中間跑過最多 $\sqrt{n}$ 大塊
最右的那塊裡面最多跑過 $\sqrt{n}$ 格
複雜度 $O(\sqrt{n})$
- 詢問
同上
複雜度 $O(\sqrt{n})$
----
### 結論
分塊看起來複雜度比線段樹差
但分塊用迴圈實作常數比較小(線段樹遞迴常數較大)
實際上大部分題目都還是可以過的
$n = 2 \cdot 10^5 , n \sqrt{n} = 89,442,719$
熟悉之後,實作複雜度不比線段樹高
而且能解出更多線段樹解不出來的題目
---
## 莫隊算法(mo's algorithm)
是2009年中國國家代表隊「莫濤」所提出來的
一種運用到分塊概念的離線演算法
----
## 使用條件
用於序列的區間詢問
對於詢問的 $[l,r]$ 區間,如果已經計算好區間內的答案
並且能在 $O(1)$ 或者 $O(\log N)$ 的複雜度內,計算轉移到區間的答案
$[l,r+1], [l,r-1], [l+1,r], [l-1,r]$ (即 $[l,r]$ 左界或右界移動一格)
則可以在$O(N\sqrt{N})$的複雜度內求出所有詢問的答案
----
### 引入問題
[SPOJ-DQUERY](https://www.spoj.com/problems/DQUERY/)
給你一個大小為 $n(n\le3 \cdot 10^4)$ 的序列 $a (1\le a_i\le10^6)$
$q(q\le200000)$ 筆詢問,每次問你區間 $[l,r]$ 內,有幾個不同的數字
如果每次都直接暴力找,最差複雜度 $O(NQ) \rightarrow$ TLE
----
## 作法
將所有詢問分塊之後各自排序,依序暴力從前一個詢問區間計算完答案轉移到下一個詢問區間求出答案
將所有詢問依照先依照左界 $l$ 去分塊,
$\frac{l}{\lfloor\sqrt{n}\rfloor}$ 一樣的在同一塊,而同一塊的分別再各自用右界 $r$ 去排序
```cpp=
int n,k = sqrt(n); //每塊大小為k
struct query{
int l,r,id; //詢問的左界右界 以及 第幾筆詢問
friend bool operator<(const query& lhs,const query& rhs){
return lhs.l/k==rhs.l/k ? lhs.r<rhs.r : lhs.l<rhs.l;
} //先判斷是不是在同一塊 不同塊的話就比較塊的順序,否則比較右界r
};
```
----
### 排序詢問
假設序列長度為 $10 (i \in 0 \sim 9)$ , 每格大小為 $\lfloor\sqrt{10}\rfloor = 3$
詢問有 [4, 8], [2, 3], [9, 9], [0, 7], [1, 2], [6, 9], [7, 8]
將詢問排序 (先比較塊的順序,再比較右界大小)
[1, 2], [2, 3], [0, 7], [4, 8], [7, 8], [6, 9], [9, 9]
----
### 暴力轉移
從前一個區間轉移到下一個區間,每次移動一格
以 區間 [0, 7] 轉移到區間 [4, 8]
[0, 7] $\to$ [0, 8] $\to$ [1, 8] $\to$ [2, 8] $\to$ [3, 8] $\to$ [4, 8]
一次 新增/刪除 一個元素
----
## 暴力轉移
```cpp=
int num = 0;
int cnt[1'000'005], ans[30'005];
vector<query> q;
void add(int index){ ... } //新增元素到區間內並更新數量 num
void sub(int index){ ... } //從區間內移除元素並更新數量 num
void solve(){
sort(q.begin(),q.end());
for(int i=0,l=0,r=-1;i<n;i++){
while(l>q[i].l) add(--l);
while(r<q[i].r) add(++r); //記得要先做新增元素的
while(l<q[i].l) sub(l++); //再做移除元素的
while(r>q[i].r) sub(r--);
ans[q[i].id] = num; //移到區間後儲存答案
} }
```
----
#### 計算新增/刪除元素
不同題目新增/移除元素做法不同,以例題來說
給你一個大小為 $n(n\le3 \cdot 10^4)$ 的序列 $a (1\le a_i\le10^6)$
每次問你區間 $[l,r]$ 內,有幾個不同的數字 ?
直接開一個值域大小的陣列 cnt[1000005],計算每個數字出現的次數
新增元素 add(x) 直接 cnt[x]+=1,並且判斷是不是原本為 0 ,若為 0 則個數 +1
移除元素 sub(x) 則為 cnt[x]-=1,移除後判斷是否變為 0 ,若為 0 則個數 -1
每次更新複雜度 $O(1)$
----
#### 計算新增/刪除元素
```cpp=
void add(int x){
++cnt[x];
if(cnt[x] == 1) ++num;
}
void sub(int x){
--cnt[x];
if(cnt[x] == 0) --num;
}
```
----
## 複雜度分析
$n$ 為序列總長度,
$q$ 為詢問比數,
$p$ 為移動一格的複雜度
#### 左界
:::info
在同一塊裡,每次移動量最多為 $\sqrt{n}$,
不同塊之間距離總和最多為 $n$
因此移動總量為 $q\sqrt{n} + n$
:::
#### 右界
:::info
每塊裡面是遞增的,因此每塊裡面最多移動 $n$,有 $\sqrt{n}$ 塊
而不同塊之間最多移動 $n$
:::
移動加起來為 $q\sqrt{n} + n\sqrt{n} + n$
複雜度為 $O(p(q+n)\sqrt{n})$
----
## 其他優化
排序的時候,在同一塊的詢問區間會用右界排序
而把相鄰分塊的右界大小關係交替 (小於$\to$大於$\to$小於$\to$大於)
就能省去一些常數的時間
 
```cpp=
bool operator<(const query &lhs, const query &rhs){
if(lhs.l/k!=rhs.l/k) return lhs.l/k<rhs.l/k;
return ((lhs.l/k)&1?lhs.r<rhs.r:lhs.r>rhs.r); // 奇數塊右界遞增,偶數塊右界遞減之類
}
```
---
## 常數優化
通常分塊、根號的題目的分塊大小會用常數決定,
常見的大小會設成 400, 450, 500 等等
```cpp=
const int k = 400;
```
而不是由輸入的大小決定
```cpp=
int k = sqrt(n);
```
使用常數宣告的方法常數通常會比較小
很多時候分塊 TLE 的時候也會直接調整分塊大小來避免一些特別產的測資
大家可以測試看看分塊大小不同的速度差別
----
## 作業
deadline: 2 week
https://vjudge.net/contest/661404#overview
{"title":"Sqrt-Decomposition","description":"Sqrt-Decomposition on Math","contributors":"[{\"id\":\"08326fa4-ca9b-4ca9-873e-239ebe76662c\",\"add\":25840,\"del\":8372}]"}