# More NAHD QCs

###### tags: `SoftQC` `self-assembly`
---

## Infinite pressure phase diagram for spheres on a plane

This is the phase diagram at infinite pressure for NAHD with $\Delta = \Delta_{plan}$ such that equivalent 3D spheres lie on a plane.
*This phase diagram does not include S4, which I could not tame (nasty NaNs).*


## Reminder for phases


Non-additivity parameter (could choose to change sign):
>[Frank]: Since you see the S4 phase in our JCP only for size ratios $q < 0.2$ and nonadditivity $\Delta > -0.05$, I think it is reasonable to conclude it is not a concern for this diagram?

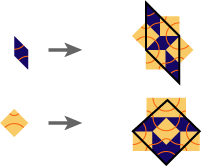
## Infinite pressure unit cells

||S1|S2|T1|H1|
|:-:|:-:|:-:|:-:|:-:|
|$q=0.40$|||||
|$q=0.45$|||||
|$q=0.50$|||||
|$q=0.55$|||||
|$q=0.60$|||||

## Tiles edge length at infinite pressure

The following figure displays the edge length of the tiles at infinite pressure as a function of size ratio, for spheres-on-plane configuration.
For T1 and H1, the tiles are triangles (half unit cell). Most unit cells have a short and a long edge.


Black ellipses loosely identify matching regions in which tiles edges are of comparable length, and tiling them might be possible. The black crosses identify the points at which squares are undeformed (not rectangles nor rhombi).
* QC12 is formed of squares and equilateral triangles of unit length.
* QC8a requires small edge of triangles (T1 or H1) to match the S1 edge.
* QC8b requires long edge of triangles to match the S2 edge.

[14/01/22]

The following figure is an update of the previous one, where T1 was removed in favour of H1. The symmetric expansion of the squares was added for S1 and S2 (dotted lines) and the top plot represents the acute angle of the H1 triangles. The blue cross highlights the angle of $2\pi / 8$.


Remarkably, the triangles can form perfect octagons at $q = 0.5$. At this size ratio, S1 squares are also perfect squares . Therefore, the QC8b phase should exist even in the tightly constraint regime of infinite pressure.

QC8a requires finite pressure since whenever S2 is a square and matches the long edge lenght of the triangles, the triangles acute angle is smaller than $2\pi / 8$.
However, the symmetric expansion of S2 has very similar edge length than the triangles for all size ratios. Hence, it is not surprising that QC8a exists at finite pressure.

## Self-assembled phases

|Label|State point|Snapshot after $10^6$ time units|Scattering pattern|
|:-:|:-:|:-:|:-|
|QC12|$q=0.45,x_L=0.65,\eta=0.84$|||
|QC8b|$q=0.45,x_L=0.35,\eta=0.88$|||
|QC8a|$q=0.55,x_L=0.3,\eta=0.84$|||
|S1|$q=0.45,x_L=0.5,\eta=0.87$|||
|S3|$q=0.35,x_L=0.2,\eta=0.96$|||
|T1|$q=0.35,x_L=0.35,\eta=0.96$|||
|H2|$q=0.65,x_L=0.45,\eta=0.81$|||

### Some thoughts...

- **Square-triangle QC:** This shows up in simulations for size ratios 0.4, 0.45, and 0.5. This is indeed close to the area where the infinite-pressure phase diagram predicts a S1-Hex coexistence (and hence a random tiling is possible).

- **Octagonal QC with small squares:** This also shows up in simulations for size ratios 0.4, 0.45, and 0.5. Since this is a combination of S1-tiles and H1-tiles, it could be considered surprising that H1 is not stable here at infinite pressure (it's T1 instead). However, I could imagine that H1 might be close in terms of packing.

- **Octagonal QC with big squares:** This shows up for size ratios 0.55, 0.6. This is a combination of S2-tiles (mostly in pairs of two joined at the short side) and H1-tiles. Indeed, this region is close to the region where both of these are stable at infinite pressure. Since the infinite pressure diagram shows S2 to be stable in several distinct regions over a wide range of size ratios, I'm guessing it probably still packs quite well for the rest of the region $0.5<q<0.6$.

- **S3** looks a bit different from the picture, since we see it self-assemble at a fairly high size-ratio, but I think that is the same phase, right?
>[Etienne]: Looks like S3 to me too, although the S3 composition would be $x_L = 1/6$. At $x_L = 0.2$, there is an excess of large spheres which seem to be absorbed in T4 and S2 units.
>[Frank]: The same phase can be seen at $x_L = 0.15$, although then there are clearly some regions witch excess small particles.

- Depending on composition, **T1** tends to show a lot of defects (missing small particles), which is reminiscent of the interstitial solid solution you get when making NaCl crystals in 3D. See: https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.107.168302?casa_token=5fWVGdCACGMAAAAA%3AbW2WUw25GBIpEtKDLThXqAzvyfNNTezWx_lThSzWIy4bzbBF-mitB7By1_IBZaRtEwLk0kUEKYaM7Q Note that like T1, NaCl is also just a combination of the densest-packed crystal for the large spheres, with small spheres in the holes.
>[Etienne] Yep, that's what Likos and Henley call a "lattice gas" at infinite pressure (dotted regions in the phase diagram).
>[Frank]: True

- I don't really see a pure **H2** phase, but I do see small patches of it for high size ratios (~0.6) at compositions near 0.5. Those systems also still seem to be rearranging. I am running the state points where the pressure is reasonable for longer now. (Reasonable pressure defined as $17<\beta P \langle \sigma^2 \rangle < 31$, this seems to roughly cover the state points that are not jammed or clearly just fluid.)
Update on this: Running longer does yield slightly larger patches of H2 in various systems close to the expected size ratio and composition, but self-assembly seems very slow. The figure in the table is probably the best example...

Perhaps it would be nice to make a plot with the maximum packing fractions of the most relevant structures (at least S1, H1, S2, T1) as a function of $q$ to illustrate the regions where these phases are packing well (if not "best")?

>[Etienne] Here it is. Note that the phases don't have the same composition, so the packing fraction comparisons cannot be brought too far.
>[Frank]: Good point. Still nice to have an impression, but comparisons are indeed tough to make.


## Self-assembly diagram
For each $q$ and $x_S$, we indicate what phases self-assemble (at any packing fraction). Even phases that are only present in part of the simulation box are counted (e.g. H2). Overlapping regions indicate either coexisting/competing phases or different phases at different packing fractions. The label "hexLplus" indicates a hexagonal crystal of large disks with small ones interspersed. This includes the T1 phase, as well as as messier phases that include e.g. S3, S5, T1, T2, T4 tiles. Note that S3 itself is clearly distinct from this, at it has rhombic symmetry, not hexagonal.


## Picture of a larger octagonal QC with small squares with bonds:

Long bonds are red, short bonds are blue.


## Tilings

The quasicrystals we observe can be viewed as decorated tilings. When tiles permit random tiling of the plane, a random tiling QC will be obtained because of the finite configurational entropy.
Random tilings are often related to ideal tilings formed of the same prototiles. Properties of the ideal tiling (eg. proportion of tiles of each type, global symmetry...) are preserved in the random realisations. As such, it is useful to identify the ideal tilings related to our random tiling QC.

### QC8b

8-fold symmetric QC comprised of squares and isoceles triangles. The **short** edges of the triangles match the edges of the squares. Squares are S1 unit cells and triangles are H1 half unit cells.

#### Self-assembled tiling


The defects that appear in the tiling are:
* Pentagons containing about 3 small particles
* S2 squares
* HexL triangles

#### Random tiling model

We construct tiles by joining the centres of neighbouring large disks.

Accounting for the different orientations, there are 2 squares and 8 triangles.
Let $a$ be the edge length of the squares. Then, the long edge length of the triangles is $\sqrt{1 + 1/\sqrt{2}}\;a \simeq 1.307 a$.

It is possible to construct two different octagonal clusters around the two squares, which have the same boundary. Moreover, one can construct tilings with a finite concentration of those clusters. Hence, the number of tiling configurations grows exponentially in the size of the tiling.

The following figure depicts the tiles, the two octagonal clusters, and a configuration with a finite concentration of them.


Moreover, several distinct tilings can be constructed from those tiles. The following figure displays 3 such periodic structures.


Together, those two points qualify this tiling as a random tiling model, according to the definition provided by Henley in *Quasicrystals: The state of the art*.

This however gives us no clues about a possible zero phason strain tiling, nor about the average symmetry of such tilings.

In spite quite some of efforts, I could not identify inflation rules to generate highly symmetric, non periodic tilings. In particular, I could not find a proper substitution for the triangles.

QC8b is equivalent to the tiling found by Thomas. One can continuously transform one into the other. The last column of the next figure is a reproduction of a part of Thomas tiling with our tiles.

||||
|:-:|:-:|:-:|

#### Lifting

Here I propose a lifting basis build from the procedure outlined by Henley in *Quasicrystals: The state of the art*.

* Use tiles edge orientation to guess a parallel projection of the high dimensional lift basis $\{e_i^\parallel\}_{i=0}^{D}$.
* Make sure that the chosen vectors allow to index all points in the tiling in a *unique* way (up to origin choice), and that vectors sum to 0 around a closed loop.
* Make sure that no extra vector can be added while still satisfying the above constraints. If so, include the extra vector to the basis.
* Construct the perpendicular projections of the lift basis $\{e_i^\perp\}_{i=0}^{D}$ from parallel space symmetries.
* Construct the lift basis $\{e_i\}_{i=0}^{D}$ from the parallel and perpendicular projections.

We start by looking at the orientation of the tiles edges. The edges of the triangles follow the 8 directions of a regular octagon. We chose 4 of them as the parallel projections of the --supposedly-- 4D lift basis vectors. The other 4 are simply minus the chosen ones (see next figure).

Note that the edges of the squares are sum and differences of the projected basis.


The sum of the vector around any tile is zero, and thus around any closed path.

We then need to construct the perpendicular projections of the 4D lift vectors. Consider the transformation of the parallel projections under a rotation of $\pi / 4$: $e_0^\parallel \rightarrow e_1^\parallel$, $e_1^\parallel \rightarrow e_2^\parallel$, $e_2^\parallel \rightarrow e_3^\parallel$, $e_3^\parallel \rightarrow - e_0^\parallel$.
The rotation by $\pi/4$ in the parallel subspace corresponds to a more general transformation in the high dimensional lift space, and must thus correspond to another transformation in the perpendicular space. Thus, to find the perpendicular projections, we look for another transformation that results in the same permutation. Rotations by $3\pi / 4$ realize this.

Without loss of generality, we fix $e_0^\perp = (l, 0)$. $e_1^\perp$ is obtained by applying a first rotation of $3 \pi / 4$, then $e_2^\perp$ and finally $e_3^\perp$. Note that applying again the rotation to $e_3^\perp$ gives $-e_0^\perp$, as we wanted to match the permutation realized in parallel space by rotations of $\pi / 4$ (see figure above).

Now, we can simply construct the 4D lift basis from the projections. The simplest choice is to encode the parallel space on the first two coordinates, and the perpendicular space on the las two ones, *ie.* $E^\parallel = Vect((1, 0, 0, 0), (0, 1, 0, 0))$ and $E^\perp = Vect((0, 0, 1, 0), (0, 0, 0, 1))$.

$$
e_0 = \left(l, 0, l, 0\right) \\
e_1 = \left(l \frac{\sqrt{2}}{2}, l \frac{\sqrt{2}}{2}, -l \frac{\sqrt{2}}{2}, l \frac{\sqrt{2}}{2}\right) \\
e_2 = \left(0, l, 0, -l\right) \\
e_3 = \left(-l \frac{\sqrt{2}}{2}, l \frac{\sqrt{2}}{2}, l \frac{\sqrt{2}}{2}, l \frac{\sqrt{2}}{2}\right)
$$

These 4 vectors are linearly independent, as they should.

Using this basis, it is possible to index a tiling of the QC8b family with four integer indices. The following figure displays the parallel and perpendicular space representations of a simple octagonal cluster.

||
|:-:|:-:|
|Parallel space projection of an octagon cluster.|Perpendicular projection obtained from the above lift basis.|

### QC8a

8-fold symmetric QC comprised of squares and isoceles triangles. The **long** edges of the triangles match the edges of the squares. Squares are S2 unit cells and triangles are H1 half unit cells.

### Ammann-Beenker tiling

https://tilings.math.uni-bielefeld.de/substitution/ammann-beenker/

|||
|:-:|:-:|

The ratio of number of squares over number of rhombi is $n_{sq} / n_{rh} = \sqrt{2} / 2$

### Watanabe-Ito-Soma tiling

https://tilings.math.uni-bielefeld.de/substitution/watanabe-ito-soma-8-fold/

|||
|:-:|:-:|

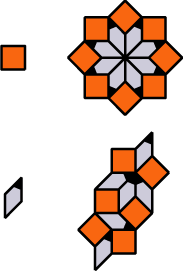The ratio of number of squares over number of rhombi is $n_{sq} / n_{rh} = \sqrt{2} / 2$, as for Ammann-Beenker tiling.

>[Frank]: A rhombus tile is the same as in T1: it consists of 1 large disk and 2 small disks (only counting the parts of particles within the tile). A large square is the same as in S2, so 4 small disks and 1 large disk. The number of large particles is $N_L = n_{sq}+n_{rh}$, and the number of small particles is $N_S = 4n_{sq} + 2 n_{rh}$. Hence, I think the ideal composition should be $x_L = (2 \sqrt{2} - 1)/7 \simeq 0.2612$ (NOTE: this is wrong, see below). In practice, we see quite a bit of demixing at $x_L = 0.25$, so not sure this carries over very well.
>[Etienne]: I did the same calculation but arrived at $x_L = (1 + \sqrt{2}) / (3 + 5\sqrt{2}) \simeq 0.2397$. Your result looks nicer but I couldn't find a mistake in my calculation :/. It is in the same range though and, you observe demixing anyway. Interestingly, this means that we observe the QC with an excess of large disks this time, right ?
>[Frank]: I recalculated, and agree with you.

Ammann-Beenker and Watanabe-Ito-Soma tiling are different however. This can be seen by remarking that the latter contains some square-square-square-rhomb-rhomb vertices which are forbidden in the former (see Baake and Joseph 1990).

In our case, we don't care that much because we will get a random tiling anyway, and there infinitesimal chance that an entropy difference could be measured between the two ;).

This tiling might also be interesting: https://tilings.math.uni-bielefeld.de/substitution/rhomb-square-octagon/.

## Mapping the quasicrystals?

It seems that configurations of the QC8b (with small squares) can be mapped to configurations of QC8a (with large squares, Ammann-Beenker-like), as illustrated below:


Basically, each long edge gets replaced by a rhombus, and each short edge by a square.

## Tiling analysis

Here we analyse the tiling using the underlying tiling.

We use a 2k particles system at size ratio $q = 0.45$, composition $x_S = 0.65$ and packing fraction $\eta = 0.88$.

We consider the bonds between large particles. The bond angle and length distribution show that long and short bonds can be discriminated, and ideal symmetry angles can be identified.

|||
|:-:|:-:|
|Bond length distribution. There are clearly two families corresponding to short and long bonds.| Bond angle distribution. 8 + 8 ideal angles can be identified.

The tiles are reconstructed from the cycles in the bond network. Angles and edge lengths are used to associate the tiles to the 10 prototiles that comprise the QC8b tiling (2 squares, and 8 triangles).

|||
|:-:|:-:|
|Tiles abundance per type.| Reconstructed tiles. White, black and pink tiles are considered defects.|

The 2 types of squares and the 8 types of triangles appear with roughly the same proportions, which is likely a signature of the maximally random tiling that certainly possesses the 8-fold symmetry.
In the above tiling, $N_{sq} / N_{tr} = 78 / 877 \approx 0.0889$. This value is close to $\sqrt{2} / 16 \approx 0.0883$ (not a strong claim on the ideal composition at all of course !).

The proportion of defect tiles is also quite high. Noticeably, we observe large squares that are units of the QC8a tiling, and small equilateral triangles that form the QC12.

Once ideal tiles are identified, one can lift the tiling using the 4D representation.

|||
|:-:|:-:|
|||
|Reconstructed ideal tilings for two different starting tiles.|Perpendicular projections of the lifted tilings.|

The tiles are indexed recursively. The starting tile changes the result of the tiling.
In perpendicular space, points are more concentrated around the origin. We could try looking at larger and larger portions of tiling to see whether the extension in perp space grows logarithmically.

The next figures are the result of the same analysis for a 10k system at a slightly different size ratio of $q = 0.457$.

|||
|:-:|:-:|
|||
|||

### Scans

The following figures display various tiling properties for composition and packing fraction scans at different size ratios.

* $q = 0.5$, $N = 10k$

|||
|:-:|:-:|
|Fraction of defect tiles.|Fraction of square tiles in the good tiles.|
|||
|Fraction of the large and small squares in the good tiles.|Global bond-order parameter $q_8$ (dashed lines are $q_4$)|

>[Frank] The dip for the bond order in the green line is caused by the existence of two domains in the snapshot. Shown is the $q_8$ for the long bonds. The results for the short bonds are essentially the same (slightly higher numbers overall; they go up to 0.8).

|$x_L = 0.275$, $\eta = 0.86$|$x_L = 0.3$, $\eta = 0.86$|$x_L = 0.325$, $\eta = 0.86$|
|:-:|:-:|:-:|
||||
||||
||||

* $q = 0.55$, $N = 10k$

|||
|:-:|:-:|
|Fraction of defect tiles.|Fraction of square tiles in the good tiles.|
|||
|Fraction of the large and small squares in the good tiles.|Global bond-order parameter $q_8$ (dashed lines are $q_4$)|

|$x_L = 0.285$, $\eta = 0.84$|$x_L = 0.32$, $\eta = 0.84$|$x_L = 0.35$, $\eta = 0.85$|
|:-:|:-:|:-:|
||||
|||
|||

Possible next options:
* Explore tiling expansion in perp space with a growing window.
* Identify defect points in the ideal tiling.

## Constraint on tile concentrations
Following Marianne's notebook, the "Nienhuis" relation for the QC8 would be:
$\Sigma + (3 + 2\sqrt{2})\sigma - \tau =\\ (\Sigma_1 - \Sigma_2)^2 + (3+2\sqrt{2})(\sigma_1 - \sigma_2)^2 - \tau^2 + (2+2\sqrt{2})(\tau_1 - \tau_2 + \tau_3 - \tau_4)(\sigma_1 - \sigma_2) + 8(\tau_1\tau_3 + \tau_2 \tau_4)$

If we impose zero phason strain, the right-hand side becomes zero, resulting in:
$\Sigma + (3 + 2\sqrt{2})\sigma - \tau = 0$
Imposing zero phason strain also yields four constraints due to the hyperslope-matrix B vanishing:
$\Sigma_1 = \Sigma_2$
$\tau_1 = \tau_3$
$\tau_2 = \tau_4$
$\sigma_1 - \sigma_2 = 2\frac{\tau_2-\tau_1}{1+\sqrt{2}}$
Together with the requirement that $\Sigma + \sigma + \tau = 1$, this leaves two degrees of freedom. For example, we can choose $\sigma$ to be anywhere between $0$ and $(2-\sqrt{2})/4 \simeq 0.146$, and then still have freedom in the choice of $\sigma_1 - \sigma_2$, which I think can vary between $-\sigma$ and $\sigma$. Both degrees of freedom can be sampled by local rearrangements of an octagonal region:


All three configurations above contain a full set of 8 differently oriented triangles. Additionally, A contains an S1 and an S2 square, B contains an s1 square and one each of t2, t4, t6, t8 triangles, and C contains an s2 square and one each of t1, t3, t5, t7 triangles.
Switching from A and either B or C increases $\Sigma$ at the expense of $\sigma$, while switching between B and C changes the relative concentrations $\sigma_1$ and $\sigma_2$. Since these moves are local, they do not affect the global phason strain.

Note that additionally imposing 8-fold average symmetry fixes $\sigma_1 = \sigma_2$, and hence $\tau_1 = \tau_2$.

## Inflation scheme

While drawing a figure for the thesis, I found a promising lead to an inflation scheme for the QC8.


The vertices of the next inflation step are located in the center of octagonal clusters, which can appear in two orientations. This imposes matching rules on the supertiles.


The new supertiles contain fragments of squares and triangles that account for irrational fractions of the original tiles.


Knowing the contribution of the fragments, we can derive how many of each types of tile a tile in the original tiling generates after inflation. For the squares, the number of tiles in the supertiles is independant on the orientation of the octagonal clusters at the vertices. For the triangles, the orientation of the clusters matters.


For small squares and triangles, the edge configuration fully determines the interior of the supertile. For large squares however, one can still freely chose a central octagonal cluster.


In fact, one could also use the octagonal clusters based on large squares for the vertices of the supertiles. That would add even more possibilities to the ones already presented. It seems that there is a little bit too much freedom here...
We could try imposing certain symmetries (eg. self-similarity ?) and see if it provides a well defined inflation scheme. Then, using the expressions above, it is easy to compute the composition of the tiling after an infinite number of inflation steps.

## Literature

### Reviews

* Dotera, Isr. J. Chem. **51**, 1197-1205 (2011): The classical review on soft QC. It's already 10 years old now, but I don't think there is a more recent one.

### QC in experiments

* Wang et al., Phys. Rev. Lett., **9** 1010-1013 (1987): First experimental observation of QC8 in an alloy (Ammann-Beenker type).
* Zeng et al., Nature, **428** 157-160 (2004), Talapin et al., Nature, **461** 964-967 (2009): Dodecagonal QC in soft matter experiments.
>[Etienne] No QC8 in soft matter experiments so far, as far as I can tell.

### QC in simulations

* Widom et al. (1987): QC10 in 2D binary LJ mixture.
* Dotera et al. (2014): QC10/12/18/24 in monodisperse HCSS.

* Damasceno et al., J. Phys.: Condens. Matter **29**, 234005 (2017): Supposedly the first QC8 found in simulation. MD study of 3D systems of monodisperse particles interacting via an oscillating potential forged from the g(r) of the diamond structure. An iQC, QC12, QC10 and QC8 are found. QC8 corresponds to a decoration of the Ammann-Beenker tiling resembling the $\beta$-Mn structure. Model for atomic systems, not soft.
* Zu et al., Nat. Commun. **8**, 2089 (2017): QC8 and QC12 found in monodisperse system of soft repulsive core particles. Authors emphasize the simplicity of the potential, and the absence of built-in QC length scales in it. QC8 is a decorated Ammann-Beenker tiling with pentagonal clusters.
* Gemeinhardt et al., EPL, **3** 38001 (2019): metastable QC8 and QC10 in patchy particle system. QC8 is Ammann-Beenker tiling, and harder to form than QC10.
* Malescio and Sciortino, J. Mol. Liq., 118209 (2021): octagonal QC found in a system of monodisperse particle interacting with a short range attraction and Gaussian core. The tiling analysis is rather sparse, but I believe the structure is very close to the one observed by Zu et al. (potentials are relatively close). Authors also find QC18 and QC12.

* Noya, E. G., Wong, C. K., Llombart, P. & Doye, J. P. K. How to design an icosahedral quasicrystal through directional bonding. Nature **596**, 367–371 (2021).
Self assembly of body-centred-cubic and primitive iQC in patchy particles mixtures. The mixtures can be simplified to 2 components in both cases. Authors argue that this could be realised with DNA origami and show that an icosahedral cluster form in MD oxDNA simulations of 70 origami particles (~500 000 nucleotides).
Both approximant and QC structures have inevitable dangling bonds, but QC have more, making the approximant more energetically favourable. However, iQC come with more entropy. Direct coexistence simulations were unconclusive about the relative stability of iQC and approximants.
Note : attractive interactions allow to self-assembly in a fluid without PBC.  
Author used MC simulations, paralellised on GPUs. A fluid at low temperature with~20k particles is first simulated until a nucleus of ~10k particles form. Then this nucleus is inserted in a box of 100k dilute particles at higher temperature to continue growth while preventing other nuclei to form. Final self-assembled QC contain ~70k particles. The composition of the second system does not need to match exactly the nucleus composition for growth to continue

* Leung, P. W., Henley, C. L. & Chester, G. V. Dodecagonal order in a two-dimensional Lennard-Jones system. Phys. Rev. B **39**, 446–458 (1989).
Yet another remarkable paper: they do much more than most more recent papers (including ours) with only 400 particles simulations.
MC study of a binary mixture of LJ particles forming a RTQC12. Small particles are only included to stabilise squares (as in our NAHD mixtures). Hard walls are used in the simulation (~400 particles) and the QC forms in coexistence with the fluid. This free boundary helps annealing the defects, along with long range moves.
Authors remark that the transition is rather continuous, and that the QC order seems to emerge diffusely as temperature is decreased, rather than following a nucleation-growth scenario.
A simple method for identifying disclinations is proposed, that works without having to reconstruct the ideal tiling. Pairs of disclinations form dislocations from which Burgers vectors can be computed.
Determination of the phason strain is performed both fitting the lifted coordinates and using the position of the Bragg peaks in the diffraction pattern.
The conclusion contains an interesting discussion on the possible nature of the quasicrystallisation transition.
In appendix, 3 different arguments are given for the composition of the dodecagonal tiling, along with the derivation of the formula for calculating the phason strain from diffraction peaks.

### Hardish disks

* Likos and Henley, Philos. Mag. B, **68** 85-113 (1993): infinite pressure phase diagram of HD, including QC12.

* Hopkins et al., Phys. Rev. E, **85** 021130 (2012): Infinite pressure phase diagram of binary HS in 3D. Like in 2D, a whole zoo of phases is found, but no QC reported.

* Our paper: Infinite pressure phase diagram of NAHD, including QC12s. Although not required, non-additivity favours quasicrystalline order.

>[Etienne] I could not find studies of solid structures in NAHD mixtures with reasonable keywords on scholar, nor in any paper citing Likos and Henley. People either focus on symmetric NAHD (ie. q = 1) or look at the fluid-solid transition, without much interest for the solid phase.
> It seems that the closest match is the following paper.

* Salgado-Blanco and Mendoza, Soft Matter, **11** 889 (2015): MC study of a weird system of "mushroom shaped particles (sic)" that can be interpreted as binary non-additive hard disks, supplemented with a narrow attractive well. Authors use it to "engineer" structures. They find a dodecagonal QC for a certain set of parameters, which, if I translated correctly, would correspond to $q = 0.58$ and $\Delta = -0.375$ in our language. Note that the value of the non-additivity is ridiculously large in magnitude compared to $\Delta_{plan} = -0.036$ for spheres on a plane at this size ratio. The structure can be seen in fig. 6. Note that the blue particles that comprise the square triangle tiling are actually the big ones (they would cover the small ones if drawn at their real size with these parameters). The decoration of squares and triangles if very different from our own.

### Tilings

* Watanabe et al., Acta. Cryst. A **43**, 133-134 (1987): First description of the substitution rule for Watanabe-Ito-Soma 8-fold tiling.
* Baake and Joseph, Phys. Rev. B **42,** 8091-8102 (1990): rather mathematical analysis of the octagonal tilings of the Ammann-Beenker family. Reports allowed vertex types with their frequency, as well as forbidden ones.

* Fernique and Galanov, ArXiV 2201.00789 (2022): Local growth rules for a "Golden octagonal" tiling. Relation to Ammann-Beenker/Watanabe-Ito-Soma tiling is unclear, but it might be nice to contact Thomas and chat with him. I also don't know the connection with its ternary packing that looks like a good candidate for octagonal tiling. (https://arxiv.org/pdf/2201.00789.pdf)

### Miscelaneous

* LaCour et al., arXiv:2112.06100 [cond-mat]: structures in binary mixtures may be more easily assembled off-stoichiometry, towards more small particles.

## Reply to referees
[05/05/2022]

Referees want more convincing evidence that what we are seeing is indeed a quasicrystal.

We propose will run larger/longer simulations and measure:

* the scaling of the Bragg peaks intensities and width
* the scaling of the extent of the tiling in perpendicular space

Referees also ask for a better characterisation of defects.

### Defects

To see whether defects are point-like are disclination lines, the following figures shows the ideal tiling identified various system, only drawing bonds with a correct length. The current procedure for indexing tiling vertices is recursive and starts from a random vertex. This results in slightly different lifts each time.

$N = 10^4$, $q = 0.5$, $x_S = 0.675$, $\eta = 0.86$
|||||
|:-:|:-:|:-:|:-:|

$N = 10^4$, $q = 0.55$, $x_S = 0.715$, $\eta = 0.84$
|||||
|:-:|:-:|:-:|:-:|

Both point-like and 1D defects are present.
The line defects look very similar to the "tears" observed in a nice toy growth model for square-triangle random-tiling QC [Joseph and Elser, Phys. Rev. Lett **6**, 1066-1069 (1997)].


Joseph and Elser rationalise the tears as "bendings" of the representative surface in 4D.


[10/05/2022]

In order to get a better idea of how vertices are indexed by the recursive procedure, I color points according to the "time" they are indexed. For two different starting vertices, we get:

|||
|:-:|:-:|
|||

The current recursive algorithm indexes vertices radially from the starting point. Tears seem to develop perpendicular to the progressing indexing front. Since the front propagation is homogeneous across the various branches, this coloring scheme doesn't help much in distinguishing them in perp space.

Coloring the vertices according to their distance to the origin in perpendicular space instead yields

|||
|:-:|:-:|
|||

Most of the tiling remains close to the origin. The points further away in perpendicular space correspond to well identified branches. This is very much consistent with Elser and Joseph picture (see above).

Note that in the analysis, I ignore periodic boundary conditions and simply cut the tiling at the box boundaries. It is not clear how one would index the vertices with the periodic boundaries.

[13/05/2022]

In order to allow for possibly better indexing of vertices prevented by the periodic boundary conditions, I ran the same analysis after replicating the system periodically 4 times.

|||
|:-:|:-:|

It is hard to say if the situation is really improved, because the color scale is also affected.

In a QC, when looking at larger and larger windows in parallel space, we expect sublinear scaling of the spread of perpendicular space.
Taking larger and larger windows on the tiling, I compute the distribution of the coordinates of the points in perp space and estimate the spread as the standard deviation of a fitted Gaussian. Since the origin is not necessarily the "true" centre of the perpendicular space cloud, I subtract to $x_\perp$ and $y_\perp$ coordinates the average coordinates of the points in the window. $l$ is the edge length of the small squares in the reconstructed tilings.

||||
|:-:|:-:|:-:|
|Growing observation windows on the tiling replicated 4 times.|Centered distribution of $x_\perp$ and $y_\perp$ coordinates in the windows.|Standard deviation of the fitted Gaussian as function of window radius.|

Significant deviations from gaussian are observed with large windows.
The scaling of the spread in perp-space looks rather linear to me...

Moving the window away from the indexin starting point improves a bit the scaling for short ranges.
|||
|:-:|:-:|

This suggests to me that out tiling is closer to a QC approximant with characteristic a length of about $10 l$.

The tiling dominated by large squares seems to exhibit a better QC order. Although windows go beyond the tiling extent, I think the analysis is still valid to some extent.

||||
|:-:|:-:|:-:|

This tiling is in coexistence with a fluid. This might have helped it anneal its defects. This suggests that the best QC order might be found in simulations with fluid, which I used to consider as less good. I will look for possible better QC there.

[18/05/2022]
Back to $N = 10^4$, $q = 0.5$, $x_S = 0.675$, $\eta = 0.86$, one can get better results by cherry picking the starting point of the indexing, and the centre of the measurement windows, even without replicating the system.
Here indexing start from tile 3414 and measurement windows are centered around (12, -8).

|||
|:-:|:-:|

[09/06/2022]

The systems equilibrated for longer seem to be of better quality.
At $N = 10^4$, $q = 0.5$, $x_S = 0.675$, $\eta = 0.86$:

||||
|:-:|:-:|:-:|

I tried fitting the measured phason strain with power law and log ($f(x) = \alpha \ln(x) +\beta$).
The exponent of the power law fit it smaller than one, and the log fit seems quite good.


### Perpendicular strain
[06/10/2022]

We reproduce analysis of perpendicular strain performed in eg. Je et. al., Proc. Natl. Acad. Sci. U.S.A. **118**, e2011799118 (2021).

The perpendicular displacement field is defined as:

$$
r^\perp (r^\parallel) = \langle d^\perp \vert r^\parallel - \delta / 2 < d^\parallel < r^\parallel + \delta / 2 \rangle
$$

The average is taken over all pairs of particles separated by a distance $d^\parallel$ in parallel space. I use a bin width of $\delta = 1 \sigma_{LL}$.

The perpendicular strain is a $2 \times 2$ matrix. By fitting the perpendicular displacement field with a straight line and measuring the slope, we obtain an average perpendicular strain equal to $\sqrt{\xi_1^2 + \xi_2^2}$ where $\xi_{1, 2}$ are the two eigenvalues of the full perpendicular strain.

* $N = 10^4$, $q = 0.55$, $x_S = 0.715$, $\eta = 0.84$

||||
|:-:|:-:|:-:|

Perp strain $\approx 0.126$, but overestimated in this fit.

* $N = 10^4$, $q = 0.5$, $x_S = 0.675$, $\eta = 0.86$

||||
|:-:|:-:|:-:|

Perp strain $\approx 0.011$, but underestimated in this fit.

After longer equilibration:

||||
|:-:|:-:|:-:|

Perp strain $\approx 0.02$

The linear regime only comes after a rapid increase for short distances in $E^\parallel$. I believe it comes from the fact that a few edges must be followed in parallel space before the corresponding trajectory "folds back" in perp space. I expect the height of the plateau to be around the size of the acceptance region of the quasicrystal, ie. the width of the dense cloud of points in perp space for our lifted tilings.

#### A point of comparison

To get an idea of the magnitude of the perpendicular strains, I computed the perpendicular strain of a periodic array of octagons, which might play a role analogous to the sigma phase for the square triangle tiling.


This confirms that our tilings are indeed of rather poor quality.

Next:
* Repeat the measurement on other tilings, see if, eg. having a free boundary with a fluid helps.
* Improve fitting bounds.

For the sigma phase:


$$
v_x^\parallel = e_1^\parallel + 2 e_2^\parallel - e_4^\parallel = (1 + \sqrt{3}; 0)\\
v_y^\parallel = -e_1^\parallel + 2 e_3^\parallel + e_4^\parallel = (0; 1 + \sqrt{3})\\
v_x^\perp = e_1^\perp + 2 e_2^\perp - e_4^\perp = (1 + \sqrt{3}; 0)\\
v_y^\perp = -e_1^\perp + 2 e_3^\perp + e_4^\perp = (0; 1 + \sqrt{3})\\
$$

$$
A = (2 - \sqrt{3})
\begin{pmatrix}
-1 & 0 \\
0 & 1
\end{pmatrix}
$$

$$
\xi = 2\sqrt{2} - \sqrt{6} \approx 0.379
$$

### Searching for a coexistence

We look for state points at which a QC cluster form in the fluid, and does not span the box (full free boundary) to see if that improves the perpendicular strain and annealing of defects.

Interpolating between the simulations we already have, at $q=0.55$, it seems that the sweet is given by the following line (note that the x axis is $x_L$ and not the usual $x_S$ !).


At $q = 0.5$ the interfacial tension between QC and fluid seems even smaller and we often obtain dendritic tiling regions rather than dense clusters. Moreover, the S1 squares seem much more favoured and S1 clusters are commonly observed and take over quickly as soon as we approach $x = 0.5$.

[05/11/2022]

We perform the tiling analysis over time for two systems at $q = 0.55$ and $x_L = 0.325$. The first one has packing fraction $\eta = 0.835$ and shows typically an island of tiling in coexistence with a fluid. The second one has packing fraction $\eta = 0.85$ and forms a system-spanning tiling.

* $\eta = 0.835$

||||
|:-:|:-:|:-:|

||||
|:-:|:-:|:-:|
|Frame 10|Frame 50|Frame 100|

* $\eta = 0.85$

||||
|:-:|:-:|:-:|

||||
|:-:|:-:|:-:|
|Frame 10|Frame 50|Frame 100|

It is clear that, while the tiling is formed very quicly at the lowest packing fraction, is is still forming in the second case at the end of the simulation. In both cases, the perpendicular strain is around 1.2, only about half the "first approximant" one, so it could correspond to a periodic phase with only slightly larger unit cell. Moreover, red and orange small squares do not seem to be evenly distributed in the tilings. This makes me doubt the quasicrystalline nature of the self-assembled phase, which could instead be highly defective periodic structures, twinned in two possible orientations...

## QC12 analysis

We ran self-assembly simulations at $q = 0.45$ and $q = 0.5$ for $x_S \in [0.3, 0.4]$ and $\eta \in [0.82, 0.86], in the region where we expect QC12 to form.

Several system exhibit a 2-fold symmetric diffraction pattern. It seems that size ratio $q=0.45$ yields higher quality structures.