# HMM(Hidden Markov Model)

參考資料:

[pansci](http://pansci.asia/archives/43586)

[wiki hmm](https://zh.wikipedia.org/wiki/%E9%9A%90%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E6%A8%A1%E5%9E%8B)

[youtube](https://hackmd.io/IwDghiDGwMwGwFoAmAmAnAIwQFgAweARG0gFYEUB2YAMzDjjDSUpCA==)

---
### 歷史:
- DNN 出現之前重要的 ML model (1980s~2000s)
### 用於:
- 基因解碼
- 語音辨識
- 股價預測
- etc

---

原理:

x — 隱含狀態
y — 可觀察的輸出
a — 轉換機率（transition probabilities）
b — 輸出機率（output probabilities）

若滿足Markov property:${\mathbb {P}}(X_{n}=x_{n}|X_{{n-1}}=x_{{n-1}},\dots ,X_{0}=x_{0})={\mathbb {P}}(X_{n}=x_{n}|X_{{n-1}}=x_{{n-1}}).$
模型複雜度:O(NM^2)
N - observed state 數量
M - hidden state 數量

$Y=y(0),y(1),...,y(L-1)$ observed variable sequence
$X=x(0),x(1),...,x(L-1)$ hidden variable sequence
$P(Y)=\sum_{X}P(Y\mid X)P(X)\,)$ model, sequence長度為 ${\displaystyle L}$

---
## 三個典型問題

- 預測
${\displaystyle P(x(t)\ |\ y(1),\dots ,y(t))}$ use forward algorithm
- 平滑化
${\displaystyle P(x(k)\ |\ y(1),\dots ,y(t)),k<t}$ use forward-backward algorithm

- 解碼
${\displaystyle P([x(1)\dots x(t)]|[y(1)\dots ,y(t)])\,}$ use Viterbi algorithm

- 統計語意分析
-
---

## Viterbi ALgorithm

假設給定隱式馬可夫模型（HMM）狀態空間 ${\displaystyle S}$，共有$k$個狀態，初始狀態 ${\displaystyle i}$ 的機率為 ${\displaystyle \pi _{i}}$ ，從狀態 ${\displaystyle i}$到狀態${\displaystyle j}$ 的轉移機率為 ${\displaystyle a_{i,j}}$。 令觀察到的輸出為 ${\displaystyle y_{1},\dots ,y_{T}}$。 產生觀察結果的最有可能的狀態序列 ${\displaystyle x_{1},\dots ,x_{T}}$由遞迴關係給出：

$\begin{array}{rcl}V_{1,k}&=&\mathrm {P} {\big (}y_{1}\ |\ k{\big )}\cdot \pi _{k}\\V_{t,k}&=&\mathrm {P} {\big (}y_{t}\ |\ k{\big )}\cdot \max _{x\in S}\left(a_{x,k}\cdot V_{t-1,x}\right)\end{array}$

此處 ${\displaystyle V_{t,k}}$ 是前 ${\displaystyle t}$ 個最終狀態為 ${\displaystyle k}$的觀測結果最有可能對應的狀態序列的機率。 通過儲存向後指標記住在第二個等式中用到的狀態 ${\displaystyle x}$ 可以獲得維特比路徑。聲明一個函式 ${\displaystyle \mathrm {Ptr} (k,t)}$ ，它返回若 ${\displaystyle t>1}$時計算 ${\displaystyle V_{t,k}}$用到的${\displaystyle x}$值 或若 ${\displaystyle t=1}$時的 ${\displaystyle k}$. 這樣:

$\begin{array}{rcl}x_{T}&=&\arg \max _{x\in S}(V_{T,x})\\x_{t-1}&=&\mathrm {Ptr} (x_{t},t)\end{array}$
這裡我們使用了$arg max$的標準定義 演算法複雜度為 $O(T\times \left|{S}\right|^{2})$

---
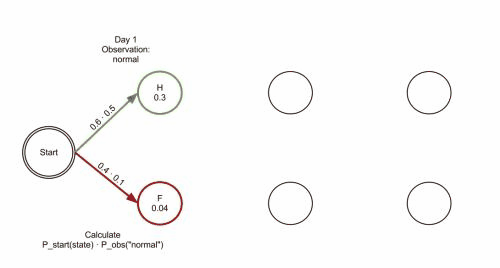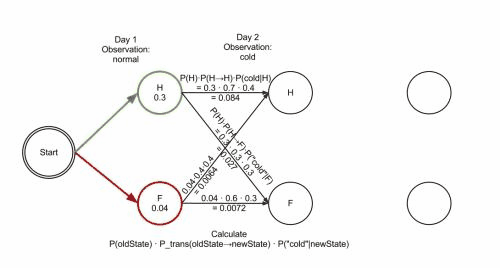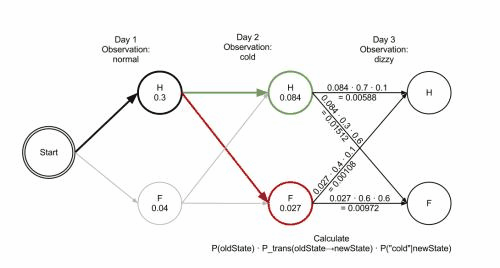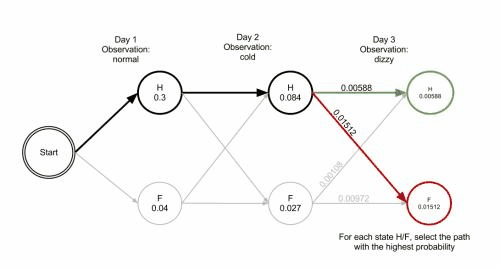
## Example

states = ('Healthy', 'Fever')
 
observations = ('normal', 'cold', 'dizzy')
 
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
 
transition_probability = {
   'Healthy' : {'Healthy': 0.7, 'Fever': 0.3},
   'Fever' : {'Healthy': 0.4, 'Fever': 0.6},
   }
 
emission_probability = {
   'Healthy' : {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
   'Fever' : {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6},
   }

用狀態機表示:

# Helps visualize the steps of Viterbi.
def print_dptable(V):
    print "    ",
    for i in range(len(V)): print "%7d" % i,
    print

    for y in V[0].keys():
        print "%.5s: " % y,
        for t in range(len(V)):
            print "%.7s" % ("%f" % V[t][y]),
        print

def viterbi(obs, states, start_p, trans_p, emit_p):
    V = [{}]
    path = {}

    # Initialize base cases (t == 0)
    for y in states:
        V[0][y] = start_p[y] * emit_p[y][obs[0]]
        path[y] = [y]

    # Run Viterbi for t > 0
    for t in range(1,len(obs)):
        V.append({})
        newpath = {}

        for y in states:
            (prob, state) = max([(V[t-1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
            V[t][y] = prob
            newpath[y] = path[state] + [y]

        # Don't need to remember the old paths
        path = newpath

    print_dptable(V)
    (prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
    return (prob, path[state])

def example():
    return viterbi(observations,
                   states,
                   start_probability,
                   transition_probability,
                   emission_probability)
print example()


---

## Baidu Jieba