# 什麼是轉置矩陣（Transposed Convolution）
###### tags: `AI面試精選題`

## 目錄
* Convolution 簡介
* Transposed Convolution 簡介
* 實際案例

## 卷積（Convolution）簡介
- Convolution 是一個「將原始資料縮透過遮罩（Mask）縮減成少量關鍵特徵」的技術，用數學角度想就是將原始資料與 Mask 進行「線性轉換」。
- 圖像辨識：透過 Convolution 將原始圖片搭配 Mask 運算後，得出有用的特徵圖（Feature Map）。
- Output Size = $1 + \frac{size\ of\ image\ – kernel\ size\ + 2*padding}{stride}$
- 訊號處理：透過 1D Convolution 將原始訊號轉換成「特徵訊號」。

## Transposed Convolution 簡介
- 剛好跟 Convolution 的功能「完全相反」。
- 將某個 Pixel 或資料點以「線性轉換」方式轉換成多個資料

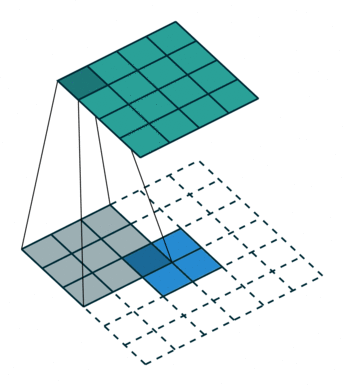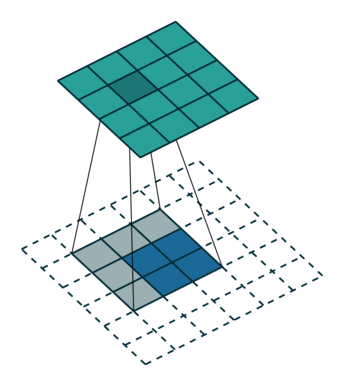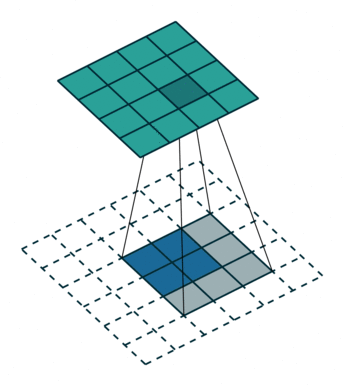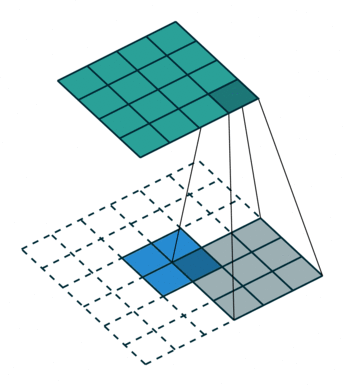
## 用數學方式理解 Convolution、Transpose Convolution 的運作
- 已知有一張 4*4 的 Image、一張 3*3 的 Kernel，以及透過 Kernel 將 Image 線性轉換後的 Output，Image 中每個 Pixel 為 $I=\{I_{ij} | i = 1, 2, 3, 4; j = 1, 2, 3, 4\}$，Kernel 中每個 Pixel 為 $K=\{K_{ij} | i = 1, 2, 3; j = 1, 2, 3\}$，Output 中每個 Pixel 為 $O=\{O_{ij} | i = 1, 2; j = 1, 2\}$。
$$
O_{11}=I_{11}K_{11}+I_{12}K_{12}+I_{13}K_{13}+I_{21}K_{21}+I_{22}K_{22}+I_{23}K_{23}+I_{31}K_{31}+I_{32}K_{32}+I_{33}K_{33} \\
O_{12}= I_{12}K_{11}+I_{13}K_{12}+I_{14}K_{13}+I_{22}K_{21}+I_{23}K_{22}+I_{24}K_{23}+I_{32}K_{31}+I_{33}K_{32}+I_{34}K_{33}\\
O_{21}= I_{21}K_{11}+I_{22}K_{12}+I_{23}K_{13}+I_{31}K_{21}+I_{32}K_{22}+I_{33}K_{23}+I_{41}K_{31}+I_{42}K_{32}+I_{43}K_{33}\\
O_{22}= I_{22}K_{11}+I_{23}K_{12}+I_{24}K_{13}+I_{32}K_{21}+I_{33}K_{22}+I_{34}K_{23}+I_{42}K_{31}+I_{43}K_{32}+I_{44}K_{33}\\
$$
- 若將 Convolution 以 Matrix Multiplication 計算，則：
$$
I= \begin{bmatrix}
I_{11} \\
I_{12} \\
I_{13} \\
I_{14} \\
I_{21} \\
I_{22} \\
I_{23} \\
I_{24} \\
I_{31} \\
I_{32} \\
I_{33} \\
I_{34} \\
I_{41} \\
I_{42} \\
I_{43} \\
I_{44}
\end{bmatrix}_{1*16}
\\
K= \begin{bmatrix}
K_{11} & K_{12} & K_{13} & 0 & K_{21} & K_{22} & K_{23} & 0 & K_{31} & K_{32} & K_{33} & 0 & 0 & 0 & 0 & 0 \\
0 & K_{11} & K_{12} & K_{13} & 0 & K_{21} & K_{22} & K_{23} & 0 & K_{31} & K_{32} & K_{33} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & K_{11} & K_{12} & K_{13} & 0 & K_{21} & K_{22} & K_{23} & 0 & K_{31} & K_{32} & K_{33} & 0 \\
0 & 0 & 0 & 0 & 0 & K_{11} & K_{12} & K_{13} & 0 & K_{21} & K_{22} & K_{23} & 0 & K_{31} & K_{32} & K_{33}
\end{bmatrix}_{4*16}
\\
O= K_{4*16} \cdot I_{16*1}=\begin{bmatrix}
O_{11} \\
O_{12} \\
O_{21} \\
O_{22} \\
\end{bmatrix} \\
$$
- Transposed Convolution 就是從轉成矩陣的 Convolution 進行轉換的

$$
K^{T}=\begin{bmatrix}
K_{11} & 0 & 0 & 0 \\
K_{12} & K_{11} & 0 & 0 \\
K_{13} & K_{12} & 0 & 0 \\
0 & K_{13} & 0 & 0 \\
K_{21} & 0 & K_{11} & 0 \\
K_{22} & K_{21} & K_{12} & K_{11} \\
K_{23} & K_{22} & K_{13} & K_{12} \\
0 & K_{23} & 0 & K_{13} \\
K_{31} & 0 & K_{21} & 0 \\
K_{32} & K_{31} & K_{22} & K_{21} \\
K_{33} & K_{32} & K_{23} & K_{22} \\
0 & K_{33} & 0 & K_{23} \\
0 & 0 & K_{31} & 0 \\
0 & 0 & K_{32} & K_{31} \\
0 & 0 & K_{33} & K_{32} \\
0 & 0 & 0 & K_{33}
\end{bmatrix}_{4*16}
O=\begin{bmatrix}
O_{11} \\
O_{12} \\
O_{21} \\
O_{22}
\end{bmatrix}_{1*4}
I= O_{1*4}\cdot K_{4*16} \\
$$

## 實際案例
### Generative Adversarial Network
- 一種影像生成的深度學習演算法
- Discriminator Network：判斷生成出來的圖片與真實圖片是否相同或相似。
- Generator Network：藉由 D-dimensional noise vector 產生出一張偽圖片，其中就會大量使用到 Transposed Convolution。

### U-Net
- 影像切割案例中最常使用的深度學習架構
- 在 Encoder 階段，將圖片以 CNN 方式萃取出關鍵特徵
- 在 Decoder 階段，除了以 Transposed Convolution 將 Feature Map 中每個特徵轉換成多個特徵外，部分 Encoder 階段得到的 Feature Map 也會在此階段搭配運算。

### Reference
Mozaffari M.H. and Tay L.L. (2020). A Review of 1D Convolutional Neural Networks toward Unknown Substance Identification in Portable Raman Spectrometer. *arXiv:2006.10575*