# 演算法作業六
## 觀念題
### 第1題: Huffman Code
:::info
###### 說明
- 已知一份文件內7個符號出現的頻率為:
- A:2, B:8: C:3, D:4, E:6, F:10, G:7
:::
1. 請找出此7個符號的Huffman code
1. 首先要先畫出賀夫曼tree
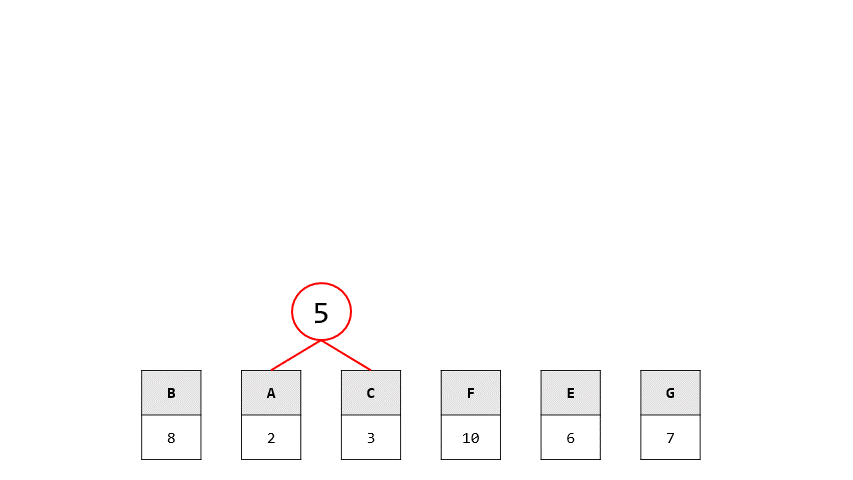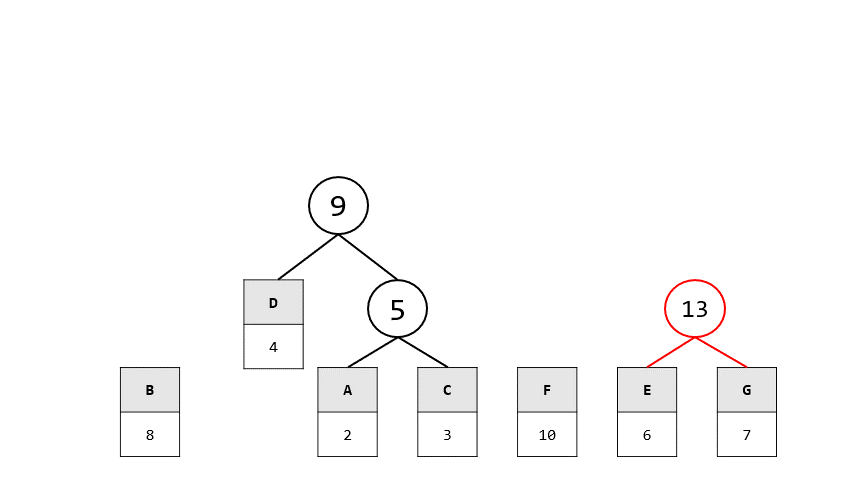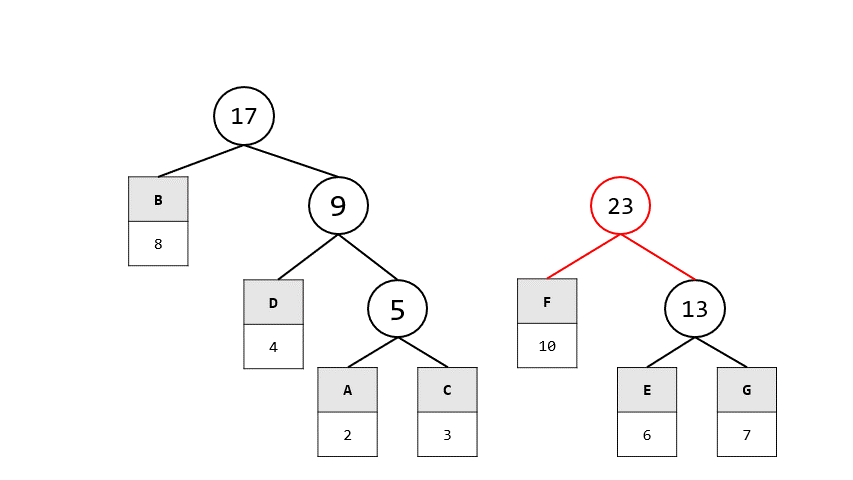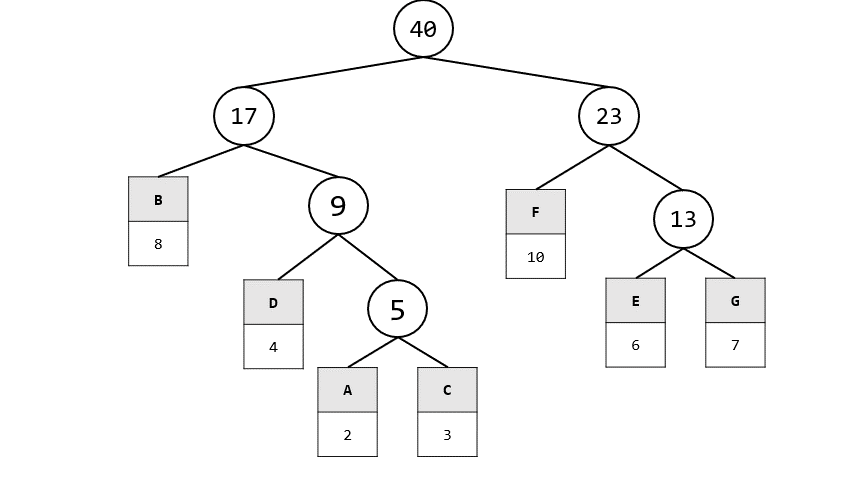
2. 再來找出全部的編碼即可
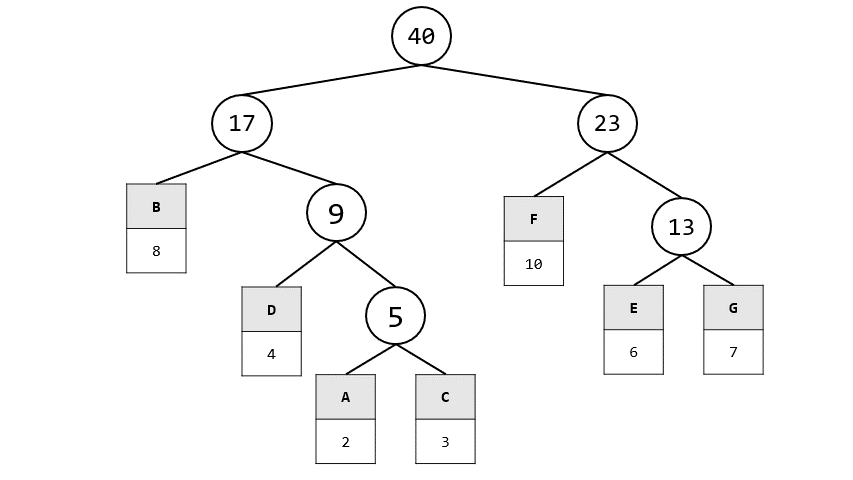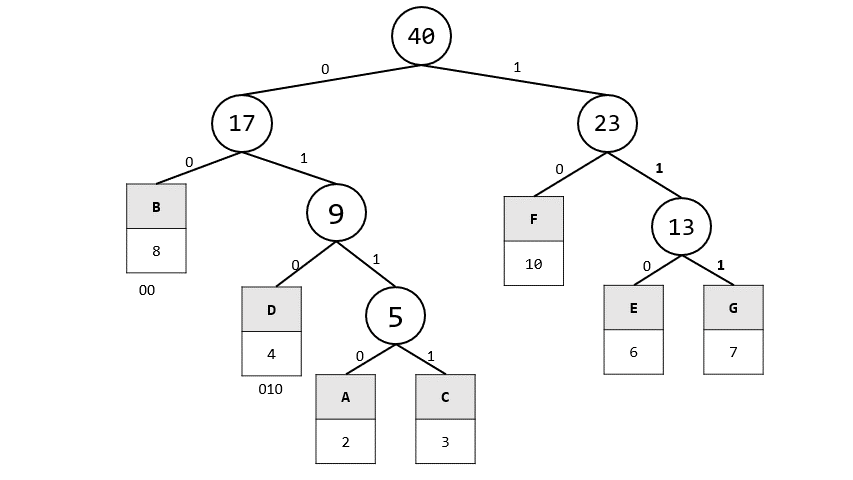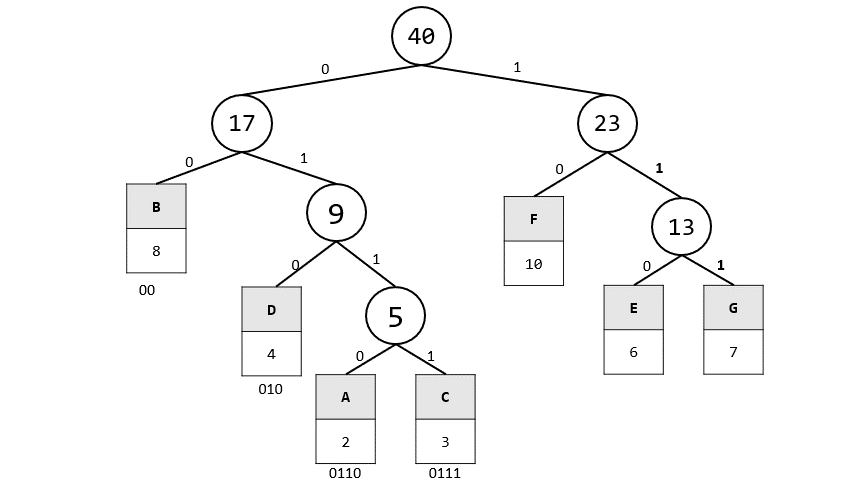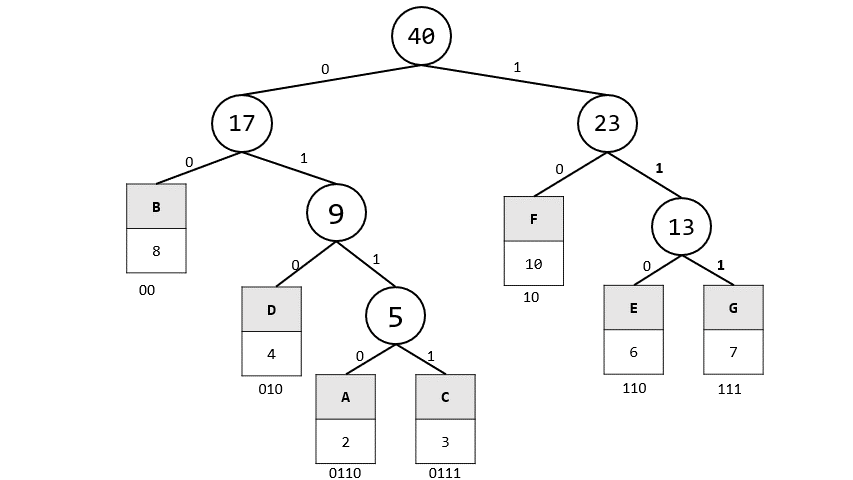
3. 答案
```
A: 0110
B: 00
C: 0111
D: 010
E: 110
F: 10
G: 111
```
2. 若有一組編碼為1100110111,求解碼後的符號

> EAG
### 第2題: 換錢問題
:::info
###### 說明
- 新台幣常用的紙鈔、硬幣有1元,5元,10元,50元,100元,500元,1000元
- 若要提領n元,如何以最少數量的紙鈔、硬幣組成 n 元
- 請以Greedy策略設計出一個演算法解決換錢問題,並以說明此演算法符合Greedy的3個條件
:::
- 首先先用1000元盡量貼近n元
- 再來盡量用500元貼近$n-1000*A_1000$
- 以此類推
- 以1699為例
- 首先用1張一千,此時剩下699
- 再來用1張五百,此時剩下199
- 接著用1張一百,此時剩下99
- 再者用1個五十元,此時剩下49
- 然後用4個十元,此時剩下9
- 然後用1個五元,此時剩下4
- 最後用4個一元,結束找零
- 在這裡此演算法有滿足貪心三大特性
- Sloved by a sequence of decision
- 在找零問題中有1000,500,100,50,10,1
- 因此階段明確
- Each decision is locally optimal
- 在問題中,每一階段都有最大值
- 因此滿足在該階段最佳
- Finally add up to globally optimal solution
- 因為各零錢都是整數被關係,因此不互相引響
- PS: 如果不是要用DP
- 因此滿足最終結果最佳化
### 第3題: Dijkstra演算法
:::info
###### 說明
- 請用Dijkstra演算法找出下圖的由a出發的shortest path tree,並完成右表。

:::
- 答案
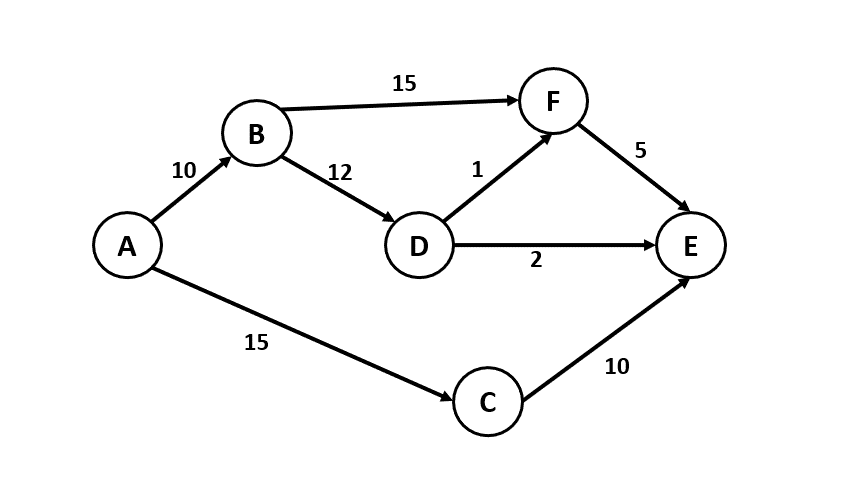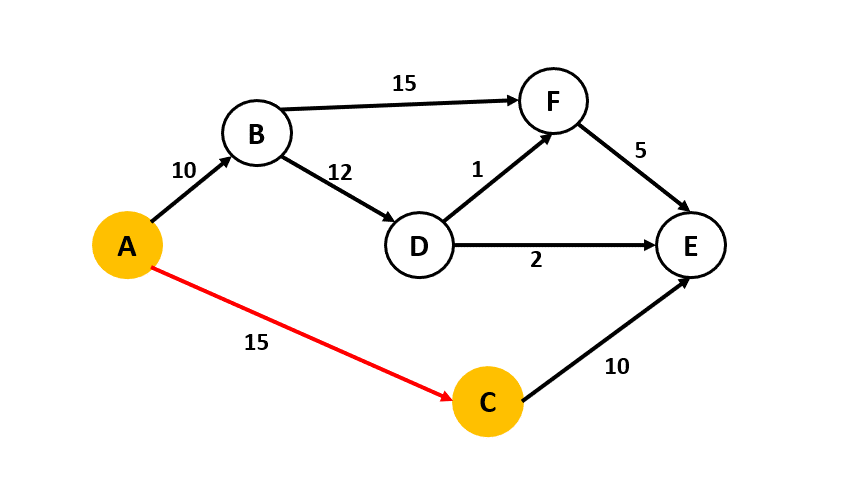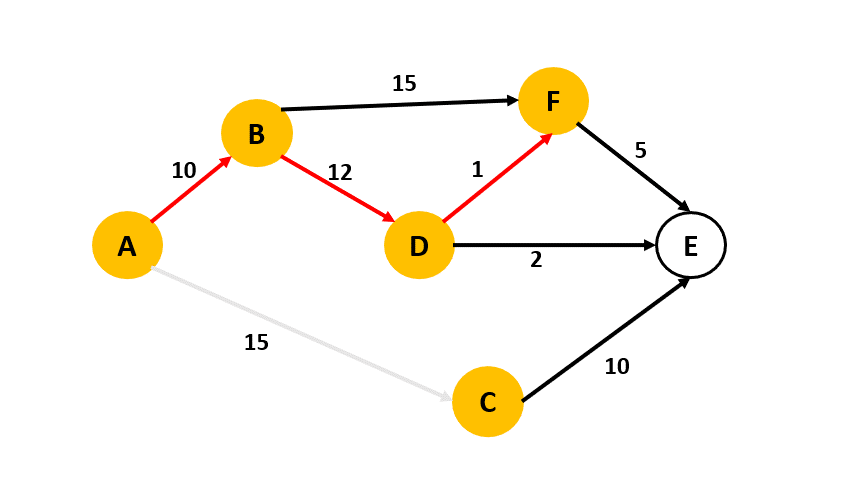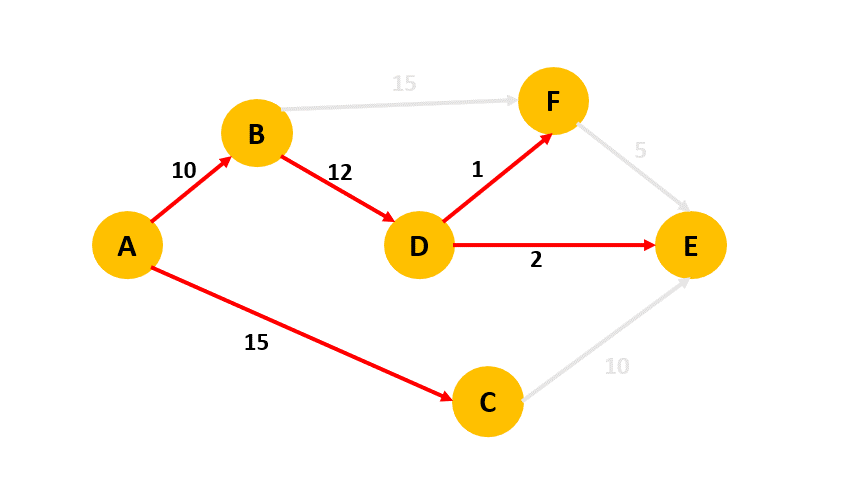
|round|vertex|B|C|D|E|F|
|:----|:----|:----|:----|:----|:----|:----|
|1|B|10|15|$\infty$|$\infty$|$\infty$|
|2|C|10|15|22|$\infty$|25|
|3|D|10|15|22|25|25|
|4|F|10|15|22|24|23|
|5|E|10|15|22|24|23|
## 程式題
### 第4題:隔出最多的水
[leetcode 11](https://leetcode.com/problems/container-with-most-water/)
- 程式碼
:::spoiler rust
```rust=
use std::cmp;
impl Solution {
pub fn max_area(height: Vec<i32>) -> i32 {
let mut left = 0;
let mut right = height.len()-1;
let mut maximum = 0;
while left<right{
let area = cmp::min(height[left],height[right]) * (right-left) as i32;
maximum = cmp::max(maximum,area);
if height[left]<height[right]{
left += 1;
}
else if height[left]>height[right]{
right -= 1;
}
else{
left += 1;
right -= 1
}
}
assert!(left>=right);
maximum
}
}
```
:::
- 執行結果

- 花費時間: 15分鐘
- 完成程度: 有看別人的程式碼
- [ref1](https://clay-atlas.com/blog/2021/01/15/leetcode-11-container-with-most-water-%E8%A7%A3%E9%A1%8C%E7%B4%80%E9%8C%84/)
- 思路
:::info
###### 須知
$area = min(height[left],height[right])*(rigjt-left)$
:::
原來是雙指針+貪心
- 將指針指向頭尾
- 然後計算面積大小 => 並和最大面積進行比較and替換(如果更大)
- 然後可以貪心了
- 我們貪的是該指針指向的高度要大
- 如果較小的就繼續往前搜尋
### 第5題:跳到最後-V2
[leetcode 45](https://leetcode.com/problems/jump-game-ii/)
- 程式碼
:::spoiler rust
```rust=
use std::cmp;
impl Solution {
pub fn jump(nums: Vec<i32>) -> i32 {
let mut jump = 0;
let mut left:i32 = 0;
let mut right:i32 = 0;
for i in 0..nums.len()-1 {
right = cmp::max(right,i as i32+nums[i] );
if i as i32 == left{
jump += 1;
left = right ;
}
}
jump
}
}
```
:::
- 執行結果

- 花費時間: 30分鐘
- 完成程度: 本來有自己想,但後來被測資搞到,就有看別人的作法
- [ref1](https://leetcode.com/problems/jump-game-ii/solutions/4899413/greedy-python)
- 思路
- 大前提: 這題保證可以抵達最後(我剛開始沒看到,被弄很久)
- 因為可以抵達最後,所以我們就直接不當成充電問題了(上周我把這題當成充電站看)
- 那我們一樣可以用雙指針來思考
- left代表上一次跳的最大距離
- right代表從[0,i]可跳的最大距離
- 接下來就是模擬了
- 當我們抵達left的地方時就可以視為跳了一次
- `jump++`
- 並`left = right`
- 然後right每次都會去計算哪個點可以跳最遠
### 第6題:2個城市的面試排程
[leetcode 1029](https://leetcode.com/problems/two-city-scheduling/)
- 程式碼
:::spoiler rust
```rust=
impl Solution {
pub fn two_city_sched_cost(mut costs: Vec<Vec<i32>>) -> i32 {
costs.sort_by_key(|row| row[0] - row[1]);
let mut totalCost = 0;
for i in 0..costs.len()/2{
totalCost += costs[i][0];
}
for i in costs.len()/2..costs.len(){
totalCost += costs[i][1];
}
totalCost
}
}
```
:::
- 執行結果

- 花費時間: 15分鐘
- 完成程度: 完全靠自己
- 思路
- 首先我們要先排序過一次車票價格
- 排序的規則是$city1-city2$,降序
- 然後排序完成後,因為數值越小代表city1越便宜,數值越達代表city2越便宜,因此
- 前n/2個就可以去city1
- 後n/2個就可以去city2
## 心得
這周可以放春假,下周要期中考,上機考使我心慌慌。
這周學了更多的貪心,令我沒想到的是計概學到的Huffman code居然是貪心,真是太意外了,但後來想想其實蠻合理的,因為每一步都是找最小。BTW,2-terminal one to any special channel routung problem,讓我回想起數位邏輯實習標準佈線的可怕回憶(線線不能重疊)
然後作業的部分,我比較有印象的是跳到最後2,我本來想的超複雜,還想說還要判斷能不能跳到最後,結果不用(徐聖凱下次請看清楚題目好嗎),anyway,後來還看別人的扣,才發現不用判斷討厭,反正我下次真的要看清楚題目:(。
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet