# 演算法作業 HW5

## 觀念題
### 第1題: Heap Sort
1. 下圖為Max Heap。Heap Sort的每一回合，會將Heap的最大值刪除後，又恢復為Heap。請畫出第一回合恢復的過程。
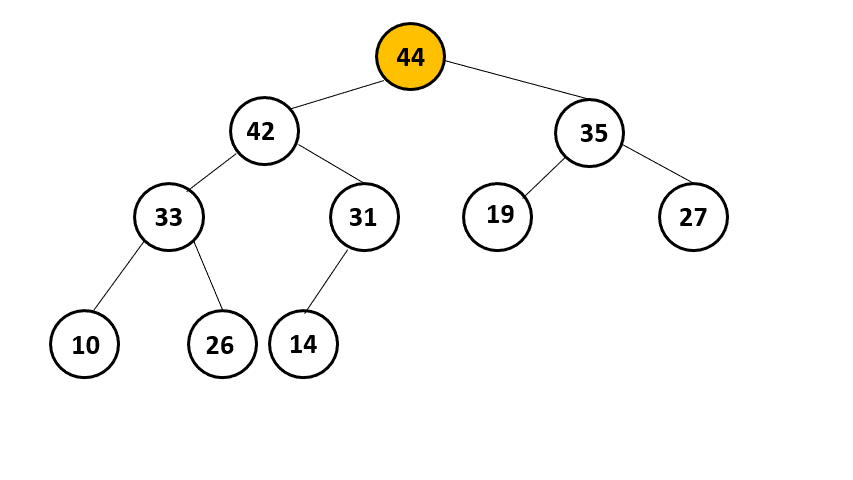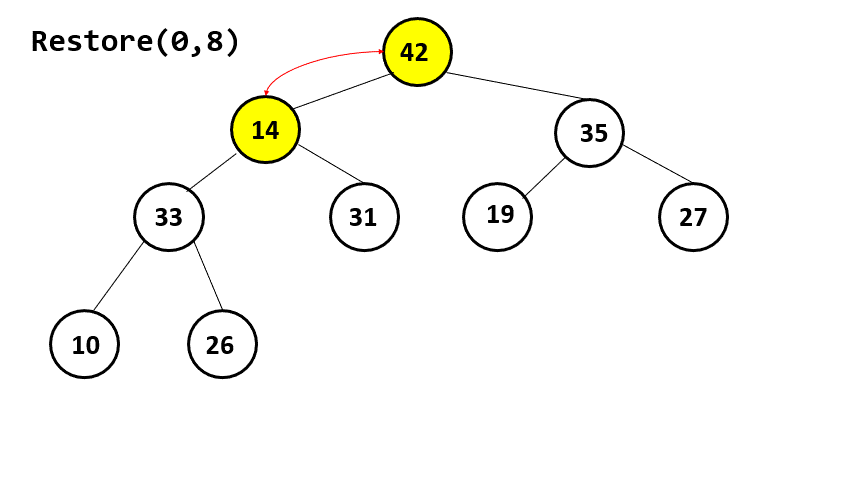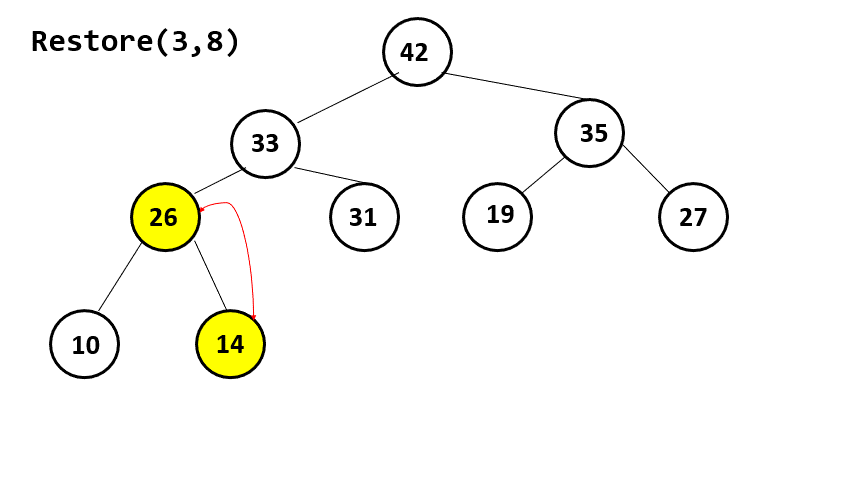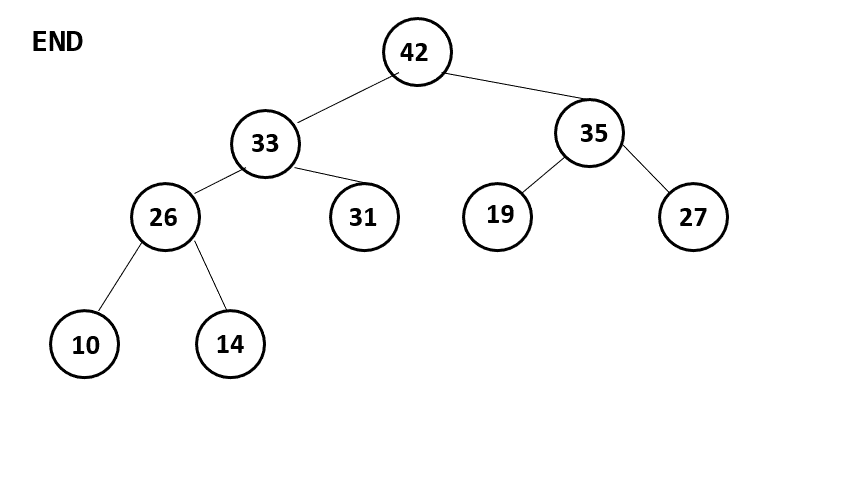
2. 投影片69頁的公式如下，請解釋此公式的含意。
- 首先，假設樹高為d，並令L為當前層數

- 然後，我們就可以知道
- L層時總共有$2^L$個節點
- 1個節點最糟要比較$2(d-L)$(一個節點最多兩個小孩)
- 最後我們只要將$\Sigma step*number$即可
- 公式整理

### 第2題: Problem平均的Lower Bound
- 下圖為二元樹。參考投影片77頁，請算出二元樹的External Path Length，以及葉子平均深度。
- **External Path Length：** $3*4 + 2*2= 16$
- **葉子平均深度：** $16/6 = 2.67$

### 第3題: Problem Transformation
- Sorting problem reduces to Convex Hull Problem
- 請說明，若要排序五個數字：4,1,3,2,5，如何轉為Convex Hull Problem後，完成排序。
:::info
1. 五個數列$<4,1,3,2,5>$
2. 先做transformation，做成$(x,x^2)$形式
- $<(4,16),(1,1),(3.9),(2,4),(5,25)>$
3. 接下來使用Convex Hull解決此問題，可得
- $<(1,1),(2,4),(3.9),(4,16),(5,25)>$
4. 在做transformation，做成$x$形式
- $<1,2,3,4,5>$
:::
- 因此，我們可以發現Sorting problem reduces to Convex Hull Problem
- 且Convex Hull Problem比較難解決
- 因此$\Omega(convex) >= \Omega(sort)-\Omega(\alpha)$
- 因此我們可以說Convex Hull Problem之lower bound是$O(nlogn)$

## 程式題

### 第4題：圓型打字機
- 程式碼
:::spoiler rust

    impl Solution {
        pub fn min_time_to_type(word: String) -> i32 {
            let mut currentChr = b'a';
            let mut step = 0;
            for i in word.bytes(){
                let clockwise = i32::abs(i as i32 - currentChr as i32);
                step += std::cmp::min(clockwise, 26-clockwise) + 1;
                currentChr = i;
            }
            step
        }
    }

:::
- 執行結果
- 花費時間：10分鐘
- 完成程度：靠自己
- 思路
1. 這題直接用模擬就好(模擬打字機)
2. 每一輪打字時去一直找最小值($min(順時鐘,逆時鐘)$)，並且找完後要切換字元
3. 然後然後，因為打字也要時間，所以每一輪記得+1

### 第5題：跳到最後
- 程式碼
:::spoiler rust

    impl Solution {
        pub fn can_jump(nums: Vec<i32>) -> bool {
            if nums.len() == 1{
                return true;
            }

            let mut step = nums[0];
            for i in 0..nums.len(){
                if (step <= 0){
                    return false;
                }
                step -= 1;
                println!("{}",step);
                if nums[i] > step{
                    step = nums[i];
                }

            }
            return true;
        }
    }

:::
- 執行結果
- 花費時間：20分鐘
- 完成程度：參考網路解法
- [ref 1](https://leetcode.com/problems/jump-game/solutions/4534808/super-simple-intuitive-8-line-python-solution-beats-99-92-of-users/)
- 思路
~~其實看到別人解題方式覺得這題好好玩~~
1. **大前提：** 只要當前可走步數=0，就代表跟本不可能
2. ~~那我們可以把這題當成gogoro換電站~~
- 當下電池：我目前最多可以跳幾步
- 換電站電量：每一節點提供你可以跳的步數
3. 所以每一輪的行為是
- 先判斷：我現在步數>0，如果不是則不可能
- 步數-1
- 最後去判斷，當前步數跟充電站的電量是否達到可交換的程度，是就交換

### 第6題：由各行的和與各列的和求矩陣
- 程式碼
:::spoiler rust

    impl Solution {
        pub fn restore_matrix(row_sum: Vec<i32>, col_sum: Vec<i32>) -> Vec<Vec<i32>> {
            let rowSize = row_sum.len();
            let colSize = col_sum.len();

            let mut row_sum = row_sum;
            let mut col_sum = col_sum;

            let mut ans = vec![
                vec![0;colSize]
            ;rowSize];

            let mut i = 0;
            let mut j = 0;

            while i<rowSize && j<colSize{
                ans[i][j] = std::cmp::min(row_sum[i],col_sum[j]);
                row_sum[i] -= ans[i][j];
                col_sum[j] -= ans[i][j];

                if row_sum[i] == 0{
                    i += 1;
                }
                if col_sum[j] == 0{
                    j += 1;
                }
            }
            ans
        }
    }

:::
- 執行結果
- 花費時間：30分鐘
- 完成程度：參考網路解法
- [ref1](https://leetcode.com/problems/find-valid-matrix-given-row-and-column-sums/solutions/1572656/easy-python-solution-o-n-m-t-beats-100-explanation/)
- 思路
~~這題看到別人思路有一瞬間覺得自己超笨~~
0. 其實這題有點像2D版雙指針
1. **大前提：** 我們從<0,0>開始推演就好了
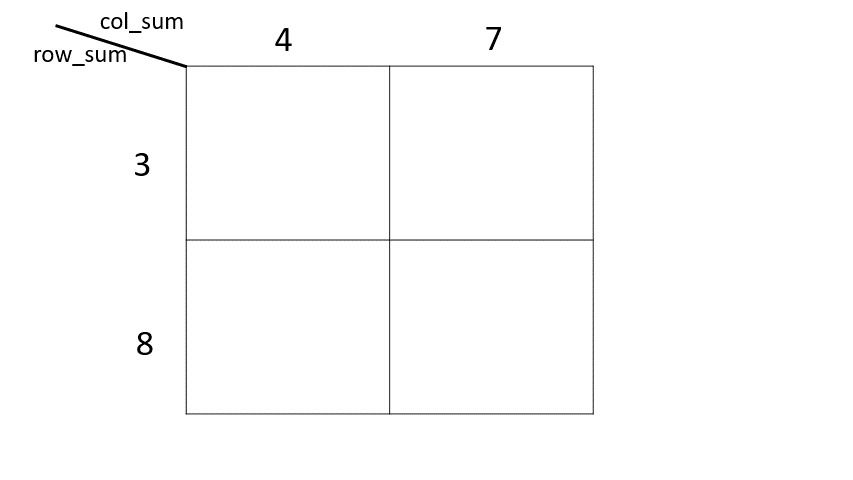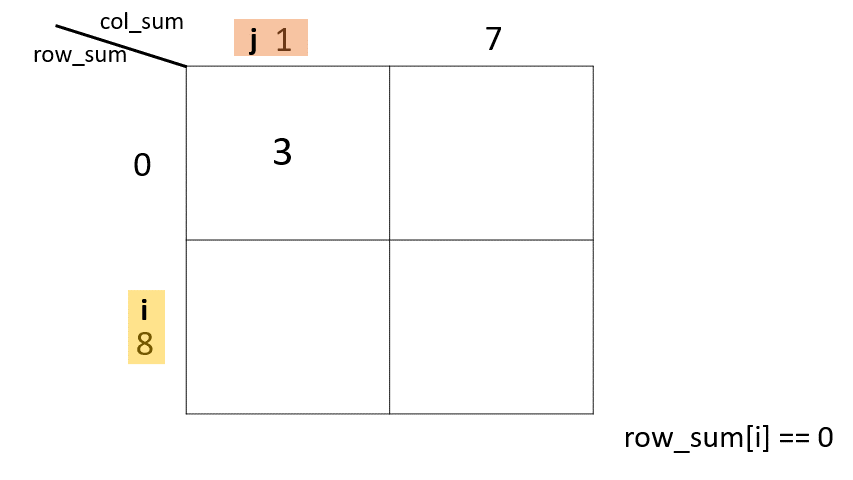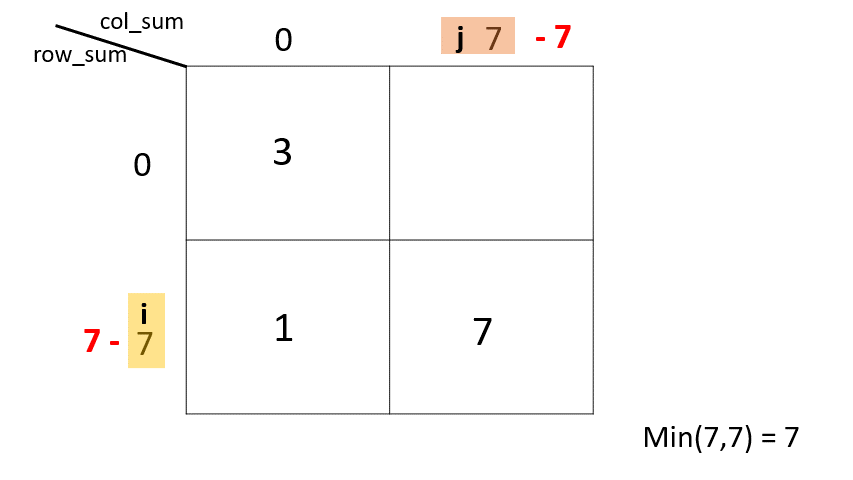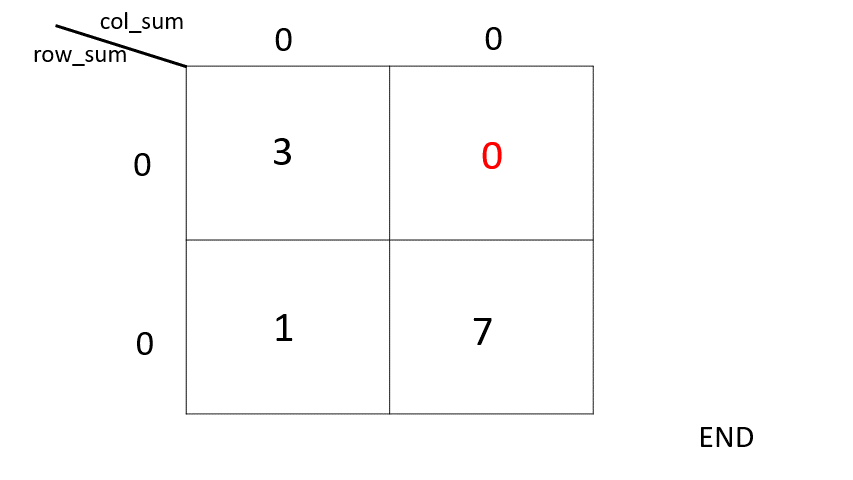
2. 當進入A<i,j>時我們做三件事
1. $min(row[i],col[j])$
2. 將row[i]與col[j]分別減去剛剛取的min
- 為什麼要找最小，因為有減去的動作，以做到避免負數
3. 最後去看row[i]或col[j]是否為零，如果是就i++orj++
ps. 剩下沒用到的要補0喔
3. 以測試資料1舉例

## 心得
好快樂，作業直接開放兩周我覺得是非常好的政策，我覺得使我在時間的運用上更有彈性。

這周主要學了貪心，以及提升lower Bound的方法，我印象最深的是Dijksstra演算法(畢竟計算機網路IP層要算這個，然後我去問陳家銓同學他居然回我以為你學過了:( )，我今天上完才發現原來他也用到了貪心的概念，感覺好酷。

貪心法感覺平常寫程式就一直有在用，我以為我這周作業能速速解決，事實證明我太天真了，看來我還需要提升貪心的技巧。