# 演算法第14周
:::info
**最後的作業,希望演算法不要明年再來**
:::
## 觀念題
### 第1題: leetcode 300 延伸
[leetcode 300](https://leetcode.com/problems/longest-increasing-subsequence/)
- 程式碼
:::spoiler C++
```C++=
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int size = nums.size();
vector<int> dp(size,1);
for (int i=0; i<size; i++){
for (int j=0; j<i; j++){
if (nums[i]>nums[j]){
dp[i] = max(dp[i],dp[j] + 1);
}
}
}
int res = 0;
for_each(dp.begin(),dp.end(), [&](const auto & num){res = max(res,num);});
return res;
}
};
```
:::
- 執行結果

- 解法
- 讓$dp[i]$表示從$1-i$遞增的數列長度
- 則轉移式就是$dp[i] = max(dp[j]+1)$ $\forall j \in [0,n)$
- 圖解
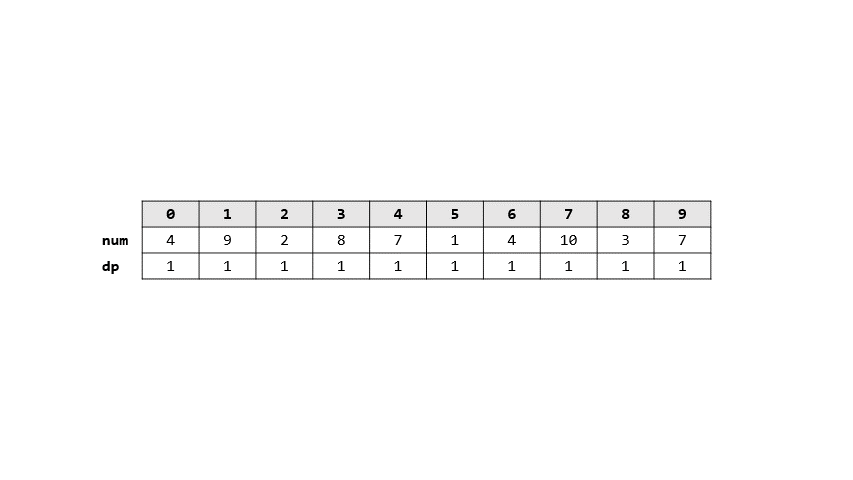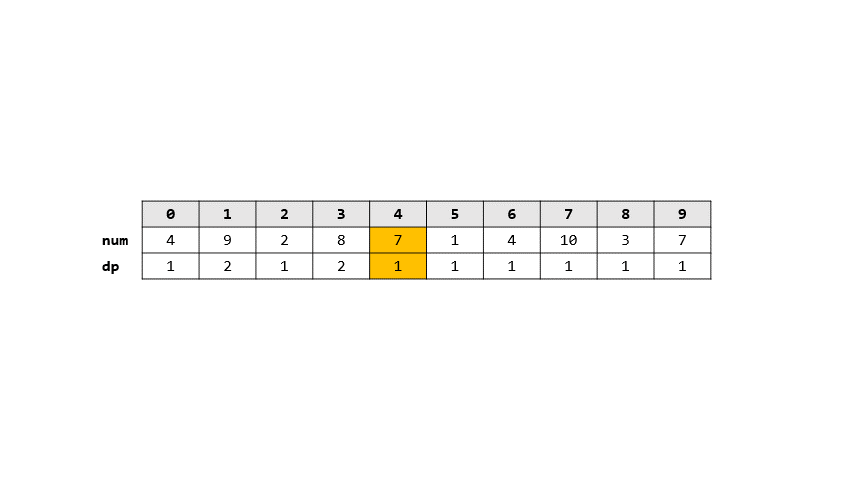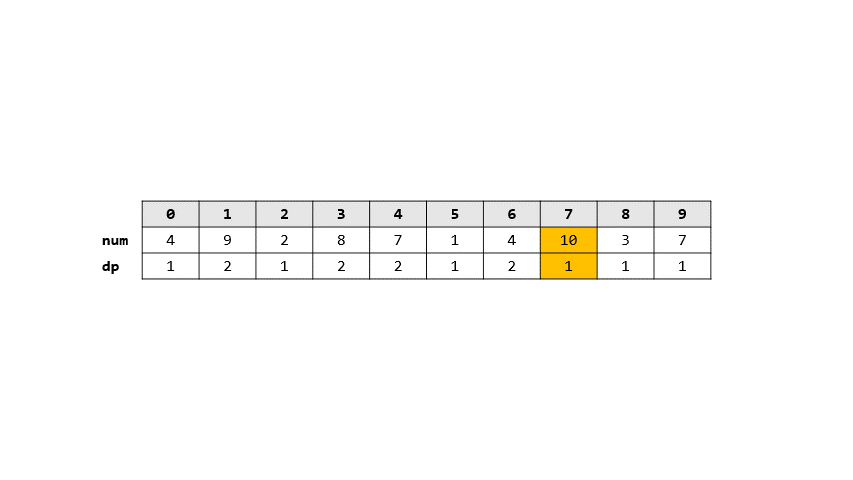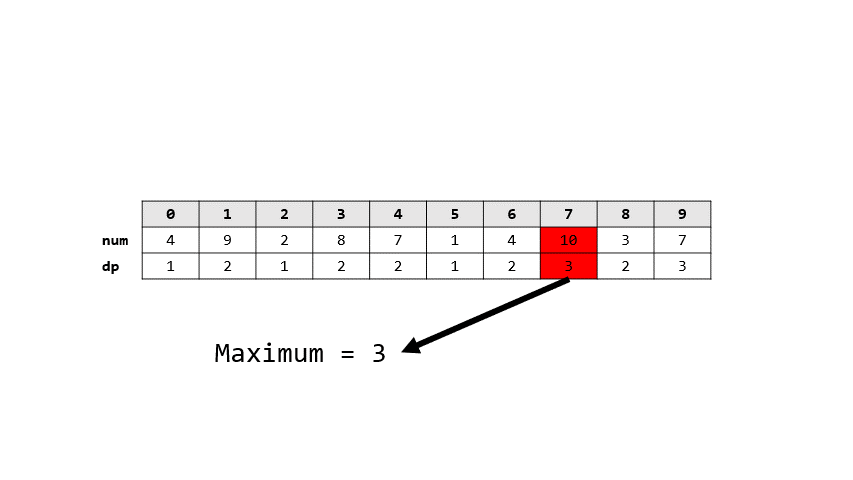
> 答案: 3
### 第2題: leetcode 376 延伸
[leetcode 376](https://leetcode.com/problems/wiggle-subsequence/)
- 程式碼
- 網路大多數的作法
:::spoiler C++
```C++=
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
int size = nums.size();
vector<int> dp(size, 1);
int lastPositive = 0;
int lastNegative = 0;
for (int i=1; i<size; i++){
int DIFF = nums[i] - nums[i-1];
if (DIFF < 0) {
dp[i] = dp[lastPositive] + 1; //This Time is Negative => So Last time must Be Postive
lastNegative = i;
}
else if (DIFF > 0){
dp[i] = dp[lastNegative] + 1; // This Time is Positive => So Last Time must be Negative
lastPositive = i;
}
}
int MAX = 0;
for_each(dp.begin(),dp.end(),[&](const auto & num){MAX=max(MAX,num);});
return MAX;
}
};
```
:::
- 學姊的做法
:::spoiler Python
```python=
class Solution:
def wiggleMaxLength(self, nums: List[int]) -> int:
if not nums: return 0
n = len(nums)
UP = []
DOWN = []
UP.append(nums[0])
DOWN.append(nums[0])
for i in range(1,n):
diff = nums[i] - nums[i-1]
if diff > 0:
UP = DOWN + [nums[i]]
elif diff < 0:
DOWN = UP + [nums[i]]
return max(len(UP),len(DOWN))
```
:::
- 執行結果

- 圖解
- 網路的作法
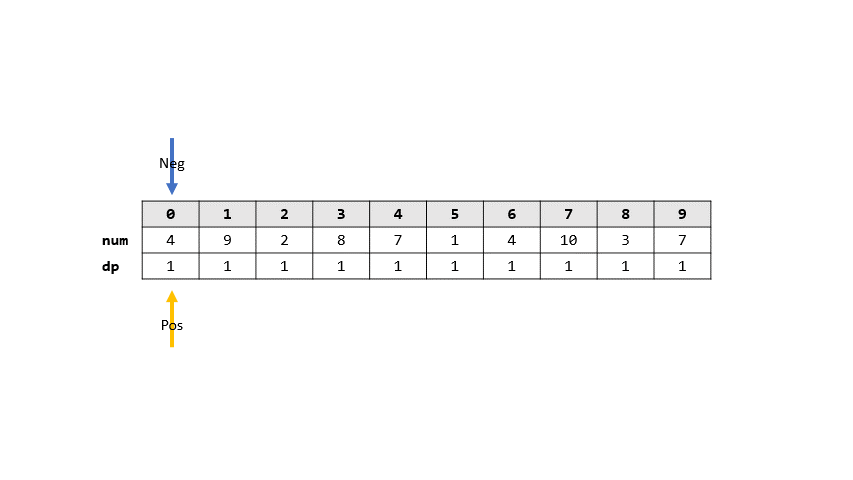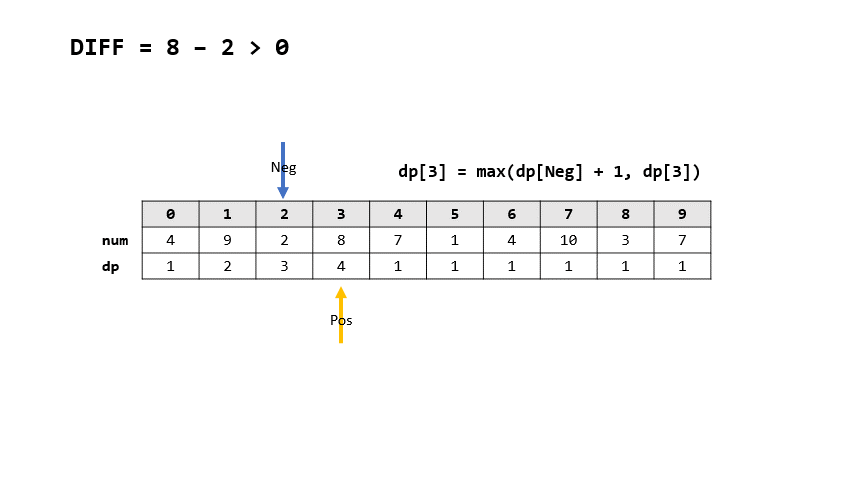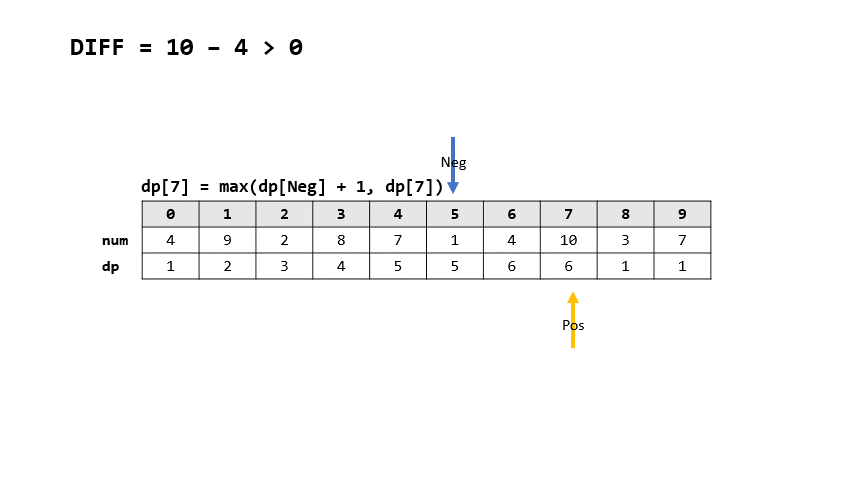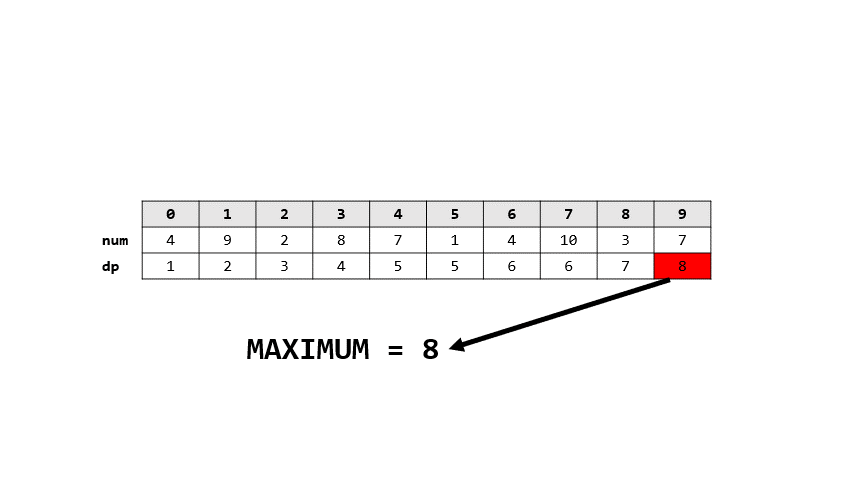
- 解法
- $dp[i]$,從0到i有幾個搖擺數列
- 然後搖擺數列就代表,如果將$num[i] - num[i-1]$一定是正負正負交替,所以這次正下次必然負,反之亦然
- 所以轉移式就是
- 如果現在相減為負
- $dp[i] = max(dp[上一個正]+1, dp[i])$
- 上一個負改成i
- 如果現在相減為正
- $dp[i] = max(dp[上一個負]+1, dp[i])$
- 上一個正改成i
- 學姊的作法
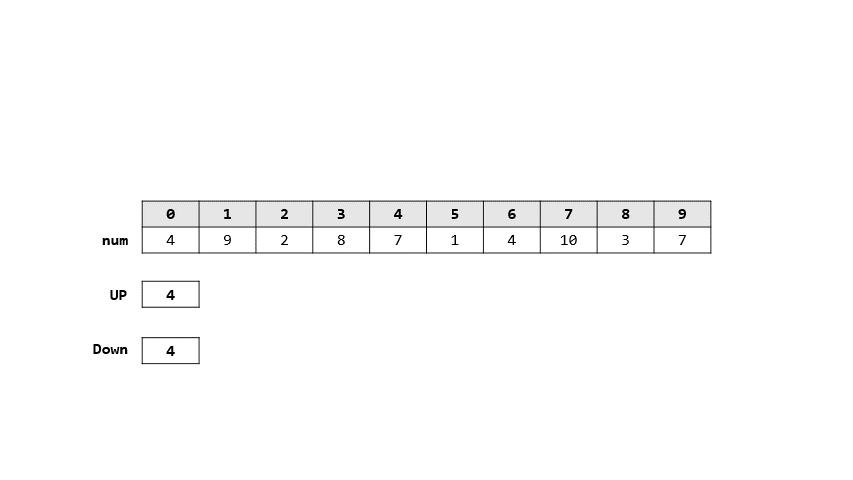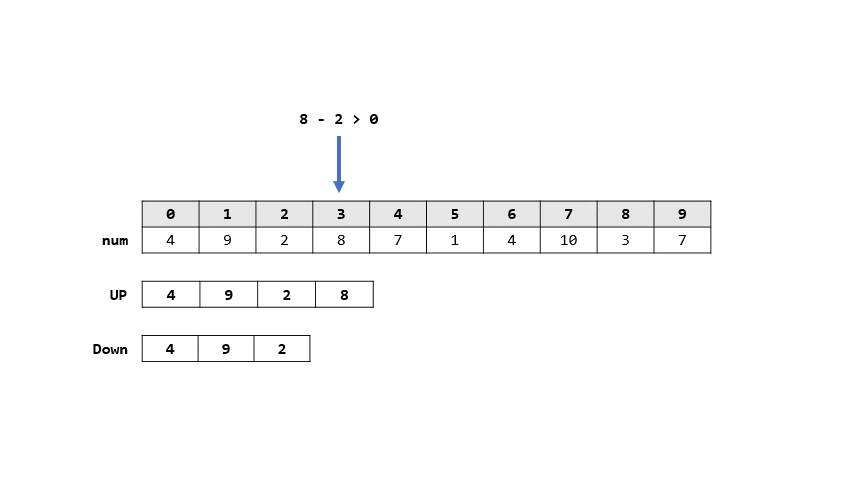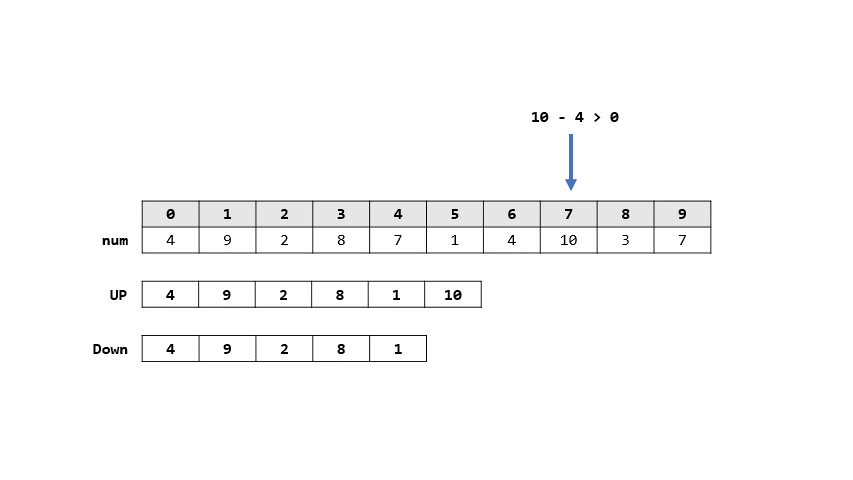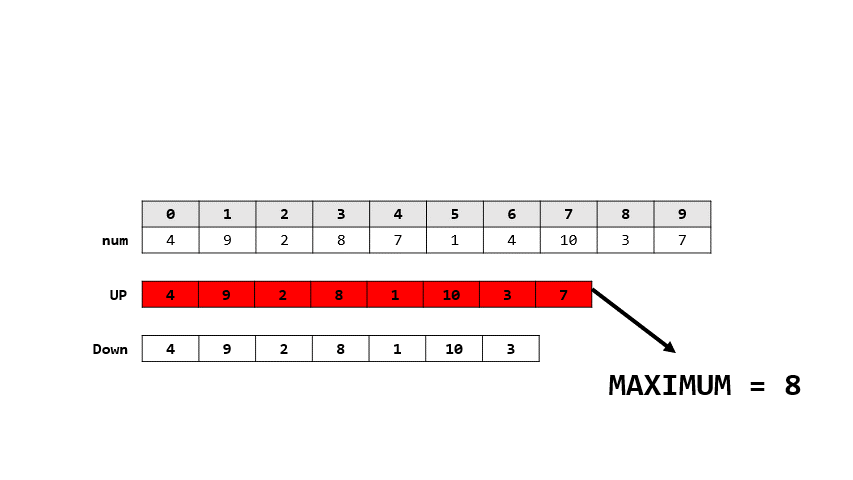
- 解法
- 開兩個陣列
- UP表示: 差以正結束
- DOWN表示: 差以負結束
- 則每一輪如果跟上數差
- 正: 代表上一個一定是負
- UP = DOWN + [num]
- 負: 代表上一個一定是正
- DOWN = UP + [num]
> 答案: 8
### 第3題: leetcode 53 延伸
[leetcode 53](https://leetcode.com/problems/maximum-subarray/description/)
- 程式碼
:::spoiler C++
```C++=
class Solution {
public:
int maxSubArray(const vector<int>& nums) {
int n = nums.size();
vector<int> dp(n,0);
dp[0] = nums[0];
for (int i=1; i<n; i++){
dp[i] = max(dp[i-1]+nums[i],nums[i]);
}
int MAX = 0x80000000;
for_each(dp.begin(),dp.end(),[&](const auto num){MAX=max(num,MAX);});
return MAX;
}
};
```
:::
- 執行過程

- 解法
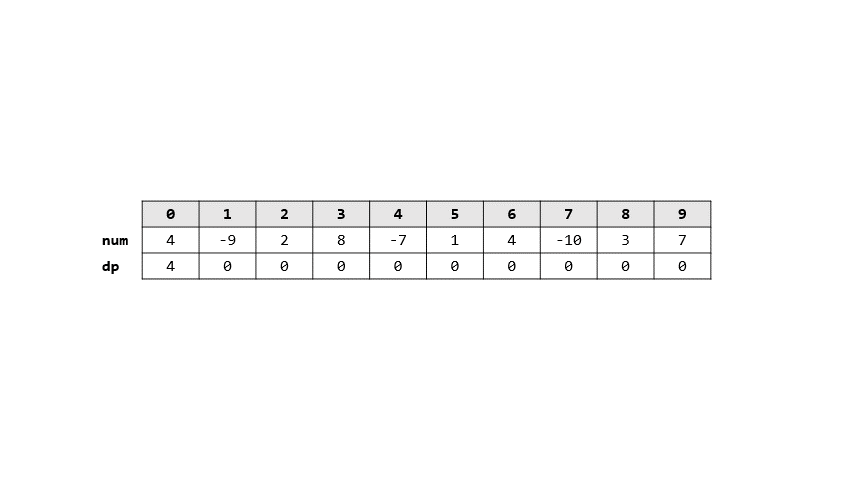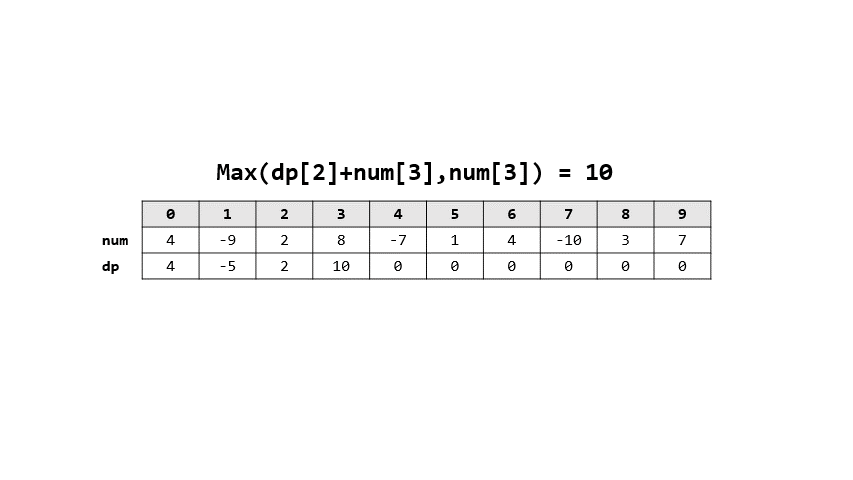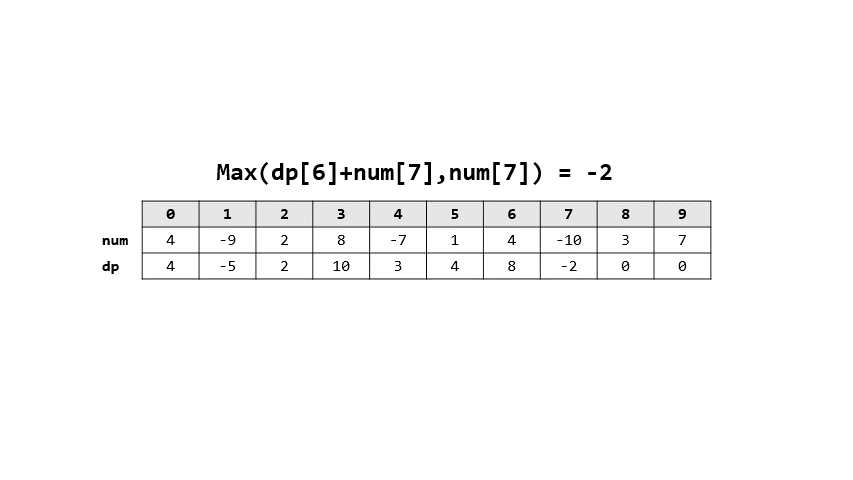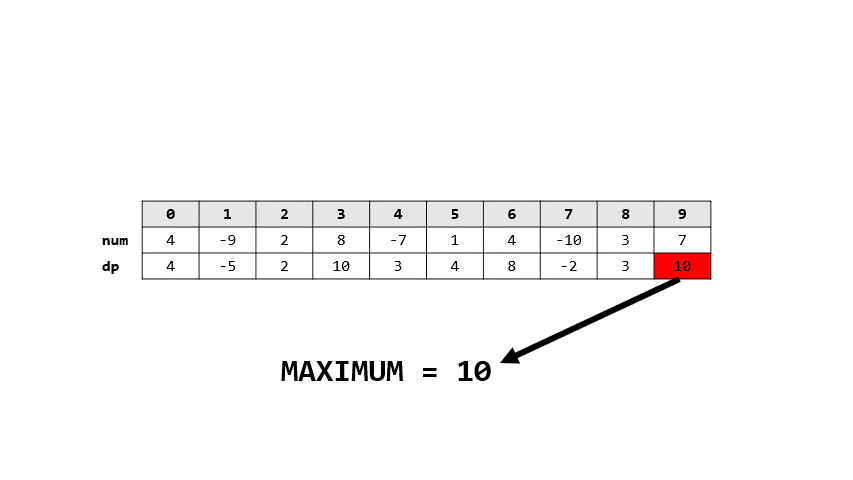
- 用$dp[i]$代表從0到i的最大總和
- 則可以看成要不要和上一個最大和相加
- 也因此轉移式: $dp[i] = max(dp[i-1]+num[i],num[i])$
- 圖解
:::spoiler 6/7未更改題目
- 執行過程

- 解法
- 用$dp[i]$代表從0到i的最大總和
- 則可以看成要不要和上一個最大和相加
- 也因此轉移式: $dp[i] = max(dp[i-1]+num[i],num[i])$
>答案: 55
:::
## 程式題
### 第4題: 乘積最大的連續子序列
[leetcode 152](https://leetcode.com/problems/maximum-product-subarray/)
- 程式碼
- ~~我真的要靠北這題,用long long你的測試資料會卡在一堆10的那個,我人生第一次開double在整數...,因為double可以存的更多(1.7E +/- 308),真是謝囉~~
:::spoiler C++
```C++=
class Solution {
public:
int maxProduct(const vector<int>& nums) {
const int n = nums.size();
double maxProduct = 1;
double minProduct = 1;
vector<int> dp(n,INT_MIN);
if (nums[n-1] == 0){
dp[n-1] = 0;
}
else{
dp[n-1] = nums[n-1];
maxProduct = nums[n-1];
minProduct = nums[n-1];
}
for (int i=n-2; i>=0; i--){
double res = dp[i+1];
if (nums[i] == 0){
dp[i] = res>0? res: 0;
maxProduct = 1;
minProduct = 1;
}
else{
double tmp = maxProduct;
maxProduct = std::max({maxProduct*nums[i],minProduct*nums[i],(double )nums[i]});
minProduct = std::min({tmp*nums[i],minProduct*nums[i],(double )nums[i]});
res = std::max(res, maxProduct);
dp[i] = res;
}
}
return dp[0];
}
};
```
:::
- 執行過程

- 完成程度: 有參考他人
- [ref](https://leetcode.com/problems/maximum-product-subarray/solutions/5067595/beginner-friendly-diagram-4-solutions-step-by-step-classic-backtracking-and-dp-approach/)
- [關於爆掉的問題](https://leetcode.com/problems/maximum-product-subarray/solutions/5270100/2024-and-runtime-error-i-got-you/)
- 花費時間: 1.5小時(測資RRRRRR)
- 思路
- 其實和第三題很像
- 我們有三個動作,看上一輪最小的乘以現在,看上一輪最大乘以現在,或是什麼都不乘
- 為什麼有最小的
- 因為最小可能是負數,可能下一位是負,所以我們也要存一下
- 那就解出來了
- $maxProduct = max(maxProduct*num[i],minProduct*num[i],num[i])$
- $minProduct = min(maxProduct*num[i],minProduct*num[i],num[i])$
- dp[i] = maxProduct
### 第5題: 找零錢
[leetcode 332](https://leetcode.com/problems/coin-change/description/)
- 程式碼
:::spoiler C++
```C++=
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(1 + amount,0x7FFFFFFE);
dp[0] = 0;
for (int i=1; i<=amount; i++){
for (const auto & coin: coins){
if (i-coin>=0){
dp[i] = min(dp[i],dp[i-coin]+1);
}
}
cout<<dp[i]<<" ";
}
if (dp[amount] == 0x7FFFFFFE) return -1;
return dp[amount];
}
};
```
:::
- 執行結果

- 完成程度: 靠自己
- 花費時間: 10分鐘(大一有寫過好開心)
- 思路
- $dp[i]$代表找i元要的錢
- 則$dp[i] = min(dp[i],dp[i-coin]+1)$
- 如果$i-coin<0$則轉移式不會作用
- 補充
- 為什麼不能用貪心呢
- 貪心三大條件
1. 有明確的階段
2. 該階段最佳
3. 最終結果最佳
- 好但是找錢問題中,若各錢幣不是整數倍的關係
- 以coin=[1,8,10],如果找25$
- 貪心解: 10 * 2 + 1 * 5 = 25 => 7個硬幣
- 但最佳解: 8 * 3 + 1 = 24 => 4個硬幣
- 也因此在這邊可以發現各個子問題有相關性,因此無法貪
### 第6題: 子集合
[leetcode 78](https://leetcode.com/problems/subsets/description/)
- 程式碼
:::spoiler C++
```C++=
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> res;
function<void(int, vector<int>&)> dfs = [&](int index, vector<int>& subset){
res.push_back(subset);
for (int i=index; i<n; i++){
subset.push_back(nums[i]);
dfs(i+1,subset);
subset.pop_back();
}
};
vector<int> subset;
dfs(0,subset);
return res;
}
};
```
:::
- 執行結果

- 完成程度: 有參考別人
- [ref](https://www.youtube.com/watch?v=3JWtSMlq0Sw)
- 花費時間: 30分鐘
- 思路
- 其實這題跟排列很像...,~~我是白癡謝謝大家~~
- 其實就是使用回朔法
- 首先每一個節點都加入其中
```C++=
res.push_back(subset);
```
- 然後開始造訪子節點
```C++=
for (int i=index; i<n; i++){
subset.push_back(nums[i]); // next Child
dfs(i+1,subset);
subset.pop_back(); // Go back to father
}
```
## 心得
終於寫完作業了,希望明年不要重修舊好🤡🤡🤡🤡
這周學了回朔法,印象中資工系一定下的棋八皇后(不是OTHELLO),就是用這個概念寫的。雖然說起來簡單,但每次寫回朔法都卡卡的,我可能要多練習了QQ。
作業的部分,這周是leetcode大全吧...,寫leetcode寫到想哭,尤其第四題,測資到底是!@#$%^&,好我應該乖乖用python。
最後每周地獄作業結束,真開心(才怪網路程式設計跟圖學還沒做完,崩潰)
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet