# 演算法第13周
## 觀念題
### 第1題: shortest path in multi-stage graph
- forward approach

:::spoiler python
```python=
INF = float('inf')
node, edge = [int(x) for x in input().split()]
graph = [[INF for _ in range(node)] for _ in range(node)]
for i in range(edge):
u, v, w = [int(x) for x in input().split()]
graph[u-1][v-1] = w
for row in graph:
for elem in row:
print(elem, end='\t')
print()
def shortestPath(graph):
node = len(graph)
dist = [0] * node
for i in range(1,node):
dist[i] = INF
for j in range(node):
if graph[j][i] != INF:
dist[i] = min(dist[i], graph[j][i] + dist[j])
return dist[node-1]
print(shortestPath(graph))
```
:::
- 過程
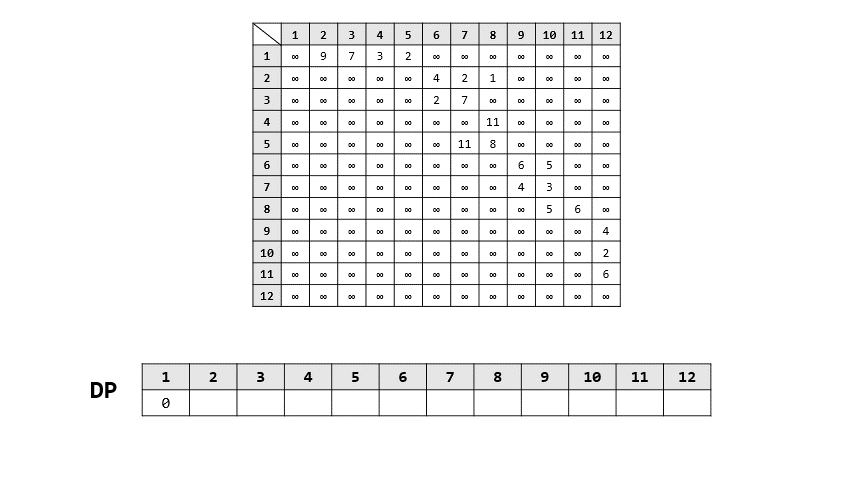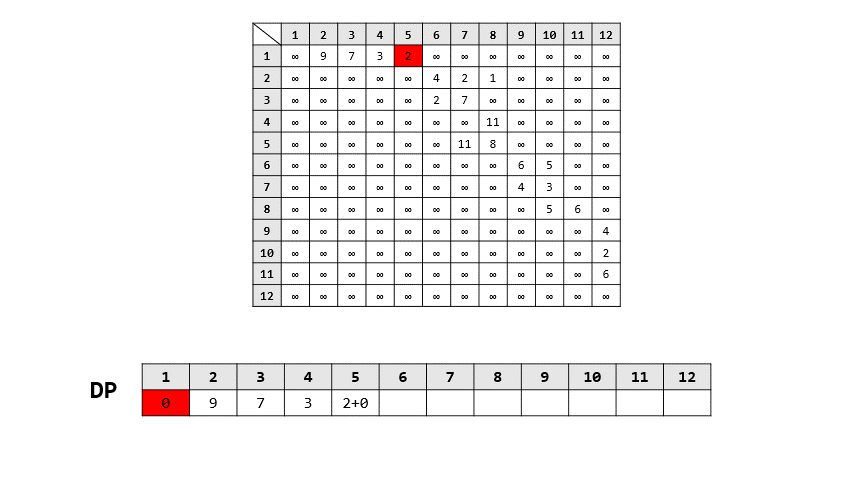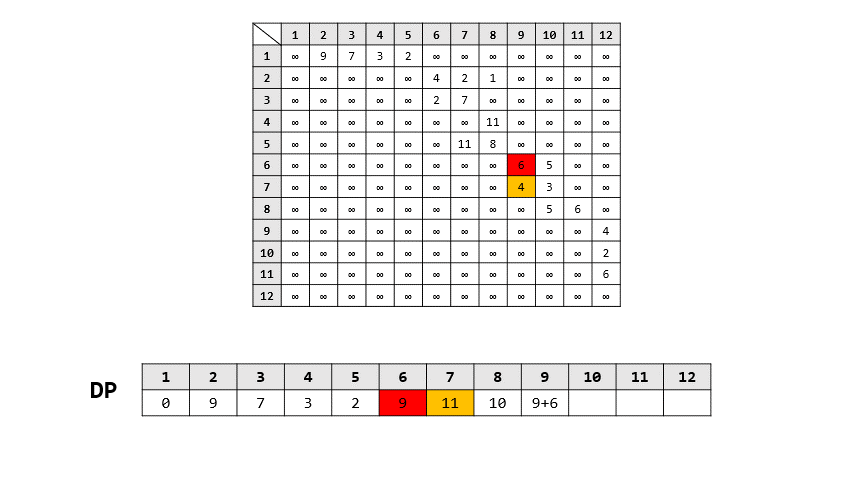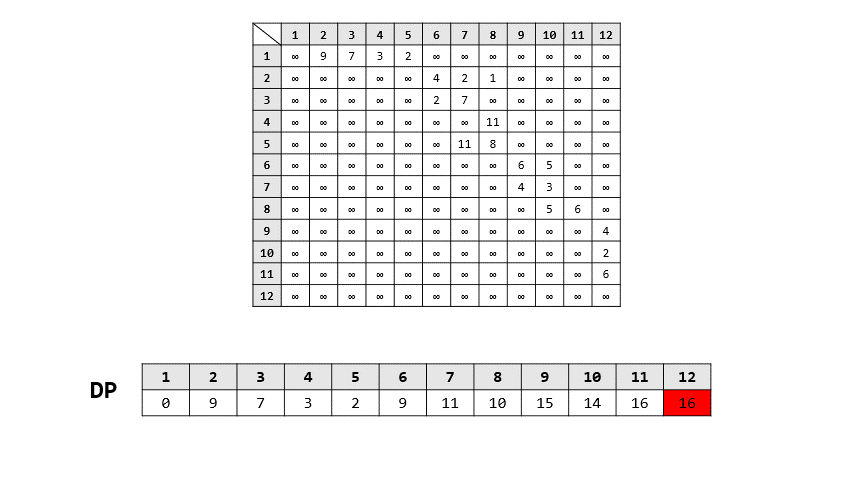
- backward approach

:::spoiler Python
```python=
INF = float('inf')
node, edge = [int(x) for x in input().split()]
graph = [[INF for _ in range(node)] for _ in range(node)]
for i in range(edge):
u, v, w = [int(x) for x in input().split()]
graph[u-1][v-1] = w
def shortestPath(graph):
node = len(graph)
dist = [0] * node
for i in range(node-2,-1,-1):
dist[i] = INF
for j in range(node):
if graph[i][j] != INF:
dist[i] = min(dist[i], graph[i][j] + dist[j])
return dist[0]
print(shortestPath(graph))
```
:::
- 過程
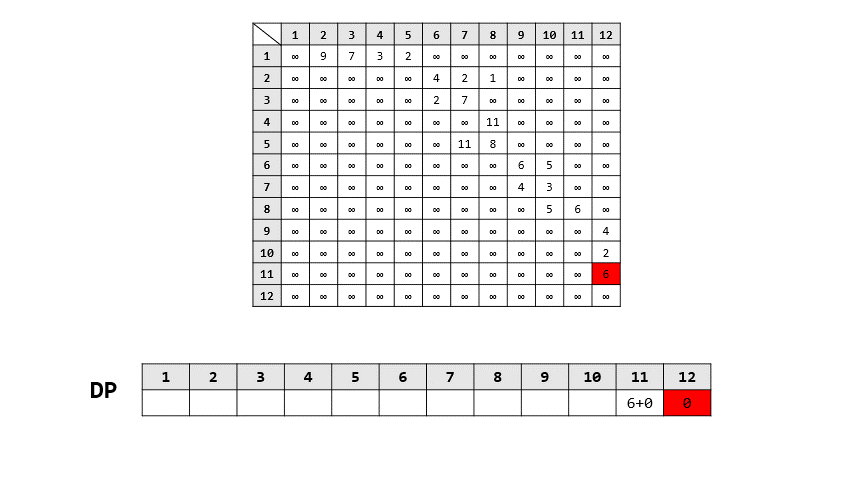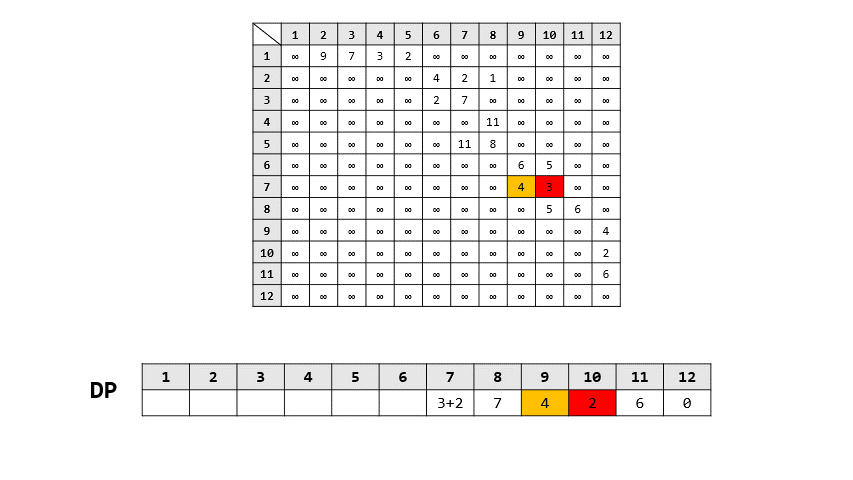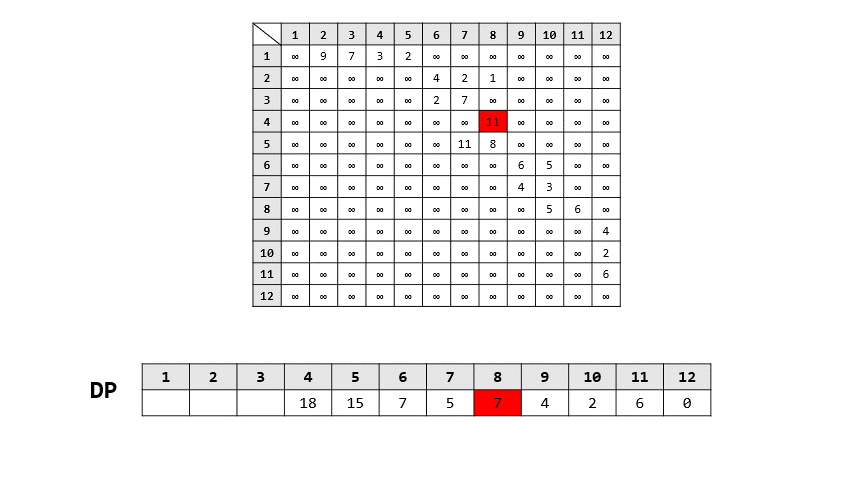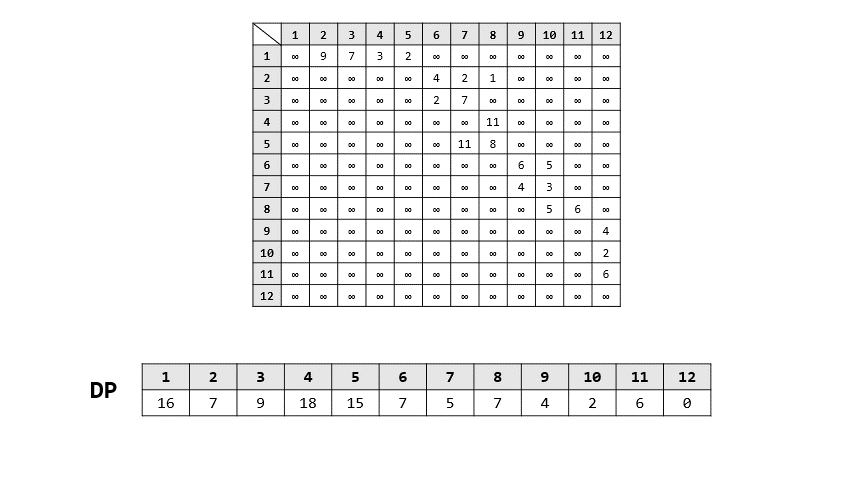
> 答案: 16
> 路徑: 1 -> 3 -> 6 -> 10 -> 12
### 第2題: leetcode70延伸
:::info
**前情提要**
[leetcode 70](https://leetcode.com/problems/climbing-stairs/)
- 阿就費式數列阿
:::spoiler C++
```C++=
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n+1,0);
dp[0] = 1;
dp[1] = 1;
for (int i=2;i<=n;i++){
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
};
```
:::
:::
- 程式碼
~~我可以只交程式碼嗎~~
:::spoiler Python
```python=
n = int(input('多少階梯? '))
dp = [0] * (n+1)
dp[0] = 1
dp[1] = 1
dp[2] = 2
for i in range(3,n+1):
dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
print(f"Step: {dp[n]}")
```
:::
- 執行結果

- 過程說明
- 首先,把轉移式列出來
- $dp[i]=dp[i-1]+dp[i-2]+dp[i-3]$
- 然後列出起始條件
- $dp[0] = 1$ -> 爬上0個階層也是一種方法
- $dp[1] = 1$
- $dp[2] = 2$ -> (1,1) and (2)
- 最終解
- $dp[n]$
- 過程
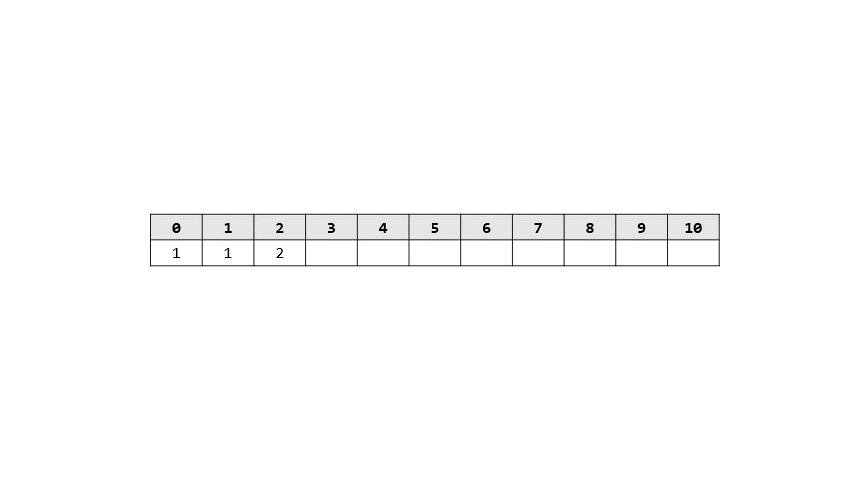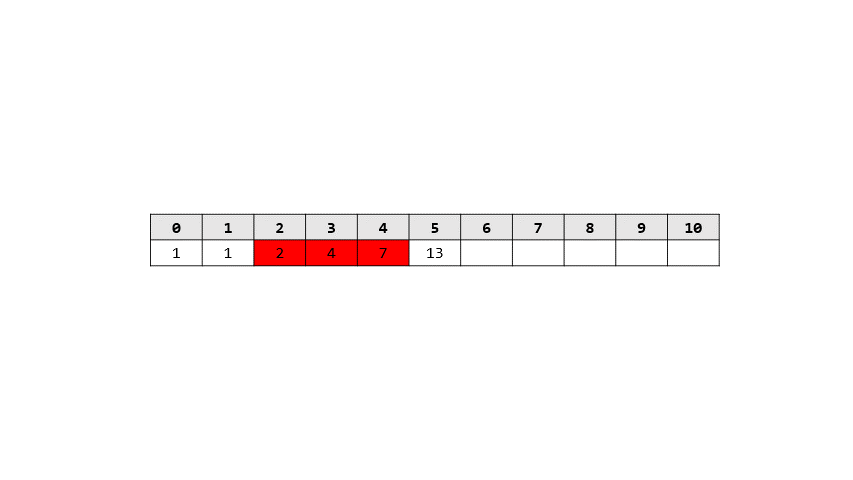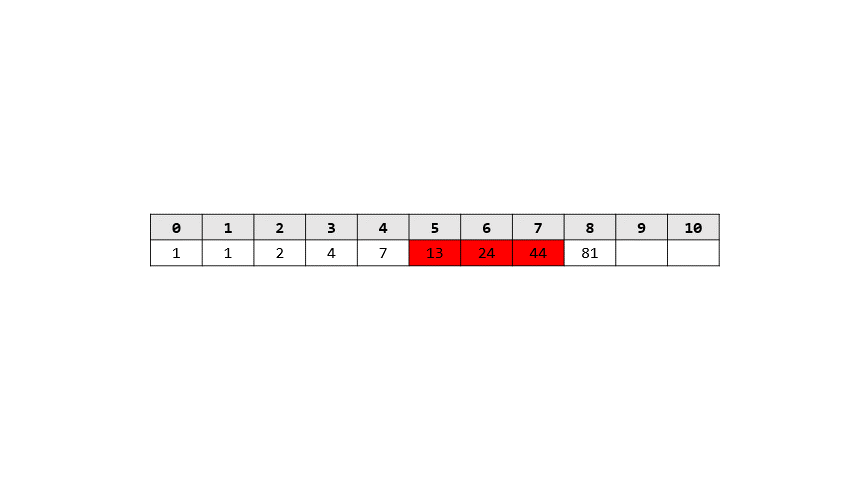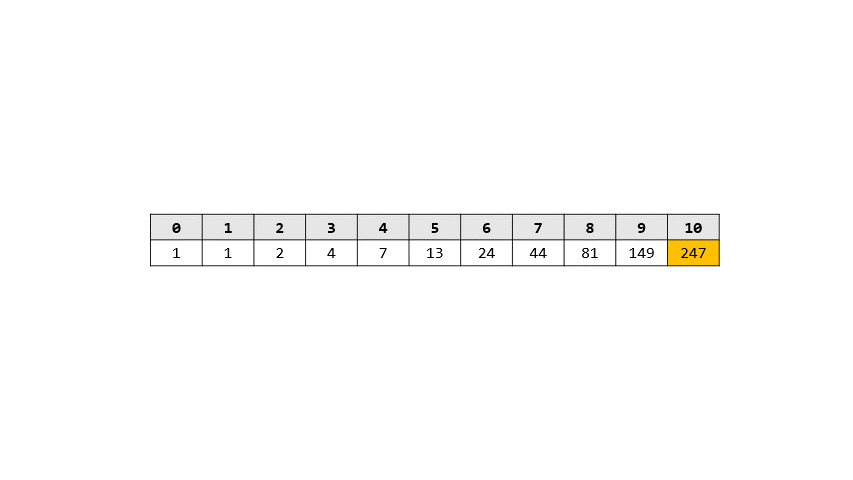
> 答案: 274
### 第3題: Leetcode 1395應用
[leetcode 1395](https://leetcode.com/problems/count-number-of-teams/)
- 解法一: 2D DP
- 程式碼
~~我可以只交程式碼嗎畫圖好累,殺了我~~
:::spoiler C++
```C++=
class Solution {
public:
int numTeams(vector<int>& rating) {
int n = rating.size();
vector<vector<int>> inc_dp(4,vector<int>(n,0));
vector<vector<int>> dec_dp(4,vector<int>(n,0));
for (int i=0; i<n; i++){
inc_dp[1][i] = 1;
dec_dp[1][i] = 1;
}
for (int i=2; i<4; i++){
for (int j=0; j<n; j++){
for (int k=0; k<j; k++){
if (rating[j] > rating[k])
inc_dp[i][j] += inc_dp[i-1][k];
else
dec_dp[i][j] += dec_dp[i-1][k];
}
}
}
int sum = 0;
for_each(inc_dp[3].begin(),inc_dp[3].end(), [&](const auto & i){sum+=i;});
for_each(dec_dp[3].begin(),dec_dp[3].end(), [&](const auto & i){sum+=i;});
return sum;
}
};
```
:::
- 執行結果

- 執行過程
- 首先先理解幾點
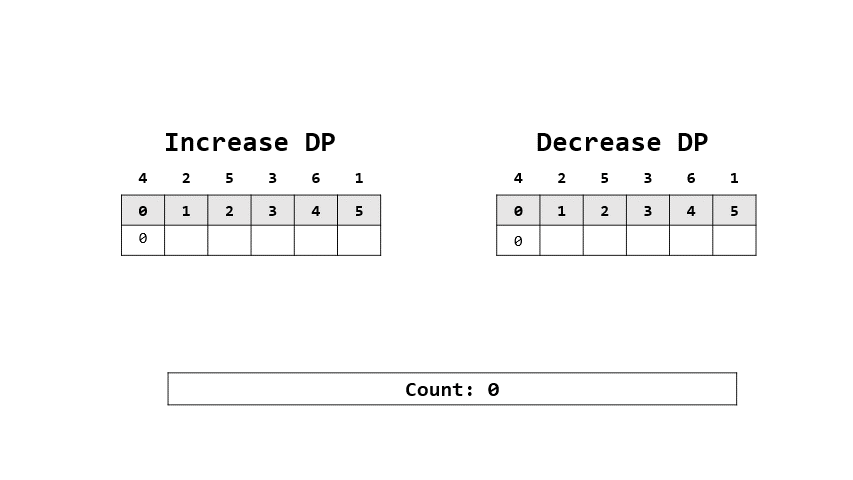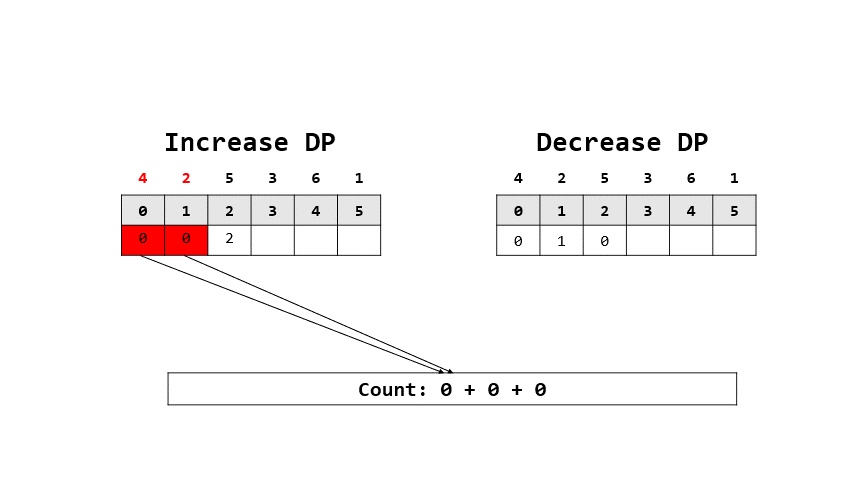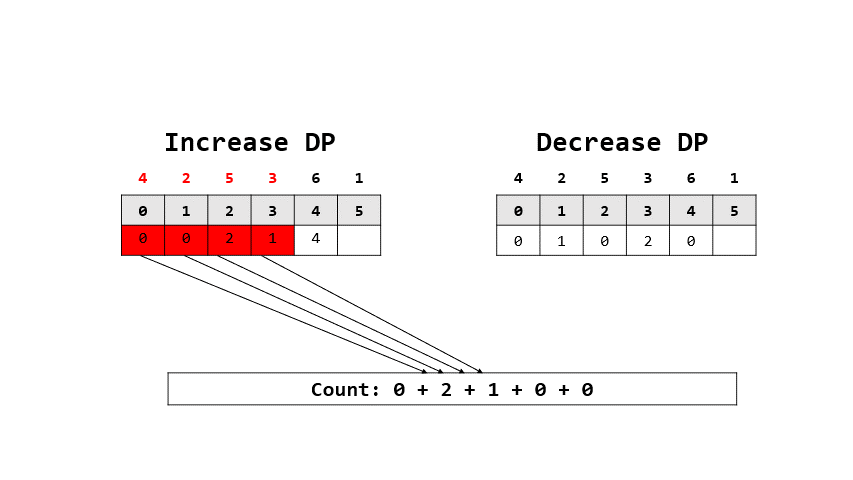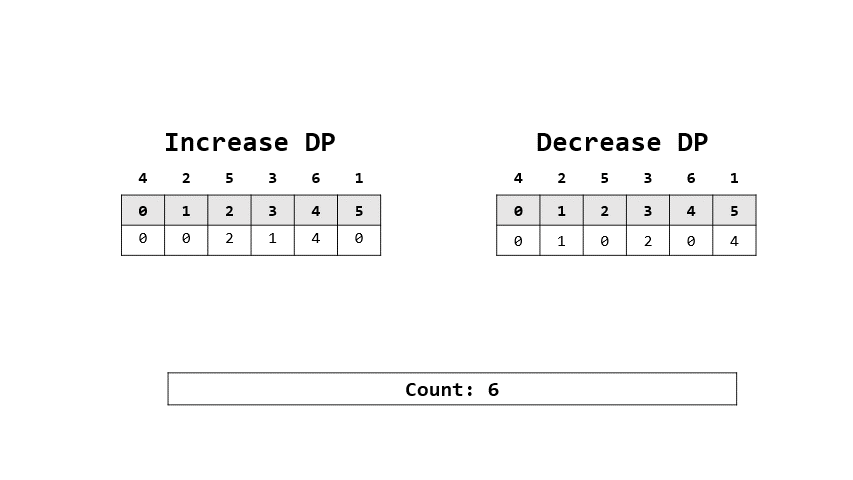
1. $dp[i][j]$含意: $i$代表著連續遞增or遞減幾個數字,$j$代表一定有第$j$個數字
2. 因此我們可以用過去連續次數連加上現在新加入的元素,也就是假如一個數列$[1,2,3,4]$
- 有兩個數列遞增的可能是
- (1 , 2), (2 , 3), (1,3)
- 那如果是這樣,新加入的數字4是不是直接跟最大的比較就好了
- (1,2,4), (2,3,4), (1,3,4)
3. 注意一下其實我這邊分成兩個表,一個是遞增dp,一個是遞減dp,但因為邏輯差不多,所以看起來類似
- 可以做轉移式了(這邊以遞增表作舉例,遞減表反之)
- $dp[i][j] = sum(dp[i-1][x])\space \forall x\in[0,j) \space\space\space\space if \space\space\space\space arr[j] < arr[x]$
- 初始條件
- $dp[i] = [1]*n$
- 最終解
- $\Sigma dp[3][i]$
- 過程

- 解法二: 1D DP
- 就是老師的作法
- 程式碼
:::spoiler Python
```Python=
class Solution:
def numTeams(self, rating: List[int]) -> int:
n = len(rating)
smallerDP = [0 for _ in range(n)]
lagerDP = [0 for _ in range(n)]
count = 0
for i in range(n):
for j in range(i):
if rating[j] < rating[i]:
count += smallerDP[j]
smallerDP[i] += 1
else:
count += lagerDP[j]
lagerDP[i] += 1
return count
```
:::
- 執行結果

- 執行過程
- 其實就是解法一優化過程
- 如果觀察一下剛剛的數列可以看到一件事,`inc_dp[1]` 與 `dec_dp[1]`其實就是找有幾個數字比他小or大,所以我們已經有足夠的線索拼出轉移式了(這邊以larger做舉例)
- $lagerDP[i]=num(arr[i]>arr[j]) \forall i>j$
- 然後假如成立我們還可以順便算出加入這個數組時有多少可能
- 只能說,想到這個的太電了:place_of_worship::place_of_worship::place_of_worship::place_of_worship::place_of_worship::place_of_worship::place_of_worship::place_of_worship::place_of_worship:
- 過程
> 答案: 6
## 實作題
### 第4題: 計算正方形數量
[leetcode 1277](https://leetcode.com/problems/count-square-submatrices-with-all-ones/)
- 程式碼
:::spoiler C++
```C++=
// fast IO
static auto __ = []()
{
std::ios_base::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
return 0;
}();
class Solution {
public:
int countSquares(vector<vector<int>>& matrix) {
int row = matrix.size();
int col = matrix[0].size();
int count = 0;
for (int i=0;i<row;i++){
for (int j=0;j<col;j++){
if (i!=0 && j!=0 && matrix[i][j] != 0)
matrix[i][j] += min({matrix[i-1][j],matrix[i][j-1],matrix[i-1][j-1]});
count+=matrix[i][j];
}
}
return count;
}
};
```
:::
- 執行結果

- 花費時間: 體感1.5小時
- 完成程度: 有參考別人
- [ref](https://leetcode.com/problems/count-square-submatrices-with-all-ones/solutions/2363854/3-solutions-recursion-memoization-tabulation-easy-to-understand/)
- 思路
- 首先呢,我們可以先定義$dp[i][j]$為從(i,j)到(0,0)有多少長方形
- 那如果這邊是1代表,可以在擴展長方形
- 如果可以擴展,那哪三處可以擴展
- 上面,左邊,斜上方
- 代表`dp[i][j] += min(up,left,upper left)`
- 所以,轉移式來囉
- $dp[i][j]+= min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]) \space \space\space if \space\space\space dp[i][j]=1$
- 答案是將全部總和
### 第5題: 所有可能的合法成對括號
[leetcode 22](https://leetcode.com/problems/generate-parentheses/)
- 程式碼
- 作法一: DFS
- 程式碼
:::spoiler C++
```C++=
// fast IO
static auto __ = []()
{
std::ios_base::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
return 0;
}();
class Solution {
public:
vector<string> generateParenthesis(int n) {
int LP=0, RP=0;
vector<string> ans;
function<void(int, int, string)> slove = [&](int LP,int RP, string s){
if (s.size() == 2*n){
ans.push_back(s);
return;
}
if (LP<n) slove(LP+1,RP,s+'(');
if (LP>RP) slove(LP,RP+1,s+')');
};
slove(LP,RP,"");
return ans;
}
};
```
:::
- 執行結果

- 花費時間: 30分鐘
- 完成程度: 有參考別人
- [ref](https://www.cnblogs.com/grandyang/p/4444160.html)
- 思路
- 這題用回朔法概念解
- 所以呢我們就先加入左括號
- 如果當前的狀態左括號比較多,那就加入右括號
- 然後假如當前字符長度已經達到2*n,就可以當成答案了
- 作法二: DP
- ~~90%是被王老闆跟張紹維嘴用遞迴,然後賭氣寫DP~~,結果根本通靈不了,我願稱其是大通靈程式設計
- 程式碼
:::spoiler C++
```C++=
// fast IO
static auto __ = []()
{
std::ios_base::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
return 0;
}();
class Solution {
public:
vector<string> generateParenthesis(int n) {
unordered_map<int, unordered_set<string> > ans;
ans[1] = {"()"};
for (int i=2; i<=n; i++){
unordered_set<string> tmp;
// ADD s[i-j] and s[j]
for (int j=1; j<i; j++){
for (const auto &s1: ans[i-j]){
for (const auto &s2: ans[j]){
tmp.insert(s1+s2);
}
}
}
// ADD (+s[i-1]+)
for (const auto &s: ans[i-1]){
tmp.insert("("+s+")");
}
// push in dp array
ans[i] = tmp;
}
return vector<string>(ans[n].begin(),ans[n].end());
}
};
```
:::
- 執行結果

- 花費時間: 體感2小時:derelict_house_building:
- 完成程度: 參考別人的程式碼
- [ref 1](https://leetcode.com/problems/generate-parentheses/solutions/2610178/22-generate-parentheses/)
- 思路
- 首先,可以這樣思考
- 上一個狀態只要前後加上括號就是其中一解
- 枚舉全部可能,可以使$a+b=i$,只要字串接合就是答案
- 所以有了這些我們可以做成轉移式了
- $dp[i] = '(' + dp[i-1] + ')'$
- $dp[i] = dp[a] + dp[b]$ $\forall a+b=i$
- 接下來初始狀態就很簡單了
- $dp[1] = "()"$
### 第6題: 巴士卡三角形
[leetcode 118](https://leetcode.com/problems/pascals-triangle/description/)
- 解法
- ~~為什麼這邊改用Rust呢,因為解法二用Racket就有兩個R了~~
- 做法一: 使用GIF的作法
- 程式碼
:::spoiler Rust
```rust=
impl Solution {
pub fn generate(num_rows: i32) -> Vec<Vec<i32>> {
let mut dp: Vec<Vec<i32>> = Vec::with_capacity(num_rows as usize);
for i in 0..num_rows as usize{
let mut row:Vec<i32> = vec![1; i+1];
for j in 1..i{
row[j] = dp[i-1][j-1] + dp[i-1][j];
}
dp.push(row);
}
dp
}
}
```
:::
- 執行結果

- 花費時間: 30分鐘
- 完成程度: 靠自己(還是要說leetcode題目已經把解法寫出來了...)
- 思路
- ~~題目都給圖了笑死~~
- 
- 好反正就是轉移式
- $dp[i][j] = dp[i-1][j-1]+dp[i-1][j]$
- 做法二: 使用數學的方法
- ~~其實只是想寫寫看類LISP語言~~
- 程式碼
:::spoiler Racket
```racket=
(require math/number-theory)
(define/contract (generate numRows) (-> exact-integer? (listof (listof exact-integer?)))
(map
( lambda (i)
(map (curry binomial i) (range (+ 1 i)))
)
(range numRows)
)
)
```
:::
- 執行結果

- 花費時間: 1小時
- ~~我就不該寫這種神經病語言~~
- 完成程度: 有參考他人的程式碼
- ~~其實就是我根本不會LISP~~
- [ref](https://leetcode.com/problems/pascals-triangle/solutions/3031455/simple-racket-solution/)
- 思路
- 好反正就是數學的問題,跟DP沒關西
- 
## 心得
今天學了DP,寫完那題爬樓梯才想到大一的程式設計考手寫扣,題目是費氏數列,然後我開陣列寫,被老師說我偷吃步她還沒教array:(,原來那時候被我稱為開陣列的方式就是動態規劃。
這周的作業我深刻體會到了DP靠通靈,難怪系程式第一名的陳同學和張同學都說,DP靠通靈,只能說不要在外面說你會DP,因為可能通靈不出來;(。
雖然說前面一直在diss DP,但老實說,DP這個解法確實會幫你省很多時間,我平常用遞迴的問題換成DP效率確實有高上許多,他真是讓人又愛又恨^^。
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet