# [AirVO](https://github.com/xukuanHIT/AirVO)

An Illumination-Robust Point-Line Visual Odometry

[Demo](https://youtu.be/5zn_Q2KJlBI)

# Introduction

- Current <abbr title="Visual Odometry">VO</abbr> systems are fragile to dynamic illumination environments
- Deep learning feature extraction & matching methods are robust to dynamic illumination which can help

## Contributions

- AirVO employ deep learning features + traditional optimization
- Run at 15Hz on Nvidia Jetson AGX Xavier (2018)
- Match 2D line features with 2D keypoints but without line descriptors

# Related Works

## Feature Extraction and Tracking for Visual SLAM

1. Traditional keypoint extraction methods
- E.g. ORB, FAST, BRISK
- 👎: Suffer from dynamic illumination, thus the <abbr title="Simutaniously Localization And Mapping">SLAM</abbr> systems using them also affected
2. Deep learning approaches
- Using e.g. TFeat network, SuperPoint, LIFT
- 👎: Extracted features are still match by traditional way that still affected by changing illumination

## Visual SLAM for Dynamic Illumination

1. Model local or global brightness change (& jointly optimize)
- E.g. <abbr title="Zero-mean Normalized Cross Correlation">ZNCC</abbr>, <abbr title="Locally-scaled Sum of Squared Differences">LSSD</abbr>
- 👎: But lighting change on different scenes' areas differently
2. Using multiple feature & other methods
- If a kind of feature fail, use another feature

# Methodology

## System Overview

- Track current frame with last keyframe
- CNN (SuperPoint) to extract features
- GNN (SuperGlue) to match features
- Point-line association with distance & match lines with their matched points
- FP16 NNs run on GPU
- Multi-treading utilizes both CPU & GPU
- Track & map with stereo frame while keyframe created

<figure>


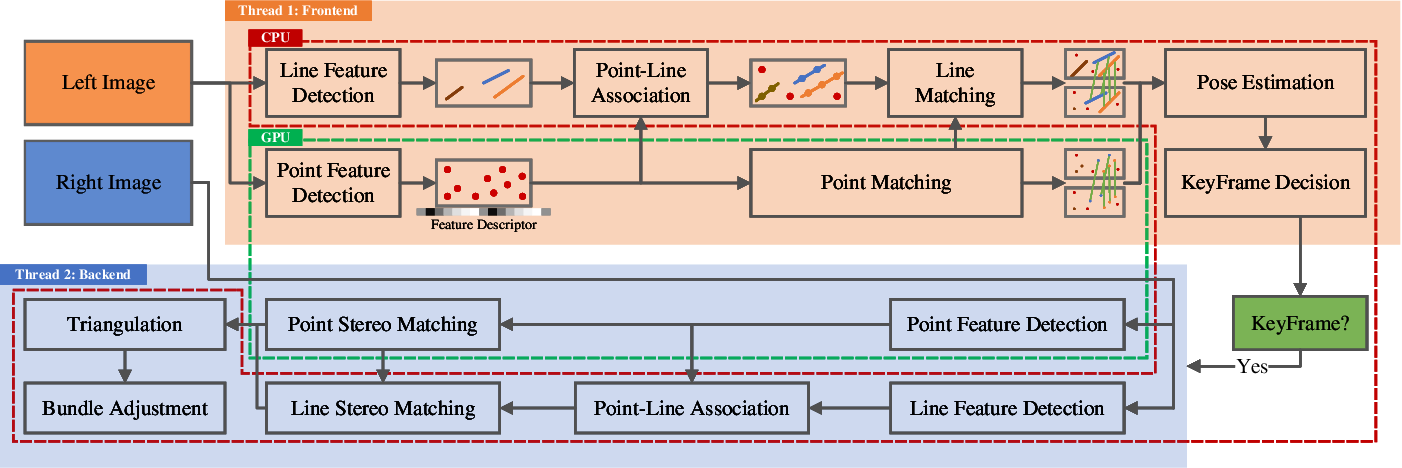
<figcaption>

AirVO framework

</figcaption></figure>

## 2D Line Processing

### Detection

1. Use <abbr title="Line Segment Detector">LSD</abbr>^{[\[1\]](#fn1)}
2. Merge line segments
- If angular & distance of midpoint < threshold
- If projection on X & Y axis don't overlap & endpoints' distance is close
3. Get long line
- $\because$ long line segments are repetitive & robust to noise
- Deprecate if length < threshold

<figure>


<figcaption>

w/o & w/ merging & filtering line segments

</figcaption></figure>

### Matching

1. Point matching: $\because$ CNN extracted feature is illuminance robust, $\therefore$ use them to match lines
2. Point-line association: if point-line distance < threshold
3. Line matching: if $S_{mm}$ & $N_{pm}$ \> threshold
- $N_{pm}$: #match points between line segment $^{k}\mathbf{l}_{m}$ & $^{k+1}\mathbf{l}_{n}$
- $^{k}N_{m}$ & $^{k+1}N_{n}$: #points $\in \ ^{k}\mathbf{l}_{m}$ & $^{k+1}\mathbf{l}_{n}$
- $S_{m n}=\frac{N_{p m}}{\min \left({ }^k N_m,{ }^{k+1} N_n\right)}$

<figure>


<figcaption>

Line matching results

</figcaption></figure>

## 3D Line Processing

### Representation

1. Plücker coordinate: for 3D line triangulation, transformation & projection
- $\mathbf{L}=\begin{bmatrix} \mathbf{n} \\ \mathbf{v} \end{bmatrix} \in \mathbb{R}^6$
2. Orthonormal representation: during graph optimization. To reduce DoF & for numerical stability
- $\mathbf{L}=\underbrace{\begin{bmatrix} \frac{\mathbf{n}}{\|\mathbf{n}\|} & \frac{\mathbf{v}}{\|\mathbf{v}\|} & \frac{\mathbf{n} \times \mathbf{v}}{\|\mathbf{n} \times \mathbf{v}\|} \end{bmatrix}}_{\mathbf{U} \in S O(3)} \underbrace{\begin{bmatrix} \|\mathbf{n}\| & \\ & \|\mathbf{v}\| \\ \ \end{bmatrix}}_{\mathbf{W}=\Sigma_{3 \times 2}} \in S O(3) \times S O(2)$

### Triangulation

1. Back-project: a 3D line segment observed on 2 image, $\mathbf{l}_{1}$ & $\mathbf{l}_{2}$, can back-project to 2 3D planes $\pi_{1}$ & $\pi_{2}$. Then the 3D line = intersection of $\pi_{1}$ & $\pi_{2}$
2. Using triangulated 3D points ($\mathbf{X}_{1}, \mathbf{X}_{2}$): when above method fail (because of degenerate motions)
- $\mathbf{L}=\begin{bmatrix} \mathbf{n} \\ \mathbf{v} \end{bmatrix}=\begin{bmatrix} \mathbf{X}_1 \times \mathbf{X}_2 \\ \frac{\mathbf{X}_1-\mathbf{X}_2}{\left\|\mathbf{X}_1-\mathbf{X}_2\right\|} \end{bmatrix}$

### Re-projection

- ${ }_w^c \mathbf{H}$: world $\rightarrow$ camera frame transform matrix
- ${ }_c^i \mathbf{P}$: line projection matrix
- ${ }^i \mathbf{l}$: reprojected 2D line

$$
{ }^c \mathbf{L}=\begin{bmatrix}
{ }^c \mathbf{n} \\
{ }^c \mathbf{v}
\end{bmatrix}={ }_w^c \mathbf{H} {\ }^w\mathbf{L}
,\quad
{ }^i \mathbf{l}=\begin{bmatrix}
A \\
B \\
C
\end{bmatrix}={ }_c^i \mathbf{P} {\ }^c \mathbf{n}

$$

## Keyframe Selection

- $\because$ learning-based point matching can track with long baseline, $\therefore$ track current frame with last keyframe. This can also reduce accumulated drift
- Selection criteria, if current frame...:
- Distance, angle to last keyframe > threshold
- #tracked map points $\in \left[N^{kf}_2, N^{kf}_1 \right]$
- #tracked points > $N^{kf}_2$ but last frame's < $N^{kf}_2$

<figure>


<figcaption>

Epipolar geometry. Baseline is $\overline{O_L O_R}$

</figcaption></figure>

## Graph Optimization

1. Line reprojection error (for frame k)
- $d\left(\mathbf{p}, \mathbf{l} \right)$: distance of point **p** to line **l**
- ${ }^k \mathbf{\bar{l}}_i$: 2D observation of 3D line $\mathbf{L}_i$ on frame k
- ${ }^k \mathbf{l}_i$: 2D reprojection of $\mathbf{L}_i$ onto frame k
- ${ }^k \mathbf{\bar{p}}_{i, 1}, { }^k \mathbf{\bar{p}}_{i, 2}$: 2 (2D) endpoints of ${ }^k \mathbf{\bar{l}}_i$

$$
e_l\left({ }^k \mathbf{\bar{l}}_i, { }^k \mathbf{l}_i\right) = \begin{bmatrix}
d\left({ }^k \mathbf{\bar{p}}_{i, 1}, { }^k \mathbf{l}_i\right) & d\left({ }^k \mathbf{\bar{p}}_{i, 2}, { }^k \mathbf{l}_i\right)
\end{bmatrix}^T \in \mathbb{R}^2
$$

2. Point reprojection error (frame k)
- ${ }_w^c \mathbf{R}, { }_w^c \mathbf{t}$: rotation matrix & transformation vector from world to camera frame
- ${ }^w \mathbf{X}_q$: 3D map point
- $\mathbf{\bar{x}}_q$: 2D observation on frame k

$$
\mathbf{E}_{p_{k, q}}={ }^k \mathbf{\bar{x}}_q-\pi\left({ }_w^c \mathbf{R}\ { }^w \mathbf{X}_q+{ }_w^c \mathbf{t}\right),
$$

<figure>


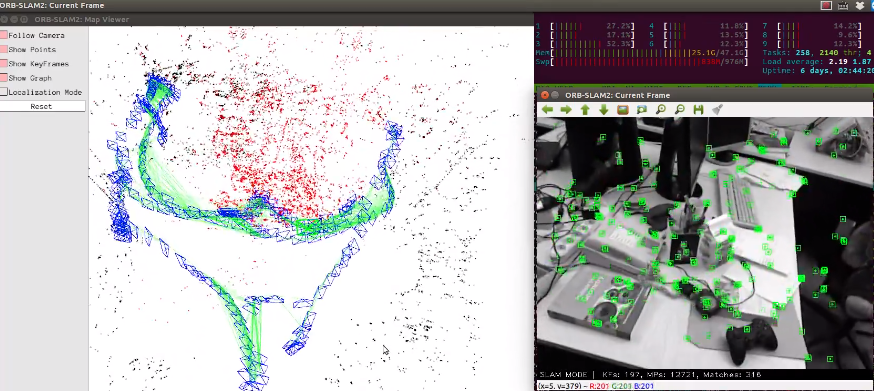
<figcaption>

ORB-SLAM2 GUI. To show the concept of keyframes & map points & co-visibility graph.
Blue rectangles are keyframe, points are 3D map points.
Cameras can view as nodes, edges (if #co-visible points between keyframe > threshold can form an edge) can form a co-visibility graph.

</figcaption></figure>

# Experiments

- All SLAM systems used to compare are disabled loop closure & re-localization part for fair comparison to VO systems
- **Datasets**:
1. OIVIO: <abbr title="Visual-Inertial">VI</abbr> data that a robot in tunnels with onboard illumination
2. UMA-VI: illumination-challenging scene with handheld sensors
- **Metrics**: RMSE translational error

## Results on OIVIO Benchmark

- Observed that features like LSSD, KLT sparse optical flow, ZNCC, LBD line descriptor are not robust in dynamic environments
- KLT: VINS-Fusion
- ZNCC: StructVIO
- LBD: UV-SLAM

<figure>


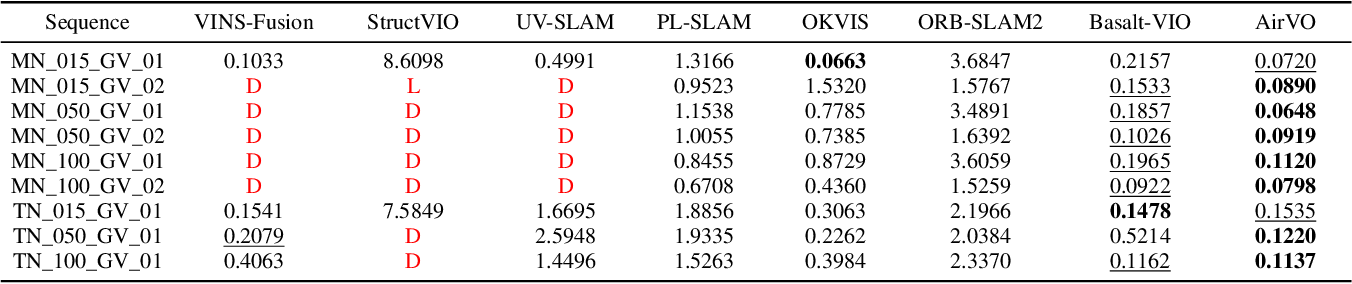
<figcaption>

<span style="color: red;">D</span> = error > 10m

</figcaption></figure><figure>


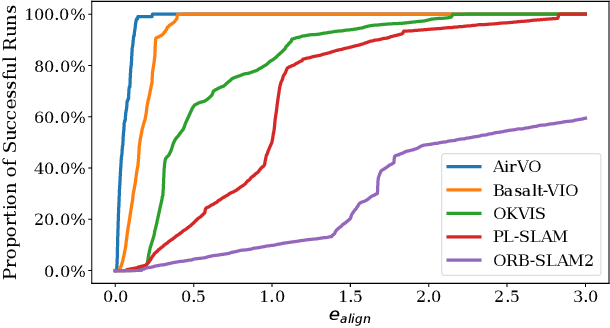
<figcaption>

On OIVIO MN\_050\_GV_01. If alignment error < $e_{align}$ is treated as fail

</figcaption></figure>

## Results on UMA-VI Benchmark

- Only illumination robust methods are shown

<figure>


<figcaption>

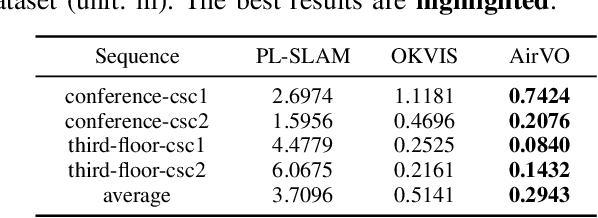
Results on UMA-VI dataset. PL-SLAM use LBD line descriptor to match lines

</figcaption></figure><figure>


<figcaption>

Samples of UMA-VI dataset. Turning on/off light that result in dynamic illumination

</figcaption></figure><figure>


<figcaption>

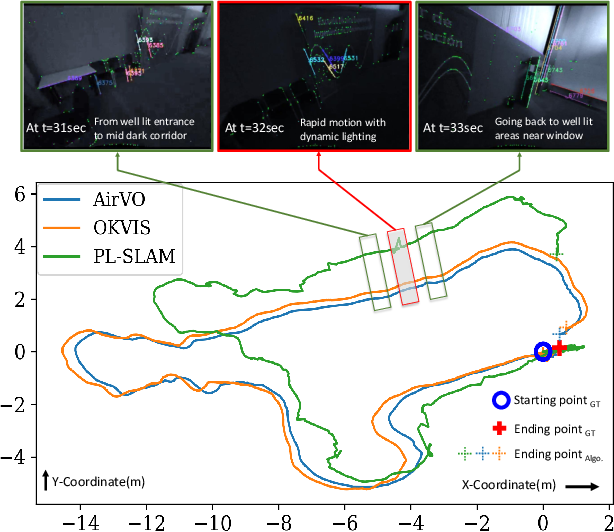
On UMA-VI conference-csc2 sequence.

</figcaption></figure>

## Ablation Study

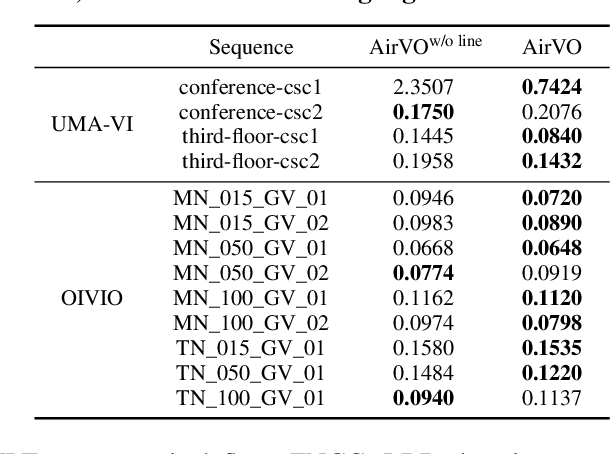
- W/ line features $\downarrow$ 45.6% translational error average


## Runtime Analysis

- Nvidia Jetson AGX Xavier (2018):
- CPU: 8-core ARM v8.2 64-bit
- GPU: 512-core NVIDIA Volta
- All algorithm:
- Input image: 640 $\times$ 480
- Extract 200 keypoints
- Disable loop closure, re-localization & visualization

<figure>


<figcaption>

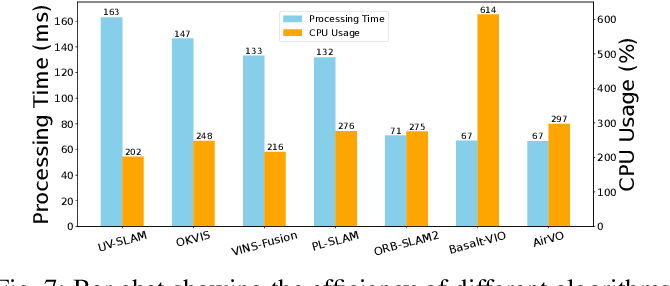
CPU usage & per-frame processing time on Nvidia Jetson AGX Xavier (2018)

</figcaption></figure><figure>


<figcaption>

Running time comparison of each module. PE = point extraction, LE = line extraction, PM = point matching, LM = line matching, IPE = initial pose estimation & BA = bundle adjustment

</figcaption></figure>

# Conclusion/Future works

1. \+ loop closure, re-localization

**Found improvements**

2. Tracking only use monocular image, not utilize the whole stereo input
- Not use stereo's fixed extrinsic info.
- To reduce computation?
3. Employ direct method but weight more NN extracted features to get robust & dense map

## Optimizations for edge device

- FP16 NNs run on GPU
- Multi-treading utilizes both CPU & GPU
- Back-end triggered only after keyframe created
- Using Point-line association to match line
- Prevent extract descriptor & still illuminance robust

* * *

1. VON GIOI, Rafael Grompone, et al. LSD: A line segment detector. Image Processing On Line, 2012, 2: 35-55. [↩︎](#fnref1)