# 2025 ICG Midterm Scoring criteria

## 1(a) 12pt

Description(2pt) & formula(2pt) each

1. Ambient (4pt)
- light sources come from the environment (1pt)
- light up the basic shape of the model (1pt)
- formula $I_a=K_aI_a$ (2pt)
2. Diffuse (4pt)
- for a microscopically **rough** surface, the iincoming light is **scattered equally in all directly**. (2pt)
- formula $I_d=K_d \space I_d \space(\vec{n} \cdot \vec{l})$ (2pt)
Reflected intensities vary with the direction of the light (the formula shows)
3. Specular (4pt)
- bright highlight where light is reflected **mainly** toward the mirror reflection direction. (2pt)
- reflection light is not that right.
- formula $I_s=K_s \space I_s \space (\vec{v} \cdot \vec{r})^\alpha$ (2pt)
- shininess $\alpha$ (-1pt if missing)
- A higher shininess exponent $n$ or $\alpha$ results in a smaller, sharper specular highlight, which is characteristic of a shinier surface. 
- Shininess Exponent $\alpha$: A higher value creates a tighter, sharper highlight, simulating a very smooth, **mirror-like** surface. A lower value creates a broader, softer highlight, simulating a **rougher surface**.

The specify the four vector with correct direction. (-1pt if missing. belong to the formula)

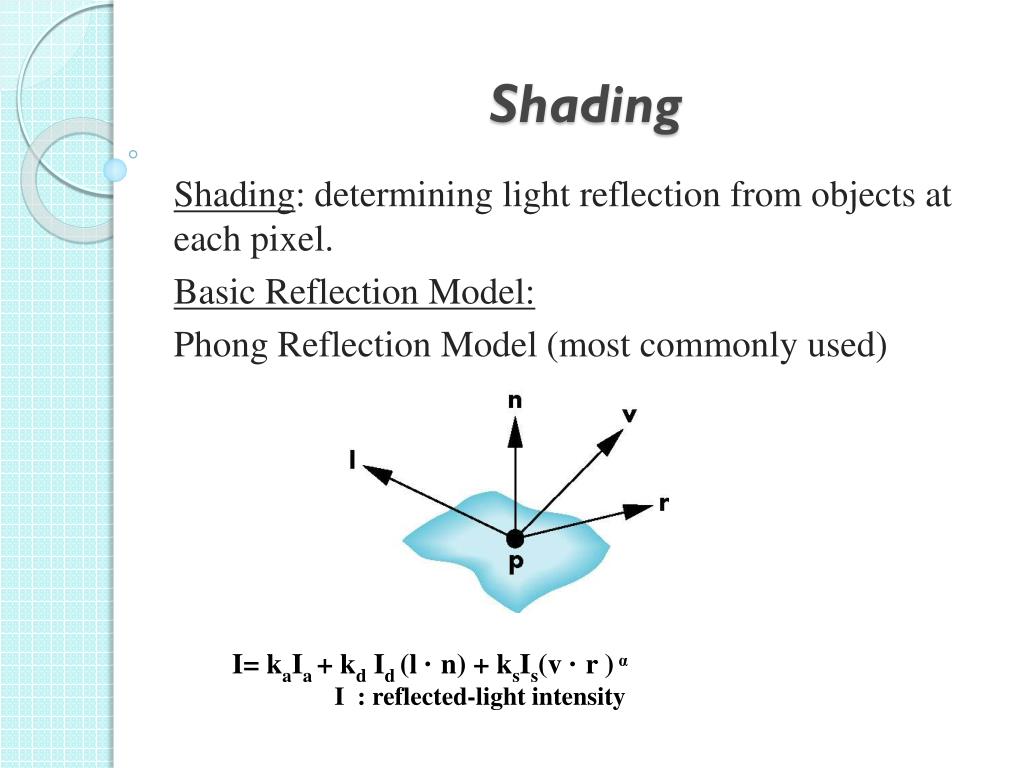
## 1(b) 6pt

1. Identify ==**MAIN contribution**== (1pt each)
2. Reasons (1pt each)



## 2

## 3(a) 5pt

No (3pt), with your reason. (2pt)

Fixed-function pipeline only can calculate Gourand shading. No GLSL/Programmable pipeline, **which means no vertex/gometry/fragment shader.**

## 3(b) 5pt

Fragment shader (3pt) + your reason (2pt)

Phong shading needs an accurate normal and view direction at each pixel to compute the small, sharp specular highlight, and only the **fragment shader** can do that **per-pixel**. (-1 pt if missing)

The **vertex shader** can only compute **per-vertex values**. If you calculate specular there, you end up with Gouraud shading, where the highlight gets smeared because it's interpolated across the surface. So true Phong shading works like this:

- The vertex shader passes down normals, positions, and other data (to be interpolated).
- The fragment shader uses the interpolated normal to compute $I$.

## 3\(c) 6pt

1. No (2 pt)
2. Explain how to get the points in shaders if answer yes. (-1pt)
3. Calculate normal with cross (2pt)
4. Specify the problem of using the pre-calculated method. (1pt)
- we average the surface normals to get the normal vector at Vectex V.
- if not, it would be like flat shading.
- phong shading normals
]
- gourand shading

## 4

## 5a (8pt)

u += 6; u %= 360;

Ans 1: $T(0, 0, -d) * Ry(-u) * T(0, 0, -r_B) * Ry(90);$

Ans 2: $T(r_B * sin(u), 0, r_B * (-cos(u)) - d) * Ry(90-u);$

1. comment 1pt
2. rotate center 2pt
3. rotate degree 1pt
4. rotate radius 2pt
5. turtle direction 2pt

## 5b (7pt)

v += 12; v %= 360; (or v -= 12)

Ans: $M_{tur} * T(0, e, 0) * R_z(v) * R_y(180);$

1. comment 1pt
2. local rotate center 1pt
3. local rotate degree 1pt
4. local rotate radius 1pt
5. fish direction 1pt
6. global system 2pt

In this part, we will assume your turtle model is correct.

## 5c (5pt)

Ans 1: $R_y(180) * R_z(-v) * T(0, -e, 0);$

Ans 2: $M_{fish}^{-1} * M_{tur} * P_{tur};$

1. comment 1pt
2. rotate degree 1pt
3. rotate center 1pt
4. fish direction 1pt
5. turtle model 1pt

If you have mentioned the transform model is the inverse of the **local** model of the fish or the inverse fish model multiplied by the turtle model, you will get the score of part 2, 3, 4 (3 pt).
If you have mentioned only inverse fish model, you will get only 2 pt for part 2, 3, 4.
In this part, we will assume your turtle model and mosquito model are correct.

## Score distribution


### average = 67.59