# 生成模型與潛在空間 (Generative Modelling in Latent Space)

> 原始論文：[Generative modelling in Latent Space](https://sander.ai/2025/04/15/latents.html) - 2025/4/15

---

## 引言與核心概念

### 現代生成模型的兩階段流程
1. **潛在表徵提取**：從輸入數據 (如圖像的像素) 中學習一個更低維度、更抽象的**潛在表徵 (Latent Representation)**。
2. **Latent Space 生成**：在這個緊湊的 Latent Space 中迭代訓練一個生成模型，然後可以從這個空間中採樣並通過 Decoder 映射回原始數據空間。

### 潛在表徵 (Latent Representation) 的定義與特性
潛在表徵在現代生成模型中無處不在。這裡所說的「Latents」 (潛在表徵) 通常指「latent representation」的簡稱。這個術語源於統計學中的潛在表徵概念，但在當前語境下其含義有所演變。這些潛在表徵並不代表任何我們無法直接測量的已知潛在物理量；相反，它們以緊湊的方式捕捉了感知上有意義的信息，並且在許多情況下，它們是輸入信號的確定性非線性函數 (即非隨機表徵)。

這些 Latents 具有幾個關鍵特性：
* **緊湊性**：維度遠低於原始數據，有效壓縮信息。
* **高層次性**：捕捉數據中的抽象特徵和語義信息，而非原始細節。
* **感知意義**：理想的潛在表徵應主要包含對人類感知重要的信息，過濾掉不相關的 noise 或細節。
* **確定性函數**：在許多現代應用中，潛在表徵是輸入的確定性非線性轉換結果，而非隨機表徵。

> 閱讀本筆記需具備神經網路、生成模型及相關概念的基礎知識。

---
## 方法學 (The Recipe)

在 Latent Space 中訓練生成模型的常規過程，可以劃分為以下兩個階段：

### 1. 訓練一個[自編碼器 (Auto-encoder)](https://hackmd.io/@Jaychao2099/imrobot9) 處理輸入信號
* Auto-encoder 是一個由兩個子網路組成的神經網路：編碼器 (Encoder) 和解碼器 (Decoder)。
* **編碼器 (Encoder)**：將輸入信號映射到其對應的潛在表徵 (編碼過程)。
* **解碼器 (Decoder)**：將潛在表徵映射回輸入域 (解碼過程)。
* 此階段的目標是學習 $(\nabla)$ 一個能夠有效壓縮輸入並能高保真度重建輸入的 Latent Space。
### 2. 在潛在表徵上訓練一個生成模型
* 使用第一階段訓練好的 Encoder 來提取訓練數據的 Latents。
* 然後，生成模型直接在這些 Latents 上進行訓練 $(\nabla)$。
* 目前，這類生成模型通常是 [自回歸模型 (Autoregressive Model)](https://hackmd.io/@Jaychao2099/imrobot6#Autoregressive-AT-Decoder) 或 [擴散模型 (Diffusion Model)](https://hackmd.io/@Jaychao2099/gen-ai-11#Diffusion-Model)。
* 一旦 AutoEncoder 在第一階段訓練完成，其參數在第二階段將不再改變：來自第二階段學習過程的梯度不會反向傳播到 Encoder。換言之，Encoder 的參數在第二階段是**凍結 (frozen ❄️)** 的。
* **採樣 (sampling)**：即從訓練好的生成模型生成新數據。
值得注意的是，AutoEncoder 的 Decoder 部分在第二階段的訓練中不起作用，但在從生成模型進行 **採樣** 時是必需的，因為生成模型會在 Latent Space 中生成輸出，需要 Decoder 將這些潛在輸出映射回原始輸入空間。

### 損失函數 (Loss Functions) 的角色
在兩個訓練階段中涉及到幾種不同的損失函數，它們 **確保模型學習到期望的特性**。下圖以紅色標註了這些損失函數在流程中的位置：

#### 角色一：確保 Encoder 和 Decoder 能夠高保真地轉換 input 與 Latents
幾種損失函數用於約束 **重建 (Decoder 的輸出)** 與 **輸入** 之間的一致性。通常包括：
* **簡單回歸損失 (Regression Loss, $L_{regression}$)**：
* [均方誤差 (Mean Squared Error, MSE)](https://hackmd.io/@Jaychao2099/imrobot3#%E5%9D%87%E6%96%B9%E8%AA%A4%E5%B7%AE-Mean-Squared-Error-MSE)
* 平均絕對誤差 (Mean Absolute Error, MAE)
* **感知損失 (Perceptual Loss, $L_{perceptual}$)**：
* **目標**：更好地保留高頻內容，而這些內容在很大程度上會被 Regression Loss 所忽略。
* **作法**：鼓勵重建結果在感知特徵上與輸入匹配。通常藉助 **預訓練網路 (❄️)** 提取特徵。
* [LPIPS](https://arxiv.org/abs/1801.03924) 是一個常用於圖像的選擇。
* **對抗損失 (Adversarial Loss, $L_{adversarial}$)**：
* **目標**：提高輸出的真實感。
* **作法**：使用一個與 AutoEncoder 共同訓練的**判別器網路 (Discriminator Network)**，如 [生成對抗網路 (Generative Adversarial Networks, GANs)](https://hackmd.io/@Jaychao2099/imrobot7) 中的做法：
* Discriminator 學習區分**真實輸入信號**和**重建信號**。
* AutoEncoder 則學習**欺騙 Discriminator**。
* 為了避免訓練初期的不穩定性，通常會在訓練開始一段時間後才啟用。

#### 角色二：約束 Latents 的容量
* **瓶頸損失 (Bottleneck Loss, $L_{bottleneck}$)**：通常會直接對 Latents 應用一個額外的損失函數，稱為**瓶頸損失**，因為 Latents 構成了AutoEncoder 網路中的一個瓶頸。

#### 角色三：第二階段生成模型的訓練
* **生成模型**使用其**自身的損失函數 ($L_{generator}$)** 進行訓練，該損失函數獨立於第一階段使用的損失。
* 對於 Autoregressive Model，通常是 Negative Log-Likelihood Loss (負對數似然損失，等價於 [交叉熵損失 (Cross-Entropy Loss)](https://hackmd.io/@Jaychao2099/imrobot3#%E4%BA%A4%E5%8F%89%E7%86%B5-Cross-entropy))。
* 對於 Diffusion Model，則是擴散損失 (Diffusion Loss)。

儘管這種通用的兩階段方法經常會根據具體的應用場景 (尤其是在聲音和影像生成領域) 進行調整和修改，但這裡總結的組成部分代表了該建模方法在大多數現代實際應用中最常見的核心元素。

---
## 我們如何走到這一步 (How we got here)
回顧生成模型的發展歷程，可以發現並非一開始就採用潛在空間的策略。
### 早期生成模型的挑戰
當今兩種主流的生成建模範式——自回歸 (Autoregression) 和擴散 (Diffusion)，最初都是應用於感知信號的「原始」表徵法。
* **像素接龍**：[PixelRNN](https://arxiv.org/abs/1601.06759), [PixelCNN](http://papers.nips.cc/paper/6527-conditional-image-generation-with-pixelcnn-decoders)
* **取樣點接龍**：[WaveNet](https://arxiv.org/abs/1609.03499) , [SampleRNN](https://arxiv.org/abs/1612.07837)
* **像素 Diffusion**
* **取樣點 Diffusion**：[WaveGrad](https://arxiv.org/abs/2009.00713), [DiffWave](https://arxiv.org/abs/2009.09761)

此策略很快面臨巨大挑戰，主要原因：
* **擴展性問題 - 感知信號主要由不可感知的 noise 組成**：信號的總信息內容中，只有**一小部分**實際影響我們的感知。
* **解決方向**：確保生成模型能有效利用其容量，專注於建模**感知相關的部分**，從而使用更小、更快、更便宜的模型而不犧牲感知品質。

### 發展一：潛在自回歸 (Latent Autoregression)

圖像的 Latent Autoregression 模型因 [VQ-VAE (Vector Quantised-Variational Autoencoder) 論文](https://arxiv.org/abs/1711.00937) 的提出而取得巨大飛躍。

* **核心思想**：通過在 Auto-encoder 中插入 **vector quantisation bottleneck layer (向量量化瓶頸層)** 來學習神經網路的離散表徵。
* **圖像處理**：卷積編碼器產生比輸入低 4 倍解析度的空間向量網格 (空間位置少 16 倍)，再由瓶頸層量化。
* **生成方式**：可使用 PixelCNN 風格的模型一次生成一個潛在向量，而非逐像素。

#### 潛在空間操作的優勢
* **減少採樣步驟**：顯著減少 Autoregression 採樣的需求。
* **避免浪費容量**：在 Latent Space 而非 pixel space測量 Negative Log-Likelihood 損失，有助於避免在不可感知的 noise 上浪費模型容量。這相當於一種**更側重感知相關信號內容的損失函數**。
* 當時，離散化的 Latents 尤其重要，因為 Autoregression 模型在處理離散輸入時表現更佳。

#### Latent Space 結構的利用：
* 現代潛在表徵通常保留了「類似於原始輸入」的網格結構，這種結構被用於**提高生成模型網路架構的效率** (如 CNN、recurrence 或 attention layers)。
* 允許現有的「基於像素的模型」非常容易適應。

#### 後續發展：
* **[VQ-VAE 2](https://arxiv.org/abs/1906.00446)**：解析度提升至 256x256，透過規模化及多層次潛在網格改善圖像品質。
* **[VQGAN](https://arxiv.org/abs/2012.09841)**：結合 [GAN](https://hackmd.io/@Jaychao2099/imrobot7) 的對抗學習機制與 VQ-VAE 架構。
* 解析度縮減因子大幅增加至 16 倍 (空間位置減少 256 倍)。
* 對抗損失鼓勵生成逼真的 Decoder 輸出，即使無法完全遵循原始輸入。
* **VQGAN 的影響**：成為核心技術，促成感知信號生成建模的快速進展。

VQGAN 的出現成為了一項核心技術，極大地促進了感知信號生成建模領域的快速進展。許多現今兩階段生成模型方法中的元素，如 Regression Loss、Perceptual Loss、Adversarial Loss 的組合，在 VQGAN 論文中就已經初見端倪。

值得一提的是，雖然離散表徵在早期扮演了關鍵角色，但近期的研究也表明，在 **連續空間中進行自回歸建模** 同樣能夠取得良好的效果。[[1]](https://arxiv.org/abs/2312.02116)[[2]](https://arxiv.org/abs/2406.11838)

### 發展二：潛在擴散 (Latent Diffusion)

隨著 Latent Autoregression 和 Diffusion Model 的發展，結合兩者成為自然趨勢 (約 2021 年下半年)。
> **代表作**：Rombach 等人的《[High-Resolution Image Synthesis with Latent Diffusion Models](https://arxiv.org/abs/2112.10752)》，重用 VQGAN 並將 Autoregression Transformer 替換為基於 UNet 的 Diffusion Model，構成 Stable Diffusion 基礎。

#### 主流化過程：
* **早期商業模型**：使用「解析度級聯 (resolution cascades)」，在像素空間生成低解析度圖像，再用上採樣 Diffusion Model 提升解析度 (如 [DALL-E 2](https://openai.com/index/dall-e-2/), [Imagen 2](https://deepmind.google/technologies/imagen-2/))。
* **轉向 Latent 方法**：Stable Diffusion 後，多數模型轉向基於 Latent Space 的方法 (如 [DALL-E 3](https://openai.com/index/dall-e-3/), [Imagen 3](https://deepmind.google/technologies/imagen-3/))。

#### 與 Autoregression 模型的損失函數差異：
* **Autoregression**：通常為最大化 Likelihood。
* **Diffusion**：所有 noise 水平下的期望值，其中不同 noise 水平的相對權重，會影響模型學習到的內容。
> 可將典型 Diffusion Loss 解釋為一種**感知損失函數**，更強調感知上顯著的信號。

#### 兩階段方法的互補性：
儘管 Diffusion Loss 本身關注感知，但兩階段方法依然有其價值。主要基於兩點考慮：

1. **不同尺度下的感知差異**：尤其在視覺領域中，紋理和細節的建模具有其獨特性，可能需要與宏觀結構分開處理。對於這類細節，「對抗性」方法可能更適合。
2. **計算效率**：在緊湊的 Latent Space 操作，可避免處理龐大輸入，減少記憶體需求，加速訓練和採樣過程。

#### 端到端方法的嘗試：

雖然早期也有結合學習 Latents 和 Diffusion Prior 的研究 [[1]](https://arxiv.org/abs/2106.05931)[[2]](https://arxiv.org/abs/2106.15671)，但未普及。不過因為感知和計算效率上的雙重優勢，使得兩階段方法仍然是值得深入研究和應用的主流範式。

---
## 為何採用兩階段？ (Why two stages?)

### 核心動機：提升效率與成本效益
通過提取更緊湊、專注於感知相關部分的表徵，並對此表徵進行建模，使規模適中的生成模型能發揮超常性能。
> **與有損壓縮的類比**：核心思想相似。感知信號中的大部分信息位元不影響感知，類似 JPEG、MP3 利用信號冗餘及人類感官對不同頻率敏感度差異進行壓縮。

### 為何不用現有壓縮技術作為基礎？
* **機器學習的潛力驅使**：研究者通常傾向於嘗試用更多機器學習方法看是否能超越「手工製作」的算法，發掘出更優的表徵方式。
* **生成建模的額外約束**：用於生成建模的潛在表徵，除了要能有效壓縮信息外，還需要滿足一些額外的條件：
* **可模型性 (modelability)**：某些 Latents 比其他 Latents 更容易建模。一個理想的潛在空間應該具有良好的結構，使得生成模型能夠有效地捕捉其分佈規律。
* **結構保留**：Latents 中需保留一些結構，以便生成模型利用 [歸納偏置 (inductive biases)](https://zh.wikipedia.org/zh-tw/%E5%BD%92%E7%BA%B3%E5%81%8F%E7%BD%AE) 來提高學習效率和生成品質。例如，圖像的空間結構、音訊的時序結構等。
> **歸納偏置**：當資料不足時，人類預設某些規則或假設，期望幫助模型做出合理推論。

這就引出了一個在重建品質與潛在表徵的可模型性之間的權衡。過度壓縮可能會損失過多結構信息，使得潛在表徵難以被建模。

### 利用感知在不同尺度運作的差異：
* **聲音**：快速振幅變化感知為音高 (pitch)，慢速變化感知為節奏 (如鼓點)。
* **視覺**：顏色和強度的快速局部波動被感知為紋理 (textures)。
* **紋理 (texture/stuff) vs. 結構 (structure/things)**：
* 紋理 (如草地)：是高熵的 (high-entropy)，但人腦對其具體實現的細微差異不敏感。
* 結構 (如狗眼、天空)：細微差異則易被察覺。

好的 Latents 學習演算法，會對 texture 進行抽象，但同時保留清晰的 structure。重建的 texture 可與原始不同而不影響保真度，使 Auto-encoder 能 **更緊湊地** 表示 texture 的存在。

相對應的，生成模型也可以簡化，**只對 texture 的存在與否進行建模**，而無需浪費容量去捕獲 texture 的所有高熵細節。

### 接受額外複雜性的原因：
* 兩階段方法帶來 **顯著效率提升**，導致更快、更便宜的訓練，並極大加速採樣。
* 對於迭代優化的生成模型，這種 **成本降低** 的效益是非常重要的。

---
## 重建品質 與 可模型性 之間的權衡 (Trading off reconstruction quality and modelability)

在討論 Latents Learning 時，常常會將其與 **有損壓縮算法** 進行比較。大多數有損壓縮算法植根於 **[率失真理論 (Rate-Distortion Theory)](https://en.wikipedia.org/wiki/Rate%E2%80%93distortion_theory)**，該理論旨在量化 **壓縮程度** 與 **允許的失真度** 之間的關係。
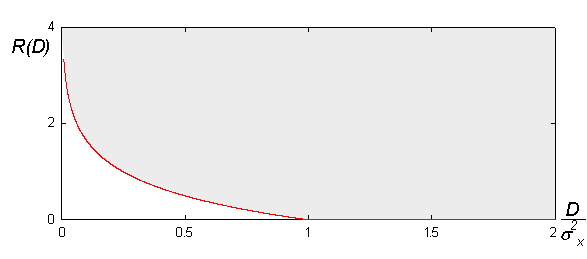
然而，當我們將 Latents 用於生成建模時，還需要引入第三個關鍵因素：**可模型性 (Modelability / Learnability)**。可模型性指的是生成模型 **捕捉 Latents 分佈的難易程度**。因此，我們實際上是在進行一個三向權衡，即 **rate-distortion-modelability 權衡**。

### Modelability 與 Distortion 的矛盾來源：
* 根源在於兩者對信號結構的不同處理方式：
* **有損壓縮**：利用已知信號結構減少冗餘，過程中常移除這些結構 (因解壓縮算法能重建)。
* **生成模型**：廣泛利用輸入信號的結構。
> 例如：透過架構性的歸納偏置，利用像 平移等變性 或 頻率頻譜 等信號特性。
* **衝突**：若算法移除幾乎所有冗餘，會使生成模型難以捕獲剩餘的非結構化可變性。
* **平衡點**：好的 Latents 學習算法會 **移除部分冗餘**，但 **保留足夠的信號結構** 供生成模型利用。

### 反面教材：熵編碼 (Entropy Coding)
一種無損壓縮方法，通過為 **頻繁出現的模式** 分配 **較短的 Latents** 來減少冗餘。(類似 Huffman coding)
* **問題**：不移除信息，但往往會**徹底破壞原始信號的結構**。輸入的微小變化可能導致壓縮信號的巨大變化，使建模極其困難。

### Latents 的特性：保留信號的宏觀結構
* **視覺例子**：Stable Diffusion 的 Latents 在視覺上仍能識別出物體，像帶雜訊 、低解析度、顏色失真的圖像。表明 encoder 幾乎未改變信號結構。
* **「高級像素 (advanced pixels)」概念**：捕捉了比原始像素多一點的少量額外信息，但主要行為仍像像素。

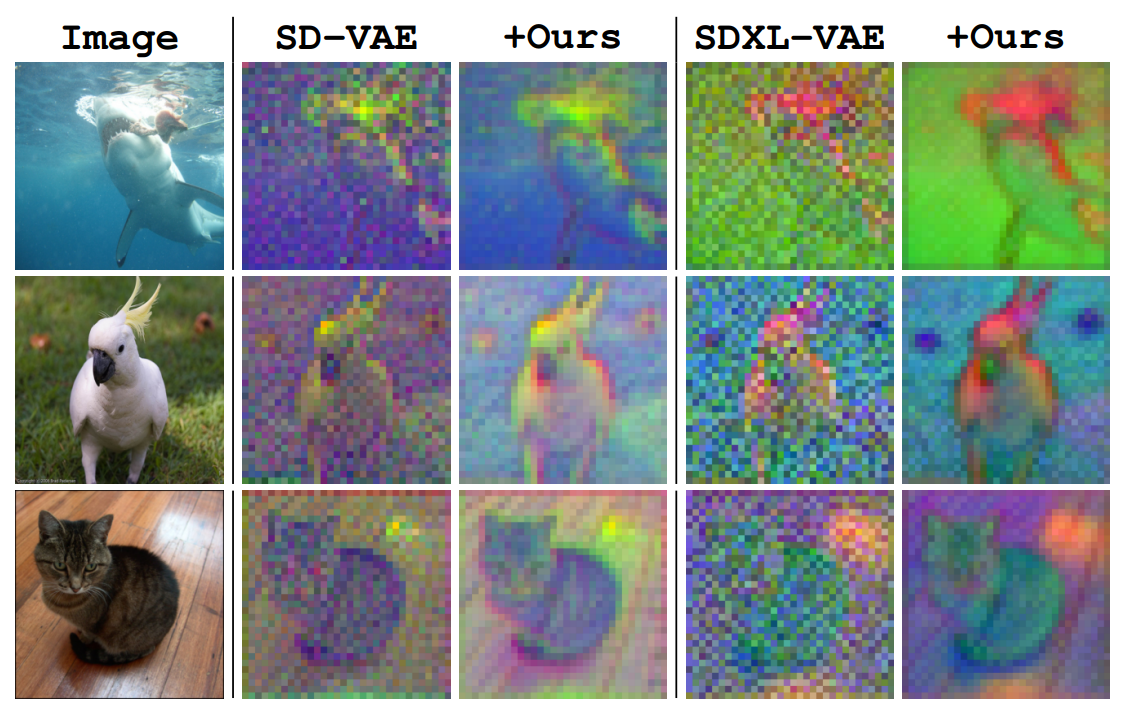
這種 **現代 Latents 的低階特性** 與傳統 VAE 將整個圖像壓縮為單一高階語義特徵向量不同。**現代用於生成建模的 Latents 更接近像素級別，容量更高**，通常會繼承輸入的網格結構 (儘管解析度會降低)。每個 Latents 向量可能抽象掉低階特徵 (如局部紋理 texture)，但並不直接捕獲整個圖像內容的全局語義信息。

因此，多數 Auto-encoder 不使用額外的條件信號 (如 Classification Tags)，因其主要約束高階結構，而潛在表徵本身更關注局部和中層的模式。

---
## 控制容量 (Controlling capacity)
對於具有網格結構 (grid structure) 的潛在空間而言，其 **容量 (capacity)** 的控制主要涉及到以下幾個關鍵的設計參數：
1. **降採樣因子 (Downsampling Factor)**：決定了 Latents 在空間維度上相對於原始輸入的 **縮小程度**。
2. **通道數 (Number of Channels)**：每個 Latents vector 所包含的 **分量數量**。
3. **碼本大小 (Codebook Size)** (若為離散表徵，例如 VQ-VAE 中的 code book)：對信息 **位元數** 施加硬性限制。

### 示例：
* **例子**：$256 \times 256 \times 3$ (RGB) 輸入圖像 $\rightarrow$ Encoder $\rightarrow 32 \times 32 \times 8$ 通道連續 Latent 向量網格。
* 空間上 Latent 向量比像素少 64 倍。
* 但每個 Latent 向量有 8 分量，像素只有 3 分量。
* **張量大小縮減因子 (TSR, Tensor Size Reduction Factor)**：Latents 張量與原始圖像張量分量數量的比率。(縮減了多少倍)
$$ \text{TSR} = \frac{W_{in} \cdot h_{in} \cdot C_{in}}{W_{out} \cdot h_{out} \cdot C_{out}} = \frac{256 \cdot 256 \cdot 3}{32 \cdot 32 \cdot 8} = 24 \text{ 倍} $$
* **TSR 的影響**：
* **若有相同 TSR，但不同配置**：若 Downsampling Factor 加倍 (網格 $16 \times 16$)，同時 Channels 增至 32，可保持 TSR 不變。**通常在重建品質上表現相似**。
* **若改變 TSR**：若改變 Downsampling Factor 而不改變 channels (反之亦然)，通常對**重建品質和可模型性均有深遠影響**。

### 單個數字信息容量的理論與實際限制：
從理論上講，**單個實值數字的信息容量是無限的**，如 [Tupper 自指公式](https://en.wikipedia.org/wiki/Tupper%27s_self-referential_formula)、無理數的無限不循環小數。

然而，在實際的機器學習應用中，有幾個因素限制了這種理論上的無限容量：
1. **有限精度浮點表徵**：例如 32 位單精度浮點數最多傳達 32 位信息。
2. **編碼器引入的 noise**：進一步限制有效精度，低位數字可能被 noise 淹沒。
3. **神經網路學習高度非線性函數的能力有限**：
* 神經網路自然偏向學習相對簡單、平滑的函數，這有助於其泛化。
* 將大量信息壓縮到少數數字中，需要高度非線性的映射函數，但高度非線性的映射往往會模糊信號結構，不利於 Modelability。
:::success
因此，具有 **更多分量** (Channels 更多，或維度更大) **的 Latents** 通常是更好的權衡。
:::

### 離散 Latents 的容量：
離散化對信息內容，容易受到碼本大小的硬性限制。
> 例如，一個擁有 512 個碼向量的碼本，每個潛在編碼最多能表示 $\log_2(512) = 9$ 位元的信息。

這些容量能否被有效利用，還取決於 encoder 的表達能力以及量化策略的有效性（例如，碼本是否被充分利用）。

### 選擇正確 TSR 的重要性：
因此，**選擇正確的 TSR (或者說，選擇合適的潛在空間維度和通道數組合)** 至關重要。這其中存在一個微妙的權衡：
* **權衡**：
* **較大的 Latents (較低的 TSR)**：重建品質更好 (高率，低失真)，但可能對可模型性產生負面影響 (需要更大容量的生成模型)。
* **較小的潛在表徵 (即較高的 TSR)**：更容易被建模，但可能會犧牲重建品質。

通常最佳的 TSR 和潛在空間配置是 **通過經驗性地調整和實驗來確定的**。這是因為目前尚缺乏可靠且計算成本低廉的代理指標 (proxy metrics) 來直接衡量 Latents 的 Modelability。往往需要實際訓練足夠多個生成模型，並評估其生成效果，才能判斷 Latents 的優劣。

### 當前趨勢：
:::success
**增加空間 Downsampling Factor (即更小的 Latents)**，並相應增加通道數以 **保持 TSR**，以便於在更高解析度下生成圖像和影像。
:::

---
## 整理與塑造 Latent Space (Curating and shaping the Latent Space)

僅僅控制 Latents 包含多少信息是不夠的。為了學習到一個優良的潛在空間，還需要精確地控制以下兩個方面：
* **整理 (Curating)**：決定應 **保留** 原始輸入信號中的 **哪些特定位元** (特徵)。
* **塑造 (Shaping)**：決定這些被保留下來的信息是如何在潛在空間中 **組織和呈現**。(涉及到 Latents 的分佈特性、尺度、之間的相關性等)

這個區分可能有些微妙，但卻非常重要。通常會採用各種 **正則化策略 (regularisation strategies)** 來實現對潛在空間的整理、塑造以及容量控制。本節將主要關注連續潛在表徵的情況。

### 策略一：VQGAN 與 KL-regularised Latents
Rombach 等人提出的[連續 Latent Space 正則化策略](https://arxiv.org/abs/2112.10752)：
1. **VQ-reg**：遵循 VQGAN 方法，將 **量化步驟重新解釋為 Decoder 的一部分**，以獲得一個連續的表徵 (量化前的向量)。
* **優點**：對 Autoregression 模型效果好，訓練時量化可防止 Latents 編碼過多細節信息。
* **限制**：在許多情況下，encoder 的表達能力本身往往是限制 Latents 信息量的主要因素。因此，這種額外的保障措施 (通過模擬量化) 可能並非總是必需的。
2. **KL-reg**：移除顯式的量化步驟，引入 **KL 散度懲罰項** (類似傳統 VAE)。
* **KL 正則化**：傳統 VAE 的核心，構成了證據下界 (ELBO) 的一項，旨在鼓勵 Latents 的分佈逼近一個預設的先驗分佈 (通常是標準高斯分佈)。
* **關鍵問題**：嚴格來說，ELBO 僅在 KL 項前面 **沒有縮放超參數 (=1)** 時，才真正是 Likelihood 的下界。
* **現代實踐**：幾乎總是將 KL 項的權重 **顯著縮小** (幾個數量級)，使其與原始的變分推斷背景 ([variational inference](https://zh.wikipedia.org/wiki/%E5%8F%98%E5%88%86%E8%B4%9D%E5%8F%B6%E6%96%AF%E6%96%B9%E6%B3%95) context) 的聯繫減至極弱。

#### 為何要縮小 KL 項的權重呢？
* **主要原因**：未縮放的 KL 項影響過強，嚴格限制 Latent 容量，嚴重降低重建品質。Latents 被迫過於接近簡單的高斯分佈，難以有效編碼輸入數據的複雜信息。
> 值得一提的是，在某些更關心**語義可解釋性**和**解纏結性**的場景，增加 KL 項尺度可能有效，如 [beta-VAE](https://openreview.net/forum?id=Sy2fzU9gl)。

#### 在 VAE 中的「V」：
* **KL 項的實際主要作用**：在一定程度上抑制潛在空間中的異常值，並約束 Latents 的尺度。

原文作者認為，這個「V」在很大程度上已經失去了其最初的統計學意義，主要是歷史性的。不如直接稱為 「KL 正則化的 autoencoder」。

總之，KL 項常被描述為約束 Latents 容量的手段，但在實際應用中主要用來約束 Latents 的 **形狀 (shape)** ，且效果相對溫和。

### 策略二：調整重建損失 (Tweaking reconstruction losses)
**重建損失函數** (regression, perceptual and adversarial)[↩](####角色一：確保-Encoder-和-Decoder-能夠高保真地轉換-input-與-Latents) 不僅僅是為了最大化解碼信號的品質，它在**整理 (curating) Latents** 方面也扮演著至關重要的角色，即決定了 encoder 應該將哪些類型的信息編碼到潛在空間中。

#### 思想實驗：
* **實驗**：僅保留回歸損失 (Regression Loss, $L_{regression}$)，如傳統 VAE。
* **結果**：傾向於產生**模糊的重建結果**。
* **原因**：簡單的 Regression Loss (如 L2 損失) 對於所有類型的信號內容一視同仁，它會 **不成比例地專注於優化低頻內容 ，因低頻分量 (structure...) 在自然圖像中佔比較大**。高頻內容 (texture, edge...) 的感知重要性遠大於其信號功率佔比，但被 Regression Loss 忽略。[↩](###利用感知在不同尺度運作的差異：)
> VQGAN 與僅使用 Regression Loss 訓練的 DALL-E VAE 進行比較，顯示了 Perceptual Loss 和 Adversarial Loss 的影響。

#### 那能否完全去掉回歸損失？
* **答案**：通常不是好主意。
* **原因**：Perceptual Loss和 Adversarial Loss 更難優化，易陷入局部最小值 (尤其是依賴於預訓練的、固定的特徵提取網路時)。在這種情況下，Regression Loss 可以充當一種 **正則化器 (regulariser)**，為訓練過程提供一個相對平滑和穩定的梯度引導方向，有助於模型收斂到一個較好的解。

#### 不同重建損失策略的例子：
1. **[DCAE](https://arxiv.org/abs/2207.04491)**：在音訊解碼中，將 L2 回歸損失 (MSE) 替換為 L1 (MAE)，保留 LPIPS Perceptual Loss [↩](####角色一：確保-Encoder-和-Decoder-能夠高保真地轉換-input-與-Latents) 和基於 [PatchGAN](https://arxiv.org/abs/1611.07004) 的判別器。多階段訓練，Adversarial Loss 僅在最後階段啟用。
2. **[VIT-VQGAN](https://arxiv.org/abs/2110.04627)**：結合 L2 損失和 [logit-Laplace 損失](https://arxiv.org/abs/2102.12092) (皆可視為 Regression Loss)，並使用類似 [StyleGAN](https://arxiv.org/abs/1912.04958) 的判別器及 LPIPS Perceptual Loss。
3. **[LTX-Video](https://arxiv.org/abs/2402.14413)**：引入基於離散小波變換 (DWT) 的影像 Perceptual Loss，使用改進的對抗損失策略 (reconstruction-GAN)。

可以看出，就像烹飪一樣，不同的研究者和應用場景可能會發展出各自獨特的「秘方」，通過精心調配不同的損失函數及其權重，以期達到最佳的 Latents 學習和生成效果。

### 策略三：表徵學習 vs. 重建 (Representation learning vs. reconstruction)

* **核心論點**：學習一個用於生成建模的良好且緊湊的 Latents，與學習將該 Latents 解碼回輸入空間，是**兩個獨立的任務**。
* **問題**：
* 現代 Auto-encoder 期望同時完成兩者。
* 雖然在實踐中效果尚可 (便利性)，但可能混淆任務，對一個任務最優的選擇對另一任務未必最優。

#### 原作者 [2019 觀點](https://arxiv.org/abs/1903.04933)：當 Decoder 是 Autoregression 時，混淆任務尤其有問題。
* **建議**：使用**單獨的非 Autoregression 輔助解碼器 (auxiliary decoder)** 為 encoder 提供學習信號。
* **主解碼器 (Primary Decoder)**：專注於 **最大化重建品質** (梯度 **不反向傳播** 到 encoder，不參與 Latents 的學習)。
* **輔助解碼器 (Auxiliary Decoder)**：負責 **塑造和整理 Latent Space** (梯度 **會反向傳播** 到 encoder，參與 Latents 的學習)。
* **優點**：仍可聯合訓練，因此額外複雜性有限。且 Auxiliary Decoder 訓練後可丟棄，不影響最終的生成過程。

#### Auxiliary Decoder 的現代意義：
即使 2019 論文中的像素空間 Autoregression Decoder 的想法有些過時，**使用 Auxiliary Decoder 分離 表徵學習 和 重建任務** 的核心思想，在當今的生成領域仍然具有非常現實的意義：
:::info
通過讓 Auxiliary Decoder 優化不同的損失函數，或採用不同的網路架構，或許能夠為編碼器提供更好的學習信號，提升整體生成模型的性能。
:::
* **其他研究者的共識**：Zhu 等人也得出 [類似結論](https://arxiv.org/abs/2410.12490)，使用 [DINOv2](https://arxiv.org/abs/2304.07193) 特徵上的 K-means 構建離散 Latents，並結合單獨訓練的 Decoder。
* **自監督學習表徵的重用**：在 **聲音模型** 中更為常見：將通過自監督學習預訓練好的表徵，直接用於下游任務，或作為 Latents 的一部分。可能因聲音領域的研究者們更習慣於訓練 **聲碼器 (vocoders)**，將預先定義好的中間表徵 (例如梅爾頻譜圖, mel spectrograms) 轉換回原始聲音波形。

### 策略四：為 modelability 進行正則化
* **影響 modelability 的因素**：
1. **容量約束**：決定 Latents 中的 **信息量**。容量越高，生成模型需越強大。
2. **塑造 (Shaping)**：相同信息可用 **不同方式表達**，有些更易建模。縮放程度、標準化程度、高階統計量 (如峰度、偏度) 和相關性結構，都對 modelability 有重要影響。
3. **整理 (Curation)**：某些 **信息類型** 比其他更易建模。若 Latents 編碼了輸入信號中不可預測的 noise ，會使其更難預測。

前面提到的KL 散度懲罰項 [↩](###VQGAN-與-KL-regularised-Latents)，儘管常被認為是用於使 Latent Space 高斯化或平滑化，但它在這方面的實際效果可能並不像許多人想像的那麼強大，尤其是在其權重被大幅縮小之後。

#### 提升 modelability 的方法：
1. **使用生成先驗 (Generative Priors)**：
* 與 Auto-encoder 共同訓練一個 (輕量級的) 潛在生成模型。
* 將生成損失反向傳播到 encoder，鼓勵 encoder 學習到更容易被該 Generative Priors 所建模的 Latents，使 Latents 易於建模 (如 [LARP](https://arxiv.org/abs/2410.21264), [CRT](https://arxiv.org/abs/2412.16326))。
* 需仔細調整各個損失的權重，因為 生成損失 與 重建損失 是矛盾的存在。
> 一個完全不包含任何信息的 Latents (例如全零向量) 是最容易被建模的，但其重建品質也最差。
2. **使用預訓練表徵進行監督**：
* 鼓勵 Latents 能預測一些已有的、通過其他方式獲得的的高品質表徵 (例如通過自監督學習得到的 DINOv2 特徵 [↩](####Auxiliary-Decoder-的現代意義：))。
* **例如**：[VA-VAE](https://arxiv.org/abs/2501.01423), [MAETok](https://arxiv.org/abs/2502.03444), [GigaTok](https://arxiv.org/abs/2504.08736)。
3. **鼓勵等變性 (Equivariance)**：
* **Equivariance**：當輸入信號發生某些特定變換 (例如圖像的縮放、旋轉、平移) 時，其對應的 Latents 也應當發生類似的、可預測的變換。
* **例如**：[AuraEquiVAE](https://huggingface.co/fal/AuraEquiVAE), [EQ-VAE](https://arxiv.org/abs/2502.09509), [AF-VAE](https://arxiv.org/abs/2503.09419)。
* Equivariance 正則化使 Latent 的頻譜特性更類似於像素空間輸入的的頻譜特性，提高可模型性。因為許多生成模型（如 CNN）的架構本身就利用了這種等變性。
* **共同目標**：以上策略都試圖以某種方式增加 Latents 的 **[$\mathcal{V}$-information](https://arxiv.org/abs/2002.10689)**。
> **$\mathcal{V}$-information**：在考量觀察者的計算能力限制下，衡量從輸入 X 預測目標 Y 時「實際可用的資訊量」；若只能使用簡單模型 (如線性探針) 則計算限制造成可用資訊降低。
> * **與[互相資訊 (mutual Information)](https://zh.wikipedia.org/zh-tw/%E4%BA%92%E4%BF%A1%E6%81%AF) 的差異**：傳統 mutual Information 僅看位元量，不考慮模型複雜度；$\mathcal{V}$-information 則同時考慮「資訊可提取難度」，簡單模型能直接解讀的訊息較容易取得。
> * **為何重要**：在生成式模型中，希望 Latents 既保留足夠資訊，又能讓後續推論採用低算力即可完成，藉此減少運算成本。
> * **與率–失真–實用性關聯** [↩](##重建品質-與-可模型性-之間的權衡-(Trading-off-reconstruction-quality-and-modelability))：$\mathcal{V}$-information 將「實用性」（usefulness）納入，確保壓縮後的表示，對下游任務仍具可用價值。
>
> 高 $\mathcal{V}$-information 表示 **即便運算資源有限，也能用簡單模型快速從潛在表示中抽取關鍵資訊**，有助提升生成式模型在推論階段的效率。

### 策略五：一路擴散到底 (Diffusion all the way down)
這是一個特殊的類別，指的是 **帶有 diffusion decoder 的 Auto-encoder**：
* **傳統 Decoder**：前饋神經網路，通過單次前向傳播直接輸出像素值。經常需要通過對抗訓練來提升生成品質。
* **diffusion Decoder**：將 diffusion 原理用於 Latents 的解碼任務 (同時也隱含地對 Latents 的分佈進行了建模)。

這種架構不僅會影響最終的重建品質，也會深刻影響 Auto-encoder 學習到的 Latents 的類型。代表性例子：[SWYCC](https://arxiv.org/abs/2409.02529), [$\epsilon$-VAE](https://arxiv.org/abs/2410.04081), [DiTo](https://arxiv.org/abs/2501.18593)。

#### 採用動機：
1. **更有原則的層次化生成建模**：理論上，將 diffusion 同時用於 Latent Space 建模 和 Latents 解碼，能提供更完善的模型。
2. **簡化訓練，提升穩健性**：可以僅用 MSE 損失進行訓練，避免了對抗訓練中常見的超參數調整困難和訓練不穩定等問題。
3. **提升輸出品質**：將 diffusion 迭代優化的原則，應用於解碼。

#### Diffusion Decoder 的顯著弱點：
* **計算成本高昂**：多步迭代，使延遲遠高於傳統的前饋式 Decoder。
* **與兩階段方法的初衷相悖**：採用兩階段方法的一個關鍵原因是 **避免在緩慢且昂貴「輸入空間」的迭代優化**，改為在緊湊的 Latent Space 中進行迭代生成，然後通過一次快速的前向傳播解碼回輸入空間。

#### 可能的緩解：
* **[擴散蒸餾 (Diffusion Distillation)](https://sander.ai/2024/02/28/paradox.html)**：在具有豐富條件信號 (即 Latents) 的情況下，此方法被證明有效，甚至可達單步採樣。
* **DALL-E 3 的 [一致性解碼器 (Consistency Decoder)](https://huggingface.co/openai/consistency-decoder)**：重用 Stable Diffusion 的 Latent Space，訓練新的基於 diffusion 的 Decoder，再 [蒸餾 (consistency distillation)](https://arxiv.org/abs/2303.01469) 至只需兩步採樣。實驗結果表明，**視覺保真度顯著提高**，但延遲仍高於原始的對抗式 Decoder。
<center><img src="https://sander.ai/images/consistency_decoder.jpg" alt="image" width="60%" /></center>
* **[Music2Latent](https://arxiv.org/abs/2408.06500)**：在音樂頻譜圖上操作，可將帶有 Consistency Decoder 的 Auto-encoder 進行端到端訓練，並能在單步採樣產生高保真輸出，其延遲與對抗式 Decoder 相當。
* **[FlowMo](https://www.arxiv.org/abs/2503.11056)**：帶有 diffusion decoder 的 Auto-encoder，引入額外的「訓練後階段」，鼓勵 **mode-seeking behaviour (尋模行為)**。比較：
* **對抗損失**：傾向於丟棄數據分佈中的某些模式 (modes)，專注於提升單個樣本的真實感，而非整體的多樣性。
* **基於 diffusion 的損失**：通常不丟棄模式，而是試圖覆蓋整個數據分佈。FlowMo 的兩階段訓練策略使它的 Diffusion Decoder 能一定程度上模仿 mode-seeking behaviour，但仍需大量採樣步驟，計算成本高。

#### 早期 Diffusion Auto-encoder 的焦點：
如 [Diff-AE](https://arxiv.org/abs/2111.15640), [DiffuseVAE](https://arxiv.org/abs/2201.00308)，更側重學習無拓撲結構的高階語義表徵 (類似舊式 VAE)，關注可控性和解纏結性，而非直接用於大規模的感知信號生成。
* **[DisCo-Diff](https://arxiv.org/abs/2407.03300)**：介於兩者之間，用一系列離散 Latents 來增強 Diffusion Model。這些離散 Latents 可用 autoregressive prior 建模。

#### 總結與展望：
* 若能消除對抗訓練的需求，無疑會簡化簡化流程，因此 Diffusion Auto-encoder 是個有趣且流行的研究方向。
* 但在延遲方面，要與對抗式 decoder 競爭，仍具挑戰性。原文作者認為，目前 diffusion decoder 尚未準備好完全取代後者。

---
## 網格的束縛 (The tyranny of the grid)

當今大多數感知模態（如視覺、聽覺）的數字表徵都具有 **網格結構 (grid structure)**。這種 grid structure 源於對底層物理信號進行 **均勻採樣** 和 **量化** 的過程。例如：
* 圖像 $\rightarrow$ 2D 像素網格
* 影像 $\rightarrow$ 3D 網格
* 聲音 $\rightarrow$ 1D 網格 (序列)

均勻採樣意味著相鄰網格位置間存在固定量子 (距離或時間) 單位。

### 感知信號的近似平穩性 (approximate stationarity)：

* **定義**：
* 在局部區域內是相似的。這一特性與均勻採樣相結合，使得 grid structure 的數據中蘊含了豐富的 **拓撲結構** 和 **統計規律**。
* **神經網路的利用**：
* 通過廣泛的權重共享、卷積、循環和注意力機制，實現對平移、形變等變換的不變性 (invariance) 或等變性 (equivariance)。

#### 益處：==是構建強大機器學習模型的關鍵原因之一。==
* **進一步推論**：在設計 Latent Space 時 **保留此結構是個好主意**。
**原因**：
* 我們已經擁有大量為處理 grid structure 數據而優化的強大神經網路架構 (如 CNN、Transformer) 案例。
* 若 Latents 本身也具有類似結構，那這些現成的強大網路架構就能更有效地對其進行處理和建模。
* **對 Auto-encoder 的好處**：
* 因 **信號的平穩性** 和 **只對局部信號結構進行學習**，可在較小輸入裁剪塊 (patches) 或片段 (segments) 上進行訓練。
* 若施加正確架構約束 (例如限制感受野)，**在小塊數據上訓練得到的模型，往往可以直接泛化到比訓練時更大的 grid 上**，大幅降低第一階段的訓練成本。

### 網格結構的代價：冗餘的不均勻分佈
感知信號通常是高度冗餘的，並且這種冗餘在不同區域分佈並不均勻。
* **例子**：圖像中狗頭區域 (高感知細節) vs. 純藍天區域 (低信息)。
* 若 Latents 繼承了輸入的 grid structure，Auto-encoder 會「用相同容量」來編碼這兩個「信息含量截然不同的」區域。
* 若 Latents 豐富到能捕獲狗頭所有細節，必然就會浪費大量容量來編碼天空。
* **結論**：保留 grid structure 是以 **Latents 的編碼效率為巨大代價的**，這就是所謂的 「網格的束縛 (Tyranny of the Grid)」。
* **網格的束縛 (Tyranny of the Grid)**：
* **角度一**：
* 已存在之處理 grid structure 數據的神經網路，能力已經高度發達和優化。
* 任何偏離這種結構的嘗試，都不可避免地增加複雜性，使建模、訓練更困難，也對硬體不友好，因此通常不願意輕易放棄 grid structure。
* **角度二**：
* 但就編碼效率而言，因視聽信號中感知的顯著信息 (非冗餘信息) 分佈不均，會造成相當多浪費。

### Transformer 架構的潛力：
Transformer 被設計為處理 **集合值數據 (set-valued data)**，輸入的附加拓撲結構 (序列順序、空間位置)，會通過位置編碼 (positional encodings) 表達。

這使得相對於傳統的卷積或循環架構，Transformer 更容易適應那些偏離常規 grid structure 的數據表示。原文作者曾[探索過](https://arxiv.org/abs/2103.06089)，利用這一特性來實現可變速率離散表徵的語音生成。

### 新方法
#### 近年「放寬 Latent Space 拓撲結構約束」的發展趨勢：
旨在提高編碼效率和建模靈活性：
1. **將 Latents 從二維網格轉為一維序列結構 (2D $\rightarrow$ 1D)**：
* **[TiTok](https://arxiv.org/abs/2406.07550), [FlowMo](https://www.arxiv.org/abs/2503.11056)**：探索從圖像學習 1D 序列結構 Latents。動機之一是希望能利用強大的LLMs 進行序列建模，來處理圖像的 Latents。
2. **自適應序列長度/從粗到細結構**：
* **[One-D-Piece](https://arxiv.org/abs/2501.10064), [FlexTok](https://arxiv.org/abs/2502.13967), [Semanticist](https://arxiv.org/abs/2503.08685)**：使用[嵌套丟棄機制 (nested dropout)](https://arxiv.org/abs/1402.0915)，在 Latents 的 1D 序列中，誘導出 **從粗到細的層次結構**。使序列長度能適應輸入圖像複雜度和重建細節需求，進行自適應調整。
* **[ElasticTok87](https://arxiv.org/abs/2410.08368), [ALIT88](https://arxiv.org/abs/2411.02393), [CAT](https://arxiv.org/abs/2501.03120)**：也探索了類似的自適應性思想，但仍保持 2D 網格結構，僅根據內容自適應地調整 Latents grid 的解析度。
3. **完全放棄網格：「詞袋 (Bags of Tokens)」模型**：
* **[TokenSet](https://arxiv.org/abs/2503.16425)**：使用產生「詞袋」ltents (一組無序的潛在詞元) 的 Auto-encoder。

#### 這些新方法的共同點 (除 CAT 外)：
* 學習的 Latent Space 在 **語義上比「高級像素 (advanced pixels)」[↩](###Latents-的特性：保留信號的宏觀結構) 更高級別**，可以被看作是介於「高級像素」與舊式 VAE 的 vector-valued Latents 之間的一種中間狀態。
* FlexTok 和 Semanticist 以一個傳統 2D 網格結構 encoder 所產生的低階 Latents 作為其 1D 序列 encoder 的輸入。
* TiTok 和 One-D-Piece 也利用現有的 2D 網格結構 Latent Space 作為多階段訓練的一部分。
* **[相關想法](https://arxiv.org/abs/2412.06774)**：重用語言域中的詞元 (text tokens) 作為圖像的高級 Latents，利用了預訓練語言模型的強大能力。

#### 離散設置的探索：
此外，在離散的設置下，也有研究在探索網格中常見的 token 模式，是否可以借鑑類似 **語言詞元化 (tokenization)** 的思想，合併成更大的、語義更豐富的子單元 (sub-units)。
* [DiscreTalk](https://arxiv.org/abs/2005.05525) 是語音領域的一個早期範例，它在 VQ token 之上使用了 [SentencePiece](https://arxiv.org/abs/1808.06226)。
* [BPE 圖像 Tokenizer](https://arxiv.org/abs/2410.02155) 是這一思路較新的實現，它在 VQGAN token 上使用了增強型的 [byte-pair encoding](http://www.pennelynn.com/Documents/CUJ/HTML/94HTML/19940045.HTM) 算法。

---
## 其他模態的 Latents (Latents for other modalities)

以上討論主要集中在 **視覺領域 (圖像生成)**。主要是因為 **圖像的 Latents 學習相對更為成熟**，圍繞兩階段 (先學習 Latents，再在 Latent Space 建模) 圖像生成的研究也更為廣泛，並且已經催生了許多實際的產品和應用。在視覺領域，已存在比較完善的感知損失函數研究基礎，以及多種多樣的判別器網路架構可供選擇。

接著，簡要地看一下 Latents 在其他感知模態以及語言模態中的應用情況。

### 影像 (Video)：
仍屬視覺領域，但引入時間維度，帶來新的挑戰。
* **簡單方法**：逐幀重用圖像 Latents 的學習方法。
* **問題**：可能導致 **短暫視覺幻象 (temporal artifacts**，例如閃爍現象)，並且無法有效利用影像中存在的大量 **時間冗餘**。
* **當前不足**：時空 Latents 的學習工具還遠未成熟。**如何解釋人類對於運動和時間變化的感知特性**，仍然是一個有待深入研究的問題 (儘管傳統的影像壓縮算法已經廣泛利用了[運動預測](https://zh.wikipedia.org/wiki/%E8%BF%90%E5%8A%A8%E9%A2%84%E6%B5%8B)等技術)。

### 聲音 (Audio)：
情況與影像類似：
* 雖然兩階段方法已被廣泛採用 [[1]](https://arxiv.org/abs/2107.03312)[[2]](https://arxiv.org/abs/2210.13438)[[3]](https://arxiv.org/abs/2306.06546)，但 **如何進行必要的修改使其適應聲音信號的特性**，似乎還沒有形成廣泛共識
* 更常見的是，重用 通過 self-supervised learning，在大量無標籤聲音數據上預訓練得到的 Latents。

### 語言 (Language)：
語言是一種非感知模態，那兩階段方法能否提升大型語言模型 (LLMs) 的效率呢？
**答案：不那麼直接**。原因：
* **語言的低可壓縮性**：本質上比感知信號難壓縮很多 (為了高效通信而演化出來的符號系統，本身的冗餘相對較少)。
* 數學家 C. E. Shannon [估計英語大約有 50% 冗餘](https://ieeexplore.ieee.org/abstract/document/6773024)。相比之下，圖像/聲音/影像等感知信號可以在壓縮 **幾個數量級** 後，仍然保持較小的感知失真；而語言則不行，對語言進行如此高程度的有損壓縮，幾乎必然造成細微差別或丟失重要語義信息。

#### 標記器 ([Tokenizer](https://huggingface.co/learn/llm-course/zh-TW/chapter2/4?fw=pt))：
目前大型語言模型中廣泛使用的 Tokenizer (例如 [BPE](http://www.pennelynn.com/Documents/CUJ/HTML/94HTML/19940045.HTM), [SentencePiece](https://arxiv.org/abs/1808.06226)）通常是 **近似無損的** (將文本轉換為模型可以處理的 tokens 序列，同時保留所有原始信息)。因此，它們產生的 tokens 通常不被視為傳統意義上的「Latents」。
> 值得一提的是，[Byte Latent Transformer](https://arxiv.org/abs/2412.09871) 將兩階段的思想應用於設計一種動態的 tokenisation 策略，可以看作是一種特例。

#### 有損高階表徵：

然而，語言中相對缺乏冗餘性這一點，並未阻止人們嘗試 **讓機器學習到有損的高階表徵的方法**。用於感知訊號的技術或許無法直接沿用，但已有數種其他用於學習句子或段落層級抽象表徵的方法被探索出來。[[1]](https://arxiv.org/abs/2203.11370)[[2]](https://arxiv.org/abs/2306.02531)[[3]](https://arxiv.org/abs/2412.08821)

---
## 端到端最終會勝出嗎？ (Will end-to-end win in the end?)

深度學習發展早期的一個重要敘事是：**用端到端學習 (end-to-end learning) 取代手工設計的特徵工程和多階段的處理流程**。
> * **End-to-end learning**：一種機器學習的解決問題思路。將一個複雜任務從最初的原始輸入直接映射到最終的輸出，而無需將問題分解成多個獨立的子模塊或階段 (例如特徵提取、模型訓練) 進行學習和優化。
> * **目標**：最大化整體性能，並簡化工程實現的複雜性。

在分類任務 (classification) 中 (如圖像分類、目標檢測、語音識別)，這一理念已經基本實現。

然而，一個頗具諷刺意味的現狀是：在當前的生成建模領域，尤其是在感知信號生成方面，**主流的範式卻是兩階段的方法，它並非完全的端到端學習**。

### 兩階段方法 vs. 端到端 的爭論
我們應該如何看待這一現狀呢？目前在實際產品中部署的大多數文本到圖像/影像/聲音的模型，都廣泛使用了中間的 Latents，這是否僅僅是一個暫時的過渡階段？
* **兩階段方法的問題**
* **兩階段的複雜性**：給系統帶來了顯著的額外複雜性。
* **端到端的優雅與協調**：更優雅，且有助於確保系統各部分能夠與單一個總體目標一致。
* **端到端的制約因素：在原始輸入空間進行迭代優化的成本**
* **緩慢且昂貴**，原文作者認為短期內難以從根本上改變，尤其隨著人類對生成信號品質、解析度、長度的要求不斷提升。
* 因此 Latent Space 方法 在 **訓練效率** 和 **採樣延遲** 方面的好處，讓人難以放棄。
* 目前尚無大規模有效的可行替代方案。
> 註：此觀點有爭議，部分研究者認為應轉向端到端，但原文作者認為為時過早。

### 未來發展

#### 何時能回到單階段生成模型？
> 單階段模型：直接在輸入空間進行生成
* **現有單階段方法的嘗試**：如 [simple diffusion](https://arxiv.org/abs/2301.11093)、[Ambient space Flow Transformers](https://arxiv.org/abs/2412.03791), [PixelFlow](https://arxiv.org/abs/2504.07963)，在高解析度下已經展現出一定的有效性，但它們的計算成本效益通常不如基於 Latent Space 的兩階段方法。
* **硬體發展的影響**：隨著計算硬體 (GPU、TPU) 的性能持續高速發展，可能在未來某個時間點後，輸入空間模型雖然效率相對低，但在成本效益上卻變得更能讓人接受，優於 Latent Space 模型引入的複雜性。
* **具體時間點的預測**：取決於哪種模態、硬體改進速度和研究進展，難以預測。

#### 對 Latents 需求的演變：
* **過去**：需要 Latents 確保生成模型 **專注於感知相關內容**，忽略視覺不顯著的熵。這是因為直接在輸入空間優化 Likelihood Loss 的模型在這方面表現不佳，它們傾向於過度關注細枝末節和 noise。
* **現在**：已逐漸弄清如何對 [Autoregression](https://arxiv.org/abs/2411.19722) 和 [Diffusion](https://arxiv.org/abs/2303.00848) Model 的 Likelihood 損失函數進行 **感知重加權 (perceptually re-weighting**，例如引入 Perceptual Loss 或調整 diffusion 過程中的 noise 調度等方式)。在一定程度上消除了對於輸入空間模型的發展阻礙。
* **計算效率優勢依然重要**：儘管如此，今日 Latent Space 模型在計算效率上的優勢，仍然一如既往地重要。

#### 第三種替代方案：解析度級聯 (Resolution Cascade)
* 無需顯式的 Latnets 學習，但仍將生成問題分為多個階段。例如，先生成一個低解析度的圖像，然後再通過若干個 upsampling models 逐步提升其解析度。
* 早期商業模型 (如 DALL-E 2 的部分組件) 曾採用，但現在已失寵。
* **失寵原因**：原文作者認為，因為不同階段之間的分工並不理想：upsampling models 負擔過重，容易在級聯的各階段積累錯誤，導致最終生成品質受限。

---
## 總結與核心要點 (Closing thoughts)

### 關鍵要點回顧：
1. **現代 Latents 的特性**：更像「**高級像素 (advanced pixels)**」，而非傳統 VAE 的高階語義表徵。通常保留了輸入數據的網格結構 (儘管解析度降低)，並在局部區域內對低階特徵 (如紋理) 進行抽象。
2. **兩階段的優勢**：可為各階段 **使用不同損失函數**，並通過 **避免輸入空間進行迭代採樣** 顯著提高計算效率。
3. **複雜性與效益的權衡**：Latents 增加複雜性，但計算效率的好處使其至少目前可接受。
4. **設計 Latent Space 的三要素**：
* 控制容量 (capacity, 包含多少信息) [↩](##控制容量-(Controlling-capacity))
* 整理 (curation, 保留哪些類型的信息)
* 形狀 (shape, 信息如何組織和呈現) [↩](##整理與塑造-Latent-Space-(Curating-and-shaping-the-Latent-Space))
6. **保留結構的重要性**：在 Latent Space 中保留拓撲結構 (如網格 grid) 和統計數據 (如近似平穩性 approximate stationarity)，對 modelability (可模型性) 很重要，即使有時效率稍差。[↩](##網格的束縛 (The-tyranny-of-the-grid))
7. **VAE 中的「V」**：現代兩階段模型中，第一階段的 Auto-encoder 實為 KL 正則化的 Auto-encoder，且通常正則化程度很低。[↩](###策略一：VQGAN-與-KL-regularised-Latents)
> V 可被戲稱為 vestigial (殘留物)?!
9. **重建損失組合的穩固性**：回歸損失 (regression loss)、感知損失 (perceptual loss) 和對抗損失 (adversarial loss) 的組合，已經被廣泛採用。
10. **表徵學習與重建的分離**：「學習好的 Latents」和「從 Latents 重建數據」是兩個獨立任務，耦合在單個 Auto-encoder 中同時進行雖然方便，但可能並非最優。探索 **將這兩個任務進一步解耦的策略** 是一個值得關注的方向。

### 作者的感慨與展望：

回顧幾年前，原文作者曾[預測](https://sander.ai/2020/09/01/typicality.html#right-level)表徵學習在生成建模領域將扮演越來越重要的角色。當時，表徵學習社區的主要焦點仍然集中在為判別式任務學習高階的語義表徵；而生成建模則是用於服務表徵學習 (例如作為一種 self-supervised learning 的手段) 更為常見。

或許可以說，VQGAN 的出現，以及其後續引發的一系列工作，真正鞏固了當前這種以 Latents 為核心的兩階段生成建模範式成為主流的道路。