---
tags: Lab_ICC_II
---
<center>
<h3>
Universidade de São Paulo (USP)<br>
Instituto de Ciências Matemáticas e de Computação (ICMC)<br>
</h3>
<h3>
Bacharelado de Ciências de Computação<br>
Disciplina: Laboratório de Introdução à Ciência da Computação II<br>
Professor: Leonardo Pereira<br><br>
Aluno: Guilherme Machado Rios (11222839)
</h3>
<h1>
Contagem de operações e tempo de execução
</h1>
</center>

## Introdução

Serão feitas as análises de dois algoritmos envolvendo um vetor de inteiros. O primeiro deles realiza a ***inversão da ordem*** dos elementos desse vetor. Já o segundo realiza a ordenação dos inteiros via um ***bubble sort***.

## Implementação e contagem de operações

Tomando ***a*** como atribuição operações aritméticas e atribuições e ***b*** como comparações e operações lógicas (&&, || e !).

Função ***array_reverse()***:

void array_reverse(Array *array) {
	int temp;
	int end = array->len - 1; //[2*a]

	for (int i = 0; i < end / 2; i++) { //[(a + b) + (n/2)*(2*a + b)]
		temp = array->nums[i]; // (n/2)*[a]
		array->nums[i] = array->nums[end - i]; // (n/2)*[2*a]
		array->nums[end - i] = temp; //(n/2)*[2*a]
	}
}

// f(n) = (n/2)*(2*a + b + a + 2*a + 2*a) + 2*a + a + b
// f(n) = n*(7*a + b)/2 + 3*a + b

// Sendo a = b = K, temos:
// f(n) = 8K/2 * n + 4K
/********************
 | f(n) = 4K*n + 4K |
 ********************/
 
// array_reverse() -> O(n)

Função ***bubble_sort***:

void bubble_sort(Array *array) {
	int aux_swap;
	for (int limit = array->len; limit > 1; limit--) { //[(a + b) + n*(2*a + b)]
		for (int i = 1; i < limit; i++) { //n*(a + b) + (n² - n)*[(2*a + b)]/2
			if (array->nums[i - 1] > array->nums[i]) { //(n² - n)*[a + b]/2
				aux_swap = array->nums[i]; //(n² - n)*[a]/2
				array->nums[i] = array->nums[i - 1]; //(n² - n)*[2*a]/2
				array->nums[i - 1] = aux_swap; //(n² - n)*[2*a]/2
			}
		}
	}
}

// f(n) = n²*(2*a + b + a + b + a + 2*a + 2*a)/2 + 
//+ n*(2*a + b + a + b) -
//- n*(2*a + b + a + b + a + 2*a + 2*a)/2 + a + b

// f(n) = n²*(8*a + 2*b) + n*(3*a + 2*b) - n*(8*a + 2*b) + a + b

// Sendo a = b = K, temos:
// f(n) = 10K*n² + 5K*n - 10*n + 2K
/*****************************
 | f(n) = 10K*n² - 5K*n + 2K |
 *****************************/
 
 // bubble_sort() -> O(n²)

## Análise final com tempo de execução

Gerando os arquivos ***reverse.dat*** e ***sort.dat*** via uma função ***main()***:

int main() {
	int range;
	clock_t start, end;

	start = clock();
	int amt_base = 5e5;
	FILE *frev = fopen("reverse.dat", "w");
	for (int i = 1; i <= 1024; i *= 2) {
		printf("reverse() com %d números\n", amt_base * i);

		range = amt_base * i * 2;
		Array *v = array_gen_rand(amt_base * i, range);

		fprintf(frev, "%d : ", amt_base * i);
		for (int i = 0; i < 100; i++) {
			clock_t start_rev = clock();
			array_reverse(v);
			clock_t end_rev = clock();

			fprintf(frev, "%lf ", (end_rev - start_rev) / (double)CLOCKS_PER_SEC);
		}
		fprintf(frev, "\n");

		free(v->nums);
		free(v);
	}
	fclose(frev);
	end = clock();
	printf("Tempo para análise da função que inverte um vetor: %.2lf minutos\n", (end - start) / (double)CLOCKS_PER_SEC / 60);

	start = clock();
	amt_base = 1e3;
	FILE *fsort = fopen("sort.dat", "w");
	for (int i = 1; i <= 256; i *= 2) {
		printf("bubble() com %d números\n", amt_base * i);

		range = amt_base * i * 2;
		Array *v = array_gen_rand(amt_base * i, range);

		fprintf(fsort, "%d : ", amt_base * i);
		for (int i = 0; i < 100; i++) {
			clock_t start_sort = clock();
			bubble_sort(v);
			clock_t end_sort = clock();

			fprintf(fsort, "%lf ", (end_sort - start_sort) / (double)CLOCKS_PER_SEC);
		}
		fprintf(fsort, "\n");

		free(v->nums);
		free(v);
	}
	fclose(fsort);
	end = clock();
	printf("Tempo para análise da função que ordena um vetor: %.2lf minutos\n", (end - start) / (double)CLOCKS_PER_SEC / 60);

	return 0;
}

Podemos processá-los gerando gráficos com o script em ***process_data.py***:

import matplotlib.pyplot as plt

reverse_file = open("data/reverse.dat", "r")
reverse_dots = {"xs": [0], "ys": [0]}
while True:
	line = reverse_file.readline()
	if len(line) == 0: break

	line = line.split(" : ")
	x = int(line[0])
	times = [float(x) for x in line[1].strip().split(' ')]
	y = sum(times)/len(times)

	reverse_dots["xs"].append(x)
	reverse_dots["ys"].append(y)

xs = reverse_dots["xs"]
ys = reverse_dots["ys"]

rev_fig = plt.figure()

plt.suptitle("array_reverse() - time x N")
plt.xlabel("Array lenth")
plt.ylabel("Time (s)")
plt.scatter(xs, ys, c='m')
plt.plot(xs, ys, 'm--')
rev_fig.savefig("reverse.png")

sort_file = open("data/sort.dat", "r")
sort_dots = {"xs": [0], "ys": [0]}
while True:
	line = sort_file.readline()
	if len(line) == 0: break

	line = line.split(" : ")
	x = int(line[0])
	times = [float(x) for x in line[1].strip().split(' ')]
	y = sum(times)/len(times)

	sort_dots["xs"].append(x)
	sort_dots["ys"].append(y)

xs = sort_dots["xs"]
ys = sort_dots["ys"]

sort_fig = plt.figure()

sort_fig.suptitle("bubble_sort() - time x N")
plt.xlabel("Array lenth")
plt.ylabel("Time (s)")
plt.scatter(xs, ys, c='m')
plt.plot(xs, ys, 'm--')
sort_fig.savefig("sort.png")

Com os gráficos à mão podemos confirmar o antes analisado na contagem de operações e no cálculo do O():

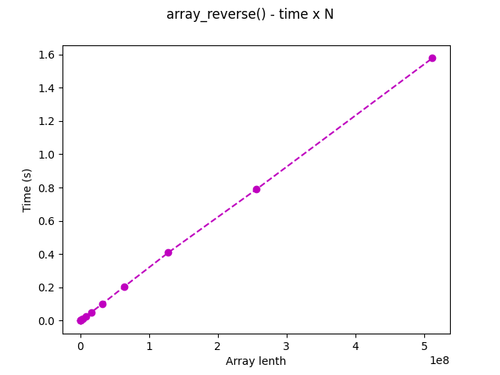[](reverse.png) [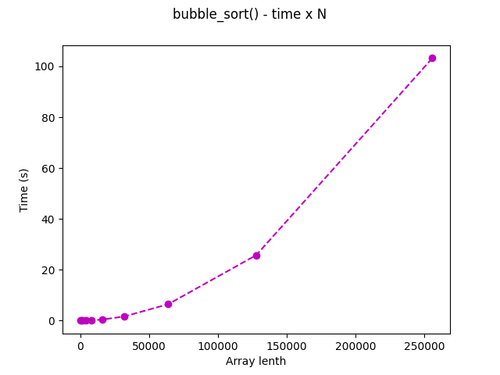](sort.png)

Vemos que o corportamento do tempo para a função de inverter vetor se comporta linearmente, enquanto para a função de ordenação o comportamento é exponencial.