# 北軟107 problemA

###### tags: `北軟107`

## 題目：
給你一個字串，請你列出字串中的字元的所有可能組合。

## 想法：
這題我們可以用遞迴，會比較直觀。
例如下圖即為遞迴樹狀圖。


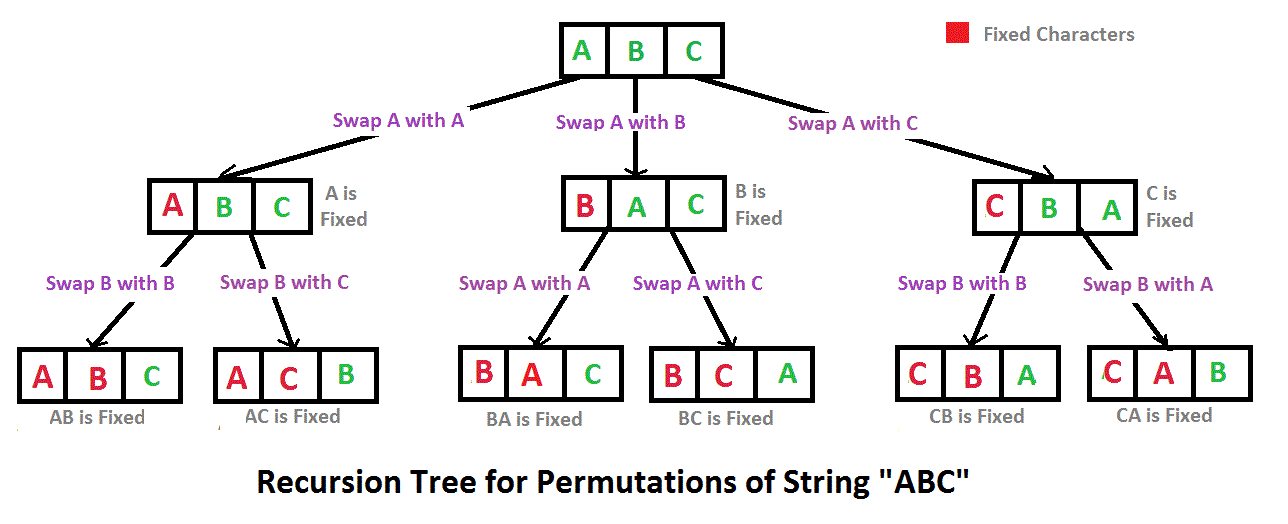
假設給你的字串有A個字元。

先放入第一個字元，我們可以產生A種遞迴的結果，然後針對於所有數量的結果，依序放入第二個字元，可以產生A-1種結果，然後第三個，可以產生A-2種結果，如果依序放入後，result字串的長度為A，則輸出。

數量即為$\mathop{\Pi_{c=0}^{c=A-1}}(A-c) = A!$

因此，我們就可以開始依照概念寫程式了。

## 模板(C++)

#include <bits/stdc++.h>
#define INF 1e6
using namespace std;

void printPermutation(int n,string str, string result, int complete){
	if(complete == n){
		cout << result << endl;
		return;
	}
	vector<char> vec(str.begin(),str.end());
	for(int i = 0; i < str.length(); i++){
		result[complete] = str[i];
		string remake = "";
		for(int j = 0; j < str.length(); j++){
			if(i == j) continue;
			remake += vec[j];
		}
		printPermutation(n,remake,result,complete+1);
	}
}

int main(){
	string str = "ABCDEFGH"; //遞迴字串
	string result = ""; 
        //我們先預設result有str.length()個字元，會比較好處理
	for(int i = 0; i < str.length(); result += 'x', i++);
	printPermutation(str.length(),str,result,0);
}

接下來，寫出模板之後，就可以開始寫C#的程式了

## 程式碼(C#)

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace problemA
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }
        private void printPermutation(int n, string str, string result, int complete)
        {
            if (complete == n)
            {
                listBox1.Items.Add(result);
                return;
            }
            char[] vec = str.ToCharArray();
            char[] rst = result.ToCharArray();
            for(int i = 0; i < vec.Length; i++)
            {
                rst[complete] = str[i];
                string remake = "";
                List<char> list = str.ToList<char>();
                list.RemoveAt(i);
                remake = String.Join("", list);
                result = String.Join("", rst);
                printPermutation(n, remake, result, complete + 1);
            }
        }

        private void button1_Click(object sender, EventArgs e)
        {
            listBox1.Items.Clear();
            String str = textBox1.Text;
            printPermutation(str.Length, str, "".PadLeft(str.Length, 'X'), 0);
            textBox2.Text = listBox1.Items.Count + "";
        }
    }
}