# 課程連結
[CS50 Artificial Intelligence](https://cs50.harvard.edu/x/2024/weeks/ai/#artificial-intelligence)
<iframe width="560" height="315" src="https://www.youtube.com/embed/6X58aP7yXC4?si=sf3FynyjcjYcOdPo" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe>
# 1. Image Generation
> 參考資料:
>- [基於 Diffusion Models 的生成圖像演算法](https://d246810g2000.medium.com/%E5%9F%BA%E6%96%BC-diffusion-models-%E7%9A%84%E7%94%9F%E6%88%90%E5%9C%96%E5%83%8F%E6%BC%94%E7%AE%97%E6%B3%95-984212710610)
>- [AIAIART #7](https://colab.research.google.com/drive/1NFxjNI-UIR7Ku0KERmv7Yb_586vHQW43?usp=sharing#scrollTo=g7btoXL7Im7M)
>- [原始論文:Denoising Diffusion Probabilistic Models](https://arxiv.org/abs/2006.11239)
## 常見圖片生成
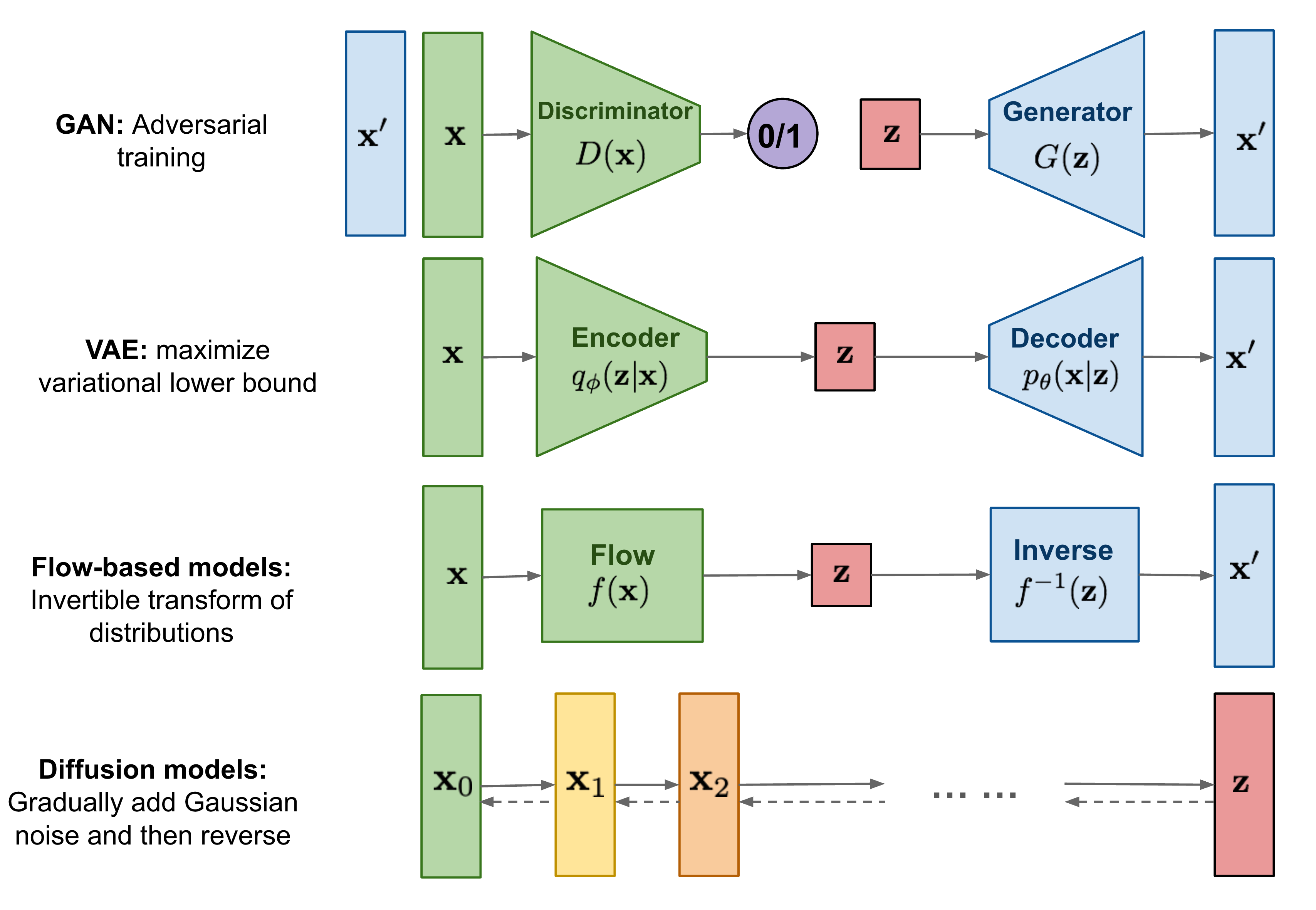
- Autoencoder [2006]
- Variational Autoencoder (VAE) [2014]
- Flow-based models
- GAN [2014]
- PixelRNN [2016]
- Diffusion [2020]
## Defusion Model
Defusion Model 是模仿Markov chain,利用常態分佈(高斯分佈)逐漸對一張圖片增加雜訊,直到看不到原始的圖片(下圖的q),再利用模型一步一步把圖片還原回來(下圖的p)

可以看下左這張圖逐漸從雜訊中生出一張圖。
<div style="display: flex; justify-content: space-around;">
<div style="text-align: center;">
<img src="https://miro.medium.com/v2/resize:fit:640/format:webp/1*4GmL_x9gzQu3uiH8JKdfaQ.gif" alt="Image 1" style="max-width:97%;">
<p>生成過程</p>
</div>
<div style="text-align: center;">
<img src="https://truth.bahamut.com.tw/s01/202304/4adfdcb747b978c794f5709339986662.JPG" alt="Image 2" style=";">
<p>我的train壞掉的版本</p>
</div>
</div>
### Diffusion process (擴散過程)
下面是的意思是,我們會逐步對一張圖片加上常態分配的雜訊,這個步驟總共會做T次,其中的一次叫做t。`Beta_t`是一個會隨著t越大而增加的值,而雜訊的常態分配的平均數(mean)是`Beta_t`*上一步驟t-1的圖片, 變異數(var)是`Beta_t`,可以算出雜訊eps, 接著新的圖片會是`main + √var*eps`。
我們模型要訓練的其實是給定一張被雜訊污染的`X_t`,要求模型幫我們預測出是什麼雜訊污染他,也就是預測`eps`
> 公式
$$
q(\mathbf{x}_{1:T} | \mathbf{x}_0) := \prod_{t=1}^T q(\mathbf{x}_t | \mathbf{x}_{t-1}), \quad
q(\mathbf{x}_t | \mathbf{x}_{t-1}) := \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t}\mathbf{x}_{t-1}, \beta_t \mathbf{I})
$$
```python=
n_steps = 100
beta = torch.linspace(0.0001, 0.04, n_steps)
def q_xt_xtminus1(xtm1, t):
# gat
mean = gather(1. - beta, t) ** 0.5 * xtm1 # √(1−βt)*xtm1
var = gather(beta, t) # βt I
eps = torch.randn_like(xtm1) # Noise shaped like xtm1
return mean + (var ** 0.5) * eps
def gather(consts: torch.Tensor, t: torch.Tensor):
"""
Gather consts for $t$ and reshape to feature map shape
用來提取一個tensor中第t個值,並錢reshape
"""
c = consts.gather(-1, t)
return c.reshape(-1, 1, 1, 1)
```
### Reverse process (逆擴散過程)
上面說到模型需要給定圖片`x_t`,預測雜訊`eps`,實際上是要讓模型學會產生`eps`的常態分配的平均值和標準差。
有了上面的`beta_t`,可以算出`alpha_t = 1 - beta_t`, `alpha_bar_t = 從 t=0 連乘到t=t`,接著按下面步驟算出:
1. 雜訊的係數 eps_coef = `(1-alpha_t )/ √(1-alpha_bar_t)`
2. 平均mean = `(1/(√alpha_t))*(x_t - eps_coef * noise)`
3. var: 就是`beta_t`
4. 新的雜訊eps: 用torch生成隨機數
5. 新的圖片 `main + √var*eps`
> 公式:
$$
p_\theta(\mathbf{x}_{0:T}) := p(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t), \quad
p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) := \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \Sigma_\theta(\mathbf{x}_t, t))
$$
```python=
# Set up some parameters
n_steps = 100
beta = torch.linspace(0.0001, 0.04, n_steps).cuda()
alpha = 1. - beta
alpha_bar = torch.cumprod(alpha, dim=0)
def p_xt(xt, noise, t):
"""
x_t:被污染的圖片
noise:模型看著x_t預測出來的雜訊
t:現在是第幾步驟
"""
alpha_t = gather(alpha, t)
alpha_bar_t = gather(alpha_bar, t)
eps_coef = (1 - alpha_t) / (1 - alpha_bar_t) ** .5
mean = 1 / (alpha_t ** 0.5) * (xt - eps_coef * noise) # Note minus sign
var = gather(beta, t)
eps = torch.randn(xt.shape, device=xt.device)
return mean + (var ** 0.5) * eps
```
### Algorithm 演算法

#### Loss Function
學習的時候會使用下面這個loss function來計算,其實就是算出污染`x_t`圖片的雜訊`eps_t`與模型預測的雜訊`pred_noise_t`平方差的平方 (mse)
$$
L_{\text{simple}}(\theta) := \mathbb{E}_{t, \mathbf{x}_0, \epsilon} \left[ \left\| \epsilon - \epsilon_\theta \left( \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t \right) \right\|^2 \right]
$$
#### Training
重複以下4個步驟直到loss降低
1.訓練時先從我們想訓練的圖片集(`q(x_theata`)中挑出一張 `x_theata`
2.設定總訓練步驟數大T(也就是上面設定的`n_step`),中**隨機**挑朱一個步驟做
3.先用常態分佈隨機出一個雜訊`eps`
4.用上面的loss function算出`eps`與模型預測的雜訊`pred_noise`的平方差的平方,然後做gradient descent
<div style="display: flex-ㄏㄠ; justify-content: space-around;">
<div style="text-align: left; width: 100%;;">
<b>Algorithm 1</b> Training
<pre>
1: repeat
2: <b>x</b><sub>0</sub> ~ <i>q</i>(<b>x</b><sub>0</sub>)
3: <i>t</i> ~ Uniform({1, ..., T})
4: <b>ε</b> ~ <i>𝒩</i>(0, <b>I</b>)
5: Take gradient descent step on
∇<sub>θ</sub> || <b>ε</b> - <b>ε</b><sub>θ</sub>(√<span style="text-decoration: overline;">α</span><sub>t</sub><b>x</b><sub>0</sub> + √1 - <span style="text-decoration: overline;">α</span><sub>t</sub><b>ε</b>, <i>t</i>) ||<sup>2</sup>
6: until converged
</pre>
</div>
</div>
#### Sampling
訓練好之後就可以來產圖了,產圖流程如下:
1. 先獲得一個雜訊,就做`x_T`
2. 執行大T(n_step)次去噪動作,以下為loop
1. 使用訓練好的model產生預測的雜訊`pred_eps`
1. 使用[Reverse process (逆擴散過程)](#Reverse-process-逆擴散過程)的公式,幫圖片降噪,並還要加上一個小雜訊
3. loop完之後圖片產出
<div style="display: flex-ㄏㄠ; justify-content: space-around;">
<div style="text-align: left; width: 100%;">
<b>Algorithm 2</b> Sampling
<pre>
1: <b>x</b><sub>T</sub> ~ <i>𝒩</i>(0, <b>I</b>)
2: for <i>t</i> = T, ..., 1 do
3: <b>z</b> ~ <i>𝒩</i>(0, <b>I</b>) if <i>t</i> > 1, else <b>z</b> = 0
4: <b>x</b><sub>t-1</sub> = <sup>1</sup>/<sub>√α<sub>t</sub></sub> (<b>x</b><sub>t</sub> - <sup>1 - α<sub>t</sub></sup>/<sub>√1 - <span style="text-decoration: overline;">α</span><sub>t</sub></sub> <b>ε</b><sub>θ</sub>(<b>x</b><sub>t</sub>, <i>t</i>)) + σ<sub>t</sub><b>z</b>
5: end for
6: return <b>x</b><sub>0</sub>
</pre>
</div>
</div>
### 模型 UNet
> 參考資料
>- [UNet 原始論文:U-Net: Convolutional Networks for Biomedical Image Segmentation](https://arxiv.org/abs/1505.04597)
>- [ConvTranspose2d原理,深度网络如何进行上采样?](https://blog.csdn.net/qq_27261889/article/details/86304061)
U Net 是用來預測雜訊 `pred_eps`的模型本體,他可以輸入兩個值:
1. 用來預測的被污染的圖片`x_t`
2. 現在是第幾個步驟t
步驟是
1. down: 2次的 3\*3 convolution 搭配一次2\*2 max pool,共執行4次
2. middle(bottom),兩次的convolution,在這裡要加數步驟t的embedding資訊,模型才會知道現在在第幾步驟
3. up:2次的 3\*3 convolution 搭配一次2\*2 up-conv(逆convolution),共執行4次

# 2. Deep Learning
> 參考資料
> - [李宏毅. 2016d. ML Lecture 6: Brief Introduction of Deep Learning. YouTube](https://www.youtube.com/watch?v=Dr-WRlEFefw.)
> - [李宏毅. 2016g. ML Lecture 11: Why Deep? YouTube.](https://www.youtube.com/watch?v=XsC9byQkUH8)
> - [李宏毅. 2016d. ML Lecture 6: Brief Introduction of Deep Learning. YouTube.](https://www.youtube.com/watch?v=Dr-WRlEFefw)
> - [李宏毅. 2017a. ML Lecture 5: Logistic Regression. YouTube.](https://www.youtube.com/watch?v=hSXFuypLukA)
> - [李宏毅. 2016a. ML Lecture 1: Regression - Case Study. YouTube.](https://tdr.lib.ntu.edu.tw/jspui/bitstream/123456789/8399/1/U0001-1204202115134100.pdf)
> - [Glorot, X., and Y. Bengio. 2010. Understanding the difficulty of training deep feedforward neural
networks. ](https://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf)
## 名稱的由來
1958年,Frank Rosenblatt 提出 Perceptron 演算法,用於線性分類。1962年,Marvin Minsky 批評其局限性,導致研究熱潮迅速平息。1980年代中期,Multilayer Perceptron(多層感知器)被提出,實際上是多層 Logistic Model 的連接,被稱為 Neural Network(神經網路)。1986年,Rumelhart 等提出 Back-propagation 演算法,可調整神經網路中各單元的權重。然而,隱藏層超過三層時效果不佳,1989年,多數學者認為一層隱藏層足夠。
1999年後,隨著GPU的發展,訓練多層隱藏層變得可能,Multilayer Perceptron 被重新命名為 Deep Learning(深度學習)。2006年,Hinton等人提出使用 Restricted Boltzmann machines (RBM) 來初始化深度學習的權重,吸引了許多研究者的關注。一些人認為使用RBM才算是深度學習,但隨著研究深入,發現不需要RBM也能訓練深度學習模型。因此,Deep Learning 與 Multilayer Perceptron(Neural Network)成為同一種演算法的不同名稱,「深度學習」與「神經網絡」常被交互使用。
## 深度學習5個組件
### 1. Activation Function
Activation function 是深度學習中最基本的單位,可以想像它是神經網路中的
一個節點(node),執行最簡單的非線性轉換。 常見的有Sigmoid 和 ReLU等:
> **Sigmoid 函數:**
$$
\sigma(x) = \frac{1}{1 + e^{-x}}
$$
> **ReLU 函數:**
$$
\text{ReLU}(x) = \max(0, x)
$$
Activation function 可以產生相當於邏輯運算子的效果,舉例來說,如果有四的點,分別為(0,0)、(1,0)、(0,1)、(1,1)。如果要將(0,0)與(1,1)分為一類,(1,0)與(0,1)分為另一類,會發現若單純使用一次方程會不能輕易區分。
但如果我們用以以下兩個Function做轉換
$$
\text{w} = \max(0, x - 0.5 y)
$$
$$
\text{z} = \max(0, -0.9x + y)
$$
轉換後的四個點分別為(0,0)、(0.5,0.1)、(1,0)、(0,1),就可以被一次方程分成兩邊。
<div style="display: flex; justify-content: space-around;">
<div style="text-align: center;">
<img src="https://hackmd.io/_uploads/SyXMZjjU0.png" alt="Image 1" style="max-width:95%;">
<p>轉換前</p>
</div>
<div style="text-align: center;">
<img src="https://hackmd.io/_uploads/SJY7Wss8R.png" alt="Image 2" style="max-width:100%;">
<p>轉換後</p>
</div>
</div>
### 2. 深度學習架構
深度學習架構可以靈活變化以滿足不同需求。這邊使用最基礎的 Fully Connected Feedforward Network 架構,由 Input Layer、Output Layer 和任意數量的 Hidden Layer 組成。
1. **Input Layer**:這一層並不是真正的一層,而是表示輸入向量。每個自變數都會輸入到下一層的所有節點中。
2. **Hidden Layer**:這層是由任意數量的 Activation Function 組成的,可以有多層。每層的節點數量和使用的 Activation Function 可以不同。例如,第一層可以使用5000個 Sigmoid 函數,而第二層可以使用3000個 ReLU 函數。從 Input Layer 得到的自變數在每個節點會產生一個值,這些值作為新的自變數輸入到下一層。每個 Hidden Layer 的輸出都會輸入到下一層的所有節點中,最終輸出到 Output Layer。
3. **Output Layer**:這一層作為分類器,將經過 Hidden Layer 非線性轉換的資料分類。例如,經過多層非線性轉換後,資料點會轉換成容易被分類的型態,找出資料的特徵(Feature),再利用 Output Layer 把資料分類成多個類別。常用的分類函數是 Softmax function,它將 hidden layer 中的資料壓縮到 0 到 1 之間,計算出每個類別的後驗機率,最大值對應的類別即為預測類別。
$$
\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{N} e^{x_j}}
$$
4. **Fully Connected Feedforward Network**:這是最常見的連接各層的方法。每個節點的輸出都會傳遞到下一層的所有節點,而每個節點也會使用上一層所有節點的輸出。這種結構被稱為 Fully Connected,資料從 Input Layer 傳遞到 Hidden Layer,再傳遞到 Output Layer,呈現順向結構。
這種架構允許任意改變以適應不同的需求,並提供了強大的靈活性和可擴展性,使其成為深度學習領域的基礎。
<div style="display: flex; justify-content: space-around;">
<div style="text-align: center;">
<img src="https://hackmd.io/_uploads/Hk94VsjU0.png" alt="Image 1" style="max-width:95%;">
<p>Fully Connected Feedforward Network</p>
</div>
</div>
### 3. Loss Function
在深度學習中,評估模型好壞需要使用 Loss Function。Loss Function 通過比較模型預測結果與真實資料來計算一個分數(Loss),分數越低表示預測結果越接近真實資料,模型性能越好。常用的 Loss Function 包括 Cross Entropy,特別是在分類任務中。
Cross Entropy 的優勢在於當模型預測與真實資料相差較大時,微分後的斜率較大,有助於訓練,而平方差公式在相同情況下則較平緩,不利於訓練。Loss Function 必須可微,以便使用 Gradient Descent 找出最符合真實情況的模型。根據不同情況,也可以選擇其他 Loss Function 或自定義 Loss Function。
> Cross Entropy
$$
L = -\sum_{i=1}^{N} y_i \log(\hat{y}_i)
$$
<div style="display: flex; justify-content: space-around;">
<div style="text-align: center;">
<img src="https://hackmd.io/_uploads/B1KWUiiIR.png" alt="Image 1" style="max-width:95%;">
<p>紅色為平方差,黑色為Cross Entropy</p>
</div>
</div>
### 4. Gradient Descent
想像模型中的每個權重 (weight) 代表空間中的一軸,把所有權重帶入 Loss Function 中形成高低起伏的空間,每個點表示一組權重計算出的 Loss。最佳模型擁有最低的 Loss,即整個空間中最底點的位置。計算全部權重組合的 Loss 會耗費大量資源,因此使用 Gradient Descent 來找出答案。
Gradient Descent 從 Loss 組成的波浪中選擇一個點,朝著該點斜率的反方向走一步,重複此步驟直到斜率為0的最底點。要得到此斜率需要把 Loss Function 對每一個權重做偏微分,得到的
值組成一個向量就叫做梯度(Gradient),可用符號∇表示
而為了要求得最低值,需要將原本的權重減去 Gradient,才會朝最低值前進。原先的點差距太遠而非像最低點前進,於是在減 Gradient 時會乘上一個數來限制Gradient 的步伐長度,這個數稱之為 Learning Rate,可用符號 η 表示。以上步驟可表示如下:
$$
w^{(T+1)} = w^{(T)} - \eta \nabla \text{Loss}(w^{(T)})
$$
除了基本的 Gradient Descent,還有許多變形方法,如每次只使用一筆資料的 Stochastic Gradient Descent、處理不均衡自變數的 Adagrad,結合動量概念的 Adam。
### 5. Backpropagation
> 參考影片:
<iframe width="540" height="400" src="https://www.youtube.com/embed/ibJpTrp5mcE?si=ITgK5Ima4WK61AVT" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe>
Backpropagation是在Deep Leaning Model中計算Gradient的方法,在計算之前我們要先了解微積分的Chain Rule。
> Chain Rule:
如果有兩個function如下
$$
\begin{aligned}
y &= g(x) \\
z &= h(y)
\end{aligned}
$$
則$x$對$z$的微分如下:
$$
\frac{\mathrm{d}z}{\mathrm{d}x} = \frac{\mathrm{d}z}{\mathrm{d}y} \cdot \frac{\mathrm{d}y}{\mathrm{d}x}
$$
又如果有一個值 $s$ 同時影響$x$和$y$, 而$x$和$y$又影響$z$:
$$
\begin{aligned}
x &= g(s) \\
y &= h(s) \\
z &= k(x,y)
\end{aligned}
$$
則$s$對$z$的微分如下
$$
\frac{\mathrm{d}z}{\mathrm{d}s} = \frac{\partial{z}}{\partial{x}} \cdot \frac{\mathrm{d}x}{\mathrm{d}s} + \frac{\partial{z}}{\partial{y}} \cdot \frac{\mathrm{d}y}{\mathrm{d}s}
$$
接著我們先定義深度學習模型會要使用的幾個function:
>activation function 用sigmoid function
$$
a = \sigma_{z}
$$
> 填入activation function中的$z$如下
$$
z = x_1w_1 +x_2w_2 +b
$$
> loss function 用 Cross Entropy
$$
L(\theta) = \sum_{n=1}^{N} C^n(\theta)
$$
> 也可以改寫如下
$$
\frac{\partial L(\theta)}{\partial w} = \sum_{n=1}^{N} \frac{\partial c^n(\theta)}{\partial w}
$$
從下圖可以看到完整的function邏輯,input layer傳入參數$x_1$, $x_2$,並與$w_1$, $w_2$, $b$組成 $z$, 將$z$帶入 activation function $\sigma{(z)}$產出$a$, $a$再作為下一層layer的參數。

為了要更新參數 $w$ ,我們需要用$w$對Loss function做偏微分,依照chain rule如下:
$$
\frac{\partial{C}}{\partial{w}} = \frac{\partial{z}}{\partial{w}} \cdot \frac{\partial{C}}{\partial{z}}
$$
而我們可以輕易知道$\frac{\partial{z}}{\partial{w_1}}$就是$x_1$,而這個$x_1$從上一層傳過來的,因此也叫做前向傳播。
> 前向傳播 (Forward Propagation)
$$
\begin{aligned}
\frac{\partial{z}}{\partial{w_1}} = x_1 \\
\frac{\partial{z}}{\partial{w_2}} = x_2
\end{aligned}
$$
而$\frac{\partial{C}}{\partial{w}}$後面的部分是:
$$
\frac{\partial{C}}{\partial{z}} = \frac{\partial{a}}{\partial{z}} \cdot \frac{\partial{C}}{\partial{a}}
$$
其中activation function $\sigma(z)$的微分已知:
$$
\frac{\partial{a}}{\partial{z}} = \sigma'(z)
$$
而$\frac{\partial{C}}{\partial{a}}$又可以繼續如下(因為$a$出來的值又會向下影響到下一層的參數function $z'$ 和 $z''$)
> Chain Rule
$$
\frac{\partial{C}}{\partial{a}} = \frac{\partial{z'}}{\partial{a}} \cdot \frac{\partial{C}}{\partial{z'}} + \frac{\partial{z''}}{\partial{a}} \cdot \frac{\partial{C}}{\partial{z''}}
$$
從上面的圖片我們可以知道
$$
\begin{aligned}
\frac{\partial{z'}}{\partial{a}} = w_1 \\
\frac{\partial{z''}}{\partial{a}} = w_2
\end{aligned}
$$
雖然$\frac{\partial{C}}{\partial{z'}}$和$\frac{\partial{C}}{\partial{z''}}$仍然未知,但我們先假設我們知道怎麼算,可以從上面的算是中得出
$$
\frac{\partial{C}}{\partial{z}} = \sigma'(x)\left[w_3 \cdot \frac{\partial{C}}{\partial{z'}} + w_4\cdot \frac{\partial{C}}{\partial{z''}}\right]
$$
最後假設$z'$和$z''$下一層就是進入Output layer並產出預測的結果$y_1$和$y_2$, 並有相對應的答案(Ground Truth) $\hat{y}_1$和$\hat{y}_2$,我們便可以算出$\frac{\partial{C}}{\partial{z'}}$和$\frac{\partial{C}}{\partial{z''}}$:
$$
\begin{aligned}
\frac{\partial{C}}{\partial{z'}} = \frac{\partial{y_1}}{\partial{z'}} \cdot \frac{\partial{C}}{\partial{y_1}} \\
\frac{\partial{C}}{\partial{z''}} = \frac{\partial{y_2}}{\partial{z''}} \cdot \frac{\partial{C}}{\partial{y_2}}
\end{aligned}
$$
而我們知道了$\frac{\partial{C}}{\partial{z'}}$和$\frac{\partial{C}}{\partial{z''}}$就可以算出$\frac{\partial{C}}{\partial{z}}$
$$
\frac{\partial{C}}{\partial{z}} = \sigma'(x)\left[w_3 \cdot \frac{\partial{y_1}}{\partial{z'}} \cdot \frac{\partial{C}}{\partial{y_1}} + w_4\cdot \frac{\partial{y_2}}{\partial{z''}} \cdot \frac{\partial{C}}{\partial{y_2}}\right]
$$
再搭配前向傳播的$x_1$可以組出來:
$$
\frac{\partial{C}}{\partial{w_1}} = x_1 \cdot \frac{\partial{C}}{\partial{z}} \cdot \sigma'(x)\left[w_3 \cdot \frac{\partial{y_1}}{\partial{z'}} \cdot \frac{\partial{C}}{\partial{y_1}} + w_4\cdot \frac{\partial{y_2}}{\partial{z''}} \cdot \frac{\partial{C}}{\partial{y_2}}\right]
$$
我們就可以用$\frac{\partial{C}}{\partial{w_1}}$去調整$w_1$了
---
# 3. Embedding 與 向量資料庫
> 參考資料:
> - [極速ChatGPT開發者兵器指南:跨界整合Prompt Flow、LangChain與Semantic Kernel框架](https://www.books.com.tw/products/0010987469)
> - [TinyMurky/embed_and_vector_database_practice](https://github.com/TinyMurky/embed_and_vector_database_practice)
## Embedding
Embedding 是大型語言模型開發中的一個重要關鍵技術,可以將文字轉成依照向量 (vector)的方式存在,方便輸入到深度學習的模型中。經由特殊Embedding模型embed後的文字,還可以讓類似詞意的文字在向量空間中在一起。Embedding也不一定要限制在詞,也可以針對整個句子的句義抽取出訊息變成 vector (像是Openai 可以提供將句子變成 1,536為度的向量)
### One-hard encoding
最簡單的Embedding是 one-hard encoding,就是一個跟字典一樣長的vector,在該詞的位置上標上1,其他都是0。
例如 `你好嗎?` 就可以變成 `你`, `好`, `嗎`的字典,並表示如下:
1. 你:`[1, 0, 0]`
2. 好:`[0, 1, 0]`
3. 嗎:`[0, 0, 1]`
這樣的好處是很好Embedding,壞處是vector會變得太長。
### Hugging Face
我們可以用Hugging face上的模型`all-MiniLM-L6-v2`來做embed,他會把一整個句子直接抽取成 384為度的向量,如下面所表示
```python=
from sentence_transformers import SentenceTransformer
class EmbeddingModel:
"""
this class is responsible for the embedding model
"""
def __init__(self, model_name="sentence-transformers/all-MiniLM-L6-v2"):
self.model: SentenceTransformer = SentenceTransformer(model_name)
def encode(self, text: list[str]):
"""
change the texts into embeddings
"""
return self.model.encode(text)
```
下面我們將三個句子做Embed
```python=
def main():
embedding_model = EmbeddingModel()
sentences = ["Hello, World!", "I am Kyaru!", "I am a virtual YouTuber!"]
embeddings = embedding_model.encode(sentences)
print("Dimension: ", len(embeddings[0])) # 384 個向量
print("embeddings: ", embeddings)
```
得到下面結果,三個長度為384的 float list
```
Dimension: 384
embeddings: [[-0.03817715 0.03291114 -0.0054594 ... -0.04089032 0.03187141
0.0181632 ]
[-0.03684668 -0.03121175 0.11125965 ... 0.00893893 -0.08519208
0.01065892]
[-0.03827702 -0.10684672 -0.0039953 ... 0.05886666 -0.01260292
-0.01910227]]
```
### 向量資料庫
向量資料庫可以把Embedding後的vector當作key,並在裡面存放資料。並且可以藉由向量的相似程度來搜尋出相似的資料,主要用在推薦系統,大型語言模型的RAG時使用等。
#### Qdrant
向量資料庫有很多種,下面介紹[Qdrant](https://qdrant.tech/), Qdrant是開源的Rust語言寫成的向量資料庫,並且可以在本地端用docker架設
##### docker compose
docker-compose.yml 如下設定
```yml=
services:
qdrant:
image: qdrant/qdrant:v1.6.1
restart: always
container_name: qdrant
ports:
- "6333:6333"
volumes:
- ./qdrant/storage:/qurant/storage
- ./qdrant/config.yaml:/qurant/config/production.yaml
```
上面比較重要的是 volumn的設定。
- `/qurant/storage`:是設定向量資料庫真實的檔案是要存在你的電腦裡面的哪裡,我就是存在專案資料夾下面的 `./qdrant/storage` 資料夾
- `/qurant/config/production.yaml`:是設定Qdrand config檔在你的電腦上的真實位置,像是我的就是在專案資料夾下面的 `./qdrant/config.yaml`。
- config.yaml下載:[點我](https://github.com/qdrant/qdrant/blob/master/config/config.yaml)
另外在config.yaml找到 下面這個部份可以設定密碼
```yaml
service:
api_key: your_secret_api_key_here
```
接著在comand line中輸入下面指令就可以啟用了
```
docker-compose up -d
```
##### Qdrand Python SDK
Qdrand有提供Python 的SDK,可使用pip下載
```
poetry add qdrant-client openai
```
以下的是完整的程式碼,解說在後面
```python=
from app.embedding.model import EmbeddingModel
from qdrant_client import QdrantClient
from qdrant_client.http import models
from qdrant_client.http.models import PointStruct
class QdrantSingleton:
_instance = None
_initialized = False
def __new__(cls, *args, **kwargs):
if not cls._instance:
cls._instance = super(QdrantSingleton, cls).__new__(cls)
return cls._instance
def __init__(self):
if not QdrantSingleton._initialized:
self.qdrant_client = QdrantClient(
url="http://localhost",
port=6333,
# api_key="api_key",
)
self.embedding_model = EmbeddingModel()
QdrantSingleton._initialized = True
def recreate_collection(self, collection_name: str):
"""
這個方法會重新建立collection,並設定collection的參數
https://ithelp.ithome.com.tw/articles/10335513
"""
# https://python-client.qdrant.tech/qdrant_client.http.models.models#qdrant_client.http.models.models.VectorParams
# 一個用cosine算距離的向量,長度是384
vectors_config = models.VectorParams(
distance=models.Distance.COSINE,
size=384,
)
# m代表每個節點近鄰數量。m值越大,查詢速度越快,但內存和構建時間也會增加。
# ef_construct這是用於構建圖時的效率參數。較大的ef_construct值會導致更好的查詢品質,但會增加構建時間。代表在構建索引時搜索的節點數量
hnsw_config = models.HnswConfigDiff(on_disk=True, m=16, ef_construct=100)
# memmap_threshold是這表示當數據大小超過20000時,將使用內存映射來管理數據,這可以有效地處理大量數據並減少內存使用。
optimizers_config = models.OptimizersConfigDiff(memmap_threshold=20000)
self.qdrant_client.recreate_collection(
collection_name=collection_name,
vectors_config=vectors_config,
hnsw_config=hnsw_config,
optimizers_config=optimizers_config,
)
return self.qdrant_client
def create_collection(self, collection_name: str):
"""
create collection
"""
vectors_config = models.VectorParams(
distance=models.Distance.COSINE,
size=384,
)
hnsw_config = models.HnswConfigDiff(on_disk=True, m=16, ef_construct=100)
optimizers_config = models.OptimizersConfigDiff(memmap_threshold=20000)
if not self.qdrant_client.collection_exists(collection_name):
self.qdrant_client.create_collection(
collection_name=collection_name,
vectors_config=vectors_config,
hnsw_config=hnsw_config,
optimizers_config=optimizers_config,
)
return self.qdrant_client
def get_embedding(self, text: str) -> list[float]:
"""
get embedding
"""
embedding_list = self.embedding_model.encode([text])
embedding = embedding_list[0]
embedding_to_float_list = embedding.tolist()
return embedding_to_float_list
def upsert_vectors(
self, vectors: list[list[float]], collection_name: str, data: list
):
"""
upsert vectors
payload is metadata, can be any data in dict
"""
for i, vector in enumerate(vectors):
self.qdrant_client.upsert(
collection_name=collection_name,
points=[
PointStruct(
id=i,
vector=vector,
payload=data[i],
)
],
)
print("upsert_vectors done")
def search_for_qdrant(self, text: str, collection_name: str, limit_k: int):
"""
search for qdrant
"""
embedding_vector = self.get_embedding(text)
search_result = self.qdrant_client.search(
collection_name=collection_name,
query_vector=embedding_vector,
limit=limit_k,
append_payload=True,
)
return search_result
```
這邊看起來叫複雜,但其實這個是python的Singleton的寫法,在呼叫這個class的時候都只會回傳同一個init。最重要的是`QdrantClient`,這裡要放和Qdrant的連線資訊,另外EmbeddingModel則是上面的Class引入。
```python=
class QdrantSingleton:
_instance = None
_initialized = False
def __new__(cls, *args, **kwargs):
if not cls._instance:
cls._instance = super(QdrantSingleton, cls).__new__(cls)
return cls._instance
def __init__(self):
if not QdrantSingleton._initialized:
self.qdrant_client = QdrantClient(
url="http://localhost",
port=6333,
# api_key="api_key",
)
self.embedding_model = EmbeddingModel()
QdrantSingleton._initialized = True
```
接著我們要在向量資料庫中建立一個collection,collection就像是一般資料庫的table,用來存放我們的資料,由於是練習,我選擇使用`recreate_collection`,這樣如果呼叫撞名的collection就可以先刪除再重新創一個,如果不想一直刪除也可以選擇上面的`create_collection`
在這裡我們可以用`VectorParams`設定向量之間的距離怎麼算,我選擇COSINE,也可以用`models.Distance.EUCLID`選擇兩點直線距離。
並且`VectorParams`還可以設定當作key的vector的長度有多長,因為我使用Hugging face的`all-MiniLM-L6-v2`固定會產生 384 維度的vector,所以寫384
```python=
def recreate_collection(self, collection_name: str):
"""
這個方法會重新建立collection,並設定collection的參數
https://ithelp.ithome.com.tw/articles/10335513
"""
# https://python-client.qdrant.tech/qdrant_client.http.models.models#qdrant_client.http.models.models.VectorParams
# 一個用cosine算距離的向量,長度是384
vectors_config = models.VectorParams(
distance=models.Distance.COSINE,
size=384,
)
# m代表每個節點近鄰數量。m值越大,查詢速度越快,但內存和構建時間也會增加。
# ef_construct這是用於構建圖時的效率參數。較大的ef_construct值會導致更好的查詢品質,但會增加構建時間。代表在構建索引時搜索的節點數量
hnsw_config = models.HnswConfigDiff(on_disk=True, m=16, ef_construct=100)
# memmap_threshold是這表示當數據大小超過20000時,將使用內存映射來管理數據,這可以有效地處理大量數據並減少內存使用。
optimizers_config = models.OptimizersConfigDiff(memmap_threshold=20000)
self.qdrant_client.recreate_collection(
collection_name=collection_name,
vectors_config=vectors_config,
hnsw_config=hnsw_config,
optimizers_config=optimizers_config,
)
return self.qdrant_client
```
呼叫之後進入[localhost:6333/dashboard](http://localhost:6333/dashboard)應該可以看到下面的面

以下則是利用Hugging face的`all-MiniLM-L6-v2`將文字產出vector,我設計成一次用一個句子embedding,但要注意回傳的embedding會是 tensor, shape是(1, 384),所以要拿出第0個之後呼叫to_list,轉成float array後才能放入Qdrant
```python=
def get_embedding(self, text: str) -> list[float]:
"""
get embedding
"""
embedding_list = self.embedding_model.encode([text])
embedding = embedding_list[0]
embedding_to_float_list = embedding.tolist()
return embedding_to_float_list
```
接著可以用upsert(其實insert也可以)的方法,把vector當作key, data當作value(在Qdrant裡面叫做payload),data可以是任何型態的資料組成的array,像是python 的dictionary, 會存成json的形式
```python=
def upsert_vectors(
self, vectors: list[list[float]], collection_name: str, data: list
):
"""
upsert vectors
payload is metadata, can be any data in dict
"""
for i, vector in enumerate(vectors):
self.qdrant_client.upsert(
collection_name=collection_name,
points=[
PointStruct(
id=i,
vector=vector,
payload=data[i],
)
],
)
print("upsert_vectors done")
```
最後是查詢,只要提供一段文字,會先進行embed之後,用這個vector去資料庫查詢,並查出最接近的`limit_k`的資料,然後把裡面的payload拿出來。
```python=
def search_for_qdrant(self, text: str, collection_name: str, limit_k: int):
"""
search for qdrant
"""
embedding_vector = self.get_embedding(text)
search_result = self.qdrant_client.search(
collection_name=collection_name,
query_vector=embedding_vector,
limit=limit_k,
append_payload=True,
)
return search_result
```
##### Qdrant實戰演練
以下是我有`American Idiots`前四句的歌詞,我們把他一個一個embed好,再用embed的vector當作key, 把歌詞的資料當作payload存在向量資料庫
```python=
def main():
# qdrant
american_idiots = [
{"id": "1", "lyric": "Don't wanna be an American idiot"},
{"id": "2", "lyric": "Don't want a nation under the new media"},
{"id": "3", "lyric": "And can you hear the sound of hysteria?"},
{"id": "4", "lyric": "The subliminal * America"},
]
qdrant = QdrantSingleton()
collection_name = "Lyrics"
qdrant.recreate_collection(collection_name)
embedding_array = [qdrant.get_embedding(text["lyric"]) for text in american_idiots]
qdrant.upsert_vectors(embedding_array, collection_name, american_idiots)
```
在 [localhost:6333/dashboard](http://localhost:6333/dashboard)中可以看到已經存進去了。

接著我們用一句話進去搜查,並且設定我們只想要找到最相近的一個值
```python=
query_text = "stupid american"
search_result = qdrant.search_for_qdrant(query_text, collection_name, limit_k=1)
print(f"尋找: {query_text}", search_result)
```
output可以看到最接近的歌詞是`"Don't wanna be an American idiot"`
```
尋找: stupid american [ScoredPoint(id=0, version=0, score=0.5378643, payload={'id': '1', 'lyric': "Don't wanna be an American idiot"}, vector=None, shard_key=None)]
```
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet