# 排序與二分搜
## 二分搜概念
二分搜能運用到的場合相當多,只要是**單調區間**便可使用二分查找,主要的題目類型有:
* 尋找特定值
* 查找第一個大於等於某數的元素
* 查找最後一個小於等於某數的元素
* ...
二分搜說難也難、說簡單也簡單,主要是實作過程中有**許多細節**需要注意:
* left ,right要初始為(0,n-1)還是(0,n)?
* while判斷式中要填left<=right還是left<right?
* 更新left和right時mid要+1還是-1?
就這些細節可知二分搜有許多類型和細節,為求解題方便以下將提出一套思路使你在面對各類型的題目時,都能輕易找出對應的寫法。
---
# 實作
## 大於等於
### 問題定義
給定一**單調上升之數列**,求第一個**大於等於某特定值**的元素索引值並定義其為「下界」,當下界不存在則回傳數組長度。
### 思路
給定數組[1,2,4,5,5,6,7],令特定值為5則應該回傳下界為3
| 0 | 1 | 2 | ->3 | 4 | 5 | 6 |
| --- | --- | --- |:---:| --- | --- | --- |
| 1 | 2 | 4 | ->5 | 5 | 6 | 7 |
可以看到我們能將數列分為**右側都大於等於特定值**和**左側都小於特定值**,而我們回傳之索引值正好是**大於等於特定值的數列之下界**。
首先,我們以**閉區間**之寫法來表達思路:
* 區間範圍為[left,right],left指向索引值0,right指向索引值6
* mid為[left,right]的中間位置
* **當left>right時,區間為空**
依據上述思路提出,演算法步驟:
1. 若arr[mid]>=特定值,則[mid,right]區間內所有元素均大於等於特定值,因此right左移,故**right=mid-1**。
2. 否則,則是[left,mid]區間內所有元素均小於特定值,因此left右移,故**left=mid+1**。
3. 重複上述動作直到區間被刪減為空,**此時left將會停在下界,故回傳left**。
### 程式碼
可執行下列程式碼以利思考。
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int a[100005];
int main(){
int n,x;
cin>>n;
for(int i=0;i<n;++i)cin>>a[i];
cin>>x;
sort(a,a+n);
int left=0,right=n-1;//[0~N-1]的閉區間
while(left<=right){//[left~right]大小為零結束
int mid=(right+left)/2;
//cout<<left<<' '<<mid<<' '<<right<<'\n';
if(a[mid]>=x) right=mid-1;
else left=mid+1;
}
cout<<left<<'\n';//回傳索引值
return 0;
}
```
## 小於等於
### 問題定義
給定一**單調上升之數列**,求最後一個**小於等於某特定值**的元素索引值並定義其為「上界」。
### 思路
一樣給定數組 [1,2,4,5,5,6,7],令特定值為5則應該回傳上界為4
| 0 | 1 | 2 | 3 | ->4 | 5 | 6 |
| --- | --- | --- | --- | --- | --- | --- |
| 1 | 2 | 4 | 5 | ->5 | 6 | 7 |
首先我們一樣能將數列分為右側都大於特定值和左側都小於等於特定值,透過觀察我們可以發現,**小於等於特定值的數列上界和大於特定值下界是相鄰的**所以 **上界 = 下界 - 1**。因此,所有找上界的问题,都可以**轉換為「互補的」找下界的問题**。
* 區間範圍為[left,right],left指向索引值0,right指向索引值6
* mid為[left,right]的中間位置
* **當left>right時,區間為空**
* 這次要查找的元素為大於特定值,故**right判斷式要改為a[mid]>x**
依據之前的思路提出相同的演算法步驟:
1. 若arr[mid]>=特定值,則[mid,right]區間內所有元素均大於等於特定值,因此right左移,故**right=mid-1**。
2. 否則,則是[left,mid]區間內所有元素均小於特定值,因此left右移,故**left=mid+1**。
3. 重複上述動作直到區間被刪減為空,**此時left將會停在下界而right會停在left-1的位置即為「上界」,故回傳right**。
## 程式碼
可執行下列程式碼以利思考。
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int a[100005];
int main(){
int n,x;
cin>>n;
for(int i=0;i<n;++i)cin>>a[i];
cin>>x;
sort(a,a+n);
int left=0,right=n-1;//[0~N-1]的閉區間
while(left<=right){//[left~right]大小為零結束
int mid=(right+left)/2;
//cout<<left<<' '<<mid<<' '<<right<<'\n';
if(a[mid]>x) right=mid-1;
else left=mid+1;
}
cout<<right<<'\n';//回傳索引值
return 0;
}
```
---
# 總結
二分搜無論是找下界、還是找上界,都可以套用「找下界」的思路來實作:
* 首先是循環條件 若是閉區間的話以left <= right,表示區間不為空,開區間則是以left < right,表示區間不為空。
* 再來if的判定條件和問題的比較規則是相同的,比如要找**满足 x >= target 的第一个元素**,就令 **if a[mid] >= target**;要找**滿足 x > target 的第一个元素**,**就令 if a[m] > target**。
* 接著if為真時,以**閉區間**為例需更新 **right:right = mid - 1**;否則 **left = mid + 1**;而**開區間**則是更新 **right:right = mid** ;否則 **left = mid + 1**。
* 最後當循環结束時,**閉區間**的**left會指向下界**,**right則指向「互補條件」的上界**;而**開區間**的**left和right則都指向下界**
---
# 補充
## 開區間二分搜寫法
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int a[100005];
int main(){
int n,x;
cin>>n;
for(int i=0;i<n;++i)cin>>a[i];
cin>>x;
int left=0,right=n;//[0~N-1]的開區間
while(left<right){//[left~right)大小為零結束
int mid=(right+left)/2;
//cout<<left<<' '<<mid<<' '<<right<<'\n';
if(a[mid]>=x) right=mid;
else left=mid+1;
}
cout<<left<<'\n';//回傳索引值
return 0;
}
```
## c++二分搜函式
1. **lower_bound( begin,end,num,greater() )**:從陣列的begin位置到end-1位置二分查詢第一個小於或等於num的數字,找到返回該數字的地址,不存在則返回end。
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int a[100005];
int main(){
int n,x;
cin>>n;
for(int i=0;i<n;++i)cin>>a[i];
cin>>x;
cout<<lower_bound(a,a+n,x)-a<<'\n';
//通過返回的地址減去起始地址begin,得到索引值
return 0;
}
```
2. **upper_bound( begin,end,num,greater() )**:從陣列的begin位置到end-1位置二分查詢第一個小於num的數字,找到返回該數字的地址,不存在則返回end。
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int a[100005];
int main(){
int n,x;
cin>>n;
for(int i=0;i<n;++i)cin>>a[i];
cin>>x;
cout<<upper_bound(a,a+n,x)-a<<'\n';
//通過返回的地址減去起始地址begin,得到索引值
return 0;
}
```
3. **binary_search( begin,end,num,greater() )**:從陣列的begin位置到end-1位置二分查詢num是否存在陣列中,找到返回True,不存在則返回False。
```cpp
#include<bits/stdc++.h>
using namespace std;
int a[100005];
int main(){
int n,x;
cin>>n;
for(int i=0;i<n;++i)cin>>a[i];
cin>>x;
if(binary_search(a,a+n, x))
cout << "found" <<'\n';
else
cout << "not found" <<'\n';
return 0;
}
```
## 習題
### [APCS_2022/1 4.牆上海報](https://zerojudge.tw/ShowProblem?problemid=h083)
---
### Safe Sorter
#### 題目敘述 :
我們的保險箱現在要放到一個分類器之中,此分類器有許多節點(如下圖),放入的規則如下。
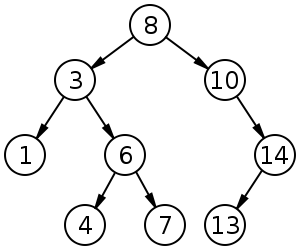
- 如果該節點還沒有任何保險箱,此保險箱就會佔據該節點
- 否則若這個要放入的保險箱裡面的金塊比在該節點的保險箱還要多,他會被往右邊送
- 否則就往左邊送
- 必須送到他占用一個節點為止
以上圖為例
- 第一個放進來的保險箱有 8 個金塊
- 第二個有 10 個,因此他被放在右邊
- 第三個有 14 個,因此第一步會先往右送,發現右邊的節點也有保險箱了,因而再次被往右送
- 第四個有 3 個,於是被放在左邊
- 其他依此類推
由於分類器內部構造太大,不方便進入,所以開發者有再分類器中內建一套電梯探訪順序,以及記錄規則供使用者參考,避免保險箱被重複計算或是漏算。如下
- 當此節點的左邊有保險箱,電梯優先向左
- 當此節點的左邊的保險箱都被記錄過了,或是左邊根本沒有保險箱,紀錄當前所在的節點裡面保險箱的金條數量
- 然後電梯向右
同樣以上圖為例
- 節點 8 的左邊有其他保險箱 >> 電梯向左
- 進到節點 3 >> 同上 >> 電梯向左
- 進到節點 1 >> 左右邊都沒有保險箱 >> 記下 1 >> 電梯回到節點 3
- 左邊都記錄過了 >> 記下 3 >> 右邊有保險箱 >> 電梯向右
- 進到節點 6 >> 左邊有其他保險箱 >> 電梯向左
- 進到節點 4 >> 左右邊都沒有保險箱 >> 記下 4 >> 電梯回到節點 6
- 左邊都記錄過了 >> 記下 6 >> 右邊有保險箱 >> 電梯向右
- 進到節點 7 >> 左右邊都沒有保險箱 >> 記下 7 >> 電梯回到節點 6
- 電梯回到節點 3 >> 電梯回到節點 8 >> 左邊保險箱紀錄完畢 >> 記下 8 >> 右邊有保險箱 >> 電梯向右
- 進到節點 10 >> 左邊沒有保險箱 >> 記下 10 >> 右邊有保險箱 >> 電梯向右
- 進到節點 14 >> 左邊有保險箱 >> 電梯向左
- 進到節點 13 >> 左右邊都沒有保險箱 >> 記下 13 >> 電梯回到節點 14
- 左邊保險箱紀錄完畢 >> 記下 14
- 電梯回到節點 10 >> 電梯回到節點 8
- 紀錄完畢
最後結果如下
```
1 3 4 6 7 8 10 13 14
```
#### 輸入說明 :
- 第一行輸入 $1$ 個數字 $t$ ,代表有 $t$ 比測試資料
- 每筆測資第一行輸入 $1$ 個數字 $n$ ,表示一開始的保險箱有幾個
- 第二行輸入 $n$ 個數字 $a_1,a_2...a_n$ , $a_i$ 代表第 $i$ 個放入分類器的保險箱有幾塊金條
$t \leq 10$
$n$ $,$ $a_i$ $\leq 10^5$
#### 輸出說明 :
僅全部的保險箱放完以後進行一次紀錄
#### 範例輸入1 :
```
2
3
3 2 1
9
8 10 14 3 1 6 7 4 13
```
#### 範例輸出1 :
```
1 2 3
1 3 4 6 7 8 10 13 14
```
#### 子題組與配分
- 第一子題組 : 放入的順序為由大到小,占 10%
- 第二子題組 : 無其他限制,占 90%
---
### 睿璿的煩惱
#### 題目敘述:
睿璿學長很喜歡一個射擊遊戲,其中有許多難度不同的極限挑戰,皆由數以萬計的關卡組成。玩家要在不死亡的前提下通過所有關卡,且同一組挑戰內通過關卡**並不會**回復至初始血量,並且玩家可以攜帶**限定數量以下(含)的大型生命補給與彈藥儲轉箱**,分別可以將生命值與備彈補充至**全滿**。睿璿學長已經練習到可以百發百中,且**通過一關僅需要一分鐘**。然而他發現他的等級並不一定足夠通過所有關卡。請你幫幫他。
#### 輸入說明:
第一行有$3$個數字 $n,hl,al$,分別代表關卡數,大型生命補給與彈藥儲轉箱的使用上限
第二行有$n$個數字 $amo_1,amo_2...amo_n$,代表各個關卡需要消耗的子彈數目
第三行有$n$個數字 $hpc_1,hpc_2...hpc_n$,代表各個關卡需要消耗的生命值
第四行有$4$個數字 $a,b,c,d$,分別代表等級與生命值上限/攜帶彈藥上限的關係,如右式 $ax+b, cx+d$。
最後一行有兩個數字 $LvT,lv$,分別代表每升一級所需的時間(單位:分鐘)和他現在的等級。
#### 輸出說明:
請輸出一行 $t$ $lv$,分別是花費的時間、過關後的等級。
#### 測資規模:
$n \leq 10^5$
$hl,al \leq 25$
$1 \leq a,b,c,d \leq 10$
$amo_{i}$ $,$ $hpc_{i}\leq 10^5$
#### 範例輸入:
```
1 0 0
5
10
1 1 1 1
2 100
```
#### 範例輸出:
```
1 100
```
---
###### tags: `APCS與競賽入門`
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet