# TSS

## Overview

Before diving into the topic of TSS, readers should be familiar with the concepts of elliptic curves, Schnorr and ECDSA signatures, Shamir's secret sharing, and ElGamal encryption. These ideas will help you grasp the underlying principles and mechanics of TSS, which is built on these foundational technologies.

- Elliptic Curves
- Schnorr & ECDSA
- Shamir's secret sharing
- ElGamal encryption

Typically, $(t,n)$-threshold signature schemes allow a group of $n$ participants to share a secret $s$, with the requirement that any $t$ of the $n$ participants cooperate in order to recover $s$, but any subset of fewer than $t$ participants cannot recover any information about the secret $s$.

TSS is a signature scheme that reduces network overhead while also protecting against forgery attacks. The protocol improves on previous Schnorr threshold signature protocols by allowing signing operations to take place in a single round while still requiring a minimum number of signers to participate. In the presence of a misbehaving participant, TSS can also safely abort. Following TSS, there is an improved version called identifiable-corrupted-entity, which can detect and exclude cheating participants during the Key Generation phase.

TSS protocol is based on the its new signature scheme. For the initial setup of the protocol, we have the following conditions:

- $P = \{P_1,P_2,...,P_n\}$ is the set of participants, where $|P| = n$. The threshold value $t$ and the $n$ participants are determined before the start of the protocol.
- $G_{sg}$ is a subgroup of an elliptic curve $E$ in which the Diffie–Hellman problem is considered hard, and $G$ is a generator point of that subgroup.
- Each participant $Pi , \; 1 ≤ i ≤ n$, is assigned a private key $sk_i$ randomly selected from $Z_q$ and a public key $pk_i = sk_iG$.
- The encryption scheme $En_{sym} = (Enc_{sym}, Dec_{sym})$ is associated with the key space $G_{sg}$, the message space $Z_q$, and the ciphertext space $C$.
- All participants use a public platform to facilitate communication and data aggregation. For example, during the key generation, the platform serves as a medium for each participant to share the knowledge of their generated polynomials and secret keys, as well as a means for the participants to reach a consensus on the long-lived public key and secret key. A public blockchain is one example of such a platform because it enables the decentralized and transparent sharing of information among all participants while providing a secure and tamper-proof way to store the data.

The protocol is composed of two sub-protocols: Key Generation and Signing.

1. **Key Generation Protocol:**
All parties involved contribute to the creation and distribution of a shared secret key that will be used to sign messages. Unlike threshold schemes that rely on a trusted dealer, such as Shamir secret sharing, the protocol employs Distributed Key Generation (DKG) to ensure that every participant contributes equally to the generation of the shared secret. Each participant selects a secret, generates a polynomial, and publishes a proof of knowledge of the secret with zero knowledge. The public key of the group $Y$ is calculated using all of the participants' commitments. There are two rounds of key generation.
1. In the first round, each participant $P_i$ generates their polynomial and one-time use a secret key $sk_i$(just for the encryption and decryption during the key generation) by randomly selecting $t$ coefficients and a secret key from $Z_q$, then broadcasts their knowledge of their polynomial and secret key to the public.
2. The second round involves all participants sending their partial secrets or shares to others in order to generate the long-lived secret key after receiving all partial secrets or shares from others that will be used in the signing protocol.
2. **Signing Protocol:**
The signing protocol consists of two distinct but dependent processes: preprocessing and signing.
1. In the preprocessing, each participant $P_i$ generates a list of single-use private nonce pairs $(d_{i},e_{i})$ and corresponding public commitment $(D_{i}, E_{i})$, which are then published independently from the signing process. The preprocess commitments can be made independently to ensure that there are enough commitments on the list to allow the signing to take place.
2. There is only one round of signing. When a message $m$ needs to be signed, an external mechanism can choose a set $S$ of ids of at least $t$ signers or $S \subseteq \{1,2,3,...,n\}$ where $|S| \geq t$, and the next available commitment $(D_{l}, E_{l})$ is applied to each signer $P_l$ where $l \in S$. The public platform then calculate a binding value $ρ_l$, a group commitment $R$, and a challenge $c$ using hash functions $H$. Each signer $P_l$ only submit their signature $z_l$ according to the challenge $c$ . After the platform receiving all $z_{l \in S}$, the platform checks the consistency of the responses, and if they pass, the group's response is calculated, resulting in the final signature $(R,z)$. This signature is verifiable using a standard Schnorr verification operation with the group's public key $Y$.

## Key Generation Protocol

Let $H_1$, $H_2$, and $H_3$ be three collision-resistant hash functions whose output is in $Z_q$, the $Enc_{sym}, \; Dec_{sym}$ be the ElGamal encryption and decryption scheme, and $PB$ is a public blockchain capable of aggregating and validating data from participants.

### **Round 1**

1. The $PB$ or any external mechanism is used to determine the set of participants $P = \{P_1,P_2,P_3,...,P_n\}$, the threshold $t \leq n$, and the key generation context string $Φ$. The context string $Φ$ is used to prevent the replay attack, which can be any one-time-use string, such as the current block hash on $PB$.
2. For $i \in \{1,2,3,...,n\}$, each participant $P_i$ samples $t$ random positive integer values $a_{i0},a_{i1},a_{i2},...,a_{i(t-1)} \in Z_q$ and uses them as coefficients to define a degree $t-1$ polynomial $f_i(x) = \sum_{j=0}^{t-1} a_{ij}x^{j} = a_{i0} + a_{i1}x + a_{i2}x^2 + ... + a_{i(t-1)}x^{t-1}$.

> For all $i \in \{1,2,3,...,n\}$, each $P_i$’s secret polynomial $f_i(x)$ will be used to compute together on behalf of the group's secret polynomial $f(x)$ in the signing process, which means that the computation of the group's secret polynomial $f(x)$ can be done without anyone knowing what the actual group's secret polynomial $f(x)$ is.

The group's secret polynomial $f(x)$ can be written as follow:

$f(x) = \sum_{i=1}^{n} f_i(x) \\~\\
f(x) = f_1(x) + f_2(x) + ... + f_n(x) \\~\\
f(x) = (a_{10}+a_{11}x+...+a_{1(t-1)}x^{t-1})+(a_{20}+a_{21}x+...+a_{2(t-1)}x^{t-1})+...+(a_{n0}+a_{n1}x+...+a_{n(t-1)}x^{t-1}) \\~\\
f(x) = (a_{10}+a_{20}+...+a_{n0}) + (a_{11}+a_{21}+...+a_{n1})x + ...+ (a_{1(t-1)}+a_{1(t-1)}+...+a_{n(t-1)})x^{t-1} \\~\\
f(x) = (\sum_{i=1}^{n} a_{i0}) + (\sum_{i=1}^{n} a_{i1})x + ...+ (\sum_{i=1}^{n} a_{i(t-1)})x^{t-1} \\~\\
f(x) = a_0 + a_1x + ...+ a_{t-1}x^{t-1}$

As a result, the above equation implies that
$a_k = \sum_{i=1}^{n} a_{ik}$ for all $k \in \{0,1,2,...,t-1\}$.

However, the value of $\{a_0,a_1,a_2,...,a_{t-1}\}$ will never be revealed because the group's secret polynomial $f(x)$ must be kept secret from all.
>
3. Each participant $P_i$ computes the proof of knowledge of their secret value $a_{i0}$ by calculating as follow:
1. randomly select a one-time-use nonce $r_i \in Z_q$
2. calculate a commitment $R_i = r_iG$ where $G$ is the generator point
3. calculate the challenge $c_i = H_1(i, \; Φ, \; a_{i0}G , \; R_i)$ with $Φ$ being a context string to prevent replay attacks
4. calculate $µ_i = r_i + c_ia_{i0}$
5. define $σ_i = (R_i, µ_i)$

This proof of knowledge generation can be seen as a standard Schnorr signature by using $a_{i0}$ as a secret key with the additional context $i, Φ$.

4. Each participant $P_i$ samples $sk_i \in Z_q$ randomly and computes $Pk_i = sk_iG$.
5. Each participant $P_i$ computes a proof of knowledge of the secret key $sk_i$ by calculating as follow:
1. randomly select a one-time-use nonce $ŕ_i \in Z_q$
2. calculate a commitment $Ŕ_i = ŕ_iG$ where $G$ is the generator point
3. calculate the challenge $ć_i = H_2(i, \; Φ, \; Pk_i , \; Ŕ_i)$ with $Φ$ being a context string to prevent replay attacks
4. calculate $ν_i = ŕ_i + ć_isk_{i}$
5. define $τ_i = (Ŕ_i, ν_i)$

This is like the step 3.

6. Each participant $P_i$ compute a public commitment $C_i = \{ϕ_{i0},ϕ_{i1},ϕ_{i2},..., ϕ_{i(t-1)}\}$, where $ϕ_{ij} = a_{ij}G$ for $0 ≤ j ≤ t − 1$.
7. Each participant $P_i$ broadcasts $(C_i, \; σ_i, \; Pk_i, \; τ_i)$ to $PB$.


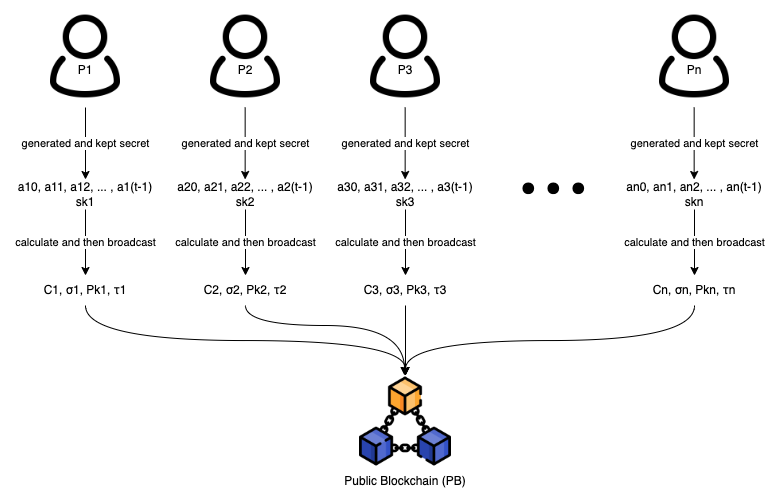
8. Upon receiving the message $(C_i, \; σ_i, \; Pk_i, \; τ_i)$ broadcasted from participant $P_i$, the public blockchain $PB$ verifies $σ_i$ and $τ_i$ by checking as follow:
1. $R_i \;?= \;µ_iG - (H_1(i, Φ, ϕ_{i0}, R_i))ϕ_{i0}$
2. $Ŕ_i \;?= \;ν_iG - (H_2(i, Φ, Pk_i, Ŕ_i))ϕ_{i0}$

If the check passes for all $P_i$, then the first round is considered finished.

On failure, $PB$ mark $P_i$ as malicious for every $(C_i, \; σ_i, \; Pk_i, \; τ_i)$ that fails the verification and then abort the key generation protocol.

### Round 2

1. For $i,j \in \{1,2,3,...,n\}$, each participant $P_i$ computes secret shares for all participants $P_j$ including themselves($P_i$) using their secret polynomial $f_i(x)$.
This can be written explicitly as $P_i \; \xrightarrow{compute} \{f_i(1),f_i(2),f_i(3),...,f_i(n)\}$.
2. Each participant $P_i$ computes a symmetric key $Key_{ij}^{sym} = (sk_i)Pk_j$ for all other $P_j$ where $j \in \{1,2,3,...,n\}$ and $j \neq i$.
This can be written explicitly as $P_i \; \xrightarrow{compute} \{Key_{i1}^{sym},Key_{i2}^{sym},Key_{i3}^{sym},...,Key_{in}^{sym}\}$.
3. Each participant $P_i$ computes an encrypted form of $f_i(j)$ or $e_{ij}$ where $j \in \{1,2,3,...,n\}$ and $j \neq i$ by calculating $e_{ij} = Enc_{sym}(Key_{ij}^{sym}, f_i(j))$.
This can be written explicitly as $P_i \; \xrightarrow{compute} \{e_{i1},e_{i2},e_{i3},...,e_{i(i-1)},e_{i(i+1)},...,e_{in}\}$.
4. Each participant $P_i$ broadcasts $\{e_{ij}|j\in\{1,2,3,...,n\} \; and \; j \neq i\} = \{e_{i1},e_{i2},e_{i3},...,e_{i(i-1)},e_{i(i+1)},...,e_{in}\}$ to $PB$.
This can be written explicitly as $P_i \; \xrightarrow{broadcast \;\; \{e_{i1},e_{i2},e_{i3},...,e_{i(i-1)},e_{i(i+1)},...,e_{in}\}} PB$.
5. After seeing the $e_{ij}$ available on $PB$, each participant $P_j$ computes a symmetric key $Key_{ji}^{sym} = (sk_j)Pk_i$, which is the same as the $Key_{ij}^{sym}$ that $P_i$ used to create $e_{ij}$.
*( $Key_{ji}^{sym}=(sk_j)Pk_i = (sk_j)((sk_i)G)=(sk_i)((sk_j)G)=sk_i(Pk_j)=Key_{ij}^{sym}$ )*
The share $f_i(j)$ can then be derived from the decryption $f_i(j)=Dec_{sym}(Key_{ji}^{sym}, e_{ij})$. The participant $P_j$ then verify the correctness of $f_i(j)$ by checking that $f_i(j)G \; ?= \; \sum_{k=0}^{t-1} j^kϕ_{ik} = ϕ_{i0} + jϕ_{i1} + j^2ϕ_{i2} + ... + j^{t-1}ϕ_{i(t-1)}$.
If the check fail then $P_j$ must complain $P_i$ as follow:

> **Complain(j, i) subprotocol ($P_j$ issues a complaint against $P_i$)**
>
> 1. $P_j$ computes a proof that the $Key_{ji}^{sym}$ is well-formed, which is a proof of knowledge of $sk_j$. To do so, $P_j$ proceeds as follows:
> 1. $P_j$ randomly select a one-time-use nonce $α \in Z_q$
> 2. $P_j$ computes $A_1 = αG$ and $A_2 = αPk_i$
> 3. $P_j$ computes $h = H_3(Pk_j, \; Pk_i,\; Key_{ji}^{sym},\; A_1,\; A_2)$
> 4. $P_j$ computes $z = α + h(sk_j)$
> 5. The proof is $ℼ = (A_1, A_2, z)$
> 6. $P_j$ broadcasts a message $(j,i,Key_{ji}^{sym},ℼ)$ to $PB$ to file a complaint against $P_i$
> 2. $PB$ verifies the proof in $P_j$'s complaint message to determine whether $P_i$ is malicious or not, and if $P_i$ is not malicious, $P_j$ is malicious.
> 1. $PB$ verifies the proof $ℼ$ by checking
> - $A_1 + h(Pk_j) \;?=\; zG$
> - $A_2 + h(Key_{ji}^{sym}) \;?=\; z(Pk_i)$
>
> where $ℼ = (A_1, A_2, z)$ and $h = H_3(Pk_j, \; Pk_i,\; Key_{ji}^{sym},\; A_1,\; A_2)$.
> If the proof is invalid, $P_j$ is marked as malicious, and the key generation protocol is aborted.
>
> 2. $PB$ decrypt $f_i(j)$ by computing $f_i(j) = Dec_{sym}(Key_{ji}^{sym},e_{ij})$.
> 3. $PB$ then verify the correctness of $f_i(j)$ by checking that $f_i(j)G \; ?= \; \sum_{k=0}^{t-1} j^kϕ_{ik} = ϕ_{i0} + jϕ_{i1} + j^2ϕ_{i2} + ... + j^{t-1}ϕ_{i(t-1)}$.
> 4. If the share $f_i(j)$ is correct, mark $P_j$ as malicious, otherwise mark $P_i$ as malicious and abort the key generation protocol.
>
> As a result of this process, it was implied that regardless of who was labeled as malicious, the protocol would be considered aborted if someone complained about someone's misbehavior to the $PB$.
>
6. After having all valid $f_j(i)$ where $j \in \{1,2,3,...,n\}$, each $P_i$ calculates their private signing share or the long-lived secret share $s_i$ by computing $s_i = \sum_{j=1}^{n} f_j(i) = f_1(i)+f_2(i)+f_3(i)+...+f_n(i) = f(i)$, stores $s_i$ locally and securely to only $P_i$.
7. Each $P_i$ broadcast a message to $PB$ to commit that $P_i$ has successfully derive $s_i$. After that the long-lived public key $Y_i$ of $P_i$ can be derive on $PB$ calculating $Y_i = \sum_{j=1}^{n} (\sum_{k=0}^{t-1} i^kϕ_{jk})$
8. After every participants are successfully deriving their long-lived secret keys $\{s_1=f(1),s_2=f(2),s_3=f(3),...,s_n=f(n)\}$ and public key $\{Y_1=s_1G,\;Y_2=s_2G,\;Y_3=s_3G,...,\;Y_n=s_nG\}$, the $PB$ then derive the group's public key $Y$ that can be written as follow:
$Y = \sum_{i=1}^{n}ϕ_{i0} = f(0)G = a_0G = (\sum_{i=1}^{n}a_{i0})G$.
As a result, the above equation also implies that the group’s secret key $s = f(0) = a_0 = \sum_{i=1}^{n}a_{i0}$

## Signing protocol

We assume that a key generation protocol has been successfully completed. Each $P_i$ of the $n$ participants now holds a secret share $s_i = f(i)$, and the group's public key $Y$ is stored on the $PB$. Let $H_1, H_2$ be collision-resistant hash functions with $Z_q$ outputs, and $L_i$ be an on-chain list for $P_i$ to store their commitment shares on the $PB$ due to the preprocessing stage requirement.

### **Preprocessing**

Each participant $P_i$ where $i \in \{1,2,3 . . . , n\}$ performs this stage prior to signing. Let $j$ be a counter for a specific nonce/commitment share pair, and $π$ be the number of pairs generated at a time or the batch size, such that $π$ signing operations can be performed before performing another preprocessing step.

1. Each participant $P_i$ samples or randomly select $π$ pairs of one-time-use nonces $d_{ij},e_{ij} \in Z_q$ where $1 \leq j \leq π$.
2. Derive commitment shares $(D_{ij} , \; E_{ij} ) = (d_{ij}G ,\; e_{ij}G )$.
3. Each participant $P_i$ store all $(d_{ij},e_{ij})$ where $1 \leq j \leq π$, and then broadcasts a new sublist $l_i = [(D_{i1},E_{i1}),(D_{i2},E_{i2}),...,(D_{iπ},E_{iπ})]$ to $PB$. The $PB$ then append $l_i$ to $L_i$ for later use in signing operations.

### Signing

Let $S$ be the set of $t$ participants selected for this signing operation that can be written as

$S =\{x_0,x_1,..,x_{i-1},x_i,x_{i+1},..,x_{t-1}\} \subseteq \{1,2,3,...,n\} \; and \; |S|=t$

, and $Y$ be the group public key. Let $B = ⟨(i, D_i, E_i)⟩_{i∈S}$ denote the ordered or sorted list of participant indices corresponding to each participant $P_i$ , $s_i$ ($P_i$’s secret key share), and $L_i$ be the set of commitment values for $P_i$ that were published during the Preprocess stage where $i \in S$. Each identifier $i$ is coupled with the commitments $(D_i, E_i)$ published by $P_i$ that will be used for this signing operation.

1. After $PB$ receiving a message $m$ that need to be sign, then the following steps will be done on $PB$ in order to initiate the signing process.
1. The set $S$ is selected by the logic implemented on the $PB$
2. After $S$ has been determined, the ordered or sorted list $B = ⟨(i, D_i, E_i)⟩_{i∈S}$ was also constructed on $PB$ for this signing operation.
3. The binding values $ρ_i$ is derived from $ρ_i = H_1(i, m, B)$, $i \in S$, and then derives the group commitment $R = \sum_{i∈S} (D_i + ρ_i(E_i))$ and the challenge $c = H_2(R, Y, m)$.
2. After seeing the group commitment $R$ that has been publish on $PB$, each $P_i$ computes their response using their long-lived secret share $s_i$ by:
1. computing $z_i = d_i + e_iρ_i + λ_is_ic$ using $S$ to determine the $i_{th}$ Lagrange basis polynomial $λ_i(x)$ at $(i_{th},x=0)$ or $λ_i(0) = λ_i = \prod_{j \in S - \{i\}}(\frac{j}{j-i})$
.
2. $P_i$ broadcasts $z_i$ the $PB$.
3. $P_i$ will deletes $(d_i, e_i)$ from their local storage

All response $z_i$ will be used to derive the group’s response $z = \sum_{i \in S} z_i$ on the $PB$.

> **Compatibility with the standard Schnorr signature**

The underlying calculation was done in secret. According to the standard Schnorr signature $σ$ is composed of two components $R = kG, z=k+sc$ where $k$ is a random one-time-use nonce, $s$ is a secret key, and $c=H(R,Y,m)$ where $H$ is a hash function and $m$ is a message to be signed.

The $R = \sum_{i∈S} (D_i + ρ_i(E_i))$ and $z_i = d_i + e_iρ_i + λ_is_ic$ in the group signing process are the same as the standard Schnorr, which can be reasoning as follow:
Let's start with the $R$ component of the group signature.

$R = \sum_{i∈S} (D_i + ρ_i(E_i)) \\~\\
R = \sum_{i∈S} (d_iG + ρ_i(e_iG))
\\~\\
R = (\sum_{i∈S} (d_i + ρ_ie_i))G$

The term $d_i + ρ_ie_i$ can be seen as $k_i$ in the standard Schnorr signature, which $R_i = k_iG = (d_i + ρ_ie_i)G$.
As a result, the group's commitment $R = kG = \sum_{i∈S} R_i = (\sum_{i∈S} k_i)G$ implies that the group's one-time-use nonce $k = \sum_{i∈S} k_i = \sum_{i∈S} (d_i + ρ_ie_i)$ is also compatible with the standard Schnorr signature that $k$ should be a random positive integer within $Z_q$, because $\sum_{i∈S} (d_i + ρ_ie_i)$ is also considered to be a random number within $Z_q$.

The next component of the group signature is $z$.

$z = \sum_{i \in S} z_i \\~\\
z = \sum_{i \in S} (d_i + e_iρ_i + λ_is_ic) \\~\\
z = \sum_{i \in S} (d_i + e_iρ_i) + (\sum_{i \in S} (λ_is_i))c$

Because we already know that $\sum_{i∈S} (d_i + ρ_ie_i) = \sum_{i∈S} k_i = k$, we can continue writing the equation as follows:

$z = \sum_{i \in S} k_i + (\sum_{i \in S} (λ_is_i))c \\~\\
z = k + (\sum_{i \in S} (λ_is_i))c$

The aggregated value $z$ should be the group’s response as in standard Schnorr, which $z = k+sc$. So, the term $\sum_{i \in S} λ_is_i$ must equals to the group’s secret key $s$, which we already know that $s=f(0)$ and $s_i = f(i)$.

To show that $s = \sum_{i \in S} λ_is_i = \sum_{i \in S} λ_if
(i)$, we would have to refer to how a polynomial function of degree $t-1$ can be written as:

$f(x) = a_0 + a_1x + a_1x^2 + ... + a_{t-1}x^{t-1} = \sum_{i=0}^{t-1} λ_i(x)f(x_i) \\~\\
f(0) = a_0 = \sum_{i=0}^{t-1} λ_i(0)f(x_i) = \sum_{i=0}^{t-1} λ_if(x_i) \\~\\
f(0) = \sum_{i=0}^{t-1} λ_if(x_i)$

where $(x_i,f(x_i))$ can be any point in the group’s polynomial $f(x)$ and $λ_i(x)$ is a Lagrange basis polynomial, which in this case can be define as:

$λ_i(x) = \cfrac{(x-x_0)(x-x_1)...(x-x_{i-1})(x-x_{i+1})...(x-x_{t-1})}{(x_i-x_0)(x_i-x_1)...(x_i-x_{i-1})(x_i-x_{i+1})...(x_i-x_{t-1})} \\~\\ where \;\;i \in S = \{x_0,x_1,..,x_{i-1},x_i,x_{i+1},..,x_{t-1}\} \subseteq \{1,2,3,..,n\} \;\;and\;\; |S|=t$

So, the $λ_i(0)$ or $λ_i$ can also be written as:

$λ_i = \cfrac{(0-x_0)(0-x_1)...(0-x_{i-1})(0-x_{i+1})...(0-x_{t-1})}{(x_i-x_0)(x_i-x_1)...(x_i-x_{i-1})(x_i-x_{i+1})...(x_i-x_{t-1})} \\~\\
λ_i = \cfrac{x_0x_1...x_{i-1}x_{i+1}...x_{t-1}}{(x_0-x_i)(x_1-x_i)...(x_{i-1}-x_i)(x_{i+1}-x_i)...(x_{t-1}-x_i)}$

As a result, we can rewrite the $λ_i$ in a more simplified form as follows:
$λ_{i \in S} = \prod_{j \in S-\{i\}}\left(\cfrac{j}{j-i}\right)$
Please also note that the all possible values of the $λ_i$ can be precomputed if the value of $\binom{n}{t}$ is relatively small to the current system. If the size of $\binom{n}{t}$ is too large for the precomputing, it can still be able to compute at runtime once the set $S$ was publish by $PB$.

Since the set $S$ always contains $t$ different indexes $i$ that $i \in \{1,2,3,...,n\}$, we can be confident that the following equation is true.

$z = k + (\sum_{i \in S} (λ_is_i))c \\~\\
z = k + (\sum_{i \in S} λ_if(i))c
\\~\\
z = k + (\sum_{i=0}^{t-1} λ_if(x_i))c
\\~\\
z = k + (f(0))c
\\~\\
z = k + sc$

Because $c=H(R,Y,m)$ and $Y=sG$ where $Y$ is the group's public key, $s$ is the group's secret key, $R$ is the group's commitment, and $m$ is a message to be signed by the group, the group's signature $(R,z)$ produced by this signing process is compatible with the standard Schnorr signature produced by the standard Schnorr process.
>
3. The $PB$ does the following:
1. Upon receiving $z_i$ from participant $P_i$, $i \in S$, verifies the validity of the response by checking $z_iG \; ?= \; R_i + cλ_iY_i$
2. On failure for any $P_i$, the $PB$ mark $P_i$ as malicious and then abort the signing protocol
3. If all responses are correct, computes the group's response $z = \sum_{i \in S} z_i$.
4. $PB$ publish $σ = (R, z)$ as a valid group's signature for message $m$ and terminates the protocol