# Backtracking (9)
> 紀錄 NeetCode-150 與 LeetCode 的解題想法、刷題過程與錯誤,以 Python 或 C++ 兩種語言為主
>
> 其他 NeetCode-150 或 LeetCode 的主題請見 [Here](https://hackmd.io/-ovTFlzLRWaSgzDGhbSwsA)
<!-- 常用色碼紀錄
Easy: <font color="#00ad5f">**Easy**</font>
Medium: <font color="#ffbb00">**Medium**</font>
Hard: <font color="#ee2f56">**Hard**</font>
-->
## Introduction
Backtracking 是一種解題的策略,能夠探索所有可能的選項或路徑,如果無法進行就回溯上一步並嘗試其他可能,持續這個過程直到找到一個最佳解。常用在需要探索多種可能來解決問題的情況,像是迷宮路徑的搜索,或是數獨問題。
Backtracking problem 有以下三種問題類型:
* 可行解問題(decision problem):搜尋一個 feasible solution
* 最佳化問題(optimization problem):搜尋最佳解
* 列舉問題(numeration problem):尋找問題的所有可能的解集合
### Terminologies
* **Candidate**: A candidate is a potential choice or element that can be added to the current solution.
* **Solution**: The solution is a valid and complete configuration that satisfies all problem constraints.
* **Partial Solution**: A partial solution is an intermediate or incomplete configuration being constructed during the backtracking process.
* **Decision Space**: The decision space is the set of all possible candidates or choices at each decision point.
* **Decision Point**: A decision point is a specific step in the algorithm where a candidate is chosen and added to the partial solution.
* **Feasible Solution**: A feasible solution is a partial or complete solution that adheres to all constraints.
* **Dead End**: A dead end occurs when a partial solution cannot be extended without violating constraints.
* **Backtrack**: Backtracking involves undoing previous decisions and returning to a prior decision point.
* **Search Space**: The search space includes all possible combinations of candidates and choices.
* **Optimal Solution**: In optimization problems, the optimal solution is the best possible solution.
### Pseudo code
Backtracking 常見的寫法有兩種模式:
(1) 使用迴圈來歷遍所有元素(see [2. Combination Sum](#2-Combination-Sum))
* 常見在組合(combination)或子集(subset)等類型的題目
* 在每一層會迭代所有選項作為分支,並視情況決定要不要加入(apply)這個分支
* 決定分支後再繼續做遞迴
* 遞迴結束後回溯,將該分支刪除(pop)再繼續下一個選項的分支
```plaintext
void find_solution( parameters):
if (valid solution):
store the solution
Return
for (all choice):
if (valid choice):
Apply(choice)
find_solution(parameters)
backtrack(remove choice)
Return
```
> Note: 可從 [4. Permutations](#4-Permutations) 這題的備註瞭解 for 迴圈做法的內部操作過程
(2) 類似二分法的選擇(see [1. Subsets](#1-Subsets))
* 每個選項可以分為選(pick)或不選(skip)兩個分支
* 選擇某個分支後再往下繼續遞迴
* 此方法會在外部用一個 index 控制當前迭代的哪個元素
```plaintext
void find_solution(parameters):
if (valid solution):
store the solution
Return
Apply(choice)
find_solution(parameters)
backtrack(remove choice)
Not Apply(choice)
```
### Remark
:::info
做 backtracking 的搜索時,通常是用 index 做迭代而不是用陣列本身的元素做迭代,原因有二:
* 能夠動態控制可用選項的範圍
* 避免重複解
:::
### Reference
* [GeeksforGeeks](https://www.geeksforgeeks.org/backtracking-algorithms/)
## 1. Subsets
<font color="#ffbb00">**Medium**</font>
> Given an array `nums` of unique integers, return all possible subsets of `nums`.
>
> The solution set must not contain duplicate subsets. You may return the solution in **any order**.
### Example 1:
```java
Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
```
### Example 2:
```java
Input: nums = [7]
Output: [[],[7]]
```
### Constraints
* `1 <= nums.length <= 10`
* `-10 <= nums[i] <= 10`
### Recommended complexity
* Time complexity: $O(n \cdot 2^n)$
* Space complexity: $O(n)$
### Solution
每個元素可以可以選擇要(pick)或不要(skip),可是用第二種模式進行。
```python=
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
numsLen = len(nums)
res = []
subset = []
def findSolution(index):
# add to result and backtracking
if index >= numsLen:
res.append(subset.copy())
return
# include nums[i] and go next level
subset.append(nums[index])
findSolution(index + 1)
# not include nums[i] and go next level
subset.pop()
findSolution(index + 1)
findSolution(0)
return res
```
:::info
使用 Python 時,因為 list 的值可能會被改變,所以要用 `copy()` 方法把答案複製一份到 `res` 中,避免被修改。
:::
## 2. Combination Sum
<font color="#ffbb00">**Medium**</font>
> You are given an array of **distinct** integers `nums` and a `target` integer target. Your task is to return a list of all **unique combinations** of `nums` where the chosen numbers sum to `target`.
>
> The **same** number may be chosen from `nums` an **unlimited number of times**. Two combinations are the same if the frequency of each of the chosen numbers is the same, otherwise they are different.
>
> You may return the combinations in **any order** and the order of the numbers in each combination can be in **any order**.
### Example 1:
```java
Input:
nums = [2,5,6,9]
target = 9
Output: [[2,2,5],[9]]
```
Explanation:
2 + 2 + 5 = 9. We use 2 twice, and 5 once.
9 = 9. We use 9 once.
### Example 2:
```java
Input:
nums = [3,4,5]
target = 16
Output: [[3,3,3,3,4],[3,3,5,5],[4,4,4,4],[3,4,4,5]]
```
### Example 3:
```java
Input:
nums = [3]
target = 5
Output: []
```
### Constraints:
* All elements of `nums` are **distinct**.
* `1 <= nums.length <= 20`
* `2 <= nums[i] <= 30`
* `2 <= target <= 30`
### Recommended complexity
* Time complexity: $O(2^{\frac{t}{m}})$
* Space complexity: $O(\frac{t}{m})$
### Solution
此題重點在於什麼時候要停止搜索下一層?
* 超過 target value 時回溯
* 等於 target value 時回溯
其餘寫法如同正規的 backtracking 步驟,可用第一種模式歷遍所有可能的分支與組合。
```python=
class Solution:
def combinationSum(self, nums: List[int], target: int) -> List[List[int]]:
res = []
n = len(nums)
def backtrack(startIdx, path, currSum):
if currSum == target:
res.append(path.copy())
return
if currSum > target:
return
for i in range(startIdx, n):
path.append(nums[i]) # apply(choice)
totalSum = currSum + nums[i] # apply(choice)
backtrack(i, path, totalSum) # next layer
path.pop() # backtrack and perform next branch
backtrack(0, [], 0)
return res
```
## 3. Combination Sum ll
<font color="#ffbb00">**Medium**</font>
> You are given an array of integers `candidates`, which may contain duplicates, and a target integer `target`. Your task is to return a list of all **unique combinations** of `candidates` where the chosen numbers sum to `target`.
>
> Each element from `candidates` may be chosen **at most once** within a combination. The solution set must not contain duplicate combinations.
>
> You may return the combinations in **any order** and the order of the numbers in each combination can be in **any order**.
### Example 1:
```java
Input: candidates = [9,2,2,4,6,1,5], target = 8
Output: [
[1,2,5],
[2,2,4],
[2,6]
]
```
### Example 2:
```java
Input: candidates = [1,2,3,4,5], target = 7
Output: [
[1,2,4],
[2,5],
[3,4]
]
```
### Constraints
* `1 <= candidates.length <= 100`
* `1 <= candidates[i] <= 50`
* `1 <= target <= 30`
### Recommended complexity
* Time complexity: $O(n \cdot 2^n)$
* Space complexity: $O(n)$
### Solution
最大的問題是輸入陣列有重複元素,所以在 for 迴圈歷遍同層所有分支時,可能會產生重複解,如下圖所示

解決方法如下:
* 先對輸入陣列排序
* 每層從最小值開始歷遍所有分支時,如果遇到跟前一個分支元素相同就跳過
:::info
**Remark 1**
所謂的跳過,指的是直接跳過該次迴圈,不是只跳過該分支,如果只跳過該分支,使用 `i+1` 作為下一次的 `startIdx`,則下一次的迴圈可能會重複執行下一個分支。
以 `sortedInputArray = [1, 2, 2*, 4, 5, 6, 9]` 為例,當迴圈執行到 `2*` 分支時,因為跟前一個元素相同,所以跳下一個元素 `4`,此時如果單純跳過該元素執行 `i+1`(即 `4`) 作為下一個分支往下搜索,則下一次的迴圈還會再用 `4` 作為分支一次,結果就會有重複。
正確做法應該是使用 `continue` 直接略過該次迴圈。
**Remark 2**
檢查停止條件時,只要檢查 `currentSum > target` 即可,不用再檢查起始點有沒有超過陣列長度(`startIdx >= n`),因為在 Python 中如果起始點超過結束點,就不會進入到迴圈中。
:::
```python=
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
res = []
n = len(candidates)
currentSum = 0
path = []
def dfs(startIdx, path, currentSum):
if currentSum == target:
res.append(path.copy())
return
if currentSum >= target:
return
for i in range(startIdx, n):
if i > startIdx and candidates[i] == candidates[i - 1]:
continue
path.append(candidates[i])
dfs(i + 1, path, currentSum + candidates[i])
path.pop()
dfs(0, path, currentSum)
return res
```
## 4. Permutations
<font color="#ffbb00">**Medium**</font>
> Given an array `nums` of **unique** integers, return all the possible permutations. You may return the answer in **any order**.
### Example 1:
```java
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
```
### Example 2:
```java
Input: nums = [7]
Output: [[7]]
```
### Constraints
* `1 <= nums.length <= 6`
* `-10 <= nums[i] <= 10`
### Recommended complexity
* Time complexity: $O(n \cdot n!)$
* Space omplexity: $O(n)$
### Solution
在使用樹狀圖遞迴排列的過程中,每一次往下搜索的遞迴都可以加入(append)一個元素,但前提是加入的元素必須要是沒被使用過的。所以可以使用一個陣列來紀錄哪些元素在選擇分支的迭代過程中有被使用過。被使用過就跳過,沒被使用過就可以加入。
何時結束搜索?當元素排列的長度 = 輸入陣列長度時,代表所有元素都使用過,此時停止搜索並回溯上一層。
```python=
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
n = len(nums)
path = []
used = [False] * n
def backtrack(path, used):
if len(path) == n:
res.append(path.copy())
return
for i in range(n):
if used[i]:
continue
else:
path.append(nums[i]) # apply choice
used[i] = True # apply choice
backtrack(path, used) # next layer
path.pop() # backtrack
used[i] = False # backtrack
backtrack(path, used)
return res
```
:::info
依照程式碼的整個搜索過程如下圖所示,可從此圖瞭解 backtracking 問題中典型的 for 迴圈做法的內部操作過程。

:::
## 5. Subset ll
<font color="#ffbb00">**Medium**</font>
> You are given an array `nums` of integers, which may contain duplicates. Return all possible subsets.
>
> The solution must not contain duplicate subsets. You may return the solution in **any order**.
### Example 1:
```java
Input: nums = [1,2,1]
Output: [[],[1],[1,2],[1,1],[1,2,1],[2]]
```
### Example 2:
```java
Input: nums = [7,7]
Output: [[],[7], [7,7]]
```
### Constraints
* `1 <= nums.length <= 11`
* `-20 <= nums[i] <= 20`
### Recommended complexity
* Time complexity: $O(n \cdot 2^n)$
* Space complexity: $O(n)$
### Solution
* for 迴圈的典型寫法中,將解答加入選項的動作應該在迴圈外部進行
* 與 [Combination Sum ll](#Combination-Sum-ll) 類似的解題策略
* Subset 中的元素可以重複,但 subset 本身不能重複,將輸入陣列先進行排序可以避免在同一層中選到重複解
* 遞迴過程中遇到重複元素時只做 `i = i + 1` 只是跳過重複元素並執行重複元素的下一個,但下一次的迴圈可能又會再次執行這個(重複後的下一個)元素
* 正確做法應該是直接跳過該次迴圈,什麼都不做
* 起始編號 `startIdx` 不用刻意檢查 `startIdx >= n`,因為如果超過了就不會進入迴圈
```python=
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
nums.sort()
n = len(nums)
subset = []
startIdx = 0
def backtrack(subset, startIdx):
res.append(subset.copy())
# if startIdx >= n:
# return
for i in range(startIdx, n):
#--------------------------------------------#
# res.append(subset.copy())
# apply choice 寫在迴圈內部會造成 subset 重複添加
# 因為一開始進入迴圈會先 append 一次
# 迴圈結束前把新增元素從 subset 刪除後,下一個迴圈會再 append 一次
# 所以 apply choice 應該放在迴圈外部(進入迴圈前)
#--------------------------------------------#
if i > startIdx and nums[i] == nums[i-1]:
# i += 1 應該直接跳過該次迴圈,不是跳過該元素
continue
subset.append(nums[i])
backtrack(subset, i+1)
subset.pop()
backtrack(subset, startIdx)
return res
```
## 6. Word Search
<font color="#ffbb00">**Medium**</font>
> Given a 2-D grid of characters `board` and a string `word`, return `true` if the word is present in the grid, otherwise return `false`.
>
> For the word to be present it must be possible to form it with a path in the board with horizontally or vertically neighboring cells. The same cell may not be used more than once in a word.
### Example 1:
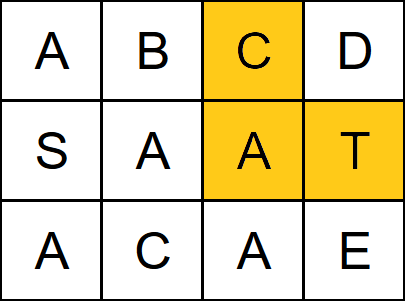
```java
Input:
board = [
["A","B","C","D"],
["S","A","A","T"],
["A","C","A","E"]
],
word = "CAT"
Output: true
```
### Example 2:
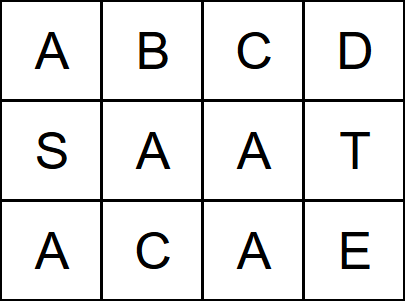
```java
Input:
board = [
["A","B","C","D"],
["S","A","A","T"],
["A","C","A","E"]
],
word = "BAT"
Output: false
```
### Constraints
* `1 <= board.length, board[i].length <= 5`
* `1 <= word.length <= 10`
* `board` and `word` consists of only lowercase and uppercase English letters.
### Recommended complexity
* Time complexity: $O(m \codt (4^n))$
* `m` is the number of cells in the given `board`
* `n` is the size of the given `word`
* Space complexity: $O(n)$
### Solution
* 使用一個 hash set 來儲存走過的路徑
* 同樣使用一個外部變數來控制 `word` 的迭代狀況
* base condition
* `board` 的邊界
* `ward` 的匹配
* 是否走過該路徑
整體有點類似 for loop 的變形,但因為每個位置都只有 4 個選擇(i.e., branch = 4),所以不是用 for loop 的方式呈現,是直接 4 個狀況都走過一次。
```pytohn=
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
ROWS, COLS = len(board), len(board[0])
path = set() # save traversal path
def backtrack(row, col, path, startIdx):
if startIdx == len(word):
return True
if (row >= ROWS or col >= COLS or
row < 0 or col < 0 or
board[row][col] != word[startIdx] or
(row, col) in path):
return False
path.add((row, col))
res = (backtrack(row+1, col, path, startIdx+1) or
backtrack(row-1, col, path, startIdx+1) or
backtrack(row, col+1, path, startIdx+1) or
backtrack(row, col-1, path, startIdx+1))
path.remove((row, col))
return res
for r in range(ROWS):
for c in range(COLS):
if backtrack(r, c, path, 0):
return True
return False
```
## 7. Palindrome Partitioning
<font color="#ffbb00">**Medium**</font>
> Given a string `s`, split `s` into substrings where every substring is a palindrome. Return all possible lists of palindromic substrings.
>
> You may return the solution in **any order**.
### Example 1:
```java
Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]
```
### Example 2:
```java
Input: s = "a"
Output: [["a"]]
```
### Constraints
* `1 <= s.length <= 20`
* `s` contains only lowercase English letters.
### Recommended complexity
* Time complexity: $O(n \cdot (2^n))$
* `n` is the length of the input string
* Space complexity: $O(n)$
### Solution
類似找子集的方式,每個位置元素都可以選擇繼續 append 或是從此處開始分開找下一個回文,如下圖所示

判斷回文可以用 two pointer 的方式,所以每次檢查時使用兩個變數 `start` 與 `end` 判斷是否為回文字,以及要 appene 或斷開
* 如果選擇繼續 append,則 backtrack 遞迴時就繼續搜尋 `end + 1`
* 如果選擇分開找下一段,則迴圈繼續搜索 `start = start + 1`
* 當起始指標超過字串長度時搜索結束(base condition)
```pytohn=
class Solution:
def partition(self, s: str) -> List[List[str]]:
res = []
n = len(s)
def backtrack(path, startIdx):
if startIdx >= n:
res.append(path.copy())
return
for end in range(startIdx, n):
if self.isPalindrome(s, startIdx, end):
path.append(s[startIdx:end+1])
backtrack(path, end+1)
path.pop() # included in if structure since it must follow backtrack()
backtrack([], 0)
return res
def isPalindrome(self, s, LP, RP):
while (LP < RP):
if s[LP] == s[RP]:
LP += 1
RP -= 1
else:
return False
return True
```
## 8. Letter Combinations of a Phone Number
<font color="#ffbb00">**Medium**</font>
> You are given a string `digits` made up of digits from `2` through `9` inclusive.
>
> Each digit (not including 1) is mapped to a set of characters as shown below:
>
> A digit could represent any one of the characters it maps to.
>
> Return all possible letter combinations that `digits` could represent. You may return the answer in **any order**.

### Example 1:
```java
Input: digits = "34"
Output: ["dg","dh","di","eg","eh","ei","fg","fh","fi"]
```
### Example 2:
```java
Input: digits = ""
Output: []
```
### Constraints
* `0 <= digits.length <= 4`
* `2 <= digits[i] <= 9`
### Recommended complexity
* Time complexity: $O(n \cdot (4^n))$
* `n` is the length of the input string
* Space comlexity: $O(n)$
### Solution
題目沒有給數字對應的英文字母,所以要自建 hash map 來做對照,但因爲長度固定,所以不算記憶體空間。
同樣使用一個外部變數來控制`digits` 的數字,且因為每個數字會對應到多個字母,所以看起來「似乎」要用兩個外部變數來控制迴圈,外層控制 `digits` 的數字,內層控制數字對應的字母。
但實際上外層 `digits` 數字如果用迴圈歷遍所有數,會造成答案重複(如答案的註解)。正確做法應該是外層用控制變數歷遍,內層字母才用迴圈控制。
停止條件:當 digits 到達結尾時停止
```python=
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
if not digits:
return []
digitToAlphabet = {
'2':"abc",
'3':"def",
'4':"ghi",
'5':"jkl",
'6':"mno",
'7':"pqrs",
'8':"tuv",
'9':"wxyz"
}
res = []
digitLen = len(digits)
def backtrack(path, startIdx):
if startIdx >= digitLen:
res.append(path)
return
d = digits[startIdx]
for ch in digitToAlphabet[d]:
backtrack(path+ch, startIdx+1)
# 此方法的外層迴圈會重複歷遍所有數字(Ex: digits="34")
# i = 0 時選擇第一個數字 3
# 選擇字母 d -> backtrack(d, 1)
# i = 1 時選擇第二個數字 4
# 選擇字母 g -> backtrack(dg, 2) -> res = [dg]
# ...
# 選擇字母 e -> backtrack(e, 1)
# i = 1 時選擇第二個數字 4
# 選擇字母 g -> backtrack(eg, 2) -> res = [eg]
# ...
# ...
# i = 1 時選擇第二個數字 4(重複)
# 選擇字母 g -> backtrack(g, 2)
# 正確做法是移除外層迴圈
# for i in range(startIdx, digitLen):
# for ch in digitToAlphabet[digits[i]]:
# backtrack(path+ch, startIdx+1)
backtrack("", 0)
return res
```
## 9. N-Queens
<font color="#ee2f56">**Hard**</font>
> The **n-queens** puzzle is the problem of placing `n` queens on an `n x n` chessboard so that no two queens can attack each other.
>
> A **queen** in a chessboard can attack horizontally, vertically, and diagonally.
>
> Given an integer `n`, return all distinct solutions to the **n-queens puzzle**.
>
> Each solution contains a unique board layout where the queen pieces are placed. `'Q'` indicates a queen and `'.'` indicates an empty space.
>
> You may return the answer in **any order**.
### Example 1:
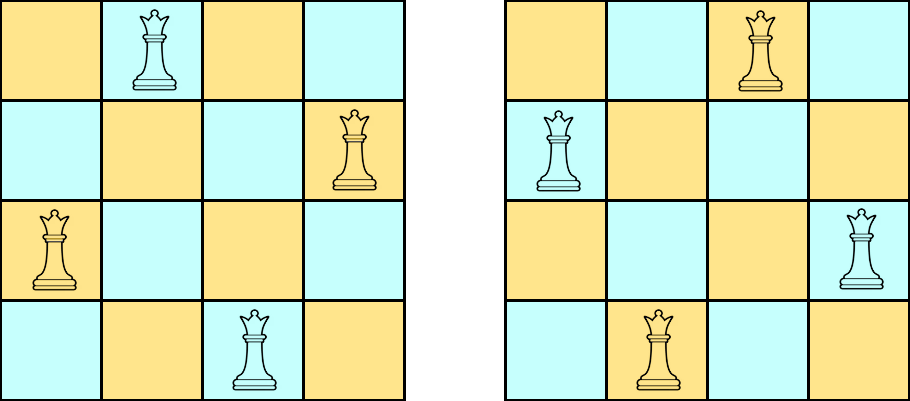
```java
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
```
Explanation: There are two different solutions to the 4-queens puzzle.
### Example 2:
```java
Input: n = 1
Output: [["Q"]]
```
### Constraints
* `1 <= n <= 8`
### Recommended complexity
* Time complexity: $O(n!)$
* `n` is the size of the given square board
* Space complexity: $O(n^2)$
### Solution
每個 queen 有 8 的方向(上、下、左、右、左上、左下、右上、右下)可以走。
(1) 以上下左右的方位來看:任兩個 queen 不能在同行或同列
* 以行(或列也可,擇一)為主作迭代,每一行都只能放一個 queen
* 且同時確保任兩個 queen 不在同列(迴圈)
* 每個列都去迭代所有的行
(2) 左上、右下、左下、右上 4 個方位:可以使用斜率判斷
* slope > 0 的對角線上,每個點的位置的 row 與 col 座標相加都相等
* slope < 0 的對角線上,每個點的位置的 row 與 col 座標相減都相等

(3) 使用三個 hash set:COL, posDiag, negDiag 來記錄走過的路徑
* 當所有 row 都走完,則返回上一部
```python=
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
res = []
COLS = set() # from 0 to n-1
posDiag = set() # row + col
negDiag = set() # row - col
board = [['.'] * n for i in range(n)]
def backtrack(row):
if row == n:
copy = ["".join(r) for r in board]
res.append(copy)
return
for col in range(n):
if (col in COLS or
(row + col) in posDiag or
(row - col) in negDiag):
continue
# apply solution
COLS.add(col)
posDiag.add(row + col)
negDiag.add(row - col)
board[row][col] = 'Q'
backtrack(row + 1)
# backtrack
COLS.remove(col)
posDiag.remove(row + col)
negDiag.remove(row - col)
board[row][col] = '.'
backtrack(0)
return res
```