Pipelining - HackMD

<style> .reveal { font-size: 24px; } .reveal section img { background:none; border:none; box-shadow:none; } pre.graphviz { box-shadow: none; } </style> # Pipelining *(AMH chapters 3-5, 11.1)* Performance Engineering, Lecture 2 Sergey Slotin May 7, 2022 --- ## CPU pipeline To execute *any* instruction, processors need to do a lot of preparatory work first: - **fetch** a chunk of machine code from memory - **decode** it and split it into instructions - **execute** these instructions (which may involve doing some **memory** operations) - **write** the results back into registers This whole sequence of operations takes up to 15-20 CPU cycles even for something simple like `add`-ing two register-stored values together ---- To hide this latency, modern CPUs use *pipelining*: after an instruction passes through the first stage, they start processing the next one right away, without waiting for the previous one to fully complete ![](https://en.algorithmica.org/hpc/pipelining/img/pipeline.png) 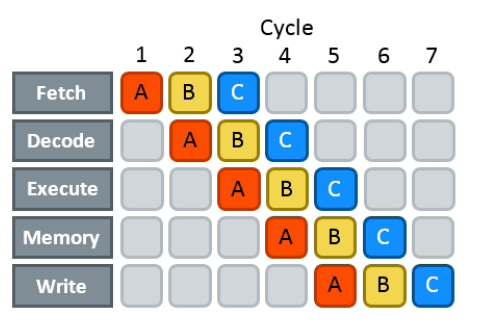Pipelining does not reduce *actual* latency but makes it seem like if it was composed of only the execution and memory stage ---- ![](https://media.ford.com/content/fordmedia/fna/us/en/features/game-changer--100th-anniversary-of-the-moving-assembly-line.img.png/1500004048707.jpg =600x) Real-world analogue: Henry Ford's assembly line ---- - To control for clock frequenccy, processor microarchitectures are benchmarked in terms of *cycles per instruction* (CPI) - A perfectly pipelined CPU keeps every stage busy with some instruction, so that $\text{# of instructions} \to \infty,\; CPI \to 1$ - **Superscalar** processors have more than one of everything, in which case CPI could be less than 1  - The processor maintains a queue of pending instructions and starts executing them as soon as they are ready (*out-of-order execution*)  --- ## Hazards *Pipeline hazards* are situations when the next instruction can't execute on the following clock cycle, causing a pipeline stall or "bubble" ![](https://simplecore-ger.intel.com/techdecoded/wp-content/uploads/sites/11/figure-6-3.png =350x) - *Structural hazard*: two or more instructions need the same part of CPU - *Data hazard*: need to wait for operands to be computed from a previous step - *Control hazard*: the CPU can't tell which instructions it needs to execute next ---- - In *structural hazards*, you have to wait (usually one cycle) until the execution unit is ready; they are fundamental bottlenecks on performance and can’t be avoided - In *data hazards*, you have to wait for the data to be computed (the latency of the critical path); data hazards are solved by shortening the critical pathr - In *control hazards*, you have to flush the entire pipeline and start over, wasting 15-20 cycles; they are solved by removing branches or making them predictable so that the CPU can successfully *speculate* on what is going to be executed next --- ## The Cost of Branching Let's simulate a completely unpredictable branch ```cpp const int N = 1e6; int a[N]; for (int i = 0; i < N; i++) a[i] = rand() % 100; // this part is benchmarked: volatile int s; // to prevent vectorization, iteration interleaving, or other "cheating" for (int i = 0; i < N; i++) if (a[i] < 50) s += a[i]; ``` Measures ~14 CPU cycles per element ---- ```nasm mov rcx, -4000000 jmp body counter: add rcx, 4 jz finished ; "jump if rcx became zero" body: mov edx, dword ptr [rcx + a + 4000000] cmp edx, 49 jg counter add dword ptr [rsp + 12], edx jmp counter ``` On a mispredict, we need to discard the pipeline (~19 cycles), perform a fetch and comparison (~5), per pipeline discard, and add `a[i]` to a volatile variable in case of a `<` branch (~4), bringing the expected value to roughly $(4 + 5 + 19) / 2 = 14$ ---- Add a tweakable parameter `P`: ```cpp for (int i = 0; i < N; i++) if (a[i] < P) s += a[i]; ``` It sets the branch probability ---- ![](https://en.algorithmica.org/hpc/pipelining/img/probabilities.svg =500x) ---- - Most of the time, to do branch prediction, the CPU only needs a hardware statistics counter: if we historically took branch A more often than not, then it is probably more likely to be taken next - Modern branch predictors are much smarter than that and can detect more complicated patterns ---- ```cpp for (int i = 0; i < N; i++) a[i] = rand() % 100; std::sort(a, a + n); ``` It runs 3.5x faster: using slightly over 4 cycles per element (the average of the cost of pure `<` and `>=`) ---- ```cpp const int N = 1000; // ... ``` Small arrays also at ~4 (it memorizes the entire array) ---- ### Hinting likeliness A new C++ feature: ```cpp for (int i = 0; i < N; i++) if (a[i] < P) [[likely]] s += a[i]; ``` When $P = 75$, it measures around ~7.3 cycles per element, while the original version without the hint needs ~8.3 ---- Without hint: ```nasm loop: ; ... cmp edx, 49 jg loop add dword ptr [rsp + 12], edx jmp loop ``` With hint: ```nasm body: ; ... cmp edx, 49 jg loop add dword ptr [rsp + 12], edx loop: ; ... jmp body ``` General idea: we want to have access to the next instructions as soon as possible --- ## Predication The best way to deal with branches is to remove them, which we can do with *predication*, roughly equivalent to this algebraic trick: $$ x = c \cdot a + (1 - c) \cdot b $$ We eliminate control hazards at the cost of evaluating *both* branches (and somehow "joining" them) ---- It takes ~7 cycles per element instead of the original ~14: ```cpp for (int i = 0; i < N; i++) s += (a[i] < 50) * a[i]; ``` What does `(a[i] < 50) * a[i]` even do? There are no booleans in assembly ```nasm mov ebx, eax ; t = x sub ebx, 50 ; t -= 50 (underflow if x < 50, setting highest bit to 1) sar ebx, 31 ; t >>= 31 imul eax, ebx ; x *= t ```  ---- `((a[i] - 50) >> 31 - 1) & a[i]` ```nasm mov ebx, eax ; t = x sub ebx, 50 ; t -= 50 sar ebx, 31 ; t >>= 31 ; imul eax, ebx ; x *= t sub ebx, 1 ; t -= 1 (underflow if t = 0) and eax, ebx ; x &= t (either 0 or all 1s) ``` This makes the whole sequence one cycle faster (`imul` took 3 cycles, `sub` + `and` takes 2) ---- ### Conditional move Instead of arithmetic tricks, Clang uses a special `cmov` (“conditional move”) instruction that assigns a value based on a condition: ```nasm mov ebx, 0 ; cmov doesn't support immediate values, so we need a zero register cmp eax, 50 cmovge eax, ebx ; eax = (eax >= 50 ? eax : ebx=0) ``` The original code is actually closer to: ```cpp for (int i = 0; i < N; i++) s += (a[i] < 50 ? a[i] : 0); ``` ---- ![](https://en.algorithmica.org/hpc/pipelining/img/branchy-vs-branchless.svg =500x) 75% is a commonly used heuristic in compilers ---- ### Larger examples - Zero strings - Binary searching - Data-parallel programming ```cpp /* volatile */ int s = 0; for (int i = 0; i < N; i++) if (a[i] < 50) s += a[i]; ```  --- ## Latency and Throughput | Instruction | Latency | RThroughput | |-------------|---------|:------------| | `jmp` | - | 2 | | `mov r, r` | - | 1/4 | | `mov r, m` | 4 | 1/2 | | `mov m, r` | 3 | 1 | | `add` | 1 | 1/3 | | `cmp` | 1 | 1/4 | | `popcnt` | 1 | 1/4 | | `mul` | 3 | 1 | | `div` | 13-28 | 13-28 | Zen 2 instruction tables https://www.agner.org/optimize/instruction_tables.pdf ---- ![](https://uops.info/pipeline.png =400x) https://uops.info ---- For example, in Sandy Bridge family there are 6 execution ports: * Ports 0, 1, 5 are for arithmetic and logic operations (ALU) * Ports 2, 3 are for memory reads * Port 4 is for memory write You can lookup them up in instruction tables and find out which one is the bottleneck ---- Optimizing for latency is usually quite different from optimizing for throughput. - Optimizing for latency, you need to make dependency chains shorter - Optimizing for throughput, you need to remove pressure from bottlenecks Nothing about "sum up all operations weighted by their costs" but throughput computing is ideologically somewhat closer to it ---- ```cpp int s = 0; for (int i = 0; i < n; i++) s += a[i]; ``` (Pretend vectorization doesn't exist) ---- ```cpp int s = 0; s += a[0]; s += a[1]; s += a[2]; s += a[3]; // ... ``` The next iteration depends on the previous one, so we can't execute more than one iteration per cycle despite `mov`/`add` having a throughput of two ---- ```cpp int s0 = 0, s1 = 0; s0 += a[0]; s1 += a[1]; s0 += a[2]; s1 += a[3]; // ... int s = s0 + s1; ``` We can now proceed in two concurrent "threads", doubling the throughput --- ## Profiling 1. Instrumentation  2. Statistical profiling  3. Simulation  ---- ## Perf --- ## Case study: GCD Euclid's algorithm finds the *greatest common divisor* (GCD): $$ \gcd(a, b) = \max_{g: \; g|a \, \land \, g | b} g $$ The algorithm recursively applies the formula and eventually converges to $b = 0$: $$ \gcd(a, b) = \begin{cases} a, & b = 0 \\ \gcd(b, a \bmod b), & b > 0 \end{cases} $$ Works because if $g = \gcd(a, b)$ divides both $a$ and $b$, it should also divide $(a \bmod b = a - k \cdot b)$, but any larger divisor $d$ of $b$ will not ---- For random numbers under $10^9$, the average # of iterations is around 20 and the max is achieved for 433494437 and 701408733, the 43rd and 44th Fibonacci numbers ![](https://en.algorithmica.org/hpc/algorithms/img/euclid.svg =500x) You can see bright blue lines at the proportions of the golden ratio ---- ```cpp int gcd(int a, int b) { if (b == 0) return a; else return gcd(b, a % b); } ``` ```cpp int gcd(int a, int b) { return (b ? gcd(b, a % b) : a); } ```  ```cpp int gcd(int a, int b) { while (b > 0) { a %= b; std::swap(a, b); } return a; } ```  ```cpp int gcd(int a, int b) { while (b) b ^= a ^= b ^= a %= b; return a; } ```  ^Not even UB since C++17!  ---- ```nasm ; a = eax, b = edx loop: ; modulo in assembly: mov r8d, edx cdq idiv r8d mov eax, r8d ; (a and b are already swapped now) ; continue until b is zero: test edx, edx jne loop ``` `perf` says it spends ~90% of the time on the `idiv` line: general integer division is slow ---- ### Division by constants When we divide one floating number $x$ by constant $y$, we can pre-calculate $$ d \approx y^{-1} $$ and then, during runtime, calculate $$ x / y = x \cdot y^{-1} \approx x \cdot d $$ This trick can be extended to integers:  ```cpp ; input (rdi): x ; output (rax): x mod (m=1e9+7) mov rax, rdi movabs rdx, -8543223828751151131 ; load magic constant into a register mul rdx ; perform multiplication mov rax, rdx shr rax, 29 ; binary shift of the result ```  But general division is slow,  **unless this is a divsion by two**  ---- ### Binary GCD 1. $\gcd(0, b) = b$ (and symmetrically $\gcd(a, 0) = a$) 3. $\gcd(2a, 2b) = 2 \cdot \gcd(a, b)$ 4. $\gcd(2a, b) = \gcd(a, b)$ if $b$ is odd (and symmetrically $\gcd(a, b) = \gcd(a, 2b)$ if $a$ is odd) 6. $\gcd(a, b) = \gcd(|a − b|, \min(a, b))$, if $a$ and $b$ are both odd $O(\log n)$: one of the arguments is divided by 2 at least every two iterations  This algorithm is interesting because there is no division: the only arithmetic operations we need are binary shifts, comparisons, and subtractions — all taking just one cycle  ---- ```cpp int gcd(int a, int b) { // base cases (1) if (a == 0) return b; if (b == 0) return a; if (a == b) return a; if (a % 2 == 0) { if (b % 2 == 0) // a is even, b is even (2) return 2 * gcd(a / 2, b / 2); else // a is even, b is odd (3) return gcd(a / 2, b); } else { if (b % 2 == 0) // a is odd, b is even (3) return gcd(a, b / 2); else // a is odd, b is odd (4) return gcd(std::abs(a - b), std::min(a, b)); } } ``` Two times **slower** than `std::gcd`, mainly due to all the branching and case matching 1. Replace all divisions by 2 with division by whichever highest power of 2 we can. This can be done with `__builtin_ctz` ("count trailing zeros"). Expected to decrease the number of iterations by almost a factor 2 because  $1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots \to 2$ 2. Condition 2 can now only be true once: in the very beginning  3. After we've entered condition 4 and applied its identity, $a$ will always be even and $b$ will always be odd, so we will be in condition 3. We can "de-evenize" $a$ right away and thus only loop from 4 to 3 until terminating by condition 1  ---- ```cpp int gcd(int a, int b) { if (a == 0) return b; if (b == 0) return a; int az = __builtin_ctz(a); int bz = __builtin_ctz(b); int shift = std::min(az, bz); a >>= az, b >>= bz; while (a != 0) { int diff = a - b; b = std::min(a, b); a = std::abs(diff); a >>= __builtin_ctz(a); } return b << shift; } ``` It runs in 116ns, while `std::gcd` takes 198ns ---- ```nasm ; a = edx, b = eax loop: mov ecx, edx sub ecx, eax ; diff = a - b cmp eax, edx cmovg eax, edx ; b = min(a, b) mov edx, ecx neg edx cmovs edx, ecx ; a = max(diff, -diff) = abs(diff) tzcnt ecx, edx ; az = __builtin_ctz(a) sarx edx, edx, ecx ; a >>= az test edx, edx ; a != 0? jne loop ``` ---- Total time ~ length of dependency chain ![](https://en.algorithmica.org/hpc/algorithms/img/gcd-dependency1.png =250x) We can calculate `ctz` using just `diff = a - b` because a negative number divisible by $2^k$ still has $k$ zeros at the end  ---- ![](https://en.algorithmica.org/hpc/algorithms/img/gcd-dependency2.png =350x) ---- ```cpp int gcd(int a, int b) { if (a == 0) return b; if (b == 0) return a; int az = __builtin_ctz(a); int bz = __builtin_ctz(b); int shift = std::min(az, bz); b >>= bz; while (a != 0) { a >>= az; int diff = b - a; az = __builtin_ctz(diff); b = std::min(a, b); a = std::abs(diff); } return b << shift; } ``` 198ns → 116ns → 91ns. Our job here is done