<style> .reveal { font-size: 24px; } .reveal section img { background:none; border:none; box-shadow:none; } pre.graphviz { box-shadow: none; } </style> # SIMD Parallelism *(AMH chapters 10-11)* Performance Engineering, Lecture 3 Sergey Slotin May 7, 2022 --- ```cpp const int n = 1e5; int a[n], s = 0; int main() { for (int t = 0; t < 100000; t++) for (int i = 0; i < n; i++) s += a[i]; return 0; } ``` If we compile it with plain `g++ -O3` and run, it finishes in 2.43 seconds ---- ```cpp #pragma GCC target("avx2") // (the rest is the same) const int n = 1e5; int a[n], s = 0; int main() { for (int t = 0; t < 100000; t++) for (int i = 0; i < n; i++) s += a[i]; return 0; } ``` 1.24 seconds — twice as fast (!) --- ## Single Instruction, Multple Data  Instructions that perform the same operation on multiple data points (blocks of 128, 256 or 512 bits, also called *vectors*) ----  Backwards-compatible up until AVX-512 (x86-specific, but ARM NEON and GPUs are very similar) <!-- .element: class="fragment" data-fragment-index="1" --> If you don't have access to SIMD in *some* form in 2022, you are either a front-end developer or programming a microwave <!-- .element: class="fragment" data-fragment-index="2" --> ---- You can check compatibility during runtime: ```cpp cout << __builtin_cpu_supports("sse") << endl; cout << __builtin_cpu_supports("sse2") << endl; cout << __builtin_cpu_supports("avx") << endl; cout << __builtin_cpu_supports("avx2") << endl; cout << __builtin_cpu_supports("avx512f") << endl; ``` ...or call `cat /proc/cpuinfo` and see CPU flags along with other info --- ## How to Use SIMD Converting a program from scalar to vector one is called *vectorization*, which can be achieved using a combination of: * x86 assembly * **C/C++ intrinsics** * **Vector types** * SIMD libraries * Auto-vectorization Later are simpler, former are more flexible ---- ### Intel Intrinsics Guide  Nobody likes writing raw assembly https://software.intel.com/sites/landingpage/IntrinsicsGuide/ ---- All C++ intrinsics can be included with `x86intrin.h` ```cpp #pragma GCC target("avx2") #pragma GCC optimize("O3") #include <x86intrin.h> #include <bits/stdc++.h> using namespace std; ``` You can also drop pragmas and compile with `-O3` and `-march=native` or `-mavx2` ---- ```cpp double a[100], b[100], c[100]; // iterate in blocks of 4, // because that's how many doubles can fit into a 256-bit register for (int i = 0; i < 100; i += 4) { // load two 256-bit segments into registers __m256d x = _mm256_loadu_pd(&a[i]); __m256d y = _mm256_loadu_pd(&b[i]); // add 4+4 64-bit numbers together __m256d z = _mm256_add_pd(x, y); // write the 256-bit result into memory, starting with c[i] _mm256_storeu_pd(&c[i], z); } ``` ---- ## SIMD Registers - SSE (1999) added 16 128-bit registers called `xmm0` through `xmm15` - AVX (2011) added 16 256-bit registers called `ymm0` through `ymm15` - AVX512 (2017) added 16 512-bit registers called `zmm0` through `zmm15` (plus a bunch of "mask" registers) ---- - 128-bit `__m128`, `__m128d` and `__m128i` types for single-precision floating-point, double-precision floating-point and various integer data respectively - 256-bit `__m256`, `__m256d`, `__m256i` - 512-bit `__m512`, `__m512d`, `__m512i` You can freely convert between them with C-style casting ---- ### SIMD Instructions Most SIMD intrinsics follow a naming convention similar to `_mm<size>_<action>_<type>` and correspond to a single analogously named assembly instruction - `_mm_add_epi16`: add two 128-bit vectors of 16-bit *extended packed integers*, or simply said, `short`s - `_mm256_acos_pd`: calculate elementwise $\arccos$ for 4 *packed doubles* - `_mm256_broadcast_sd`: broadcast (copy) a `double` from a memory location to all 4 elements of the result vector - `_mm256_ceil_pd`: round up each of 4 `double`s to the nearest integer - `_mm256_cmpeq_epi32`: compare 8+8 packed `int`s and return a mask that contains ones for equal element pairs - `_mm256_blendv_ps`: pick elements from one of two vectors according to a mask ---- Not a 1:1 mapping to assembly ```nasm vmovapd ymm1, YMMWORD PTR a[rax] ; t = a[i] vaddpd ymm0, ymm1, YMMWORD PTR b[rax] ; t += b[i] (fused!) vmovapd YMMWORD PTR c[rax], ymm0 ; c = a[i] ``` --- ## Vector Extensions ```cpp typedef int v8si __attribute__ (( vector_size(32) )); // type ^ ^ typename size in bytes ^ ``` Note this is a compiler-specific feature ---- ```cpp v4si a = {1, 2, 3, 5}; v4si b = {8, 13, 21, 34}; v4si c = a + b; for (int i = 0; i < 4; i++) printf("%d\n", c[i]); c *= 2; // multiply by scalar for (int i = 0; i < 4; i++) printf("%d\n", c[i]); ``` ---- ```cpp typedef double v4d __attribute__ (( vector_size(32) )); v4d a[100/4], b[100/4], c[100/4]; for (int i = 0; i < 100/4; i++) c[i] = a[i] + b[i]; ``` ---- ### Practical Tips - Compile to assembly: `g++ -S ...` (or go to godbolt.org) - See which loops get autovectorized: `g++ -fopt-info-vec-optimized ...` - Typedefs can be handy: `typedef __m256i reg` - You can use bitsets to "print" a SIMD register: ```cpp void print(__m256i v) { auto t = (unsigned*) &v; for (int i = 0; i < 8; i++) std::cout << std::bitset<32>(t[i]) << " "; std::cout << std::endl; } ``` --- ## Data Alignment The main disadvantage of SIMD is that you need to get data in vectors first (and sometimes preprocessing is not worth the trouble) ----  ----  ----  ---- For arrays, you have two options: 1. Pad them with neutal elements (e. g. zeros) 2. Break loop on last block and proceed normally Humans prefer #1, compilers prefer #2 <!-- .element: class="fragment" data-fragment-index="1" --> --- ## Reductions * Calculating A+B is easy, because there are no data dependencies * Calculating array sum is different: you need an accumulator from previous step * But we can calculate $B$ partial sums $\{i+kB\}$ for each $i<B$ and sum them up<!-- .element: class="fragment" data-fragment-index="1" --> This trick works with any other commutative operator (e. g. `min`) <!-- .element: class="fragment" data-fragment-index="1" --> ---- ```cpp int sum_simd(v8si *a, int n) { // ^ you can just cast a pointer normally, like with any other pointer type v8si s = {0}; for (int i = 0; i < n / 8; i++) s += a[i]; int res = 0; // sum 8 accumulators into one for (int i = 0; i < 8; i++) res += s[i]; // add the remainder of a for (int i = n / 8 * 8; i < n; i++) res += a[i]; return res; } ``` ---- ```cpp const int B = 2; int sum_simd_ilp(v8si *a, int n) { v8si b[B] = {0}; for (int i = 0; i < n / 8; i += B) for (int j = 0; j < B; j++) b[j] += a[i + j]; for (int i = 1; i < B; i++) b[0] += b[i]; int s = 0; for (int i = 0; i < 8; i++) s += b[0][i]; return s; } ``` 2x faster than `std::accumulate` (may be fixed in newer compilers) ----  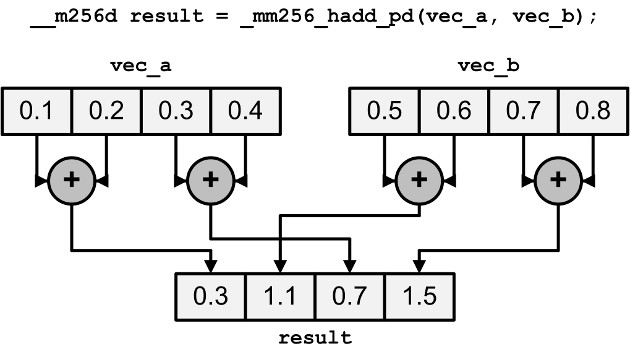Horizontal summation could be implemented a bit faster ---- ```cpp int hsum(__m256i x) { __m128i l = _mm256_extracti128_si256(x, 0); __m128i h = _mm256_extracti128_si256(x, 1); l = _mm_add_epi32(l, h); l = _mm_hadd_epi32(l, l); return _mm_extract_epi32(l, 0) + _mm_extract_epi32(l, 1); } ``` --- ## Memory Alignment There are two ways to read / write a SIMD block from memory: * `load` / `store` that segfault when the block doesn't fit a single cache line * `loadu` / `storeu` that always work but are slower ("u" stands for unaligned) When you can enforce aligned reads, always use the first one ---- Assuming that both arrays are initially aligned: ```cpp void aplusb_unaligned() { for (int i = 3; i + 7 < n; i += 8) { __m256i x = _mm256_loadu_si256((__m256i*) &a[i]); __m256i y = _mm256_loadu_si256((__m256i*) &b[i]); __m256i z = _mm256_add_epi32(x, y); _mm256_storeu_si256((__m256i*) &c[i], z); } } ``` ...will be 30% slower than this: ```cpp void aplusb_aligned() { for (int i = 0; i < n; i += 8) { __m256i x = _mm256_load_si256((__m256i*) &a[i]); __m256i y = _mm256_load_si256((__m256i*) &b[i]); __m256i z = _mm256_add_epi32(x, y); _mm256_store_si256((__m256i*) &c[i], z); } } ``` In unaligned version, half of reads will be the "bad" ones requesting two cache lines ---- So always ask the compiler to align memory for you: ```cpp alignas(32) float a[n]; for (int i = 0; i < n; i += 8) { __m256 x = _mm256_load_ps(&a[i]); // ... } ``` **GCC vector types require alignment** ---  --- ### Masking The main downside of SIMD is that there is no branching: we need to use predication ```cpp for (int i = 0; i < N; i++) a[i] = rand() % 100; int s = 0; // branch: for (int i = 0; i < N; i++) if (a[i] < 50) s += a[i]; // no branch: for (int i = 0; i < N; i++) s += (a[i] < 50) * a[i]; // also no branch: for (int i = 0; i < N; i++) s += (a[i] < 50 ? a[i] : 0); ``` ---- - `_mm256_cmpgt_epi32`: compare the integers in two vectors and produce a mask of all ones if the first element is more than the second and a zero otherwise - `_mm256_blendv_epi8`: blend (combine) the values of two vectors based on the provided mask ---- ```cpp const reg c = _mm256_set1_epi32(49); const reg z = _mm256_setzero_si256(); reg s = _mm256_setzero_si256(); for (int i = 0; i < N; i += 8) { reg x = _mm256_load_si256( (reg*) &a[i] ); reg mask = _mm256_cmpgt_epi32(x, c); x = _mm256_blendv_epi8(x, z, mask); s = _mm256_add_epi32(s, x); } ``` ---- In this particular case, we can use bitwise AND ```cpp const reg c = _mm256_set1_epi32(50); reg s = _mm256_setzero_si256(); for (int i = 0; i < N; i += 8) { reg x = _mm256_load_si256( (reg*) &a[i] ); reg mask = _mm256_cmpgt_epi32(c, x); x = _mm256_and_si256(x, mask); s = _mm256_add_epi32(s, x); } ``` Slightly faster because on this particular CPU, the vector `and` takes one cycle less than `blend` ---- - `_mm256_blend_epi32`: a `blend` that takes an 8-bit integer mask instead of a vector - `_mm256_maskload_epi32` and `_mm256_maskstore_epi32`: load/store a SIMD block from memory and `and` it with a mask in one go ---- We can also use predication with built-in vector types: ```cpp vec *v = (vec*) a; vec s = {}; for (int i = 0; i < N / 8; i++) s += (v[i] < 50 ? v[i] : 0); ``` All these versions work at around 13 GFLOP (and can also be auto-vectorized) (ILP?) --- ### Searching *Random* elements and queries ```cpp const int N = (1<<12); int a[N]; int find(int x) { for (int i = 0; i < N; i++) if (a[i] == x) return i; return -1; } ``` Measures ~4Gflops of virtual performance (including the elements that we haven't read) ---- Vectorized approach: - Compare a vector of `a` with the searched value for equality, producing a mask - Check if this mask is zero If it isn't, the needed element is somewhere within this block of 8, and we can find it scalarly ---- `_mm256_movemask_ps`: take the first bit of each 32-bit element in a vector and produce an 8-bit integer mask out of them We can check if this mask is non-zero — and if it is, also immediately get the index with the `ctz` instruction ---- ```cpp int find(int needle) { reg x = _mm256_set1_epi32(needle); for (int i = 0; i < N; i += 8) { reg y = _mm256_load_si256( (reg*) &a[i] ); reg m = _mm256_cmpeq_epi32(x, y); int mask = _mm256_movemask_ps((__m256) m); if (mask != 0) return i + __builtin_ctz(mask); } return -1; } ``` ~20 GFLOPS or about 5 times faster than the scalar one ---- ```nasm vpcmpeqd ymm0, ymm1, YMMWORD PTR a[0+rdx*4] vmovmskps eax, ymm0 test eax, eax je loop ``` ---- `_mm256_testz_si256` checks if a vector is zero (similar to the scalar `test`) ---- ```cpp int find(int needle) { reg x = _mm256_set1_epi32(needle); for (int i = 0; i < N; i += 8) { reg y = _mm256_load_si256( (reg*) &a[i] ); reg m = _mm256_cmpeq_epi32(x, y); if (!_mm256_testz_si256(m, m)) { int mask = _mm256_movemask_ps((__m256) m); return i + __builtin_ctz(mask); } } return -1; } ``` ---- We are still using `movemask` to do `ctz` later, but the hot loop is now one instruction shorter: ```nasm vpcmpeqd ymm0, ymm1, YMMWORD PTR a[0+rdx*4] vptest ymm0, ymm0 je loop ``` This doesn't improve performance much because `vptest` and `vmovmskps` have a the same throughput and bottleneck the performance ---- We can iterate in blocks of 16 elements and combine the results of independent comparisons of two vectors with a bitwise `or`: ```cpp int find(int needle) { reg x = _mm256_set1_epi32(needle); for (int i = 0; i < N; i += 16) { reg y1 = _mm256_load_si256( (reg*) &a[i] ); reg y2 = _mm256_load_si256( (reg*) &a[i + 8] ); reg m1 = _mm256_cmpeq_epi32(x, y1); reg m2 = _mm256_cmpeq_epi32(x, y2); reg m = _mm256_or_si256(m1, m2); if (!_mm256_testz_si256(m, m)) { int mask = (_mm256_movemask_ps((__m256) m2) << 8) + _mm256_movemask_ps((__m256) m1); return i + __builtin_ctz(mask); } } return -1; } ``` 20 → 34 GFLOPS Why not ~40? Shouldn't it be twice as fast? <!-- .element: class="fragment" data-fragment-index="1" --> ---- ```nasm vpcmpeqd ymm2, ymm1, YMMWORD PTR a[0+rdx*4] vpcmpeqd ymm3, ymm1, YMMWORD PTR a[32+rdx*4] vpor ymm0, ymm3, ymm2 vptest ymm0, ymm0 je loop ``` Every iteration, we need to execute 5 instructions, while the *decode width* of this CPU is 4, limiting the performance to ⅘ ---- To mitigate this, we can once again double the number of SIMD blocks we process on each iteration: ```cpp unsigned get_mask(reg m) { return _mm256_movemask_ps((__m256) m); } reg cmp(reg x, int *p) { reg y = _mm256_load_si256( (reg*) p ); return _mm256_cmpeq_epi32(x, y); } int find(int needle) { reg x = _mm256_set1_epi32(needle); for (int i = 0; i < N; i += 32) { reg m1 = cmp(x, &a[i]); reg m2 = cmp(x, &a[i + 8]); reg m3 = cmp(x, &a[i + 16]); reg m4 = cmp(x, &a[i + 24]); reg m12 = _mm256_or_si256(m1, m2); reg m34 = _mm256_or_si256(m3, m4); reg m = _mm256_or_si256(m12, m34); if (!_mm256_testz_si256(m, m)) { unsigned mask = (get_mask(m4) << 24) + (get_mask(m3) << 16) + (get_mask(m2) << 8) + get_mask(m1); return i + __builtin_ctz(mask); } } return -1; } ``` ~43 GFLOPS (~10x faster than the original scalar implementation) --- ### Counting Values ```cpp int count(int x) { int cnt = 0; for (int i = 0; i < N; i++) cnt += (a[i] == x); return cnt; } ``` ---- To vectorize it, we just need to convert the comparison mask to either one or zero per element and calculate the sum: ```cpp const reg ones = _mm256_set1_epi32(1); int count(int needle) { reg x = _mm256_set1_epi32(needle); reg s = _mm256_setzero_si256(); for (int i = 0; i < N; i += 8) { reg y = _mm256_load_si256( (reg*) &a[i] ); reg m = _mm256_cmpeq_epi32(x, y); m = _mm256_and_si256(m, ones); s = _mm256_add_epi32(s, m); } return hsum(s); } ``` Both implementations yield ~15 GFLOPS: the compiler can vectorize the first one all by itself ---- The mask of all ones is `-1` when reinterpreted as an integer We can skip the and-the-lowest-bit part and use the mask itself, and then just negate the final result: ```cpp int count(int needle) { reg x = _mm256_set1_epi32(needle); reg s = _mm256_setzero_si256(); for (int i = 0; i < N; i += 8) { reg y = _mm256_load_si256( (reg*) &a[i] ); reg m = _mm256_cmpeq_epi32(x, y); s = _mm256_add_epi32(s, m); } return -hsum(s); } ``` This doesn't improve the performance on this particular architecture because the throughput is bottlenecked by updating `s`: there is a dependency on the previous iteration ---- ```cpp int count(int needle) { reg x = _mm256_set1_epi32(needle); reg s1 = _mm256_setzero_si256(); reg s2 = _mm256_setzero_si256(); for (int i = 0; i < N; i += 16) { reg y1 = _mm256_load_si256( (reg*) &a[i] ); reg y2 = _mm256_load_si256( (reg*) &a[i + 8] ); reg m1 = _mm256_cmpeq_epi32(x, y1); reg m2 = _mm256_cmpeq_epi32(x, y2); s1 = _mm256_add_epi32(s1, m1); s2 = _mm256_add_epi32(s2, m2); } s1 = _mm256_add_epi32(s1, s2); return -hsum(s1); } ``` ~22 GFLOPS, reaching the memory bandwidth --- ### Argmin - We know how to compute minimum - We know how to find a given element - How to find the index of the minimum? ```cpp int argmin(int *a, int n) { int k = 0; for (int i = 0; i < n; i++) if (a[i] < a[k]) k = i; return k; } ``` ~1.5 GFLOPS (Random input) ---- ### Vector of Indices ```cpp // indices on the current iteration reg cur = _mm256_setr_epi32(0, 1, 2, 3, 4, 5, 6, 7); // the current minimum for each slice reg min = _mm256_set1_epi32(INT_MAX); // its index (argmin) for each slice reg idx = _mm256_setzero_si256(); for (int i = 0; i < n; i += 8) { // load a new SIMD block reg x = _mm256_load_si256((reg*) &a[i]); // find the slices where the minimum is updated reg mask = _mm256_cmpgt_epi32(min, x); // update the indices idx = _mm256_blendv_epi8(idx, cur, mask); // update the minimum (can also similarly use a "blend" here, but min is faster) min = _mm256_min_epi32(x, min); // update the current indices const reg eight = _mm256_set1_epi32(8); cur = _mm256_add_epi32(cur, eight); // // can also use a "blend" here, but min is faster } ``` 8-8.5 GFLOPS, with potential for ILP ---- When we run the scalar version, how often do we update the minimum? $$ \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \ldots + \frac{1}{n} = O(\ln(n)) $$ <!-- .element: class="fragment" data-fragment-index="1" --> The minimum is updated around 5 times for a hundred-element array, 7 for a thousand-element, and just 14 for a million-element array <!-- .element: class="fragment" data-fragment-index="1" --> ---- The compiler probably couldn't figure it out on its own, so let's explicitly provide this information: ```cpp int argmin(int *a, int n) { int k = 0; for (int i = 0; i < n; i++) if (a[i] < a[k]) [[unlikely]] k = i; return k; } ``` 1.5 → 2 GFLOPS ---- If we are only updating the minimum a dozen or so times during the entire computation, we can ditch vector-blending and index updating and maintain the minimum and regularly check if it has changed ---- A vector load, a comparison, and a test-if-zero: ```cpp int argmin(int *a, int n) { int min = INT_MAX, idx = 0; reg p = _mm256_set1_epi32(min); for (int i = 0; i < n; i += 8) { reg y = _mm256_load_si256((reg*) &a[i]); reg mask = _mm256_cmpgt_epi32(p, y); if (!_mm256_testz_si256(mask, mask)) { [[unlikely]] for (int j = i; j < i + 8; j++) if (a[j] < min) min = a[idx = j]; p = _mm256_set1_epi32(min); } } return idx; } ``` ~8.5 GFLOPS `testz` is the bottleneck with a throughput of one, but we know how to solve this <!-- .element: class="fragment" data-fragment-index="1" --> ---- ```cpp int argmin(int *a, int n) { int min = INT_MAX, idx = 0; reg p = _mm256_set1_epi32(min); for (int i = 0; i < n; i += 16) { reg y1 = _mm256_load_si256((reg*) &a[i]); reg y2 = _mm256_load_si256((reg*) &a[i + 8]); reg y = _mm256_min_epi32(y1, y2); reg mask = _mm256_cmpgt_epi32(p, y); if (!_mm256_testz_si256(mask, mask)) { [[unlikely]] for (int j = i; j < i + 16; j++) if (a[j] < min) min = a[idx = j]; p = _mm256_set1_epi32(min); } } return idx; } ``` ~10 GFLOPS ---- - Increase the block size to 32 elements to allow more ILP - Optimize the local argmin: save the index of the block and come back at the end ---- ```cpp int argmin(int *a, int n) { int min = INT_MAX, idx = 0; reg p = _mm256_set1_epi32(min); for (int i = 0; i < n; i += 32) { reg y1 = _mm256_load_si256((reg*) &a[i]); reg y2 = _mm256_load_si256((reg*) &a[i + 8]); reg y3 = _mm256_load_si256((reg*) &a[i + 16]); reg y4 = _mm256_load_si256((reg*) &a[i + 24]); y1 = _mm256_min_epi32(y1, y2); y3 = _mm256_min_epi32(y3, y4); y1 = _mm256_min_epi32(y1, y3); reg mask = _mm256_cmpgt_epi32(p, y1); if (!_mm256_testz_si256(mask, mask)) { [[unlikely]] idx = i; for (int j = i; j < i + 32; j++) min = (a[j] < min ? a[j] : min); p = _mm256_set1_epi32(min); } } for (int i = idx; i < idx + 31; i++) if (a[i] == min) return i; return idx + 31; } ``` ~22 GFLOPS ---- What if the array is decreasing? ---- Find the Minimum, Then Find the Index: ```cpp int argmin(int *a, int n) { int needle = min(a, n); int idx = find(a, n, needle); return idx; } ``` ~18 / ~12 GFLOPS for random / decreasing arrays ---- - Split the array into blocks of fixed size $B$ - Compute the minima on these blocks while also maintaining the global minimum - Come back to minimum block and find exact argmin - We process $(N + B)$ elements and sacrifice not ½ nor ⅓ of the performance ---- ```cpp const int B = 256; // returns the minimum and its first block pair<int, int> approx_argmin(int *a, int n) { int res = INT_MAX, idx = 0; for (int i = 0; i < n; i += B) { int val = min(a + i, B); if (val < res) { res = val; idx = i; } } return {res, idx}; } int argmin(int *a, int n) { auto [needle, base] = approx_argmin(a, n); int idx = find(a + base, B, needle); return base + idx; } ``` ~22 / ~19 GFLOPS ---- ``` algorithm rand decr reason for the performance difference ----------- ----- ----- ------------------------------------------------------------- std 0.28 0.28 scalar 1.54 1.89 efficient branch prediction + hinted 1.95 0.75 wrong hint index 8.17 8.12 simd 8.51 1.65 scalar-based argmin on each iteration + ilp 10.22 1.74 ^ same + optimized 22.44 2.70 ^ same, but faster because there are less inter-dependencies min+find 18.21 12.92 find() has to scan the entire array + blocked 22.23 19.29 we still have an optional horizontal minimum every B elements ``` --- ### Shuffles and Popcount `popcnt` was added around 2008 with SSE4: ```cpp const int N = (1<<12); int a[N]; int popcnt() { int res = 0; for (int i = 0; i < N; i++) res += __builtin_popcount(a[i]); return res; } ``` It also supports 64-bit integers, improving the total throughput twofold: ```cpp int popcnt_ll() { long long *b = (long long*) a; int res = 0; for (int i = 0; i < N / 2; i++) res += __builtin_popcountl(b[i]); return res; } ``` Load-fused popcount and addition $8+8=16$ bytes per cycle, limited by the decode width of 4 ---- Let's pretend that we are back in the mid-2000s ```cpp __attribute__ (( optimize("no-tree-vectorize") )) int popcnt() { int res = 0; for (int i = 0; i < N; i++) for (int l = 0; l < 32; l++) res += (a[i] >> l & 1); return res; } ``` ~0.2: just slightly faster than ⅛-th of a byte per cycle ---- Precompute a small 256-element *lookup table* with popcounts of individual bytes ```cpp struct Precalc { alignas(64) char counts[256]; constexpr Precalc() : counts{} { for (int m = 0; m < 256; m++) for (int i = 0; i < 8; i++) counts[m] += (m >> i & 1); } }; constexpr Precalc P; int popcnt() { auto b = (unsigned char*) a; // careful: plain "char" is signed int res = 0; for (int i = 0; i < 4 * N; i++) res += P.counts[b[i]]; return res; } ``` ~2 bytes per cycle (~2.7 if we switch to `unsigned short`) ---- - We can make the lookup table small enough to fit inside a register and use [pshufb](https://software.intel.com/sites/landingpage/IntrinsicsGuide/#text=pshuf&techs=AVX,AVX2&expand=6331) to look up its values in parallel - The original 128-bit `pshufb` takes two registers: the lookup table containing 16 byte values and a vector of 16 4-bit indices (0 to 15), specifying which bytes to pick for each position - In 256-bit AVX2, instead of a 32-byte lookup table with awkward 5-bit indices, the instruction applies the shuffling operation independently over 128-bit lanes The `pshufb` instruction is so instrumental in some SIMD algorithms that [Wojciech Muła](http://0x80.pl/) (author of this algorithm) took it as his [Twitter handle](https://twitter.com/pshufb) ---- We create a 16-byte lookup table with population counts for each nibble (half-byte), repeated twice: ```cpp const reg lookup = _mm256_setr_epi8( /* 0 */ 0, /* 1 */ 1, /* 2 */ 1, /* 3 */ 2, /* 4 */ 1, /* 5 */ 2, /* 6 */ 2, /* 7 */ 3, /* 8 */ 1, /* 9 */ 2, /* a */ 2, /* b */ 3, /* c */ 2, /* d */ 3, /* e */ 3, /* f */ 4, /* 0 */ 0, /* 1 */ 1, /* 2 */ 1, /* 3 */ 2, /* 4 */ 1, /* 5 */ 2, /* 6 */ 2, /* 7 */ 3, /* 8 */ 1, /* 9 */ 2, /* a */ 2, /* b */ 3, /* c */ 2, /* d */ 3, /* e */ 3, /* f */ 4 ); ``` To compute the population count of a vector, we split each of its bytes into the lower and higher nibbles and then use this lookup table to retrieve their counts ---- ```cpp const reg low_mask = _mm256_set1_epi8(0x0f); int popcnt() { int k = 0; reg t = _mm256_setzero_si256(); for (; k + 15 < N; k += 15) { reg s = _mm256_setzero_si256(); for (int i = 0; i < 15; i += 8) { reg x = _mm256_load_si256( (reg*) &a[k + i] ); reg l = _mm256_and_si256(x, low_mask); reg h = _mm256_and_si256(_mm256_srli_epi16(x, 4), low_mask); reg pl = _mm256_shuffle_epi8(lookup, l); reg ph = _mm256_shuffle_epi8(lookup, h); s = _mm256_add_epi8(s, pl); s = _mm256_add_epi8(s, ph); } t = _mm256_add_epi64(t, _mm256_sad_epu8(s, _mm256_setzero_si256())); } int res = hsum(t); while (k < N) res += __builtin_popcount(a[k++]); return res; } ``` ~30 bytes per cycle (theoretically, the inner loop could do 32, but we have to stop it every 15 iterations because the 8-bit counters can overflow) We can calculate population counts even faster: https://arxiv.org/pdf/1611.07612 <!-- .element: class="fragment" data-fragment-index="1" --> --- ## Filtering ```cpp int a[N], b[N]; int filter() { int k = 0; for (int i = 0; i < N; i++) if (a[i] < P) b[k++] = a[i]; return k; } ``` 0.7-1.5 GFLOPS depending on `P` (similar to the branching case study) ---- `_mm256_permutevar8x32_epi32` takes a vector of values and individually selects them with a vector of indices Despite the name, it doesn't *permute* values but just *copies* them to form a new vector (duplicates in the result are allowed) ---- - calculate the predicate on a vector of data - use the `movemask` instruction to get a scalar 8-bit mask - use this mask to index a lookup table, returning a permutation moving the required elements to the beginning of the vector (in their original order) - use the `_mm256_permutevar8x32_epi32` intrinsic to permute the values - write the whole permuted vector to the buffer - popcount the mask and move the buffer pointer by that amount ---- First, we need to precompute the permutations: ```cpp struct Precalc { alignas(64) int permutation[256][8]; constexpr Precalc() : permutation{} { for (int m = 0; m < 256; m++) { int k = 0; for (int i = 0; i < 8; i++) if (m >> i & 1) permutation[m][k++] = i; } } }; constexpr Precalc T; ``` ---- ```cpp const reg p = _mm256_set1_epi32(P); int filter() { int k = 0; for (int i = 0; i < N; i += 8) { reg x = _mm256_load_si256( (reg*) &a[i] ); reg m = _mm256_cmpgt_epi32(p, x); int mask = _mm256_movemask_ps((__m256) m); reg permutation = _mm256_load_si256( (reg*) &T.permutation[mask] ); x = _mm256_permutevar8x32_epi32(x, permutation); _mm256_storeu_si256((reg*) &b[k], x); k += __builtin_popcount(mask); } return k; } ``` ----  6-7x faster than the scalar one Much faster on AVX512: it has a dedicated `compress` instruction <!-- .element: class="fragment" data-fragment-index="1" --> --- ## Prefix Sum Prefix sum is a very important parallel computing primitive ```cpp void prefix(int *a, int n) { for (int i = 1; i < n; i++) a[i] += a[i - 1]; } ``` 1.2-1.6 GFLOPS depending on the array size ---- Seems like two reads, an add, and a write on each iteration, but the compiler optimizes the extra read away: ```nasm loop: add edx, DWORD PTR [rax] mov DWORD PTR [rax-4], edx add rax, 4 cmp rax, rcx jne loop ``` Only fused read-add and the write-back of the result remain after unrolling (theoretically 2 GFLOPS but we have memory issues) ----  - split the array into blocks - independently calculate local prefix sums - do a second pass where we adjust the computed values in each block Usually split in as many blocks as you have processors, but we can't do that in SIMD Instead, we will split in SIMD lanes calculate prefix sums within a register <!-- .element: class="fragment" data-fragment-index="1" --> ---- To compute prefix sums locally, we perform $\log n$ iterations where on $k$-th iteration, we add $a_{i - 2^k}$ to $a_i$ for all applicable $i$: ```cpp for (int l = 0; l < logn; l++) // (atomically and in parallel): for (int i = (1 << l); i < n; i++) a[i] += a[i - (1 << l)]; ``` The total work is $O(n \log n)$ instead of linear, but we can't avoid it ---- Permutations are slow; `sll` ("shift lanes left") does what we need: ```cpp typedef __m128i v4i; v4i prefix(v4i x) { // x = 1, 2, 3, 4 x = _mm_add_epi32(x, _mm_slli_si128(x, 4)); // x = 1, 2, 3, 4 // + 0, 1, 2, 3 // = 1, 3, 5, 7 x = _mm_add_epi32(x, _mm_slli_si128(x, 8)); // x = 1, 3, 5, 7 // + 0, 0, 1, 3 // = 1, 3, 6, 10 return s; } ``` ---- The 256-bit version of performs byte shift independently within two 128-bit lanes: ```cpp typedef __m256i v8i; v8i prefix(v8i x) { // x = 1, 2, 3, 4, 5, 6, 7, 8 x = _mm256_add_epi32(x, _mm256_slli_si256(x, 4)); x = _mm256_add_epi32(x, _mm256_slli_si256(x, 8)); x = _mm256_add_epi32(x, _mm256_slli_si256(x, 16)); // <- this does nothing // x = 1, 3, 6, 10, 5, 11, 18, 26 return s; } ``` (This is typical for AVX2) ---- ```cpp void prefix(int *p) { v8i x = _mm256_load_si256((v8i*) p); x = _mm256_add_epi32(x, _mm256_slli_si256(x, 4)); x = _mm256_add_epi32(x, _mm256_slli_si256(x, 8)); _mm256_store_si256((v8i*) p, x); } ``` ---- ```cpp v4i accumulate(int *p, v4i s) { v4i d = (v4i) _mm_broadcast_ss((float*) &p[3]); v4i x = _mm_load_si128((v4i*) p); x = _mm_add_epi32(s, x); _mm_store_si128((v4i*) p, x); return _mm_add_epi32(s, d); } ``` ---- ```cpp void prefix(int *a, int n) { for (int i = 0; i < n; i += 8) prefix(&a[i]); v4i s = _mm_setzero_si128(); for (int i = 4; i < n; i += 4) s = accumulate(&a[i], s); } ``` ----  Memory bandwidth issues ---- ```cpp const int B = 64; void prefix(int *a, int n) { v4i s = _mm_setzero_si128(); for (int i = 0; i < B; i += 8) prefix(&a[i]); for (int i = B; i < n; i += 8) { __builtin_prefetch(&a[i + (1<<10)]); prefix(&a[i]); s = accumulate(&a[i - B], s); s = accumulate(&a[i - B + 4], s); } for (int i = n - B; i < n; i += 4) s = accumulate(&a[i], s); } ``` ----  --- Next week: memory