<style> .reveal { font-size: 24px; } .reveal section img { background:none; border:none; box-shadow:none; } pre.graphviz { box-shadow: none; } </style> # Data Parallelism High Performance Computing, Lecture 3 Sergey Slotin Dec 27, 2020 --- ## Recall: Superscalar Processors * Any instruction execution takes multiple steps * To hide latency, everything is pipelined * You can get CPI < 1 if you have more than one of each execution unit * Performance engineering is basically about avoiding pipeline stalls  --- ## Single Instruction, Multple Data  Instructions that perform the same operation on multiple data points (blocks of 128, 256 or 512 bits, also called *vectors*) ----  Backwards-compatible up until AVX-512 (x86 specific; ARM and others have similar instruction sets) ---- You can check compatibility during runtime: ```cpp cout << __builtin_cpu_supports("sse") << endl; cout << __builtin_cpu_supports("sse2") << endl; cout << __builtin_cpu_supports("avx") << endl; cout << __builtin_cpu_supports("avx2") << endl; cout << __builtin_cpu_supports("avx512f") << endl; ``` ...or call `cat /proc/cpuinfo` and see CPU flags along with other info --- ## How to Use SIMD Converting a program from scalar to vector one is called *vectorization*, which can be achieved using a combination of: * x86 assembly * **C/C++ intrinsics** * Vector types * SIMD libraries * **Auto-vectorization** Later are simpler, former are more flexible ---- ### Intel Intrinsics Guide  Because nobody likes to write assembly https://software.intel.com/sites/landingpage/IntrinsicsGuide/ ---- All C++ intrinsics can be included with `x86intrin.h` ```cpp #pragma GCC target("avx2") #pragma GCC optimize("O3") #include <x86intrin.h> #include <bits/stdc++.h> using namespace std; ``` You can also drop pragmas and compile with `-O3 -march=native` instead --- ## The A+B Problem ```cpp const int n = 1e5; int a[n], b[n], c[n]; for (int t = 0; t < 100000; t++) for (int i = 0; i < n; i++) c[i] = a[i] + b[i]; ``` Twice as fast (!) if you compile with AVX instruction set (i. e. add `#pragma GCC target("avx2")` or `-march=native`) ---- ## What Actually Happens ```cpp double a[100], b[100], c[100]; for (int i = 0; i < 100; i += 4) { // load two 256-bit arrays into their respective registers __m256d x = _mm256_loadu_pd(&a[i]); __m256d y = _mm256_loadu_pd(&b[i]); // - 256 is the block size // - d stands for "double" // - pd stands for "packed double" // perform addition __m256d z = _mm256_add_pd(x, y); // write the result back into memory _mm256_storeu_pd(&c[i], z); } ``` (I didn't come up with the op naming, don't blame me) ---- ### More examples * `_mm_add_epi16`: adds two 16-bit extended packed integers (128/16=8 short ints) * `_mm256_acos_pd`: computes acos of 256/64=4 doubles * `_mm256_broadcast_sd`: creates 4 copies of a number in a "normal" register * `_mm256_ceil_pd`: rounds double up to nearest int * `_mm256_cmpeq_epi32`: compares 8+8 packed ints and returns a (vector) mask that contains ones for elements that are equal * `_mm256_blendv_ps`: blends elements from either one vector or another according to a mask (vectorized cmov, could be used to replace `if`) ---- ### Vector Types For some reason, C++ intrinsics have explicit typing, for example on AVX: * `__m256` means float and only instructions ending with "ps" work * `__m256d` means double and only instructions ending with "pd" work * `__m256i` means different integers and only instructions ending with "epi/epu" wor You can freely convert between them with C-style casting ---- Also, compiles have their own vector types: ```cpp typedef float float8_t __attribute__ (( vector_size (8 * sizeof(float)) )); float8_t v; float first_element = v[0]; // you can index them as arrays float8_t v_squared = v * v; // you can use a subset of normal C operations float8_t v_doubled = _mm256_movemask_ps(v); // all C++ instrinsics work too ``` Note that this is a GCC feature; it will probably be standartized in C++ someday https://gcc.gnu.org/onlinedocs/gcc-4.7.2/gcc/Vector-Extensions.html --- ## Data Alignment The main disadvantage of SIMD is that you need to get data in vectors first (and sometimes preprocessing is not worth the trouble) <!-- .element: class="fragment" data-fragment-index="1" --> ----  ----  ----  ---- For arrays, you have two options: 1. Pad them with neutal elements (e. g. zeros) 2. Break loop on last block and proceed normally Humans prefer #1, compilers prefer #2 <!-- .element: class="fragment" data-fragment-index="1" --> --- ## Reductions * Calculating A+B is easy, because there are no data dependencies * Calculating array sum is different: you need an accumulator from previous step * But we can calculate $B$ partial sums $\{i+kB\}$ for each $i<B$ and sum them up<!-- .element: class="fragment" data-fragment-index="1" -->  <!-- .element: class="fragment" data-fragment-index="1" --> This trick works with any other commutative operator <!-- .element: class="fragment" data-fragment-index="1" --> ---- Explicitly using C++ intrinsics: ```cpp int sum(int a[], int n) { int res = 0; // we will store 8 partial sums here __m256i x = _mm256_setzero_si256(); for (int i = 0; i + 8 < n; i += 8) { __m256i y = _mm256_loadu_si256((__m256i*) &a[i]); // add all 8 new numbers at once to their partial sums x = _mm256_add_epi32(x, y); } // sum 8 elements in our vector ("horizontal sum") int *b = (int*) &x; for (int i = 0; i < 8; i++) res += b[i]; // add what's left of the array in case n % 8 != 0 for (int i = (n / 8) * 8; i < n; i++) res += a[i]; return res; } ``` (Don't implement it yourself, compilers are smart enough to vectorize) ----  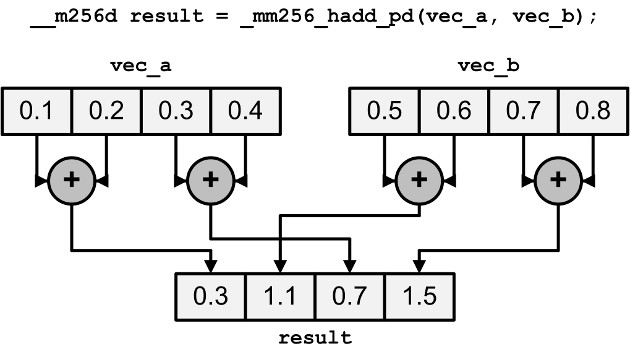Horizontal addition could be implemented a bit faster --- ## Memory Alignment There are two ways to read / write a SIMD block from memory: * `load` / `store` that segfault when the block doesn't fit a single cache line * `loadu` / `storeu` that always work but are slower ("u" stands for unaligned) When you can enforce aligned reads, always use the first one ---- Assuming that both arrays are initially aligned: ```cpp void aplusb_unaligned() { for (int i = 3; i + 7 < n; i += 8) { __m256i x = _mm256_loadu_si256((__m256i*) &a[i]); __m256i y = _mm256_loadu_si256((__m256i*) &b[i]); __m256i z = _mm256_add_epi32(x, y); _mm256_storeu_si256((__m256i*) &c[i], z); } } ``` ...will be 30% slower than this: ```cpp void aplusb_aligned() { for (int i = 0; i < n; i += 8) { __m256i x = _mm256_load_si256((__m256i*) &a[i]); __m256i y = _mm256_load_si256((__m256i*) &b[i]); __m256i z = _mm256_add_epi32(x, y); _mm256_store_si256((__m256i*) &c[i], z); } } ``` In unaligned version, half of reads will be the "bad" ones requesting two cache lines ---- So always ask compiler to align memory for you: ```cpp alignas(32) float a[n]; for (int i = 0; i < n; i += 8) { __m256 x = _mm256_load_ps(&a[i]); // ... } ``` (This is also why compilers can't always auto-vectorize efficiently) <!-- .element: class="fragment" data-fragment-index="1" --> --- ## Loop Unrolling Simple loops often have some overhead from iterating: ```cpp for (int i = 1; i < n; i++) a[i] = (i % b[i]); ``` It is often benefitial to "unroll" them like this: ```cpp int i; for (i = 1; i < n - 3; i += 4) { a[i] = (i % b[i]); a[i + 1] = ((i + 1) % b[i + 1]); a[i + 2] = ((i + 2) % b[i + 2]); a[i + 3] = ((i + 3) % b[i + 3]); } for (; i < n; i++) a[i] = (i % b[i]); ``` There are trade-offs to it, and compilers are sometimes wrong Use `#pragma unroll` and `-unroll-loops` to hint compiler what to do --- ## More on Pipelining  https://uops.info ---- For example, in Sandy Bridge family there are 6 execution ports: * Ports 0, 1, 5 are for arithmetic and logic operations (ALU) * Ports 2, 3 are for memory reads * Port 4 is for memory write You can lookup them up in instruction tables and see figure out which one is the bottleneck --- ## SIMD + ILP * As all instructions, SIMD operations can be pipelined too * To leverage it, we need to create opportunities for instruction-level parallelism * A+B is fine, but array sum still has dependency on the previous vector <!-- .element: class="fragment" data-fragment-index="1" --> * Apply the same trick: calculate partial sums, but using multiple registers <!-- .element: class="fragment" data-fragment-index="2" --> ---- For example, instead of this: ```cpp s += a0; s += a1; s += a2; s += a3; ... ``` ...we split it between accumulators and utilize ILP: ```cpp s0 += a0; s1 += a1; s0 += a2; s1 += a3; ... s = s0 + s1; ``` --- ## Practical Tips * Compile to assembly: `g++ -S ...` (or go to godbolt.org) * See which loops get autovectorized: `g++ -fopt-info-vec-optimized ...` * Typedefs can be handy: `typedef __m256i reg` * You can use bitsets to "print" a SIMD register: ```cpp template<typename T> void print(T var) { unsigned *val = (unsigned*) &var; for (int i = 0; i < 4; i++) cout << bitset<32>(val[i]) << " "; cout << endl; } ``` --- # Demo Time --- ## Case Study: Distance Product (We are going to speedrun "[Programming Parallel Computers](http://ppc.cs.aalto.fi/ch2/)" course) Given a matrix $D$, we need to calculate its "min-plus matrix multiplication" defined as: $(D \circ D)_{ij} = \min_k(D_{ik} + D_{kj})$ ---- Graph interpretation: find shortest paths of length 2 between all vertices in a fully-connected weighted graph  ---- A cool thing about distance product is that if if we iterate the process and calculate: $D_2 = D \circ D, \;\; D_4 = D_2 \circ D_2, \;\; D_8 = D_4 \circ D_4, \;\; \ldots$ Then we can find all-pairs shortest distances in $O(\log n)$ steps (but recall that there are [more direct ways](https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm) to solve it) <!-- .element: class="fragment" data-fragment-index="1" --> --- ## V0: Baseline Implement the definition of what we need to do, but using arrays instead of matrices: ```cpp const float infty = std::numeric_limits<float>::infinity(); void step(float* r, const float* d, int n) { for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { float v = infty; for (int k = 0; k < n; ++k) { float x = d[n*i + k]; float y = d[n*k + j]; float z = x + y; v = std::min(v, z); } r[n*i + j] = v; } } } ``` Compile with `g++ -O3 -march=native -std=c++17` On our Intel Core i5-6500 ("Skylake", 4 cores, 3.6 GHz) with $n=4000$ it runs for 99s, which amounts to ~1.3B useful floating point operations per second --- ## Theoretical Performance $$ \underbrace{4}_{CPUs} \cdot \underbrace{8}_{SIMD} \cdot \underbrace{2}_{1/thr} \cdot \underbrace{3.6 \cdot 10^9}_{cycles/sec} = 230.4 \; GFLOPS \;\; (2.3 \cdot 10^{11}) $$ RAM bandwidth: 34.1 GB/s (or ~10 bytes per cycle) <!-- .element: class="fragment" data-fragment-index="1" --> --- ## OpenMP * We have 4 cores, so why don't we use them? * There are low-level ways of creating threads, but they involve a lot of code * We will use a high-level interface called OpenMP * (We will talk about multithreading in much more detail on the next lecture)  ---- ## Multithreading Made Easy All you need to know for now is the `#pragma omp parallel for` directive ```cpp #pragma omp parallel for for (int i = 0; i < 10; ++i) { do_stuff(i); } ``` It splits iterations of a loop among multiple threads There are many ways to control scheduling, but we'll just leave defaults because our use case is simple <!-- .element: class="fragment" data-fragment-index="1" --> ---- ## Warning: Data Races This only works when all iterations can safely be executed simultaneously It's not always easy to determine, but for now following rules of thumb are enough: * There must not be any shared data element that is read by X and written by Y * There must not be any shared data element that is written by X and written by Y E. g. sum can't be parallelized this way, as threads would modify a shared variable <!-- .element: class="fragment" data-fragment-index="1" --> --- ## Parallel Baseline OpenMP is included in compilers: just add `-fopenmp` flag and that's it ```cpp void step(float* r, const float* d, int n) { #pragma omp parallel for for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { float v = infty; for (int k = 0; k < n; ++k) { float x = d[n*i + k]; float y = d[n*k + j]; float z = x + y; v = std::min(v, z); } r[n*i + j] = v; } } } ``` Runs ~4x times faster, as it should --- ## Memory Bottleneck  (It is slower on macOS because of smaller page sizes) ---- ## Virtual Memory  --- ## V1: Linear Reading Just transpose it, as we did with matrices ```cpp void step(float* r, const float* d, int n) { std::vector<float> t(n*n); #pragma omp parallel for for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { t[n*j + i] = d[n*i + j]; } } #pragma omp parallel for for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { float v = std::numeric_limits<float>::infinity(); for (int k = 0; k < n; ++k) { float x = d[n*i + k]; float y = t[n*j + k]; float z = x + y; v = std::min(v, z); } r[n*i + j] = v; } } } ``` ----  ----  --- ## V2: Instruction-Level Parallelism We can apply the same trick as we did with array sum earlier, so that instead of: ```cpp v = min(v, z0); v = min(v, z1); v = min(v, z2); v = min(v, z3); v = min(v, z4); ``` We use a few registers and compute minimum simultaneously utilizing ILP: ```cpp v0 = min(v0, z0); v1 = min(v1, z1); v0 = min(v0, z2); v1 = min(v1, z3); v0 = min(v0, z4); ... v = min(v0, v1); ``` ----  Our memory layout looks like this now ---- ```cpp void step(float* r, const float* d_, int n) { constexpr int nb = 4; int na = (n + nb - 1) / nb; int nab = na*nb; // input data, padded std::vector<float> d(n*nab, infty); // input data, transposed, padded std::vector<float> t(n*nab, infty); #pragma omp parallel for for (int j = 0; j < n; ++j) { for (int i = 0; i < n; ++i) { d[nab*j + i] = d_[n*j + i]; t[nab*j + i] = d_[n*i + j]; } } #pragma omp parallel for for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { // vv[0] = result for k = 0, 4, 8, ... // vv[1] = result for k = 1, 5, 9, ... // vv[2] = result for k = 2, 6, 10, ... // vv[3] = result for k = 3, 7, 11, ... float vv[nb]; for (int kb = 0; kb < nb; ++kb) { vv[kb] = infty; } for (int ka = 0; ka < na; ++ka) { for (int kb = 0; kb < nb; ++kb) { float x = d[nab*i + ka * nb + kb]; float y = t[nab*j + ka * nb + kb]; float z = x + y; vv[kb] = std::min(vv[kb], z); } } // v = result for k = 0, 1, 2, ... float v = infty; for (int kb = 0; kb < nb; ++kb) { v = std::min(vv[kb], v); } r[n*i + j] = v; } } } ``` ----  --- ## V3: Vectorization  ---- ```cpp static inline float8_t min8(float8_t x, float8_t y) { return x < y ? x : y; } void step(float* r, const float* d_, int n) { // elements per vector constexpr int nb = 8; // vectors per input row int na = (n + nb - 1) / nb; // input data, padded, converted to vectors float8_t* vd = float8_alloc(n*na); // input data, transposed, padded, converted to vectors float8_t* vt = float8_alloc(n*na); #pragma omp parallel for for (int j = 0; j < n; ++j) { for (int ka = 0; ka < na; ++ka) { for (int kb = 0; kb < nb; ++kb) { int i = ka * nb + kb; vd[na*j + ka][kb] = i < n ? d_[n*j + i] : infty; vt[na*j + ka][kb] = i < n ? d_[n*i + j] : infty; } } } #pragma omp parallel for for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { float8_t vv = f8infty; for (int ka = 0; ka < na; ++ka) { float8_t x = vd[na*i + ka]; float8_t y = vt[na*j + ka]; float8_t z = x + y; vv = min8(vv, z); } r[n*i + j] = hmin8(vv); } } std::free(vt); std::free(vd); } ``` ----  --- ## V4: Register Reuse * At this point we are actually bottlenecked by memory * It turns out that calculating one $r_{ij}$ at a time is not optimal * We can reuse data that we read into registers to update other fields ----  ---- ```cpp for (int ka = 0; ka < na; ++ka) { float8_t y0 = vt[na*(jc * nd + 0) + ka]; float8_t y1 = vt[na*(jc * nd + 1) + ka]; float8_t y2 = vt[na*(jc * nd + 2) + ka]; float8_t x0 = vd[na*(ic * nd + 0) + ka]; float8_t x1 = vd[na*(ic * nd + 1) + ka]; float8_t x2 = vd[na*(ic * nd + 2) + ka]; vv[0][0] = min8(vv[0][0], x0 + y0); vv[0][1] = min8(vv[0][1], x0 + y1); vv[0][2] = min8(vv[0][2], x0 + y2); vv[1][0] = min8(vv[1][0], x1 + y0); vv[1][1] = min8(vv[1][1], x1 + y1); vv[1][2] = min8(vv[1][2], x1 + y2); vv[2][0] = min8(vv[2][0], x2 + y0); vv[2][1] = min8(vv[2][1], x2 + y1); vv[2][2] = min8(vv[2][2], x2 + y2); } ``` Ugly, but worth it ----  --- ## V5: More Register Reuse  ----  --- ## V6: Software Prefetching  --- ## V7: Temporal Cache Locality  ---- ### Z-Curve  ----  --- ## Summary * Deal with memory problems first (make sure data fits L3 cache) * SIMD can get you ~10x speedup * ILP can get you 2-3x speedup * Multi-core parallelism can get you $NUM_CORES speedup (and it can be just one `#pragma omp parallel for` away) --- ## Next time * Into to concurrency and parallel algorithms * Threads, mutexes, channels and other syncronization * Will try to keep up with exercises on github Additional reading: * [Tutorial on x86 SIMD](http://www.lighterra.com/papers/modernmicroprocessors/) by me (in Russian) * [Programming Parallel Computers](http://ppc.cs.aalto.fi/ch2/) by Jukka Suomela * [Optimizing Software in C++](https://www.agner.org/optimize/) by Agner Fog (among his other manuals)