<style> .reveal { font-size: 24px; } .reveal section img { background:none; border:none; box-shadow:none; } pre.graphviz { box-shadow: none; } </style> # Optimizing Binary Search C++ Zero Cost Conf Sergey Slotin (13 Jul 2022, draft) --- ## About me - Wrote [Algorithms for Modern Hardware](https://en.algorithmica.org/hpc/) (en.algorithmica.org/hpc) - Designed the world's fastest **binary search**, B-tree, integer parsing, factorization, prefix sum, array searching, argmin… (github.com/sslotin/amh-code) - Email: me@sereja.me; Twitter: [@sergey_slotin](https://twitter.com/sergey_slotin); Telegram: [@bydlokoder](https://t.me/bydlokoder) <!-- ## Outline - ??? - ??? - 15x faster `std::lower_bound` --> --- ## Binary search ---- ```cpp // perform any O(n) precomputation with a sorted array void prepare(int *a, int n); // return the first element y ≥ x in O(log n) int lower_bound(int x); ``` Random array & queries, all 32-bit integers, optimize for **throughput** ----  ---- ```cpp int lower_bound(int x) { int l = 0, r = n - 1; while (l < r) { int m = (l + r) / 2; if (t[m] >= x) r = m; else l = m + 1; } return t[l]; } ``` ---- ```cpp template <class _Compare, class _ForwardIterator, class _Tp> _LIBCPP_CONSTEXPR_AFTER_CXX17 _ForwardIterator __lower_bound(_ForwardIterator __first, _ForwardIterator __last, const _Tp& __value_, _Compare __comp) { typedef typename iterator_traits<_ForwardIterator>::difference_type difference_type; difference_type __len = _VSTD::distance(__first, __last); while (__len != 0) { difference_type __l2 = _VSTD::__half_positive(__len); _ForwardIterator __m = __first; _VSTD::advance(__m, __l2); if (__comp(*__m, __value_)) { __first = ++__m; __len -= __l2 + 1; } else __len = __l2; } return __first; } ``` github.com/llvm-mirror/libcxx/blob/master/include/algorithm#L4169 ---- ```nasm │35: mov %rax,%rdx 0.52 │ sar %rdx 0.33 │ lea (%rsi,%rdx,4),%rcx 4.30 │ cmp (%rcx),%edi 65.39 │ ↓ jle b0 0.07 │ sub %rdx,%rax 9.32 │ lea 0x4(%rcx),%rsi 0.06 │ dec %rax 1.37 │ test %rax,%rax 1.11 │ ↑ jg 35 ``` perf record & perf report ($n=10^6$) <!-- (comment: maybe live demo?) --> ----  Zen 2 @ 2GHz, DDR4 @ 2667MHz ----  L1 access is ~2ns, RAM is ~100ns, HDD is ~10ms ----  $\frac{100}{13} \times 2 \approx 15$ cycles per iteration seems too high for L1 --- ## Pipelining ---- To execute *any* instruction, processors need to do a lot of preparatory work: - **fetch** a chunk of machine code from memory - **decode** it and split into instructions - **execute** these instructions (possibly involving some **memory** operations) - **write** the results back into registers This whole sequence of operations takes up to 15-20 CPU cycles ---- *Pipelining*: after an instruction passes through the first stage, the next one is processed the right away, without waiting for the previous one to fully complete  Does not reduce *actual* latency but makes it seem like if it was composed of only the execution and memory stage ----  Real-world analogy: Henry Ford's assembly line ---- *Pipeline hazard:* the next instruction can't execute on the following clock cycle  - *Structural hazard*: two or more instructions need the same part of CPU - *Data hazard*: need to wait for operands to be computed from a previous step - *Control hazard*: the CPU can't tell which instructions it needs to execute next **^ requires a pipeline flush on branch misprediction** <!-- .element: class="fragment" data-fragment-index="1" --> --- ## Predication ---- `c = max(a, b)` ---- `c = (a > b ? a : b)` ---- `c = (a > b) * a + (a <= b) * b` ---- `c = (a > b) * (a - b) + b` ---- `c = ((b - a) >> 31) * (a - b) + b` ---- ```nasm cmp eax, ebx cmovg ebx, eax ; if eax > ebx, ebx := eax ``` --- ## Removing branches ---- ```cpp int lower_bound(int x) { int l = 0, r = n - 1; while (l < r) { int m = (l + r) / 2; if (t[m] >= x) r = m; else l = m + 1; } return t[l]; } ``` ---- ```cpp int lower_bound(int x) { int *base = t, len = n; while (len > 1) { int half = len / 2; if (base[half] < x) { base += half; len = len - half; } else { len = half; } } return t[l]; } ``` ---- ```cpp int lower_bound(int x) { int *base = t, len = n; while (len > 1) { int half = len / 2; if (base[half] < x) base += half; len -= half; // len = ceil(len / 2) works either way } return t[l]; } ``` ---- ```cpp int lower_bound(int x) { int *base = t, len = n; while (len > 1) { int half = len / 2; base = (base[half] < x ? &base[half] : base); // replaced with a "cmov" len -= half; } return *(base + (*base < x)); } ``` <!-- todo: last line only for the last iteration? --> **Exactly** $\lceil \log_2 n \rceil$ iterations, so not strictly equivalent to binary search <!-- .element: class="fragment" data-fragment-index="1" --> ----  Why worse on larger arrays? <!-- .element: class="fragment" data-fragment-index="1" --> *Prefetching (speculation)* <!-- .element: class="fragment" data-fragment-index="2" --> ---- ```cpp int lower_bound(int x) { int *base = t, len = n; while (len > 1) { int half = len / 2; __builtin_prefetch(&base[(len - half) / 2]); __builtin_prefetch(&base[half + (len - half) / 2]); base = (base[half] < x ? &base[half] : base); len -= half; } return *(base + (*base < x)); } ``` ----  Still grows slightly faster as the branchy version prefetches more descendants --- ## Cache locality ---- - Memory is split into 64B blocks called *cache lines* - When we (pre-)fetch a single byte, we fetch the entire cache line ----  - *Spatial locality*: only okay for the last 3-4 requests <!-- .element: class="fragment" data-fragment-index="1" --> - *Temporal locality*: only okay for the first dozen or so requests <!-- .element: class="fragment" data-fragment-index="2" --> ---- ```cpp int lower_bound(int x) { int l = 0, r = n - 1; while (l < r) { int m = l + rand() % (r - l); if (t[m] >= x) r = m; else l = m + 1; } return t[l]; } ``` ----  ~6x slower of larger arrays, although theoretically should only perform $\frac{2 \ln n}{\log_2 n} = 2 \ln 2 \approx 1.386$ more comparisons ----  ----  Hot and cold elements are grouped together --- **Michaël Eytzinger** is a 16th-century Austrian nobleman known for work on genealogy ----  *Ahnentafel* (German for "ancestor table") ---- - First, the person themselves is listed as number 1 - Then, recursively, for each person numbered $k$, their father is listed as $2k$, and their mother is listed as $(2k+1)$ ---- Example for **Paul I**, the great-grandson of **Peter the Great**: 1. Paul I 2. Peter III (Paul’s father) 3. Catherine II (Paul’s mother) 4. Charles Frederick (Peter’s father, Paul’s paternal grandfather) 5. Anna Petrovna (Peter’s mother, Paul’s paternal grandmother) 6. Christian August (Catherine’s father, Paul’s maternal grandfather) 7. 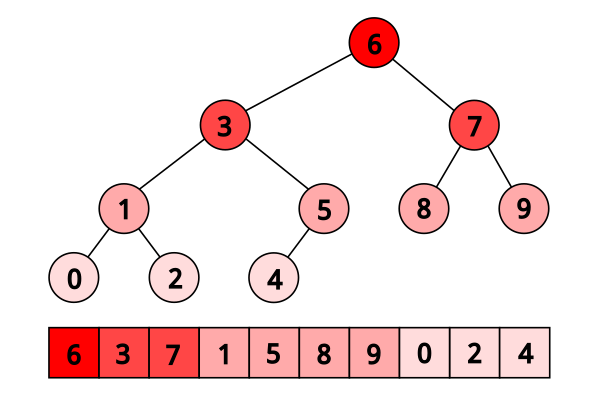Johanna Elisabeth (Catherine’s mother, Paul’s maternal grandmother) Peter the Great's bloodline is: Paul I → Peter III → Anna Petrovna → Peter the Great, so his number should be $((1 \times 2) \times 2 + 1) \times 2 = 10$ <!-- .element: class="fragment" data-fragment-index="5" --> ----  This enumeration has been widely used for implicit implementations of heaps, segment trees, and other binary tree structures ----   Temporal locality is much better --- ### Building ---- ```cpp int a[n], t[n + 1]; // the original sorted array and the eytzinger array we build // ^ we need one element more because of one-based indexing void eytzinger(int k = 1) { static int i = 0; if (k <= n) { eytzinger(2 * k); t[k] = a[i++]; eytzinger(2 * k + 1); } } ``` - Depth is $O(\log n)$ since we double $k$ each time we descend - We write exactly $n$ elements (`if` is entered exactly once for each $k$ from $1$ to $n$) - We write sequential elements from the original array (`i` incremented each time) - By the time we write the element at node $k$, we will have already written all its preceding elements (exactly `i` of them) ---- ### Searching ---- Instead of ranges, start with $k=1$ and execute until $k < n$: - If $x < a_k$, go left: $k := 2k$ - Otherwise, go right: $k := 2k + 1$ ---- ``` array: 1 2 3 4 5 6 7 8 eytzinger: 5 3 7 2 4 6 8 1 1st range: --------------- k := 1 2nd range: ------- k := 2*k (=2) 3rd range: --- k := 2*k + 1 (=5) 4th range: - k := 2*k (=10) ``` - Unless the answer is the last element, we compare $x$ against it at some point - After we learn that $ans \geq x$, we start comparing $x$ against elements to the left - All these comparisons will evaluate true ("leading to the right") - $\implies$ We need to "cancel" some number of right turns <!-- .element: class="fragment" data-fragment-index="1" --> ---- ```cpp int lower_bound(int x) { int k = 1; while (k <= n) k = 2 * k + (t[k] < x); k >>= __builtin_ffs(~k); return t[k]; } ``` - Right-turns are recorded in the binary notation of $k$ as 1-bits - Right-shift $k$ by the number of trailing ones in its binary notation - To find it, we can invert the bits of $k$ and use "find first set" instruction ----  Worse than branchless on large arrays because the last 3-4 iterations are not cached --- ## Prefetching ---- ```cpp alignas(64) int t[n + 1]; // allocate the array on the beginning of a cache line int lower_bound(int x) { int k = 1; while (k <= n) { __builtin_prefetch(t + k * 16); k = 2 * k + (t[k] < x); } k >>= __builtin_ffs(~k); return t[k]; } ``` What is happening? What is $k \cdot B$? It is $k$'s great-great-grandfather! <!-- .element: class="fragment" data-fragment-index="1" --> ---- - When we fetch $k \cdot B$, we also fetch its $(B - 1)$ cache line neighbors - If the array is **aligned**, they will all be our grandfathers - As i/o is pipelined, we are always prefetching 4 levels in advance  ----  ---  What are these bumps? ---- ```cpp t[0] = -1; // an element that is less than x iters = std::__lg(n + 1); int lower_bound(int x) { int k = 1; for (int i = 0; i < iters; i++) k = 2 * k + (t[k] < x); int *loc = (k <= n ? t + k : t); k = 2 * k + (*loc < x); k >>= __builtin_ffs(~k); return t[k]; } ``` ----  --- - In Eytzinger binary search, we trade off **bandwidth** for **latency** with prefetching - Doesn't work well in bandwidth-constrained environments (multi-threading) - Instead, we can fetch fewer cache lines ---- ## B-trees ---- $B \ge 2$ keys in each node, increasing branching factor and reducing tree height ----  A B-tree of order 4 ---- - For RAM, set $B$ to be the cache line size so that we don't waste reads - $B=16$ reduces the tree height by $\frac{\log_2 n}{\log_17 n} = \frac{\log 17}{\log 2} = \log_2 17 \approx 4.09$ times ---- We can make static B-trees **implicit** by generalizing the Eytzinger numeration: - The root node is numbered $0$ - Node $k$ has $(B + 1)$ child nodes numbered $\{k \cdot (B + 1) + i + 1\}$ for $i \in [0, B]$ ---- ```cpp const int B = 16; int nblocks = (n + B - 1) / B; int btree[nblocks][B]; int go(int k, int i) { return k * (B + 1) + i + 1; } ``` ---- ```cpp void build(int k = 0) { static int t = 0; if (k < nblocks) { for (int i = 0; i < B; i++) { build(go(k, i)); btree[k][i] = (t < n ? a[t++] : INT_MAX); } build(go(k, B)); } } ``` --- ### Searcihng ----  Zen 2 supports AVX2, so we can compare $256/32=8$ keys at a time ---- ```cpp int mask = (1 << B); for (int i = 0; i < B; i++) mask |= (btree[k][i] >= x) << i; int i = __builtin_ffs(mask) - 1; // now i is the number of the correct child node ``` ---- ```cpp typedef __m256i reg; int cmp(reg x_vec, int* y_ptr) { reg y_vec = _mm256_load_si256((reg*) y_ptr); // load 8 sorted elements reg mask = _mm256_cmpgt_epi32(x_vec, y_vec); // compare against the key return _mm256_movemask_ps((__m256) mask); // extract the 8-bit mask } ``` ---- ```cpp int mask = ~( cmp(x, &btree[k][0]) + (cmp(x, &btree[k][8]) << 8) ); int i = __builtin_ffs(mask) - 1; k = go(k, i); ``` Familiar problem: a local lower bound doesn't have to exist in the leaf node <!-- .element: class="fragment" data-fragment-index="1" --> ---- ```cpp int lower_bound(int _x) { int k = 0, res = INT_MAX; reg x = _mm256_set1_epi32(_x); while (k < nblocks) { int mask = ~( cmp(x, &btree[k][0]) + (cmp(x, &btree[k][8]) << 8) ); int i = __builtin_ffs(mask) - 1; if (i < B) res = btree[k][i]; k = go(k, i); } return res; } ``` ---- > "The more you think about what the B in B-trees means, the better you understand B-trees" - **B-tree**: balanced, broad, bushy, Boeing, Bayer - **S-tree**: static, succinct, speedy, SIMDized <!-- .element: class="fragment" data-fragment-index="1" --> ----  --- ### Optimizations ---- #1: Hugepages ---- ```cpp const int P = 1 << 21; // page size in bytes (2MB) const int T = (64 * nblocks + P - 1) / P * P; // can only allocate whole number of pages btree = (int(*)[16]) std::aligned_alloc(P, T); madvise(btree, T, MADV_HUGEPAGE); ``` ----  (No significant effect for implementations with some form of prefetching) ---- #2: Make the # of iterations compile-time constant ---- ```cpp constexpr int height(int n) { // grow the tree until its size exceeds n elements int s = 0, // total size so far l = B, // size of the next layer h = 0; // height so far while (s + l - B < n) { s += l; l *= (B + 1); h++; } return h; } const int H = height(N); ``` ---- #3: Better local lower_bound (`movemask` is relatively slow) ---- ```cpp unsigned rank(reg x, int* y) { reg a = _mm256_load_si256((reg*) y); reg b = _mm256_load_si256((reg*) (y + 8)); reg ca = _mm256_cmpgt_epi32(a, x); reg cb = _mm256_cmpgt_epi32(b, x); reg c = _mm256_packs_epi32(ca, cb); // combines vector masks int mask = _mm256_movemask_epi8(c); // we need to divide the result by two because we call movemask_epi8 on 16-bit masks: return __tzcnt_u32(mask) >> 1; } ``` ---- ```cpp void permute(int *node) { const reg perm = _mm256_setr_epi32(4, 5, 6, 7, 0, 1, 2, 3); reg* middle = (reg*) (node + 4); reg x = _mm256_loadu_si256(middle); x = _mm256_permutevar8x32_epi32(x, perm); _mm256_storeu_si256(middle, x); } ``` ---- ```cpp unsigned rank(reg x, int* y) { reg a = _mm256_load_si256((reg*) y); reg b = _mm256_load_si256((reg*) (y + 8)); reg ca = _mm256_cmpgt_epi32(a, x); reg cb = _mm256_cmpgt_epi32(b, x); reg c = _mm256_packs_epi32(ca, cb); int mask = _mm256_movemask_epi8(c); return __builtin_popcount(mask) >> 1; // popcnt does not need specific bit order } ``` ---- ```cpp int lower_bound(int _x) { int k = 0, res = INT_MAX; reg x = _mm256_set1_epi32(_x - 1); for (int h = 0; h < H - 1; h++) { unsigned i = rank(x, &btree[k]); update(res, &btree[k], i); k = go(k, i); } // the last branch: if (k < nblocks) { unsigned i = rank(x, btree[k]); update(res, &btree[k], i); } return res; } ``` ----  ---- ```cpp int lower_bound(int _x) { int k = 0, res = INT_MAX; reg x = _mm256_set1_epi32(_x - 1); for (int h = 0; h < H - 1; h++) { unsigned i = rank(x, &btree[k]); update(res, &btree[k], i); k = go(k, i); } // the last branch: if (k < nblocks) { unsigned i = rank(x, btree[k]); update(res, &btree[k], i); } return res; } ``` - The `update` procedure is unnecessary 16 times out of 17 - We perform a non-constant number of iterations, causing pipeline stalls --- ## B+ trees ---- - *Internal nodes* store up to $B$ keys and $(B + 1)$ pointers to child nodes - *Data nodes* or *leaves* store up to $B$ keys, the pointer to the next leaf node - Keys are *copied* to upper layers (the structure is **not** succinct) ----  A B+ tree of order 4 ---- - The last node or its next neighbor has the local lower bound (no `update`) - The depth is constant because B+ trees grow at the root (no branching) ---- ```cpp // the height of a balanced n-key B+ tree constexpr int height(int n) { /* ... */ } // where the layer h starts (data layer is numbered 0) constexpr int offset(int h) { /* ... */ } const int H = height(N); const int S = offset(H); // ... quite a bit of code to build the tree skipped ... ``` ---- ```cpp int lower_bound(int _x) { unsigned k = 0; // we assume k already multiplied by B to optimize pointer arithmetic reg x = _mm256_set1_epi32(_x - 1); for (int h = H - 1; h > 0; h--) { unsigned i = rank(x, btree + offset(h) + k); k = k * (B + 1) + i * B; } unsigned i = rank(x, btree + k); return btree[k + i]; } ``` ---  (Spikes at the end due to L1 TLB spill) ----  ----  --- - Non-uniform block sizes - Grouping layers together - Selective prefetching - Non-temporal reads - Reversing the order of layers - `blend` / `packs` - `popcount` / `tzcnt` - Defining key $i$ as *maximum* on subtree $i$ - Rewriting the whole thing in assembly ---- To measure *reciprocal throughput*: ```cpp clock_t start = clock(); for (int i = 0; i < m; i++) checksum ^= lower_bound(q[i]); float seconds = float(clock() - start) / CLOCKS_PER_SEC; printf("%.2f ns per query\n", 1e9 * seconds / m); ``` To measure *real* latency: ```cpp int last = 0; for (int i = 0; i < m; i++) { last = lower_bound(q[i] ^ last); checksum ^= last; } ``` ----  ----  ----  --- As a *dynamic* tree? ----  --- ## B− Tree ---- ```cpp int *tree; // internal nodes store (B - 2) keys followed by (B - 1) pointers; leafs store (B - 1) keys int lower_bound(int _x) { unsigned k = root; reg x = _mm256_set1_epi32(_x); for (int h = 0; h < H - 1; h++) { unsigned i = rank(x, &tree[k]); k = tree[k + B + i]; // fetch next pointer } unsigned i = rank(x, &tree[k]); return tree[k + i]; } ``` ---- ```cpp struct Precalc { alignas(64) int mask[B][B]; constexpr Precalc() : mask{} { for (int i = 0; i < B; i++) for (int j = i; j < B - 1; j++) // everything from i to B - 2 inclusive needs to be moved mask[i][j] = -1; } }; constexpr Precalc P; void insert(int *node, int i, int x) { // need to iterate right-to-left to not overwrite the first element of the next lane for (int j = B - 8; j >= 0; j -= 8) { // load the keys reg t = _mm256_load_si256((reg*) &node[j]); // load the corresponding mask reg mask = _mm256_load_si256((reg*) &P.mask[i][j]); // mask-write them one position to the right _mm256_maskstore_epi32(&node[j + 1], mask, t); } node[i] = x; // finally, write the element itself } ``` ----  ----  ----