Olympiad 2024. Arithmetics
---
[TOC]
# Для разогрева
## 1. [Простая задача. Фибоначчи](https://www.eolymp.com/ru/problems/4730)

## 2. Задача, связанная с арифметикой и как-то с геометрией. [Числа Фибоначчи](https://www.eolymp.com/ru/problems/5197)
<details>
<summary>Подсказка 1</summary>

</details>
<details>
<summary>Подсказка 2</summary>

### 2.1 Простая тренировочная задача- объяснение
[Быстрое возведение в степень](https://www.eolymp.com/ru/problems/2814)


### 2.2 Классическая тренировочная задача
```c++=1
void muliplyMatrix(int a1, int b1,
int c1, int d1,
int a2, int b2,
int c2, int d2,
int& a3, int& b3,
int& c3, int& d3
)
{
a3 = a1*a2 + b1*c2;
b3 = a1*b2 + b1*d2;
c3 = c1*a2 + d1*c2;
d3 = c1*b2 + d1*d2;
}
```
[Возведение в степень](https://www.eolymp.com/ru/problems/273)
</details>
# [Системы счисления](https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F)
## [Фибоначчиева система счисления](https://www.eolymp.com/ru/problems/1378)
<img src=https://hackmd.io/_uploads/B1Z0lb0h6.png width=300>
<h2>Я не знаю языка MarkDown!</h2>
<h4>Это не страшно. Большая часть HTML является подмножеством MarkDown</h4>
## Получение и распечатка слева направо двоичных цифр числа n
В решении этой задачи используется рекурсия
```c++=10
void printBinary(int n){
if(n==0) return;
printBinary(n/2);
cout<<n%2;
}
```
## [Игра НИМ и двоичная система счисления](https://www.eolymp.com/ru/problems/1011)
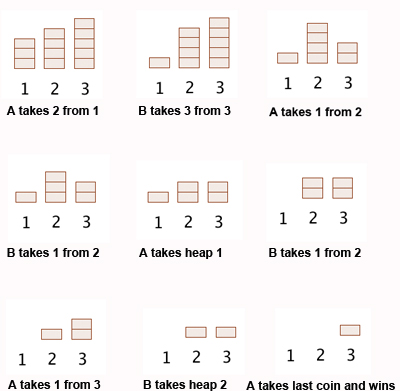
```nim
Запишем числа игры НИМ в двоичной системе счисления:
001=1 011=3
100=4 100=4
101=5 101=5
----- -----
000 010=2 = (3 xor 4 xor 5) - неравновесие
0=(1 xor 4 xor 5) -равновесие!
```
```nim
111=7
111=7
111=7
-----
111=7 = (7 xor 7 xor 7) -неравновесие
000=0
111=7
111=7
---
000=0 = (0 xor 7 xor 7) -равновесие!
```
[Тренировочная задача. Ним](https://www.eolymp.com/ru/problems/1011)
# Основная теорема арифметики

## Количество делителей

```c++
2^2 3^2 2^2 * 3^2 = 36
--- ---
2^0 3^0
2^1 3^1
2^2 3^2
--- ---
3 * 3 = 9 -- количество делителей числа 36 (включая 1)
```
```c++
2^3 3^2 5^1 2^3 * 3^2 * 5^1 = 360
--- --- ---
2^0 3^0 5^0
2^1 3^1 5^1
2^2 3^2
2^3
--- --- ---
4 * 3 * 2 = 24 -- количество делителей числа 360 (включая 1)
```
[Количество делителей](https://www.eolymp.com/ru/problems/2862)
## Все делители
[Все делители](https://www.eolymp.com/ru/problems/8669)
[Решето Эратосфена](https://www.eolymp.com/ru/problems/4739)

## Сумма делителей
[Сумма делителей](https://www.eolymp.com/ru/problems/1782)
# Алгоритм Евклида

```Factorizing
Разлагая на множители (трудозатратная операция):
36 = 2 * 2 * 3 * 3
24 = 2 * 2 * 2 * 3,
получаем наибольший общий делитель:
GCD(36,24) = 2 * 2 * 3 = 12.
```
```euclid
Используя многократное вычитание (лучше остаток от деления):
{//By Euclid
36 % 24 = 12
24 % 12 = 0
},
получаем наибольший общий делитель:
GCD(36,24) = 12
```
https://www.eolymp.com/ru/problems/413
https://www.eolymp.com/ru/problems/136

## Дерево отрезков в памяти
Пусть массив $a$ имеет $n$ элементов:
$$
a[0],a[1],\dots ,a[n-1] .
$$
Выберем $h$ такое, что $2^h\geq n$.
Дополним наш массив справа нейтральными элементами так, чтобы его длина равнялась $2^h$. Тогда для хранения дерева отрезков, построенного на элементах массива $a$, нам понадобится массив $b$ из $2^{h+1}$ ячеек.
Нулевую ячейку в массиве $b$ мы использовать не будем, а ячейки с первой по
$(2^{h+1}-1)$-ю будут соответствовать вершинам двоичного дерева с соответствующими номерами.
Обычно используется нумерация вершин дерева отрезков в порядке обхода в ширину, то есть корень дерева имеет номер 1, а левый и правый сыновья вершины с номером $v$ имеют номера $2v$ и $2v+1$ соответственно. При такой нумерации вершина с номером $2^k+u$ при $0\leq u<2^k$ будет соответствовать отрезку $[u2^{h-k}; (u+1)2^{h-k}-1]$.
То есть, в ячейке $b[2^{k}+u]$ будет храниться число
$f(a[u2^{h-k}],a[u2^{h-k}+1],\dots ,a[(u+1)2^{h-k}-1])$.
```graphviz
digraph hierarchy {
nodesep=1.0 // increases the separation between nodes
node [color=Red,fontname=Courier,shape=circle]
edge [color=Blue, style=dashed]
1-> {2 3}
2->{4 5}
3->{6 7}
4 -> {8 9}
5 -> {10 11}
6 -> {12 13}
7 -> {14 15}
1 [xlabel="[0......7]"]
2 [xlabel="[0..3]"]
4 [xlabel="[0 1]"] 8 [xlabel="[0]"] 9 [xlabel="[1]"]
5 [xlabel="[2 3]"] 10 [xlabel="[2]"] 11 [xlabel="[3]"]
3 [xlabel="[4..7]"]
6 [xlabel="[4 5]"] 12 [xlabel="[4]"] 13 [xlabel="[5]"]
7 [xlabel="[6 7]"] 14 [xlabel="[6]"] 15 [xlabel="[7]"]
{rank=same;4 5 6 7} // Put them on the same level
}
```
Далее будет использоваться именно такая нумерация вершин дерева отрезков. В качестве альтернативы можно нумеровать вершины в порядке обхода в глубину, тогда левый и правый сыновья вершины $v$ будут иметь номера:
$v+1$
и
$v+2(\lfloor {\dfrac {L+R}{2}}\rfloor -L+1)$,
где $[L;R]$ — отрезок, соответствующий вершине $v$.
При этом, если строить дерево отрезков сразу по исходному массиву $a$, а не расширять его до длины $2^h$ (в таком дереве не все длины отрезков будут степенями двойки и не все листья будут расположены на максимальной глубине), то для его хранения будет достаточно всего $2n$ ячеек в массиве $b$.
При хранении же дерева, вершины которого занумерованы в порядке обхода в ширину, длина массива $b$ может достигать $4n-4$.