<style>
.reveal .slides {
text-align: left;
font-size:28px;
}
</style>
# 生成式AI與機率論
----
- 生成對抗網路(GAN)
- Transformer模型
- 自回歸卷積神經網路(AR- CNNs)
- 貝氏網路(Bayesian Network)
- 高斯混合模型(GMM)
- 隱馬爾可夫模型(HMM)
- 隱含狄利克雷分布(LDA)
- 變分自編碼器 (VAEs)
---
# Bayesian Network
## 貝氏網路
----
是一種表示變數之間條件相依性的概率模型
它是以有向無環圖(DAG)的形式呈現的,其中節點表示隨機變數,邊表示變數之間的條件相依性
---
# Conditional Probability
## 條件機率
## $P(A|B) = \frac{P(A \cap B)}{P(B)}$
----
# Bayes' Rule
## 貝氏定理
## $P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$
----
# Joint Probability
## 聯合機率
----
### C = 早上有雲的機率
|C = cloud|C = ¬cloud|
|:-------:|:--------:|
| 0.4 | 0.6 |
### R = 下午下雨的機率
|R = rain|R = ¬rain|
|:-------:|:--------:|
| 0.1 | 0.9 |
----
| |R = rain|R = ¬rain|
|:--------:|:------:|:-------:|
|C = cloud | 0.08 | 0.32 |
|C = ¬cloud| 0.02 | 0.58 |
----
## 下午下雨時早上有雲機率?
## $P(C|rain) = \frac{P(C,rain)}{P(rain)}$
----
## $\frac{P(C,rain)}{P(rain)} = \alpha\cdot P(C,rain) = \alpha\cdot<0.08, 0.02>$
----
## Normalize
## $P(C|rain) = <0.8, 0.2>$
---
## Bayesian Network
Bayesian Network是一種表示隨機變量之間依賴關係的數據結構。
Bayesian Network具有以下特性:
1. 它們是有向圖
2. 圖上的每個節點代表一個隨機變數
3. 從 X 到 Y 的箭頭表示 X 是 Y 的父節點。換句話說,Y 的概率分佈取決於 X 的值
4. 每個節點 X 具有概率分佈 P(X | Parents(X)),即給定其父節點的條件下 X 的概率分佈
----
## 是否會錯過會議

----
## 下雨的機率
| none | light | heavy |
|------|-------|-------|
| 0.7 | 0.2 | 0.1 |
----
| R | yes | no |
|-------|------|------|
| none | 0.4 | 0.6 |
| light | 0.2 | 0.8 |
| heavy | 0.1 | 0.9 |
Maintenance表示是否進行火車軌道的維護。
Rain是Maintenance的父節點,這意味著Maintenance的概率分佈受到Rain影響
----
| R | M | on time | delay |
|:-----:|:----:|:-------:|:-----:|
| none | yes | 0.8 | 0.2 |
| none | no | 0.9 | 0.1 |
| light | yes | 0.6 | 0.4 |
| light | no | 0.7 | 0.3 |
| heavy | yes | 0.4 | 0.6 |
| heavy | no | 0.5 | 0.5 |
----
| T | attend | miss |
|----------|--------|------|
| on time | 0.9 | 0.1 |
| delayed | 0.6 | 0.4 |
----
如果我們想找出在沒有維護且下著小雨的一天火車晚點時錯過會議的機率,可以表達成:
$P(light, no, delayed, miss)$
----
計算:
$P(light)P(no | light)P(delayed | light, no)P(miss | delayed)$
$=0.2\cdot 0.8\cdot 0.3\cdot 0.4$
----
# Inference by Enumeration
## $P(X|e) = \alpha P(X, e) = \alpha\sum_{y}\limits {P(X, e, y)}$
$X$ (查詢變數)
$e$ (觀察到的證據)
$y$ (隱藏變數的所有值)
$\alpha$ (normalize參數)
---
# Project
## 計算 [GJB2 gene](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1285178/) 與聽力受損的關係
----
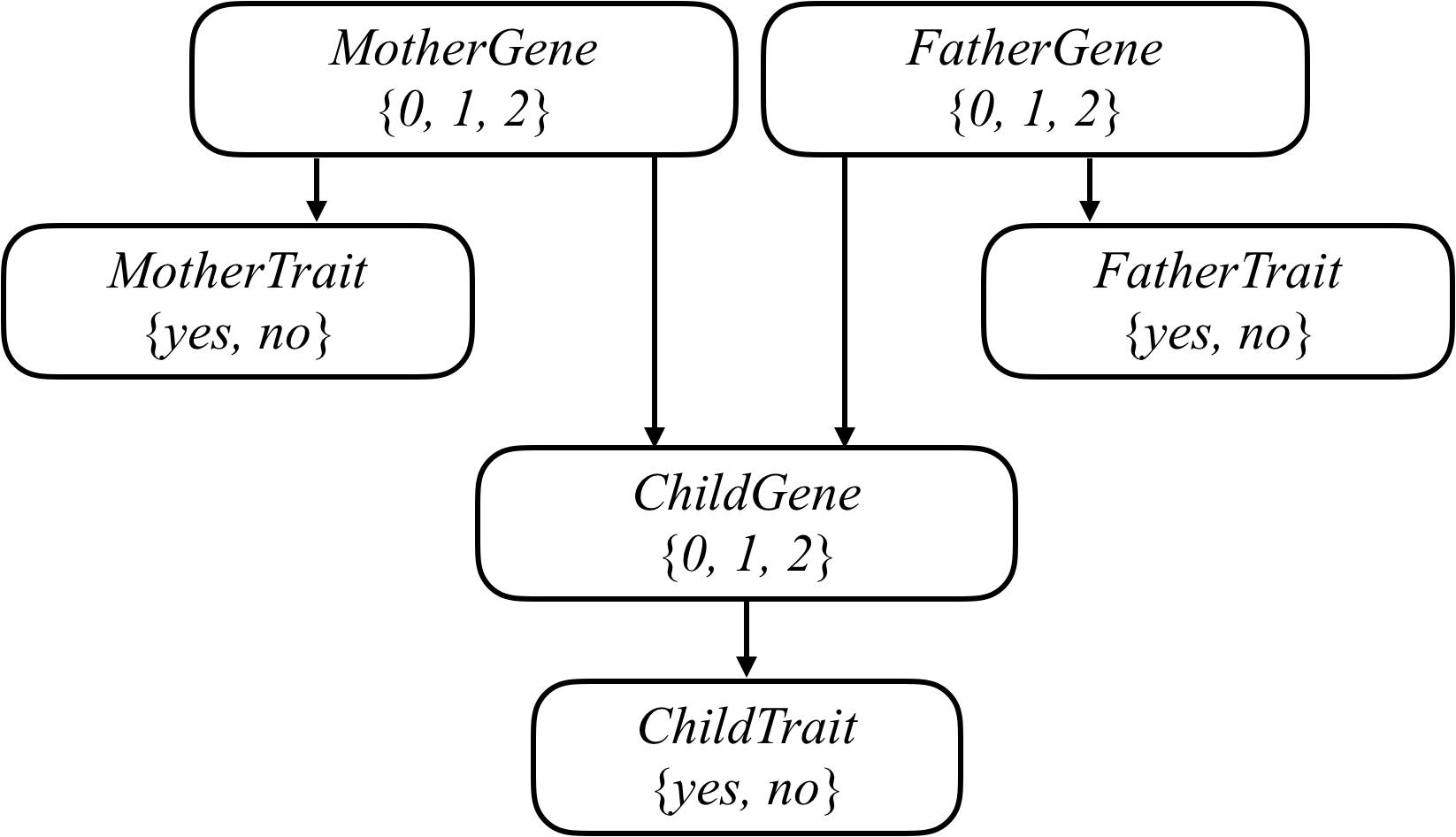
## GJB2 gene
GJB2 gene 的突變版本是新生兒聽力損傷的主要原因之一
每個人都有可能擁有 **0、1 或 2** 個聽力損傷版本的 GJB2 gene
----
| Gene | Probability |
|:----:|:-----------:|
| 2 | 0.01 |
| 1 | 0.03 |
| 0 | 0.96 |
----
| Gene | Trait True | Trait False |
|:-----------:|:-----------------:|:-----------------:|
| 2 | 0.65 | 0.35 |
| 1 | 0.56 | 0.44 |
| 0 | 0.01 | 0.99 |
----
| Mutation |
|:--------:|
| 0.01 |
----
<!-- .slide: data-background="#FFFFFF" -->
----
## 計算聯合機率
```py
def joint_probability(people, one_gene, two_genes, have_trait):
"""
Compute and return a joint probability.
The probability returned should be the probability that
* everyone in set `one_gene` has one copy of the gene, and
* everyone in set `two_genes` has two copies of the gene, and
* everyone not in `one_gene` or `two_gene` does not have the gene, and
* everyone in set `have_trait` has the trait, and
* everyone not in set` have_trait` does not have the trait.
"""
ret = 1
for person in people:
# Determine how many genes the person has
genes = genes_number(person, one_gene, two_genes)
# Determine the probability of the person having the gene
if people[person]["mother"] is None and people[person]["father"] is None:
ret *= PROBS["gene"][genes]
else:
father = inherit_probability(people[person]["father"], one_gene, two_genes)
mother = inherit_probability(people[person]["mother"], one_gene, two_genes)
if genes == 2:
ret *= father * mother
elif genes == 1:
ret *= (father * (1 - mother) + mother * (1 - father))
else:
ret *= (1 - father) * (1 - mother)
# Determine the probability of the person having the trait
ret *= PROBS["trait"][genes][person in have_trait]
return ret
```
----
## 將算出的聯合機率更新
```py
def update(probabilities, one_gene, two_genes, have_trait, p):
"""
Add to `probabilities` a new joint probability `p`.
Each person should have their "gene" and "trait" distributions updated.
Which value for each distribution is updated depends on whether
the person is in `have_gene` and `have_trait`, respectively.
"""
for person in probabilities:
genes = genes_number(person, one_gene, two_genes)
probabilities[person]["gene"][genes] += p
probabilities[person]["trait"][person in have_trait] += p
```
----
## Normalize 函數
```py
def normalize(probabilities):
"""
Update `probabilities` such that each probability distribution
is normalized (i.e., sums to 1, with relative proportions the same).
"""
for person in probabilities:
# Normalize the gene probabilities
sum = 0
for gene in probabilities[person]["gene"]:
sum += probabilities[person]["gene"][gene]
for gene in probabilities[person]["gene"]:
probabilities[person]["gene"][gene] /= sum
# Normalize the trait probabilities
sum = 0
for trait in probabilities[person]["trait"]:
sum += probabilities[person]["trait"][trait]
for trait in probabilities[person]["trait"]:
probabilities[person]["trait"][trait] /= sum
```
----
## 執行結果
```bash
$python heredity.py ./data/family0.csv
Harry:
Gene:
2: 0.0092
1: 0.4557
0: 0.5351
Trait:
True: 0.2665
False: 0.7335
James:
Gene:
2: 0.1976
1: 0.5106
0: 0.2918
Trait:
True: 1.0000
False: 0.0000
Lily:
Gene:
2: 0.0036
1: 0.0136
0: 0.9827
Trait:
True: 0.0000
False: 1.0000
```
[完整程式碼](https://github.com/AnthonyQwO/CS50AI/tree/main/Project2/heredity)
----
## Family 0
| name | mother | father | trait |
|:-----:|:------:|:------:|:-----:|
| Harry | Lily | James | |
| James | | | 1 |
| Lily | | | 0 |
---
## 參考資料
- https://outlook.stpi.narl.org.tw/index/focus-news/4b11410088212dac0188748d1c2f44a7
- https://www.youtube.com/watch?v=D8RRq3TbtHU&t=4351s
- https://cs50.harvard.edu/ai/2024/notes/2/
- https://cs50.harvard.edu/ai/2024/projects/2/heredity/
{"contributors":"[{\"id\":\"3fcc501a-fe31-44df-b14c-56df5e53a777\",\"add\":7842,\"del\":479}]","title":"BayesianNetwork","description":"Bayesian Network."}