# Big O Notation --- - Describe big-O notation - Evaluate the runtime of algorithms using big-O notation - Compare fastest to slowest asymptotic complexities of common runtimes (e.g. O(1), O(log(n)), O(n), O(nlog(n)), O(n^2), etc). - Explain the difference between time complexity and space complexity --- ## Algorithm Performance - Good to know how fast something is - Lots of variables - can't just time things --- ## Big O Notation: Background - theoretical way of comparing algorithms - approximate upper bound --- ## Big O Notation 1. Constants are ignored 2. Smaller components are ignored --- O(500 * n) --> O(n) O(99999999999) --> O(1) O(10*n^2 + 5n + 20) --> O(n^2) O(n * n) --> O(n^2) O(n*log(n) + 30000 * n) --> O(n * log(n)) --- ## Examples Big O Runtimes --- ### O(1) ```js function add(num1, num2, num3) { return num1 + num2 + num3; } ``` --- ```js function sayHello() { for (var i = 0; i < 100; i++) { console.log("Hello"); } } ``` ```js function logMultiples(num) { for (var i = 0; i < 10; i++) { console.log(i * num); } } ``` --- ### O(n) The following algorithms are O(n), or linear time, because the data set is iterated over approximately one time --- ```js function sayHello(numberOfTimes) { for (var i = 0; i < numberOfTimes; i++) { console.log("Hello"); } } ``` --- ```js function doubleThenTriple(numbers) { var doubled = numbers.map(function(num) { return num * 2; }); return doubled.map(function(num) { return num * 3; }); } ``` --- **What matters is that the runtime scales in proportion to the input size, not the details of the proportional relationship.** --- ### O(n^2) ```js function allPairs(arr) { var pairs = []; for (var i = 0; i < arr.length; i++) { for (var j = i + 1; j < arr.length; j++) { pairs.push([arr[i], arr[j]]); } } return pairs; } ``` --- ```js function bubbleSort(arr) { var len = arr.length; var lastSwap; var temp while (len != 0) { lastSwap = 0; for (var i = 1; i < len; i++) { if (arr[i - 1] > arr[i]) { // Swap the two elements temp = arr[i-1]; arr[i-1] = arr[i]; arr[i] = temp; lastSwap = i; } } len = lastSwap; } } ``` --- In these two examples, within each element of the array, we are iterating over all elements again. Therefore, the runtime is O(n * n) or O(n2). --- Rule of thumb: - If you see nested loops, the runtime will be O(nlevels of nesting). --- ### But not always! --- ```js function logMultiples(n) { for (var num1 = 1; num1 <= n; num1++) { for (var num2 = 1; num2 <= n; num2++) { console.log(num1 * num2); } } } ``` --- ```js function logSomeMultiples(n) { for (var num1 = 1; num1 < n; num1++) { for (var num2 = 1; num2 <= Math.min(n, 10); num2++) { console.log(num1 * num2); } } } ``` --- ### make sure to check the loops runtime --- ## Comparing Common Big O Runtimes ---  - 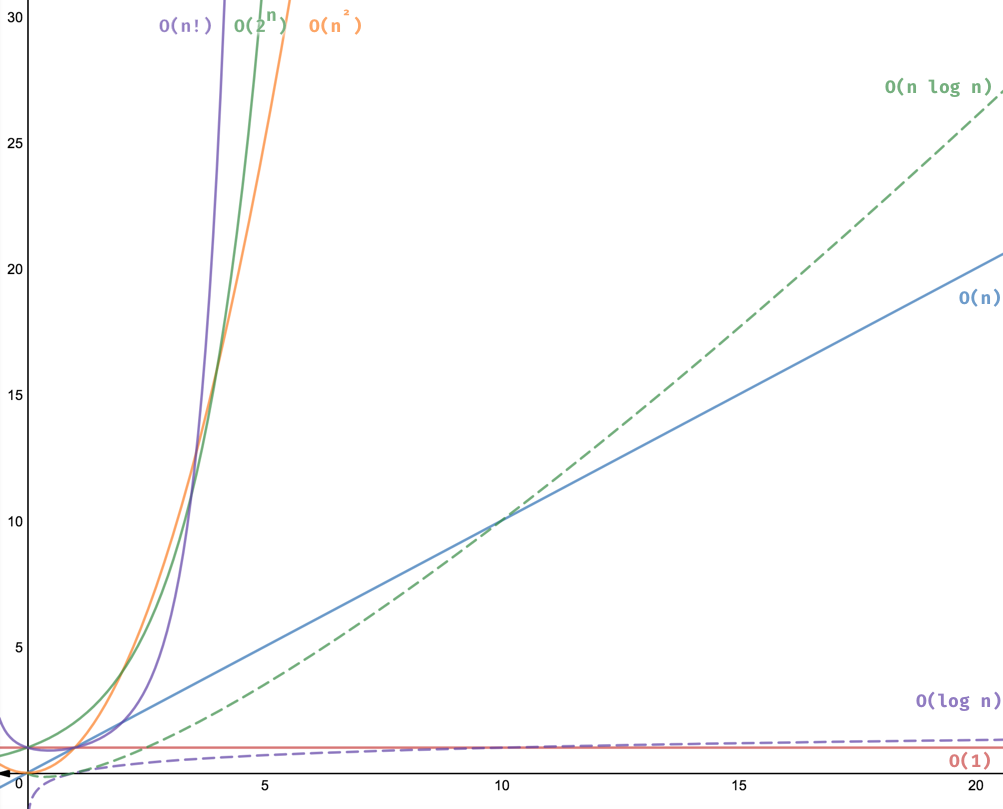What are the colours --- ### Across Time and Space - So far we've only been talking about the runtime - But Big O isn't just used to talk about the time it takes our programs to run - it's also used to talk about how much space (i.e. memory) our program requires. --- - Very often we're concerned primarily with **auxiliary space complexity** - _how much additional memory does the algorithm require beyond what needs to be allocated for the inputs themselves?_ --- ```js function total(array) { var total = 0; for (var i = 0; i < array.length; i++) { total += array[i]; } return total; } ``` --- - one input, array - time complexity = O(n) - Space complexity? --- - O(1) - For total --- ```js function double(array) { var newArray = []; for (var i = 0; i < array.length; i++) { newArray.push(2 * array[i]); } return newArray; } ``` --- - Space complexity = O(n) - Need a unit of memory for each element of the array