# Modelado de Flujos
### Prerrequisitos:

- [Definición de red de flujo y flujo máximo](https://cp-algorithms.com/graph/edmonds_karp.html)
- Algoritmos para hallar el flujo máximo:
-- [Ford-Fulkerson - $O(f|E|)$](https://cp-algorithms.com/graph/edmonds_karp.html#ford-fulkerson-method)
-- [Edmonds-Karp - $O(|V||E|^2)$](https://cp-algorithms.com/graph/edmonds_karp.html#edmonds-karp-algorithm)
-- [Dinic - $O(|V|^2|E|)$](https://cp-algorithms.com/graph/dinic.html)

## Máximo emparejamiento bipartito (maximum bipartite matching)
### Definiciones
#### Emparejamiento en un grafo
Dado un grafo $G=(V,E)$, un emparejamiento es un subconjunto $M$ del conjunto aristas $E$, donde cada par de aristas de $M$ es no-adyacente, o en otras palabras, cada nodo $u$ del conjunto de nodos $V$ es adyacente a lo más una arista de $M$.

#### Emparejamiento máximo
Dado un grafo $G=(V,E)$, llamamos a un emparejamiento máximo a aquel que contiene la mayor cantidad de aristas posible. El valor del emparejamiento máximo es el número de aristas que contiene.

**Ejemplo**

En la figura hay tres ejemplos de emparejamientos máximos. El valor del emparejamiento máximo en $(a)$ es $2$, en $(b)$ es $3$ y en $(c)$ es $2$. Observemos que se cumple la condición de no existen aristas en $M$ que sean adyacentes y cada nodo es adyacente a lo más a una aristas de $M$.

#### Grafo bipartito
Dado un grafo $G=(V,E)$, decimos que $G$ es un grafo bipartito si $V$ es la unión de dos conjuntos disjuntos $L$ y $R$ de nodos, y cada arista en $E$ es adyacente a un nodo $l \in L$ y a un nodo $r \in R$.

### Problema
Deseamos hallar el máximo emparejamiento en un grafo bipartito (también conocido máximo emparejamiento biparito).

**Ejemplo**

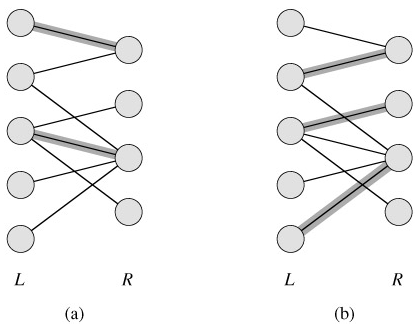
$(a)$ y $(b)$ muestran un emparejamiento bipartito distinto para el mismo grafo, sin embargo, el emparejamiento en $(b)$ es el máximo que se puede lograr, por lo tanto, el valor del máximo emparejamiento bipartito para este grafo es $3$.

### Solución
Utilizando el Lema de Berge, podemos hallar el máximo emparejamiento bipartito con una red de flujo con $|V|+2$ nodos (los nodos originales de $V$ más los nodos especiales $s$ y $t$), y las siguientes aristas:

- Una arista dirigida de $s$ a $l$ para cada nodo $l \in L$ con capacidad $1$.
- Una arista dirigida de $l$ a $r$ con capacidad $1$ si existe una arista $(l,r)$ en $E$.
- Una arista dirigida de $r$ a $t$ para cada nodo $r \in R$ con capacidad $1$.

El valor del máximo emparejamiento bipartito será igual al flujo máximo en esta red.

**Ejemplo**
Para hallar el flujo máximo en el grafo del ejemplo anterior, debemos obtener el siguiente grafo:

Y al hallar el flujo máximo obtenemos el siguiente resultado:

### Reconstrucción de la respuesta
Las aristas que pertenecen al emparejamiento bipartito, son aquellas que van de un nodo $l \in L$ a un nodo $r \in R$ y que tienen flujo igual a $1$.

**Ejemplo**
Las aristas que pertenecen al máximo emparejamiento bipartito en el grafo de ejemplo están marcadas con verde en la siguiente figura. Observar que el flujo que pasa por estas aristas es igual a $1$.

### Algoritmos
- **Dinic**: Se puede demostrar que el algoritmo de Dinic tiene complejidad $O(|V|\sqrt|V|)$ en grafos bipartitos, por lo que tendrá esta complejidad al resolver el problema de máximo emparejamiento bipartito.
- [Algoritmo de Kuhn](https://cp-algorithms.com/graph/kuhn_maximum_bipartite_matching.html): Este es un algoritmo especifico para el problema del emparejamiento bipartito cuyo código es corto, por lo que se puede aprender fácilmente de memoria. Tiene complejidad $O(|V|^3)$, aunque en promedio corre en $O(|V|^2)$.

### Generalización del máximo emparejamiento bipartito
Queremos resolver la siguiente generalización del problema del máximo emparejamiento bipartito para un grafo $G=(V,E)$: hallar el máximo tamaño que puede tener un multiconjunto $M$ de las aristas de $E$ que cumpla con las siguientes restricciones:

- Cada arista $e_i=(l_i,r_i)$ puede estar a lo más $a_i$ veces en $M$.
- Cada nodo $l \in L$ puede ser adyacente de a lo más $b_l$ aristas en $M$.
- Cada nodo $r \in R$ puede ser adyacente de a lo más $c_r$ aristas en $M$.

La solución es hallar el flujo máximo en una red de flujo con $|V|+2$ nodos (los nodos originales de $V$ más los nodos especiales $s$ y $t$), y las siguientes aristas:

- Una arista dirigida de $l_i$ a $r_i$ con capacidad $a_i$ para cada arista $(l_i,r_i) \in E$.
- Una arista dirigida de $s$ a $l$ para cada nodo $l \in L$ con capacidad $b_l$.
- Una arista dirigida de $r$ a $t$ para cada nodo $r \in R$ con capacidad $c_r$.

### Problemas de practica
- https://practice.geeksforgeeks.org/problems/maximum-bipartite-matching/1
- https://atcoder.jp/contests/arc092/tasks/arc092_a
- https://onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=1033
- https://lightoj.com/problem/factors-and-multiples
- https://onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=4406
- https://codeforces.com/contest/512/problem/C
- https://www.spoj.com/problems/ANGELS/en/
- https://omegaup.com/arena/GPMX2022_repechaje/practice/#problems/Homework

## Cobertura mínima de nodos (minimum vertex cover)

### Definiciones
#### Covertura de nodos
Dado un grafo $G=(V,E)$, una covertura de nodos (vertex cover) de $G$ es un subconjunto $C$ de $V$, donde cada arista en $E$ es adyacente al menos a un nodo en $C$.

#### Cobertura mínima de nodos
Dado un grafo $G=(V,E)$, una covertura mínima de nodos es aquella que contiene la mínima cantidad posible de nodos.

**Ejemplo**

En estos ejemplos podemos observar una cobertura mínima de nodos, la cual está marcada con **rojo**.

### Problema
Dado un grafo **bipartito** $G=(V,E)$, deseamos hallar el cubrimiento mínimo de nodos.

### Solución
El [Teorema de Köning](https://en.wikipedia.org/wiki/K%C5%91nig%27s_theorem_(graph_theory)) nos dice que el tamaño de la cobertura mínima de nodos es igual al máximo emparejamiento en un grafo bipartito, por lo tanto, la solución consiste en hallar el máximo emparejamiento bipartito en el grafo.

### Reconstrucción de la respuesta
La respuesta consiste en marcar los nodos que son alcanzables desde $s$ utilizando caminos residuales (es decir, caminos que pasan por aristas donde el flujo es menor a la capacidad en la red residual que queda después de haber ejecutado un algoritmo de flujo máximo en la red). Los nodos que pertenecen a la cobertura mínima de nodos son:

- Sea $l \in L$, si $l$ **no** es alcanzable desde $s$, entonces pertenece al cubrimiento mínimo de nodos.
- Sea $r \in R$, si $r$ **sí** es alcanzable desde $s$, entonces pertenece al cubrimiento máximo de nodos.

[Demostración](https://en.wikipedia.org/wiki/K%C5%91nig%27s_theorem_(graph_theory)#Proofs).

## Conjunto independiente máximo (maximum independent set)
### Definiciones
#### Conjunto independiente
Dado un grafo $G=(V,E)$, un conjunto independiente es un subconjunto de $V$ donde no existe ningún par de nodos adyacentes.

#### Conjunto independiente máximo
Dado un grafo $G=(V,E)$, el conjunto independiente máximo es aquel que tiene la mayor cantidad de nodos posible.

**Ejemplo**

En estos ejemplos podemos observar un conjunto independiente máximo, el cual está marcado con **blanco**.

### Problema
Dado un grafo **bipartito** $G=(V,E)$, deseamos hallar el conjunto independiente máximo.

### Solución
[Se puede demostrar](https://math.stackexchange.com/questions/1758900/relationship-between-maximal-independent-set-and-minimum-vertex-cover) que si $C$ es un cubrimiento mínimo de nodos, entonces $V \backslash C$ es un conjunto independiente máximo (y esto ocurre en cualquier gráfo, no sólo bipartito), es decir, los nodos que no estén en $C$ forman un conjunto indpendiente máximo. Por lo tanto, el tamaño del conjunto independiente máximo es igual a $|V|$ menos el valor del emparejamiento máximo.

### Reconstrucción de la respuesta
La respuesta consiste en marcar los nodos que son alcanzables desde $s$ utilizando caminos residuales después de ejecutar un algoritmo de flujo máximo. Los nodos que pertenecen al conjunto independiente máximo son:

- Sea $l \in L$, si $l$ **sí** es alcanzable desde $s$, entonces pertenece al cubrimiento mínimo de nodos.
- Sea $r \in R$, si $r$ **no** es alcanzable desde $s$, entonces pertenece al cubrimiento máximo de nodos.

En otras palabras, son los nodos que no estén en el cubrimiento mínimo de nodos visto en la sección anterior.

### Problemas de práctica (cubrimiento mínimo de vertices y conjunto independiente máximo)
- https://www.codechef.com/problems/KMHAMHA
- https://codeforces.com/group/Ohoz9kAFjS/contest/266572/problem/D
- https://codeforces.com/gym/102428/problem/A

## Corte mínimo (minimum cut)
### Definiciones
#### Corte entre dos nodos
Dado un grafo ponderado $G=(V,E)$ y dos nodos especiales $s$ y $t$, un corte entre $s$ y $t$ es un subconjunto $C$ de aristas de $E$, tal que no existe ningún camino de $s$ a $t$ en $G=(V,E \backslash C)$. En otras palabras, un corte consiste en eliminar aristas tal que se eliminen todos los caminos de $s$ a $t$.

#### Corte mínimo entre dos nodos
Dado un grafo ponderado $G=(V,E)$ y dos nodos especiales $s$ y $t$, un corte mínimo $C$ entre $s$ y $t$ es aquel donde la suma de los pesos de las aristas en $C$ es la mínima posible.

**Ejemplo**

En la figura se observa un ejemplo de corte mínimo, donde $s$ (source) está marcado con verte, $t$ (sink) está marcado con rojo, y las aristas que se cruzan con la línea punteada son las que pertenecen al corte mínimo, el cual tiene valor de $9$.

### Problema
Dado un grafo ponderado $G=(V,E)$ y dos nodos especiales $s$ y $t$, hallar el corte mínimo entre $s$ y $t$.

### Solución
El [Teorema Max-flow Min-cut](https://brilliant.org/wiki/max-flow-min-cut-algorithm/#:~:text=The%20max%2Dflow%20min%2Dcut,the%20source%20from%20the%20sink.) establece que el valor del flujo máximo entre $s$ y $t$ es igual al valor del mínimo corte entre $s$ y $t$ en un grafo general, donde la capacidad de las aristas es igual a su peso. Por lo tanto, basta con hallar el flujo máximo entre $s$ y $t$ para hallar el corte mínimo.

### Reconstrucción de la respuesta
La respuesta consiste en marcar los nodos que son alcanzables desde $s$ utilizando caminos residuales después de haber ejecutado un algoritmo de flujo máximo. Las aristas que pertenecen al corte mínimo son:

- Sea $u$ un nodo que **sí** es alcanzable desde $s$ y $v$ un nodo que **no** es alcanzable desde $s$. Si existe una arista de $u$ a $v$, entonces esta arista pertenece al corte mínimo.

### Problemas de práctica
- https://codeforces.com/group/Ohoz9kAFjS/contest/266572/problem/B
- https://www.spoj.com/problems/COCONUTS/
- https://codeforces.com/group/Ohoz9kAFjS/contest/266572/problem/C

## Selección de proyectos (project selection)
### Problema
Tenemos $N$ propuestas de proyectos y $M$ máquinas,. El $i$-ésimo proyecto nos daría una ganacia $a_i$ y comprar la $j$-ésima máquina nos generaría un costo $b_j$. Para completar cada proyecto necesitamos comprar un conjunto de máquinas. Si dos o más proyectos necesitan la misma máquina, se puede compartir entre los diferentes proyectos. ¿Cuál es el mayor beneficio que podemos obtener?

### Problema
Tenemos $N$ propuestas de proyectos y $M$ máquinas,. El $i$-ésimo proyecto nos daría una ganacia $a_i$ y comprar la $j$-ésima máquina nos generaría un costo $b_j$. Para completar cada proyecto necesitamos comprar un conjunto de máquinas. Si dos o más proyectos necesitan la misma máquina, se puede compartir entre los diferentes proyectos. ¿Cuál es el mayor beneficio que podemos obtener?

### Solución
La solución consiste en modelar este problema en términos del corte mínimo. Construyamos un grafo bipartito con $N+M+2$ nodos:

- $2$ nodos especiales $s$ y $t$.
- $N$ nodos, uno para cada proyecto, númerados $p_1, p_2, \dots, p_N$.
- $M$ nodos, uno para cada máquina, númerados $m_1, m_2, \dots, m_M$.

Y dibujemos aristas de la siguiente forma:

- Una arista con peso $a_i$ dirigida de $s$ a $p_i$.
- Una arista con peso $b_i$ dirigida de $m_j$ a $t$.
- Una arista con peso $\infty$ de $p_i$ a $m_i$ si necesitamos comprar la máquina $m_i$ para completar el proyect $p_i$.

Ahora hallemos el mínimo corte de $s$ a $t$, al cual llamaremos $mincut$. El mayor beneficio que podemos obtener es es $\sum_{i=1}^{N}a_i-mincut$. Por el teorema Min-cut Max-flow, este corte mínimo es igual al flujo máximo de $s$ a $t$.

### Reconstrucción de la respuesta
Primero hallemos las aristas que pertenecen al corte mínimo. La respuesta está definida de la siguiente forma:

- Si la arista dirigida de $s$ a $p_i$ **no** está en el corte mínimo, es óptimo completar el proyecto $p_i$.
- Si la arista dirigida de $m_j$ a $t$ **sí** está en el corte mínimo, es necesario comprar la máquina $m_j$.

**Ejemplo**
Supongamos que $N=3$, $M=4$, $A=[10,20,3]$, $B=[5,15,4,7]$, el proyecto $p_1$ depende de $m_1$ y $m_2$; $p_2$ depende de $m_2$ y $m_3$; y $p_3$ depende de $m_2$, $m_3$ y $m_4$. El grafo que debemos construir se muestra a continuación:


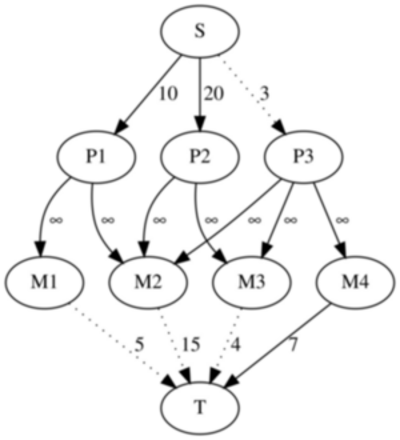
Las aristas que pertenecen al corte mínimo están representadas con líneas punteadas. Podemos observar que el corte mínimo es igual a $27$, por lo que el mayor beneficio que podemos obtener es igual a:

$$
\sum_{i=1}^{3}a_i-mincut=33-27=6
$$

La respuesta es completar los proyectos $p_1$ y $p_2$, y comprar las máquinas $m_1$, $m_2$ y $m_3$.

## Ploblema de la clausura (closure problem)
### Definiciones
#### Clausura en teoría de grafos
Dado un grafo dirigido $G=(V,E)$, definimos a una clausura $C$ como un subconjunto de $V$, tal que para todas las aristas $(u,v)$ donde $u \in C$, se cumple que $v \in C$. Es decir, todas las aristas que salen de un nodo en $C$ están dirigidas a otro nodo en $C$.

### Problema
Dado un grafo **dirigido y ponderado en los nodos** $G=(V,E)$, hallar la clausura $C$ que máximice el peso de los nodos que pertenecn a $C$.

### Solución
Hay que notar que si un nodo $u$ está en la clausura $C$, entonces todos los nodos $v$, tal que existe un camino de $u$ a $v$, deben estar en $C$. La solución consiste en aprovechar esta propiedad y modelar el problema de la clausura como un problema de selección de proyectos.

Construiremos una red de flujo como en el problema de selección de proyectos, donde los nodos con costo positivo serán los proyectos y los nodos con costo negativo serán las máquinas. Si existe un camino de un nodo $u$ con costo **positivo** a un nodo $v$ con costo **negativo**, entonces diremos que $u$ depende de $v$ y pondremos una arista de $u$ a $v$ en la red de flujos.

La respuesta será el máximo flujo en esta red.

### Reconstrucción de la respuesta
La respuesta se reconstruye igual que en el problema de [selección de proyectos](https://hackmd.io/vBg6kDFbScWM-890kqWYew?both#Reconstrucci%C3%B3n-de-la-respuesta4).

## Flujos con demanda (flow with demands)

## Flujo máximo con costo mínimo (max-flow min-cost)

## Flujo con costo mínimo (min-cost flow)

## Técnicas adicionales
### Capacidad y demanda en nodos
### Descomposición en caminos de flujo unitario