> 本文章是4Seas社区的以太坊技术学习文字稿,了解我们更多活动与分享,[可从此处查询](https://app.sola.day/event/4seas)。
> [分享者: WongSSH Twitter](https://x.com/wong_ssh)
> [4Seas 社区 Twitter](https://x.com/4seasDeSoc)
## 概述
作为一名资深智能合约工程师,我认为以太坊在应用领域是“浅”的,即开发者很容易通过学习底层知识的方法掌握以太坊。相比于目前存在的其他教程,本文强调自底向上的通过实践的方式学习以太坊开发,我们会从以太坊交易构建、EVM 的运行原理开始介绍,逐步向上学习。虽然本教程强调自底向上,但是我们仍会屏蔽一部分较为复杂且对应用开发并没有直接作用的知识,比如以太坊内存池的交易规则等。另外,我们也会屏蔽一些关于密码学底层的内容,这部分内容可能会在未来的教程内逐步引入。
## 前置准备
由于本文强调通过实践入门以太坊开发,所以任何准备学习本教程的用户都需要安装以下应用。如果没有特殊说明,本文内所有内容都可以在 Unix-like 操作系统流畅完成,对于 Windows 系统用户,可以尝试使用 WSL 完成本文内的实践任务。
首先是以太坊开发必备的 [Foundry](https://getfoundry.sh/) 框架。Foundry 框架一站式提供了智能合约开发和测试、以太坊交互和本地测试网功能,对于智能合约工程师而言,只需要 Foundry 就可以完成所有工作。
其次是 JavaScript 的执行系统,假如读者本机内存在 `node.js` 等,可以直接使用。假如读者本地不存在任何 JavaScript 运行时,那么我建议读者在本机内安装 [bun](https://bun.sh/)。这是一个高效现代的 JavaScript 执行环境。
最后,读者可以安装 VSCode 等代码编辑器。对于 Solidity 支持,目前 VSCode 是体验最好的代码编辑器。当然,理论上读者可以安装任何代码编辑器,比如 [Zed](https://zed.dev/) 等。
## 助记词与私钥
初入加密货币,相信所有人都在各种钱包初始化时设置并记录过自己的助记词。助记词有 12 / 15 / 18 / 21 / 24 等多个版本,我们可以使用 Foundry 内的 `cast` 指令快速生成特定长度的助记词,比如可以使用以下命令生成 12 word 的助记词:
```bash
cast wallet nm -w 12
```
读者一定好奇助记词的底层原理是什么?Learn me a bitcoin 内的 [Mnemonic Seed](https://learnmeabitcoin.com/technical/keys/hd-wallets/mnemonic-seed/) 一节图文并茂的展示了助记词的生成原理和过程。简单来说,助记词是根据不同长度的熵生成的,比如 128 bit 长度的熵值可以生成 12 words 长度的助记词。每一个 words 代表 11 bit 长度的熵值,此处读者一定好奇 12 words 的助记词应该对应 132 bit 的熵值,多出的 4bit 是从何而来?多出的 4 bit 实际上是 checksum。我们会将输入的熵值进行 SHA256 算法,然后取结果的前 4 bit 作为 checksum 放到最终输出的助记词内部。
Foundry 的 cast 指令也允许我们直接使用熵值生成助记词,比如我们可以输入 128 bit 的熵值获得一个 12 words 的助记词:
```
cast wallet nm -e $(head -c 16 /dev/random | xxd -p)
```
此处的 `head -c 16 /dev/random | xxd -p` 的作用是在 `/dev/random` 内读取 16 bytes 长的随机值,而 `xxd -p` 是将读取的随机值转化为 16 进制字符串方便 `cast` 命令读取。`/dev/random` 是操作系统收集外部熵向用户提供随机数的接口,该接口内的随机数来源于键盘敲击等,一般认为是密码学安全的。
可能有朋友认为助记词并不是充分安全,希望在助记词泄漏情况下仍保持一段时间的钱包安全。此时我们就需要引入 Passphrase 概念。如果读者使用过硬件钱包,会发现硬件钱包在显示地址或者签名时需要输入密码,这个密码本质上就是 passphrase。该机制工作原理如下:
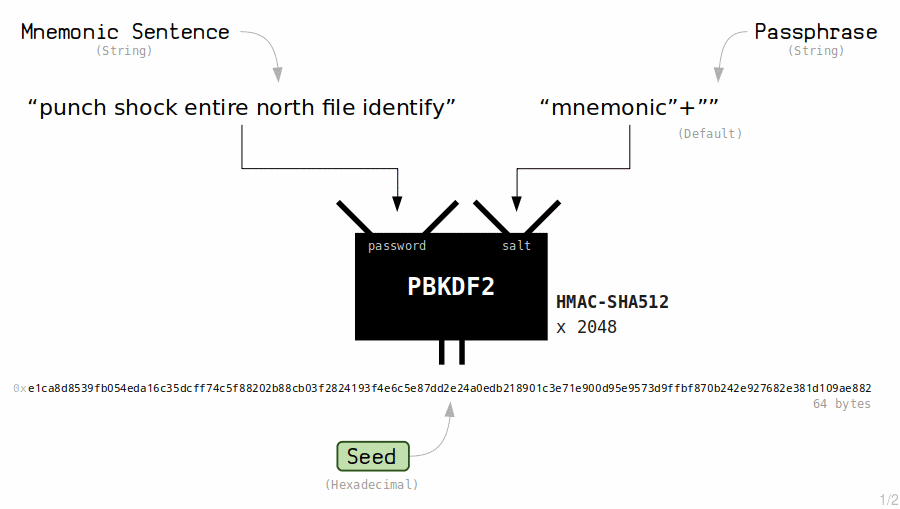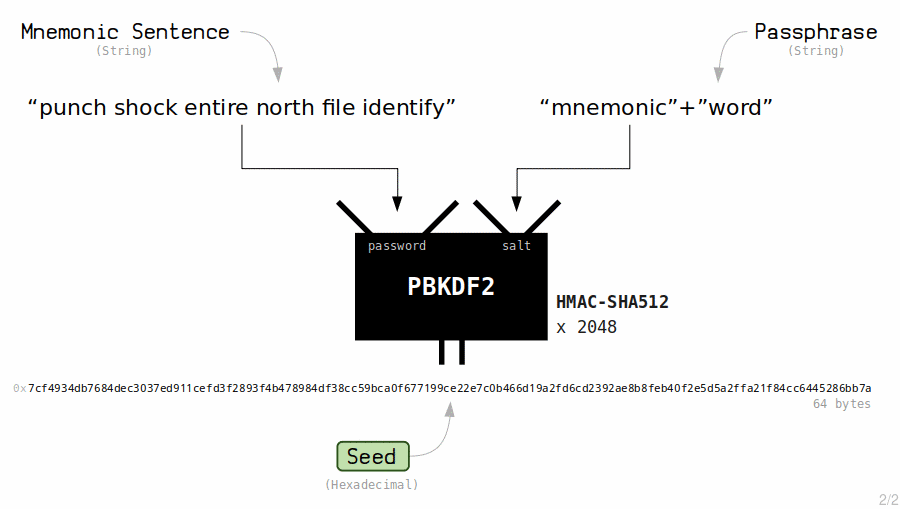
同样,我们可以在 Foundry 内体验一下。Foundry 提供了 Keystore 功能,该功能允许我们导入助记词并用于后续的操作。以下命令中的 `$WORDS` 是我们在环境变量内配置的助记词。此处使用 `passphrase` 是 `password`。在真实场景中,我们应该使用足够复杂的 passphrase。
```bash
cast wallet import --mnemonic $WORDS HDLearn --mnemonic-passphrase password
Enter password:
`HDLearn` keystore was saved successfully. Address: 0x2e848806b493b260724388f57a7c6411f870fe6f
```
Foundry 自动帮我们拍生了一个地址 `0x2e848806b493b260724388f57a7c6411f870fe6f`。关于地址派生的原理,我们会在后续内容中马上介绍。同样的,我们可以尝试不带有 `--mnemonic-passphrase` 进行钱包导入:
```bash
cast wallet import --mnemonic $WORDS HDLearnWithoutPass
Enter password:
`HDLearnWithoutPass` keystore was saved successfully. Address: 0x972b3e75825508bb4b18ef97f109b65cc21a5556
```
我们可以看到派生出的地址并不一致,这是因为引入 passphrase 会改变钱包的 seed,换言之,对于同一助记词使用不同的 passphrase 会产生完全不同的钱包。在此处,我们注意到 Foundry 需要我们输入 password。这个 password 并不影响后续基于助记词进行密钥生成,只是用来加密助记词避免助记词明文在硬盘内出现。Foundry 会默认把所有钱包内容记录在 `.foundry/keystores` 文件夹内部,我们可以打开一个 keystore 文件:
```json
{"crypto":{"cipher":"aes-128-ctr","cipherparams":{"iv":"5661ab77f94467dd436b4411358e9270"},"ciphertext":"464a1d890f405241c31a0e1688a54d7d0d6bb9440992c85f162e7a1a0e8aaabe","kdf":"scrypt","kdfparams":{"dklen":32,"n":8192,"p":1,"r":8,"salt":"c182544f0da0d4e7bcf6a6af1c9e83913739bc9365b35ae8e2070d050d08686e"},"mac":"cfd78b6d730fc0cabc306a1c95be6e5097377f7d852c1e950cbba8881eeb392c"},"id":"012f1dba-dddb-4ed1-a854-34e94c1aef9d","version":3}
```
上述文件内大部分标识都与密码学算法有关,简单来说,我们使用了 `aes-128-ctr` 算法加密**私钥**对应的熵值(注意,虽然上文我们在导入时给定了 `mnemonic`,但 keystore 内部并不会保存助记词,而只是保存助记词派生出的私钥)。在硬件钱包中也有类似的设计,大家使用硬件钱包时需要输入一个密码用来解锁内部的存储的熵值,然后在调用具体钱包时,再次需要输入 passphrase 进一步确定派生私钥的熵值。
> 假如读者现在就希望了解上述内容中的 `ase-128-ctr` 以及 `PBKDF2` 的具体内容,可以阅读 [David Wong](https://x.com/cryptodavidw) 老师出版的 《深入浅出密码学》
当我们了解到助记词生成后,我们将学习另一个复杂的概念——HD 钱包。HD 钱包引入了派生路径等内容,允许我们使用单个助记词生成数量庞大的私钥。我们可以使用 `cast` 命令派生一个私钥:
```bash
cast wallet private-key --mnemonic $WORDS --mnemonic-derivation-path "m/44'/60'/0'/0/0"
```
这实际上就是在上文中,我们导入 `HDLearn` 时显示的地址对应的私钥。使用派生路径进行密钥派生是一个稍微复杂的密码学过程,核心是使用一系列密钥派生算法基于我们最初输入的 seed 派生出一系列密码学上安全的密钥。
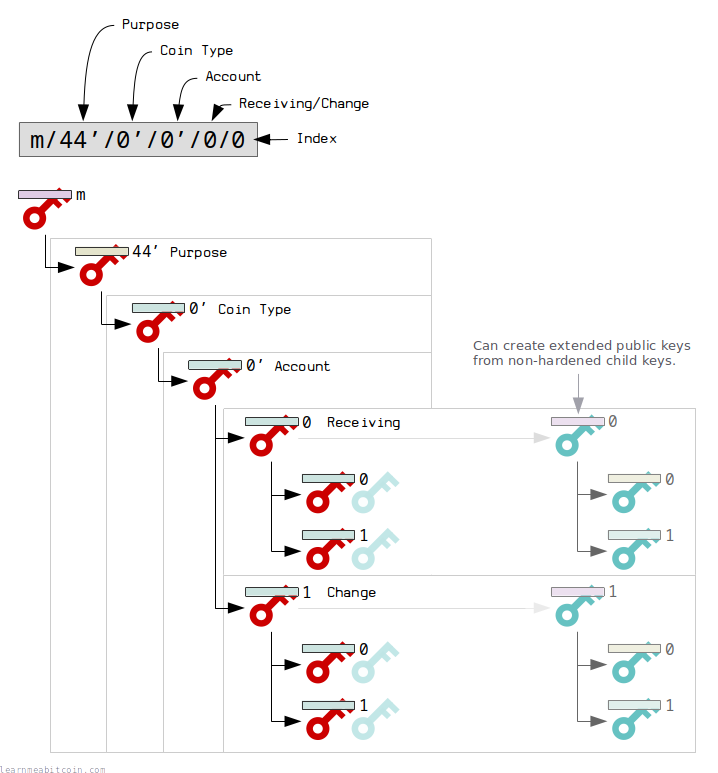
上图显示了 BTC 派生路径规则,而以太坊没有使用如此复杂的派生规则,一般我们只会使用 `m / Purpose / Coin Type / Account` 部分。`CoinType` 部分存在 [SLIP-0044](https://github.com/satoshilabs/slips/blob/master/slip-0044.md) 进行规范。
## 公钥与地址
在上一节中,我们介绍 BIP39 规范的助记词标准和 BIP42 规范的私钥派生标准。在本节中,我们将进一步介绍在非对称密码系统内与私钥对应的公钥以及以太坊如何从公钥内派生地址。
可能很多开发者认为密码学是困难的,但是 Bitcoin 和 Ethereum 使用的椭圆密码学实际上在实现上并不复杂。在我之前编写的 [椭圆曲线密码学与 Typescript 实现](https://blog.wssh.dev/posts/secp256k1-ts/) 一文中就已经对椭圆密码学实现进行详细介绍。具体来说,Bitcoin 和 Ethereum 都使用了 secp256k1 曲线,但是需要注意 Bitcoin 在 Taproot 升级后引入了 schnorr 签名。当然,本质上 schnorr 签名也是椭圆曲线,这是使用的数学基础并不一致。
> 为什么选择 secp256k1 曲线而不是其他椭圆曲线?原因是 secp256k1 的参数选择是 [非随机](https://bitcointalk.org/index.php?topic=289795.msg3183975#msg3183975) 的,并且不是由 NIST 确定的,所以虽然 secp256k1 曲线性能稍差,但是安全性理论上比较高。schnorr 签名没有被早期 Bitcoin 使用是因为 2010 年该签名算法才不受专利保护
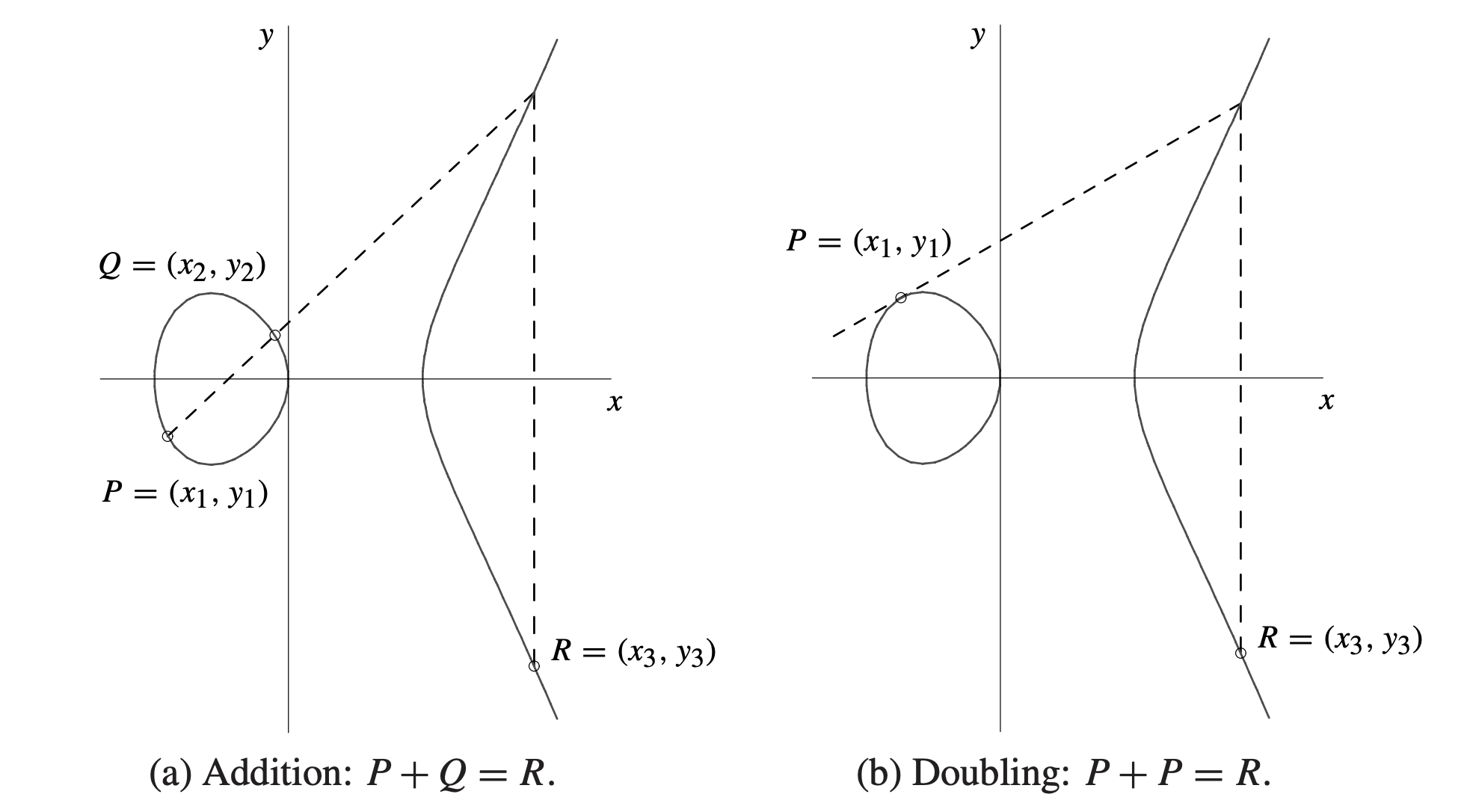
我们首先研究 secp256k1 内如何获得通过私钥计算获得公钥,此处我们只需要进行如下计算:
$$
Q = dG
$$
其中 $Q$ 代表公钥,而 $d$ 代表私钥,而 $G$ 是一个常数。在椭圆曲线中,进行正向进行上述乘法计算很快速,但是不可能通过 $Q$ 分解出私钥。当然,对于量子计算机而言,存在 Shor's algorithm 方法进行有效分解,所以以 secp256k1 为代表的椭圆曲线是非量子安全的。
接下来,我们将进行代码演示。首先我们需要创建任意 Typescript 项目并安装 `viem` 依赖,但是本节课程中,我们并不会直接使用 `viem` 与以太坊进行交互,因为这个库对我们而言太高级了,大部分时间我们都会使用 [noble-curves](https://github.com/paulmillr/noble-curves) 进行密码学教学以及使用 [ox](https://oxlib.sh/) 进行数据编码和解码。我们先给出一个规范的使用 `noble-curves` 标准方法的使用私钥计算公钥的代码:
```typescript
import { secp256k1 } from "@noble/curves/secp256k1";
const PRIVATE_KEY =
"...";
const compressPubKey = secp256k1.getPublicKey(PRIVATE_KEY);
const fullPubKey = secp256k1.getPublicKey(PRIVATE_KEY, false);
console.log(`Compressed PubKey: ${compressPubKey.toHex()}`);
console.log(`Not Compressed PubKey: ${fullPubKey.toHex()}`);
```
输出如下:
```bash
Compressed PubKey: 03a9fdc6724af01e52280d32965eae6d35daf339c6f08a0fd5e93540addb6e8c69
Not Compressed PubKey: 04a9fdc6724af01e52280d32965eae6d35daf339c6f08a0fd5e93540addb6e8c6957fb89d5dac7fca086430d5ca2430010a6f6e93c3ccf1b5c6cf8e62d140af9a9
```
上述过程中,我们输出了两种不同格式的公钥,第一种被称为压缩公钥(Compressed public key),压缩公钥使用 `02` 或 `03` 开头,只使用公钥的 `x` 坐标进行编码。`02` 或 `03` 代表对应的 `y` 值不同,从上图中,我们可以看到同一个 `x` 有可能对应 2 个 `y`,此时我们就需要通过 `02` 或 `03` 指定我们的公钥到底对应哪一个 `y` 值。
而非压缩公钥(uncompressed public key) 就是简单很多,这种格式使用 `04` 开头,剩下的内容第一部分存储 x 坐标,第二部分用于存储 y 坐标。这种编码格式也是 Bitcoin 内部最常用的编码规则,具体可以参考 [Public Key](https://learnmeabitcoin.com/technical/keys/public-key/) 文章。在以太坊内部,我们一般直接使用非压缩公钥,同时也不会增加 `04` 前缀。
接下来,我们将展示公钥计算的底层原理,代码如下:
```typescript
const { ProjectivePoint } = secp256k1;
console.log(
ProjectivePoint.BASE.multiply(
PRIVATE_KEY
).toAffine(),
);
```
此处的 `ProjectivePoint.BASE` 就是 Project 下的 `G` 坐标。Projective 是一种数学变化,在 Projective 下进行的椭圆曲线计算速度会大幅度快于在 x-y 坐标系内进行的计算。我们可以使用 `toAffine` 函数将 Projective 下计算的结果转化为 x-y 坐标系结果。上述代码输出如下:
```json
{
x: 76889253345063424038037441488889217732411355661863396587729873438930254072937n,
y: 39795647744762050057017484826977589713767566384616292013490163034194686179753n,
}
```
简单验证就可以知道 `x` 的16进制格式为 `0xa9fdc6724af01e52280d32965eae6d35daf339c6f08a0fd5e93540addb6e8c69`,其实与上文使用 `getPublicKey` 获得的结果是一致的。当然,`cast` 命令也提供了更加快速的获取公钥的方法,命令如下:
```bash
cast wallet public-key --account HDLearn --mnemonic-derivation-path "m/44'/60'/1'"
```
输出结果如下:
```
0xa9fdc6724af01e52280d32965eae6d35daf339c6f08a0fd5e93540addb6e8c6957fb89d5dac7fca086430d5ca2430010a6f6e93c3ccf1b5c6cf8e62d140af9a9
```
实际上就是未压缩且不包含 `0x04` 前缀的格式。既然介绍了公钥计算,那么我们也可以简单介绍 secp256k1 内的签名计算,过程如下:
我们首先介绍一下椭圆曲线密码学签名和验证的基础原理。签名流程如下:
1. 使用随机数生成器获得一个位于 $k \in [1,N−1]$。此处的 $N$ 为一个常数
2. 计算 $kG = (x_1, y_1)$,并计算 $r = x_1 \mod N$
3. 计算 $s = k^{-1}(m + dr) \mod N$。此处的 $m$ 指需要签名的数据(一般是一个哈希值),而 $d$ 代表用户的私钥
此时,用户可以对外给出 $r$ 和 $s$ 作为自己的签名。当然,此时签名验证者也知道用户的公钥 $Q$。那么验证者如何验证用户正确使用了私钥进行签名呢?我们可以做如下推导:
$$
s = k^{-1}(m + dr) \mod N \Leftrightarrow k = s^{-1}(m + dr) \mod N
$$
上述推导实际上就是两侧同时乘以 $k$ 然后除以 $s$ 即可。
有了上述推导后,我们可以继续如下计算:
$$
\begin{align}
k &= s^{-1}(m + dr) = s^{-1}m + s^{-1}dr \\
&\Leftrightarrow kG = s^{-1}mG + s^{-1}rdG = s^{-1}mG + s^{-1}rQ
\end{align}
$$
在以太坊中,我们的给出的签名 `r / s / v`。此处的 `r` 指的是 $kG$ 的 x 坐标,而 $s$ 就是上文介绍的用户使用私钥计算的结果,而 `v` 是为了处理潜在可能存在两个 $kG$ 的情况(即上文介绍的 1 个 x 值在图上对应 2 个合法 y 值)。显然,我们的私钥将可以通过以下公式计算获得:
$$
d = r^{-1}(ks - m) \mod N
$$
此处的 $k$ 是保密的,所以正常情况下上述计算难以进行。但是假如我们在不小心两次签名使用了同一个 $k$,那么我们可以通过以下公式推导 $k$ 值
$$
k = (s_1 - s_2)^{-1}(m_1 - m_2) \mod N
$$
所以一般来说,$k$ 都有一套严格的推导方法。限于篇幅,我们就不在此处详细介绍。此处需要介绍另一个有趣的规则,即 `lowS` 规则。实际上 `s` 和 `N-s` 都可以通过以上述 secp256k1 的签名验证算法,为了避免交易延展性问题,我们引入了 `lowS` 规则,即所有签名的 `s` 都应小于 `N / 2`。交易延展性是一个常在 Bitcoin 技术领域内讨论的话题,该话题指用户发出的交易是否可以被节点篡改。在没有 `lowS` 规则前,理论上节点可以将用户交易中的 `s` 替换为 `N-s`。对于用户而言,交易内容没有改变,但是交易的 TXID 发生了变化,这会导致很多麻烦。
在此处,我们可以继续利用 `noble` 提供的密码学函数进行签名操作:
```typescript
import { secp256k1 } from "@noble/curves/secp256k1";
import { keccak_256 } from "@noble/hashes/sha3";
const PRIVATE_KEY = BigInt(
"...",
);
const MSG_HASH = keccak_256.create().update("test").digest();
const signature = secp256k1.sign(MSG_HASH, PRIVATE_KEY);
console.log(signature);
```
输出如下:
```json
Signature {
r: 109697458591367185375541540542336406209044478109552519427741268933681375216984n,
s: 43012429767922800270278685707994419241638160082146399923099743210869443406786n,
recovery: 1,
...
```
在此处,我们不会演示如何直接使用底层密码学原语进行签名操作,因为 $k$ 值的选择稍微复杂,需要参考 [rfc6979](https://datatracker.ietf.org/doc/html/rfc6979) 标准。但此处我们可以简单给出 `noble-curves` 的签名时的部分代码:
```typescript
// RFC 6979 Section 3.2, step 3: k = bits2int(T)
const k = bits2int(kBytes); // Cannot use fields methods, since it is group element
if (!isWithinCurveOrder(k)) return; // Important: all mod() calls here must be done over N
const ik = invN(k); // k^-1 mod n
const q = Point.BASE.multiply(k).toAffine(); // q = Gk
const r = modN(q.x); // r = q.x mod n
if (r === _0n) return;
// Can use scalar blinding b^-1(bm + bdr) where b ∈ [1,q−1] according to
// https://tches.iacr.org/index.php/TCHES/article/view/7337/6509. We've decided against it:
// a) dependency on CSPRNG b) 15% slowdown c) doesn't really help since bigints are not CT
const s = modN(ik * modN(m + r * d)); // Not using blinding here
if (s === _0n) return;
let recovery = (q.x === r ? 0 : 2) | Number(q.y & _1n); // recovery bit (2 or 3, when q.x > n)
let normS = s;
if (lowS && isBiggerThanHalfOrder(s)) {
normS = normalizeS(s); // if lowS was passed, ensure s is always
recovery ^= 1; // // in the bottom half of N
}
return new Signature(r, normS, recovery) as RecoveredSignature; // use normS, not s
```
与上文的签名计算公式对比,大家可以发现是完全一致的。
对于签名验证,以太坊执行层使用的策略是首先恢复公钥,即预先假设用户输入的签名是正确的,然后利用上述公式计算出用户的公钥,然后进一步计算出地址,判断用户签名对应的地址与交易的发起地址(`from`) 是否一致。在 go-etherum 对应的代码如下:
```go
func (s EIP155Signer) Sender(tx *Transaction) (common.Address, error) {
if tx.Type() != LegacyTxType {
return common.Address{}, ErrTxTypeNotSupported
}
if !tx.Protected() {
return HomesteadSigner{}.Sender(tx)
}
if tx.ChainId().Cmp(s.chainId) != 0 {
return common.Address{}, fmt.Errorf("%w: have %d want %d", ErrInvalidChainId, tx.ChainId(), s.chainId)
}
V, R, S := tx.RawSignatureValues()
V = new(big.Int).Sub(V, s.chainIdMul)
V.Sub(V, big8)
return recoverPlain(s.Hash(tx), R, S, V, true)
}
```
这其实派生了一种特殊的以太坊合约确定性地址部署方法,该方法被称为 [Nick’s Method](https://medium.com/taipei-ethereum-meetup/nick-method-6f3c7c2dabef)。在后续介绍合约部署时,我们会详细介绍,但简单来说该部署交易使用了随机生成的签名。[EIP7002](https://eips.ethereum.org/EIPS/eip-7002#deployment) 等以太坊系统合约都使用类似的方法进行了部署。
我们可以推导一下如下从 `r / s / v` 参数中反推出 `Q` 的数值(在以下推导中,我们将 $kG$ 记为 $R$):
$$
\begin{align}
kG = R &= s^{-1}mG + s^{-1}rQ\\
sR &= mG + rQ\\
sR - mG &= rQ\\
r^{-1}sR - r^{-1}mG &= Q
\end{align}
$$
在 `noble-curves` 内,我们可以看到如下代码:
```typescript
recoverPublicKey(msgHash: Hex): typeof Point.BASE {
const { r, s, recovery: rec } = this;
const h = bits2int_modN(ensureBytes('msgHash', msgHash)); // Truncate hash
if (rec == null || ![0, 1, 2, 3].includes(rec)) throw new Error('recovery id invalid');
const radj = rec === 2 || rec === 3 ? r + CURVE.n : r;
if (radj >= Fp.ORDER) throw new Error('recovery id 2 or 3 invalid');
const prefix = (rec & 1) === 0 ? '02' : '03';
const R = Point.fromHex(prefix + numToSizedHex(radj, Fp.BYTES));
const ir = invN(radj); // r^-1
const u1 = modN(-h * ir); // -hr^-1
const u2 = modN(s * ir); // sr^-1
const Q = Point.BASE.multiplyAndAddUnsafe(R, u1, u2); // (sr^-1)R-(hr^-1)G = -(hr^-1)G + (sr^-1)
if (!Q) throw new Error('point at infinify'); // unsafe is fine: no priv data leaked
Q.assertValidity();
return Q;
}
```
上述代码中的 `ir` 代表 $r^{-1}$,而 `h` 代表 $m$。需要特别注意 `Point.BASE.multiplyAndAddUnsafe` ,该算法一步实现了最终的计算。
关于以太坊如何对交易进行编码哈希获得 $m$ 是下文的核心内容,在本节中,我们只需要解决最后一个问题,我们的地址如何计算出来。我们先使用 `cast` 命令获取一下上文使用的 `m/44'/60'/1'` 的地址:
```bash
cast wallet address --account HDLearn --mnemonic-derivation-path "m/44'/60'/1'"
```
输出结果为 `0x2e848806b493B260724388F57A7c6411f870fe6f`。接下来,我们尝试将上文获得的该账户的公钥进行 keccak256 哈希计算:
```bash
cast keccak256 0xa9fdc6724af01e52280d32965eae6d35daf339c6f08a0fd5e93540addb6e8c6957fb89d5dac7fca086430d5ca2430010a6f6e93c3ccf1b5c6cf8e62d140af9a9
```
输出如下:
```
0x5e9c7392ca4651cb8c8c051f2e848806b493b260724388f57a7c6411f870fe6f
```
肉眼可见,keccak256 的输出结果与 `cast wallet` 返回的钱包地址似乎有很高的相似性。实际上,以太坊地址就是用户公钥哈希值取后 160 bit 的结果。keccak256 是以太坊中最常被使用的哈希算法,该哈希算法输出的结果有 256 bit,但以太坊地址的长度是 160 bit,所以以太坊选择了截断哈希值的做法。
此处我们也引入一个新名词 `EOA`(Externally Owned Account),所以使用上述 secp256k1 私钥控制的账户都属于 EOA 账户,当然,EOA 账户在以太坊底层与合约还有一个不同,我们会在后文介绍 EVM 时涉及。但随着 [EIP7702](https://eips.ethereum.org/EIPS/eip-7702) 的引入,EOA 与智能合约之间的界限逐渐模糊,现在一个 EOA 地址也可以通过 EIP7702 获得智能合约功能,具体的原理在后续课程介绍 DelegateCall 时会涉及到。
## 交易 ABI 编码
关于以太坊交易,有特别多的字段可以介绍。本节将首先交易中和智能合约开发最有关的字段 `data`。`data` 是一个发送给智能合约的二进制数据,当智能合约收到交易后,就会提取交易中的 `data` 然后执行,所以以太坊内的所有智能合约都需要被外界触发执行。在很多偏学术的资料中,我们一般称 EVM 内的智能合约存在状态机的特性,这其实也是在描述假如没有发生交易,智能合约的状态就不会发生改变。当然,交易的发起人可能是 EOA 也可能是智能合约,但最初的交易发起人一定是 EOA。
当节点收到一笔交易后,就会构建一个 EVM 对象执行交易的 `data` 字段。EVM 虚拟机是一种基于栈和内存的虚拟机,其构成如下:
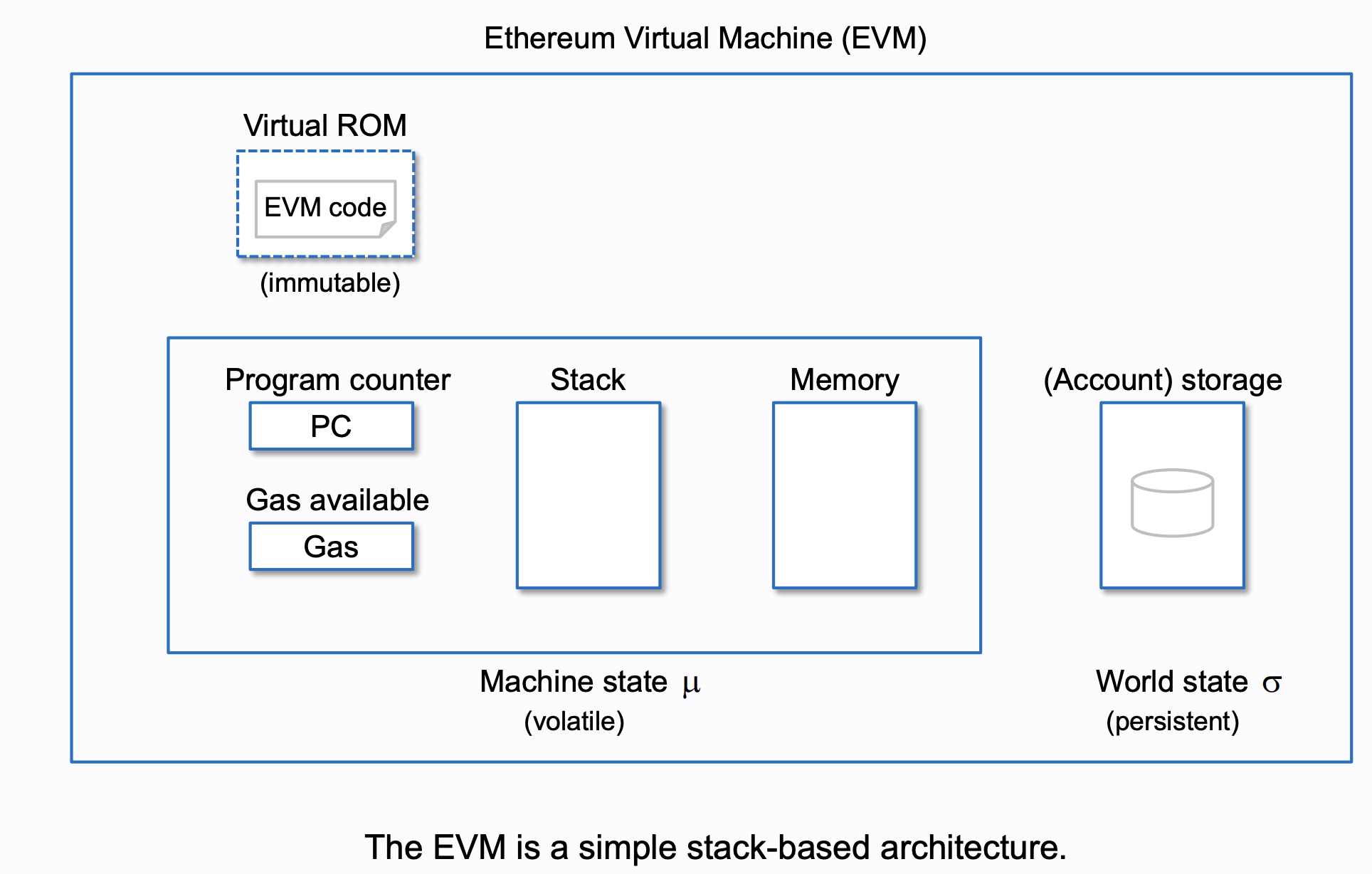
> 上图来自 [ethereum_evm_illustrated](https://takenobu-hs.github.io/downloads/ethereum_evm_illustrated.pdf)。这是一份古老但是目前仍有参考价值的材料,建议读者阅读。当然,上图的缺陷在于忽略了 `calldata` 字段,实际上 `calldata` 也应该被视为 EVM Machine State 的一部分。`calldata` 的特殊性在于,该字段是只读的,即我们可以使用 `calldataload` 读取内部,但不可以写入
节点内的 EVM 虚拟机会读取 EVM Code 并逐条执行内部的指令,在正常情况下,每读取一条指令,`PC` 就会自动增加 1,指向下一条指令,这样 EVM 虚拟机就可以逐条执行所有指令。但是也存在 `JUMP` 和 `JUMPI` 指令,这两条指令可以直接修改 `PC` 数值,将程序跳转到指定位置执行。
在本节课程中,我们可以先对栈进行一个简单介绍。栈可以用来存储待操作数并执行操作,栈最常见的几种操作方法是:
1. `PUSH` 将数据推入栈内部
2. `POP` 将数据从栈顶部弹出
3. `DUP` 复制栈内部的数据
4. `SWAP` 用于交换栈内的数据
接下来,我们可以编写一个简单的程序,计算 `42 + 69` 的结果:
```
PUSH1 42
PUSH1 69
ADD
```
然后,我们可以挑战计算斐波那契数列的 EVM 字节码(警告以下代码不要直接执行,在不限制 gas limit 情况 EVM 执行器会因为无限循环崩溃):
```
PUSH0
PUSH1 0x01
JUMPDEST
DUP1
SWAP2
ADD
PUSH1 0x03
JUMP
```
在上述代码中,我们使用 `JUMP` 进行了无条件跳转,跳转目的地是 `PUSH1 0x03` 推入的 `0x03` 位置。在 EVM 中,所有的跳转目的地都需要使用 `JUMPDEST` 进行标识。警告,上述字节码在执行时会不断循环消耗资源。我们肯定不希望代码是死循环的,所以我们可以使用 `JUMPI` 指令进行条件判断跳转。比如以下代码给出了计算第一个大于 `0xff` 的斐波那契数的方法:
```
PUSH0
PUSH1 0x01
JUMPDEST
DUP1
SWAP2
ADD
DUP1
PUSH1 0xff
GT
PUSH1 0x03
JUMPI
```
从此处,我们可以初探 EVM 内代码运行的基础原理。实际上,在 Solidity 的入口,会存在专门的函数派发器。这是因为单个合约内往往存在多个功能可以被外界调用,我们需要根据用户调用来跳转到合适位置执行代码。函数派发器的伪代码如下:
```typescript
switch (selector) {
case "transfer": jump transfer code start
case "approve": jump approve code start
}
```
假如我们在函数派发器内使用字符串进行匹配显然是低效的,Solidity 工程师引入了函数选择器(selector) 作为派发的依据。举例说明,比如一笔简单的 USDC 转账交易的 `data` 是以下形式:
```
0xa9059cbb000000000000000000000000d8da6bf26964af9d7eed9e03e53415d37aa96045000000000000000000000000000000000000000000000000000000003b9aca00
```
此处 `0xa9059cbb` 就是函数选择器,用于 solidity 识别该代码调用了合约的那个具体函数。那么我们该如何计算一个函数的函数选择器?首先,我们需要知道函数的定义,比如 ERC20 的 `transfer` 函数定义如下:
```solidity
function transfer(address to, uint256 amount) external returns (bool);
```
上述定义中的 `address` / `uint256` / `bool` 都代表变量类型,而 `to` / `amount` 都是变量名称,其他的 `function` 等都是 solidity 的关键词,我们会在后续介绍具体开发时逐步介绍。有了上述函数定义后,我们可以将其简写为:
```
transfer(address, uint256)(bool)
```
简写只包含函数名称以及必要的类型,上述简写还包含了返回值的类型。此时,我们就可以使用 `cast` 命令计算函数选择器:
```bash
cast sig "transfer(address, uint256)(bool)"
```
上述命令输出为 `0xa9059cbb`,我们可以将其视为一个数字,这意味着我们可以在编写派发器时使用二分查找以实现低时间复杂度的搜索。当然,Vyper 的开发者 [Charles](https://x.com/big_tech_sux) 在近几个月研究出来比二分查找更快的派发算法,具体可以参考 [Sparse, Constant Time Jump Tables](https://blog.vyperlang.org/posts/selector-tables/) 一文。
实际上,我们也可以使用上述 `"transfer(address, uint256)(bool)"` 生成交易的 calldata,命令如下:
```bash
cast calldata "transfer(address to, uint256 amount)" 0xd8dA6BF26964aF9D7eEd9e03E53415D37aA96045 1000000000
```
在这里,我们可以提前给出调用链上函数的方法:
```bash
cast call 0xA0b86991c6218b36c1d19D4a2e9Eb0cE3606eB48 "balanceOf(address)(uint256)" 0xd8dA6BF26964aF9D7eEd9e03E53415D37aA96045 --rpc-url https://eth.drpc.org
```
上述命令的 `call` 代表发起模拟交易,在后续课程中,我们将看到 `call` 在 debug 的巨大作用。`balanceOf(address)(uint256)` 是以下函数定义的缩写:
```solidity
function balanceOf(address account) external view returns (uint256);
```
而 `--rpc-url` 给定了一个可以用来进行请求的以太坊节点。节点收到我们的 `call` 调用后会帮助我们模拟执行交易。注意所有使用 `call` 的交易都不会真实上链,但节点执行该笔交易并将结果返回给调用者。限于篇幅,我们无法在本节详细介绍 `call` 背后的调用 RPC 等情况,这些内容会在下一次课程内被介绍。
继续回到函数选择器计算过程,读者可能还是希望知道底层原理,我们可以调用以下命令:
```bash
cast keccak256 "transfer(address,uint256)"
```
输出为 `0xa9059cbb2ab09eb219583f4a59a5d0623ade346d962bcd4e46b11da047c9049b`。截断该输出的前 4 bytes,你可以得到 `0xa9059cbb` 的结果。这就是函数选择器的底层原理,本质上就是拿标准化的函数定义进行 keccak256 哈希获得。
在很多时候,特别是对于一些特殊的逆向任务,我们都是拿到的原始的选择器,如 `0x095ea7b3`,我们希望知道对应的函数定义,此时我们就需要借助数据库的力量。开发者常用的数据库是:
1. [openchain](https://openchain.xyz/signatures)
2. [4byte.directory](https://www.4byte.directory/)
当然,更常用的方法是直接调用 `cast 4b 0x095ea7b3` 命令等待返回值。还有一些情况,比如我们获得了完整的源代码,但我们希望直接提取合约内的所有函数选择器,此时可以使用 Foundry 开发包内的 `forge` 命令,比如对 Uniswap v4 库,我们可以使用如下命令:
```bash
forge inspect src/PoolManager.sol methods
```
输出如下(限于篇幅存在部分截断):
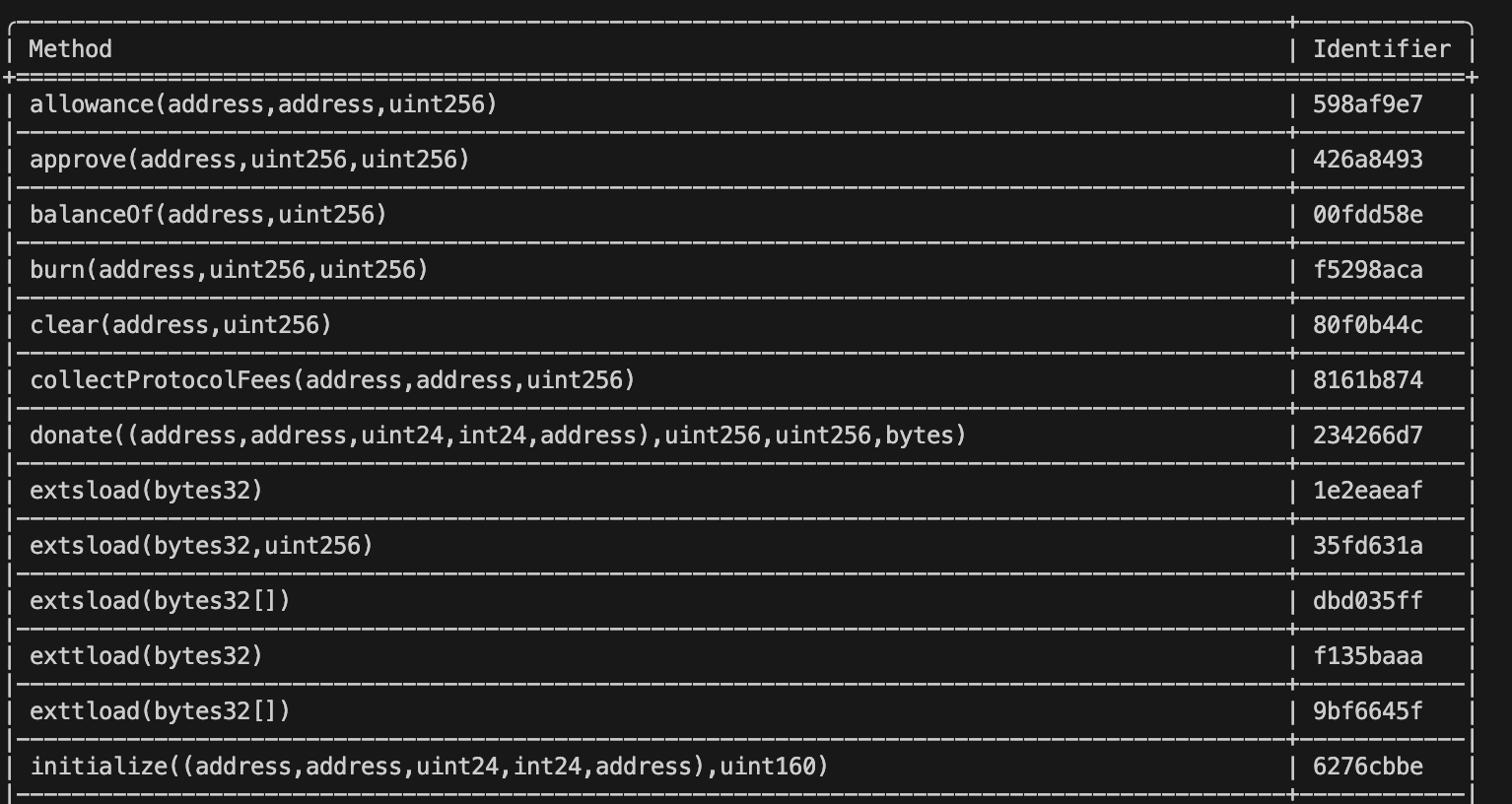
此处我们可以看到一些有趣的函数名,比如:
```
exttload(bytes32[])
```
在 solidity 中,我们允许用户传入一组数据,所有基础类型都存在对应的 Array 版本,比如 `uint256[]` 等。在稍后内容中,我们会介绍 solidity 如何对 `uint256[]` 或 `bytes32[]` 等类型进行编码。
另外,我们还可以看到 `initialize((address,address,uint24,int24,address),uint160)`,该函数名对应的 solidity 内的函数定义如下:
```solidity
struct PoolKey {
/// @notice The lower currency of the pool, sorted numerically
address currency0;
/// @notice The higher currency of the pool, sorted numerically
address currency1;
/// @notice The pool LP fee, capped at 1_000_000. If the highest bit is 1, the pool has a dynamic fee and must be exactly equal to 0x800000
uint24 fee;
/// @notice Ticks that involve positions must be a multiple of tick spacing
int24 tickSpacing;
/// @notice The hooks of the pool
address hooks;
}
function initialize(PoolKey memory key, uint160 sqrtPriceX96) external returns (int24 tick);
```
而 `(address,address,uint24,int24,address)` 是结构体 `PoolKey` 的表示,也是将结构体的构成元素的类型抽取出来。
在使用 `cast` 命令时,我们会使用如下命令表示 `uint256[]` 为代表的 array 类型:
```bash
cast calldata "array(uint256[])" "[1,2,3]"
```
而结构体则使用如下方法表示:
```
cast calldata "struct((uint256, uint256),uint256[])" "(0xff, 0xfff)" "[1,2,3]"
```
在本节的最后,我们介绍 calldata 是如何被编码的(在后文,我们称 calldata 编码为 ABI 编码,“ABI 编码”这一称呼更加通用),这对于我们逆向常规 solidity 程序以及 debug 是有帮助的。目前 solidity 和 vyper 都使用了 solidity 规范的编码方式。以太坊共识层最常被使用 SSZ 编码从原理上与 ABI 编码有很多同构的地方,假如读者有兴趣,可以阅读我之前编写的 [深入探索以太坊共识层:存款与提款](https://blog.wssh.dev/posts/eth2-deposit-withdraw/) 一文。
第一,我们需要知道 ABI 编码内分为静态类型与动态类型两类:
1. 静态类型,指 `uint256` / `uint128` / `bytes32` / `bool` 类型等固定长度的类型,这些类型统统会在 ABI 内被编码为 256 bit 长度。所以即使只使用 1 bit 的 `bool` 类型在编码后仍会占用 256 bit 空间
2. 动态类型,指 `bytes` / `string` / `uint256[]` 等类型,这些类型编码较为复杂
对于只包含静态类型函数的 calldata 生成,我们的工作非常简单,比如 `transfer(address to, uint256 amount)`,参数 `to` 为 `0xd8dA6BF26964aF9D7eEd9e03E53415D37aA96045` 而 `amount` 数值为 `1000000000`,函数选择器为 `0xa9059cbb`我们可以如此操作:
```
0xa9059cbb
000000000000000000000000d8da6bf26964af9d7eed9e03e53415d37aa96045
000000000000000000000000000000000000000000000000000000003b9aca00
```
将上述三行拼接在一起就可以获得最终的 calldata 编码。需要说明的是,我们可以使用 `cast to-uint256 1000000000` 获得某一个数值在 `uint256` 下的表示。当然,一般我们都是获得 calldata 逆向其可能存在的内容,此时我们可以使用 `cast` 指令输出类似的结果,如:
```bash
cast pretty-calldata 0xa9059cbb000000000000000000000000d8da6bf26964af9d7eed9e03e53415d37aa96045000000000000000000000000000000000000000000000000000000003b9aca00
```
输出如下:
```bash
Possible methods:
- transfer(address,uint256)
------------
[000]: 000000000000000000000000d8da6bf26964af9d7eed9e03e53415d37aa96045
[020]: 000000000000000000000000000000000000000000000000000000003b9aca00
```
对于动态类型而言,编码稍有复杂。以 `cast calldata "array(uint256, uint256[])" 0xfffff "[1,2,3]"` 为例,我们直接将其结果进行 `pretty-calldata`。以下命令中的 `--offline` 是指示 `cast` 不需要通过互联网搜索函数选择器对应的函数名
```bash
cast calldata "array(uint256 t1, uint256[] t2, uint256 t3)" 0xdead "[1,2,3]" 0xbeef | cast pretty-calldata --offline
```
输出如下:
```
Method: 46fe4ca9
------------
[000]: 000000000000000000000000000000000000000000000000000000000000dead
[020]: 0000000000000000000000000000000000000000000000000000000000000060
[040]: 000000000000000000000000000000000000000000000000000000000000beef
[060]: 0000000000000000000000000000000000000000000000000000000000000003
[080]: 0000000000000000000000000000000000000000000000000000000000000001
[0a0]: 0000000000000000000000000000000000000000000000000000000000000002
[0c0]: 0000000000000000000000000000000000000000000000000000000000000003
```
首先 `000` 部分是就是 `t1` 对应的数值,而 `040` 部分内的数值显然是 `t3` 对应的数值,而且 `080 - 0c0` 部分应该是 `[1, 2, 3]` 的数值部分,而 `060` 部分的 3 刚好是 `t2` 的长度。而 `020` 部分内部到底是什么?`020` 部分内的数据其实是偏移量(offset),指其具体数据内容(包括长度和数值)在 calldata 内部的位置。比如此处 `t2` 的具体数据内容包括长度 3 和具体的 `1, 2, 3` 三个数据。
简单来说,在进行动态编码时,我们会在动态类型所在位置插入一个传送门指向真实的 calldata 所在的位置,当我们 calldata 解析器读到传送门后,我们就可以跳转到真正的位置上获得长度信息,并按照长度信息读取数据。对于动态类型中的 `bytes` 类型和 `string` 类型(本质上其实就是 `bytes` 类型),我们需要特别注意,
```bash
cast calldata "array(string t)" "Hello, World" | cast pretty-calldata --offline
```
上述案例返回值如下:
```bash
Method: 5a971830
------------
[000]: 0000000000000000000000000000000000000000000000000000000000000020
[020]: 000000000000000000000000000000000000000000000000000000000000000c
[040]: 48656c6c6f2c20576f726c640000000000000000000000000000000000000000
```
首先,我们可以检查一下 `48656c6c6f2c20576f726c64` 到底是什么字符串?使用指令 `cast to-utf8 48656c6c6f2c20576f726c64` 获得输出如下:
```
Hello, World
```
这与我们的预期是一致的。由于 UTF8 编码本身兼容 ascii 编码,所以此处建议使用 `to-utf8` 而不是 `to-ascii`。而 `0x20` 位置的 `c` 则是指 `48656c6c6f2c20576f726c64` 的长度(10 bytes)。
为了完整性,我们在此处介绍我从未在真实业务场景下见过的 `(uint256, uint256[], uint256)[]` 的情况:
```bash
cast calldata "array((uint256, uint256[], uint256)[])" "[(0xff, [1, 2 , 3], 0xee),(0xffff, [4, 5], 0xeeee)]" | cast pretty-calldata --offline
```
输出如下:
```bash
Method: 73815c22
------------
[000]: 0000000000000000000000000000000000000000000000000000000000000020
[020]: 0000000000000000000000000000000000000000000000000000000000000002
[040]: 0000000000000000000000000000000000000000000000000000000000000040
[060]: 0000000000000000000000000000000000000000000000000000000000000120
[080]: 00000000000000000000000000000000000000000000000000000000000000ff
[0a0]: 0000000000000000000000000000000000000000000000000000000000000060
[0c0]: 00000000000000000000000000000000000000000000000000000000000000ee
[0e0]: 0000000000000000000000000000000000000000000000000000000000000003
[100]: 0000000000000000000000000000000000000000000000000000000000000001
[120]: 0000000000000000000000000000000000000000000000000000000000000002
[140]: 0000000000000000000000000000000000000000000000000000000000000003
[160]: 000000000000000000000000000000000000000000000000000000000000ffff
[180]: 0000000000000000000000000000000000000000000000000000000000000060
[1a0]: 000000000000000000000000000000000000000000000000000000000000eeee
[1c0]: 0000000000000000000000000000000000000000000000000000000000000002
[1e0]: 0000000000000000000000000000000000000000000000000000000000000004
[200]: 0000000000000000000000000000000000000000000000000000000000000005
```
假如我们是编码器,第一步我们发现自己需要编码 `T[]` 类型,不管 `T` 是什么,现在原地传入 offset,即在 `000` 位置写入 `0x20` 数据,然后继续分析,发现 `T` 有两个(即包含 `0xff` 和 `0xffff` 两个部分),所以在动态类型编码最开始 `020` 处写入长度 `0x02`。接下来,继续分析发现 `T` 还是一个动态类型,我们需要再次插入 offset,此时我们需要插入相对于当前位置 `0x40` 的偏移值,比如此处的 `0x40` 其实代表 `0x40 + 0x40 = 0x80` 处存在第一个数组 `[1, 2, 3]` 的真实数据,而 `0xe0` 代表 `0x120 + 0x40 = 0x160`。
接下来,我们先完成第一个结构体 `(0xff, [1, 2 , 3], 0xee)` 的编码。对于 `0xff` 而言,美好的静态类型,直接写入即可,对于 `[1, 2, 3]` 而言,这又是一个动态类型,在此处我们写入偏移量,但此处的偏移量依旧是结构体内偏移量,显然,假如需要读取 `[1, 2, 3]`,我们需要从结构体开始的地方跳过 3 个元素,分别是 `0xff` / `[1, 2, 3]` 的长度 / `0xee`,所以此处填入 `0x60`。
我们可以留一个类似但更复杂的交给读者自行处理:
```bash
cast calldata "array((uint256, uint256[], uint256, uint256[])[])" "[(0xff, [1, 2 , 3], 0xee, [0xaa]),(0xffff, [4, 5], 0xeeee, [0xaaaa])]" | cast pretty-calldata --offline
```
## 总结
在本次课程中,我们主要介绍了以下内容:
1. 助记词的随机值的本质以及派生路径
2. 私钥、公钥与地址之间的关系,特别介绍 go-ethereum 如何验证签名
3. 私钥签名的数学原理,需要注意 $k$ 的重要作用
4. EVM 基础的执行流程,目前我们只涉及了栈的有关操作
5. 函数选择器的存在原因和计算方法
6. ABI 编码的具体规则
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet