# Week 5

## Monday

## Tuesday
### Morning: Linear Algebra

- Vector is a combination of numbers to represent features
- Mathematically speaking: a vector v is
$\mathcal{v} \in \mathbb{R}^n$ which is a column vector of number:

$$
\vec{v} = \begin{pmatrix} v_1 \\ v_2 \\ \dots \\ v_n \end{pmatrix}
$$
where n is the number of element in the vector.

- In a dataset, a vector is a particular training instance, which is usually corresponding to a row in the dataset
- Lenght, magnitude, norm of vectors:
$\vec{v} = ||v|| = \sqrt{v_{1}^{2} + v_{2}^{2} + \dots + v_{n}^{2}}$

- Unit vectors (basis):
$\vec{i}$ and $\vec{j}$ are the basis of the vector space in which $\vec{v}$ lies:
$$
\vec{v} = \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}
= v_1.\begin{pmatrix} 1 \\ 0 \end{pmatrix} + v_2.\begin{pmatrix} 0 \\ 1 \end{pmatrix}
= v_1.\hat{i} + v_2.\hat{j}
$$

- Dot products of 2 vectors:
$$
\vec{a}.\vec{b} = \sum_{i}^{n}{a_ib_i} = ||a||.||b||.cos\phi
$$

- Dot product of $\vec{a}$ and $\vec{b}$ is
- **is positive** when they point at 'similar' directions. Bigger = more similar
- **equals 0** when they are perpendicular.
- **is negative** when they are at dissimilar directions. Smaller (more negative) = more dissimilar

- Cosine similarity of 2 vectors: how similar their directions are:

$$
similarity(\vec{a},\vec{b}) = cos\phi = \frac{\sum_{i}^{n}{a_ib_i}}{||a||.||b||}
$$

- Vectors operations and properties:
- Self-dot product: $$||x||^2 = \vec{x}.\vec{x} $$

- Commutative: $\vec{x}.\vec{y} = \vec{y}.\vec{x}$

- Distributive: $\vec{x}.(\vec{y} + \vec{z}) = \vec{x}.\vec{y} + \vec{x}.\vec{z}$

- Associative: $\vec{x}.(a\vec{y}) = a(\vec{x}.\vec{y})$

- Vector projection: $$(\vec{x}.\vec{y})\frac{\vec{y}}{||y||^2}$$

- Hadamard product (Element-wise multiplication): the output is another vector


- Matrix is a combination of vectors, or 2D array of numbers
- Broadcasting when working with matrices of different shapes:

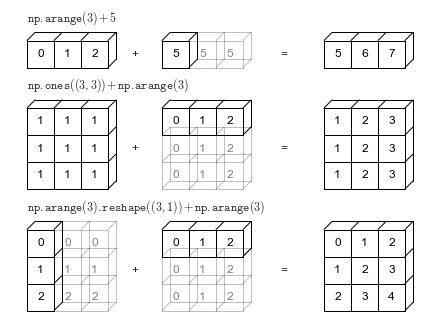
- Matrix multiplication: perform dot product of first matrix's row and second matrix's column:
<div align="left">
<img src="https://raw.githubusercontent.com/madewithml/images/master/basics/03_NumPy/dot.gif" width="450">
</div>

- Linear Regression in a matrix form:

$$
\hat{y} = Xw + b = \begin{pmatrix} y^{(1)} \\ y^{(2)} \\ \dots \\ y^{(m)}\end{pmatrix} =
\begin{pmatrix}
(\sum_{i=1}^{n}{w_ix_i^{(1)}}) + b \\
(\sum_{i=1}^{n}{w_ix_i^{(2)}}) + b \\
\dots \\
(\sum_{i=1}^{n}{w_ix_i^{(m)}}) + b \\
\end{pmatrix}
$$

- Advanced Matrix multiplication:
$$
\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} ax_1 + bx_2 \\ cx_1 + dx_2 \end{pmatrix}
= x_1\begin{pmatrix} a \\ c \end{pmatrix} + x_2\begin{pmatrix} b \\ d \end{pmatrix}
$$

The matrix has transformed the units vectors $\hat{i}$ and $\hat{j}$:

$$
\hat{i} \rightarrow \begin{pmatrix} a \\ c \end{pmatrix},
\hat{j} \rightarrow \begin{pmatrix} b \\ d \end{pmatrix},
$$

### Afternoon: Calculus
**Sum rule**

$$
\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))
$$

**Power rule**

$$
f(x) = x^b
$$
<br/>
$$
f'(x) = bx^{b-1}
$$

**Product rule**

$$
f(x) = g(x)h(x)
$$
<br/>
$$
f'(x) = g'(x)h(x) + g(x)h'(x)
$$

**Quotient rule**
$$
f(x) = \frac {g(x)}{h(x)}
$$
<br/>
$$
f'(x) = \frac {g'(x)h(x) - g(x)h'(x)}{h(x)^2}
$$

**Chain rule**

If $f = f(g)$ and $g=f(x)$ then
$$
\frac{df}{dx} = \frac{df}{dg} \times \frac{dg}{dx}
$$

- Computation graph: implemented forward and backward pass

## Wednesday
### Morning:
- Linear Regression

- Strong assumption on linearity relationship between inputs and targets
- supervised machine learning algorithm
- solves a **regression** problem.
- **Input**: **vector** $x \in R^n$
- **Output**: **scalar** $y \in R$.
- The value that our model predicts y is called $\hat{y}$, which is defined as:

$$
\hat{y} = w_1x_1 + w_2x_2 + \dots + w_nx_n + b = b + \sum^n{w_ix_i} = w^Tx + b
$$

where

$w \in R^n$, and $b \in R$ are parameters

$w$ is the vector of **coefficients**, also known as set of **weights**

$b$ is the **intercept**, also known as the **bias**

$$SSE = \sum_{i=1}^{n}(y - \hat y)^2$$
$$MSE = \frac{1}{n}SSE$$

This is also known as **Ordinary Least Squares (OLS) Linear Regression**

- Gradient Descent

### Afternoon:
- Implement Gradient Descent from scratch
- Interpretability of Linear Regression coefficients

## Wednesday
### Morning: Logistic Regression (Classification)
- Use sigmoid to convert regression output into probability from 0 to 1