# 3D 期末考試筆記

## Reference
- [3D 概論](https://mropengate.blogspot.com/2015/09/3d-introduction-of-3d-graphics-pipeline.html)
- [3D 轉 2D 的方法 (Parallel Projection v.s. Perspective Projection)](https://www.geeksforgeeks.org/difference-between-parallel-and-perspective-projection-in-computer-graphics/)

# Course-1
## Rasterization
光栅化，可以理解為將圖形轉換成以pixel為單位的座標空間，因為我們的顯示器大多是以這樣的方式來顯示的，那其實在在這之間其實還會經過Frame Buffer，你可以想像render都在GPU中，但是我們顯示器是要拿Main Memory的資料來顯示，所以我們在另一塊記憶體用一個Frame Buffer先來存這些render好的圖片，然後在一起傳到Main Memory，然後OS再將資訊交給Window System顯示在螢幕上。

---

## The Rendering Pipeline
- Transform
- Illuminate
- Transform
- Clip
- Project
- Rasterize

---

## Aspect Ratio
計算公式：
- Screen Width / Screen Height
例子：
- 4:3 = 4/3 = 1.3333

---

## Frame Buffer
- Color Buffer
> 通常又分成RGB(紅綠藍)3個channel，Color Buffer的值常使用Unsigned char(0~255)或是Float (0.0f~1.0f) 儲存，值得一提的是常常也會使用4通道RGBA，也就是增加一個「透明」的通道。
- Depth Buffer
> 紀錄該格的深度。所謂的深度是用來紀錄深淺，也就是這個pixel對應的點與相機的距離，因為在一個三維空間中過轉換可能會有兩點重疊，而通常我們傾向
- Stencil Buffer
> 可以決定這個pixel需不需要被繪製，通常是我們只需要部分pixel被繪製，例如被UI檔住，那這部分的pixel就不需要浪費資源去render。

### Memory Calculate
**Buffer size = width \* height \* color depth**
For example:
- If width=640, height=480, color depth=24 bits
> Buffer size = 640 * 480 * 3 = 921,600 bytes
- If width=1920, height=1080, color depth=24 bits
> Buffer size = 1920 * 1080 * 3 = 6,220,800 bytes

---

## Rasterizing Lines
給予畫面上的兩點，然後透過演算法找到這兩點之間對應的其他 pixel，方法有 Midpoint Algorithm

### Midpoint Algorithm
如圖上顯示，今有兩點 P(x,y) & R(x1,y1)，在這PR線上所經過的每一個單位距離都會去計算應該要使用坐標系上的哪一個點
如圖所示，PR線段經過一點 Q，而坐標系上有兩個整數點 NE(x+1,y+1) & E(x+1,y)，以及 NE & E 的中點 M，如果 Q 的 Y 座標在 M 之上，那在 rasterizing 的時候所要使用的就是 NE 點而非 E點

---

## Clipping Problem
### Sutherland-Hodgman Algorithm (2D)
> 該算法從目標多邊形中所有頂點的輸入列表開始。接下來，剪裁多邊形的一條邊在兩個方向上無限延伸，同時遍歷目標多邊形的邊。如果輸入列表中的頂點位於擴展的剪裁多邊形線的可見側，則它們會插入到輸出列表中，並且目標多邊形與剪裁多邊形的延長後的邊相交的頂點會添加到輸出列表。

### 黃林演算法
> 利用點對點之間是否經過 Boundary Clip 有的話，就把找出與圖形的相交點，然後以相交的點建立新的點，其餘的點依此類推。
[參考](http://ir.lib.ntust.edu.tw/retrieve/53067/AN+EFFICIENT+ALGORITHM+FOR+2-D+POLYGON+CLIPPING.pdf)

---
---

# Course-2
## Polygonal Meshes
> 通常一個多邊形會是由 **面** 組成
> 每個點之間必須是 **共面~(coplane)~** \[指幾何形狀落在同一平面上的關係\]
> 3個點可以定義一個平面，但第4個點不必不需要位于該平面上

---

## Polyhedron
> 待補

# Course-3
## Basic Math
- 3 軸被標記為 x, y, z

## Vectors
Points != Vectors
- Point – Point = Vector
- Vector+Vector = Vector
- Point + Vector = Point
- Point + Point = Point

## Point to Point

---
---

# course-4
## Model Transformation
### Scale Matrix

[
Sx    0    0
0     Sy   0
0     0    1
]

### Rotation Matrix

[
cosθ    -sinθ    0
sinθ    cosθ     0
0       0        1
]

#### Rotation for XYZ axis

### Translate Matrix

[
1    0    Tx
0    1    Ty
0    0    1
]

### General Rotation Matrix

## Viewing Transform
- Rotate & translate the world to lie directly in front of the camera
- Typically place camera at origin
- Typically looking down -Z axis
- World 座標 -> View 座標

## Projection Transform
### 投影的種類

### Parallel Projection
水平投影，直接將物體以水平的方式投影到螢幕上

#### Orthographic Projection
正交投影，把物體的每個點透過垂直的方式投影到螢幕上，也就是說投影點到螢幕的向量與螢幕平面上的任意向量垂直 (內積為零)

#### Oblique Projections
與正交投影相反，不垂直投影

### Perspective Projection
透視投影，與光在視網膜成像方式一樣，越近的物體越大

# course-5

# course-6

# course-Animation
## Key Animation
- Easing
- 調整中間幀的時間。可以通過調整參數t的步長來實現自動化。參數，t。

## Interpolation ~(插值)~
- 許多參數可以通過插值來生成動畫
- 簡單的內插技術只能產生簡單的插值
- 更覆雜的插值需要一個更覆雜的動畫對象的模型模擬

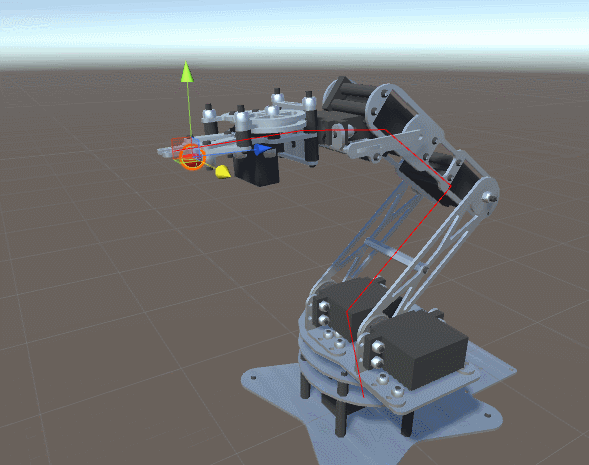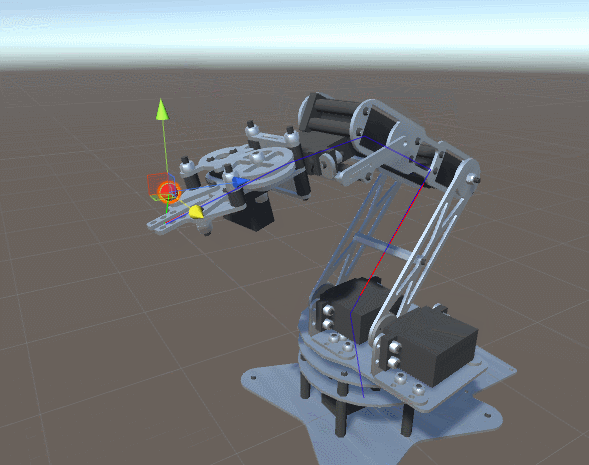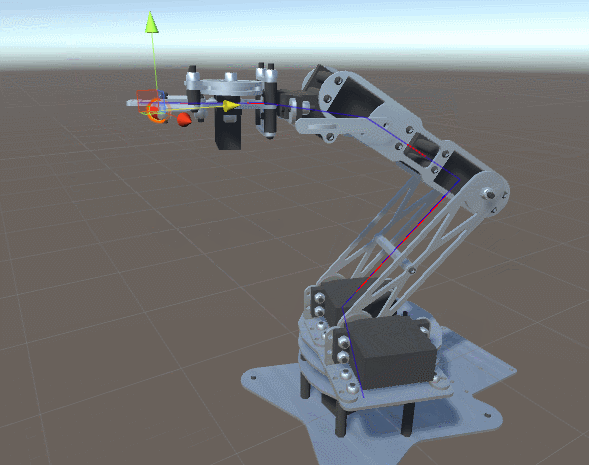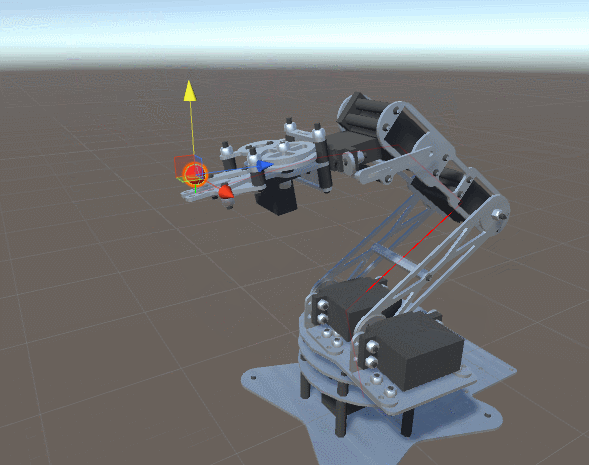
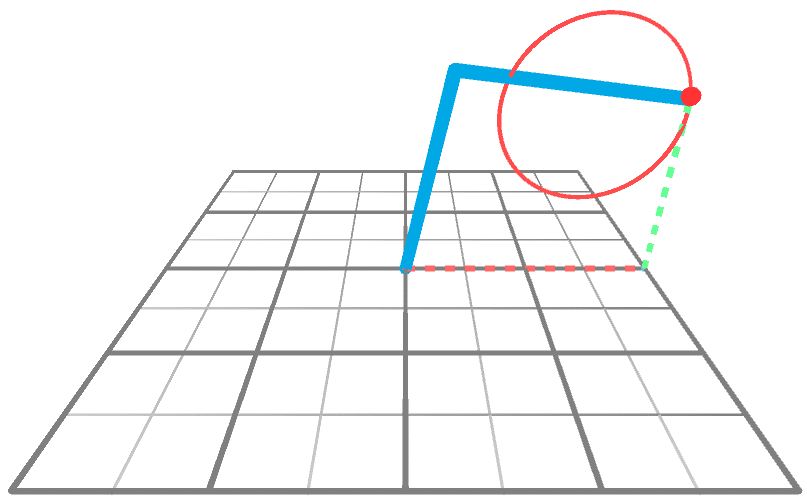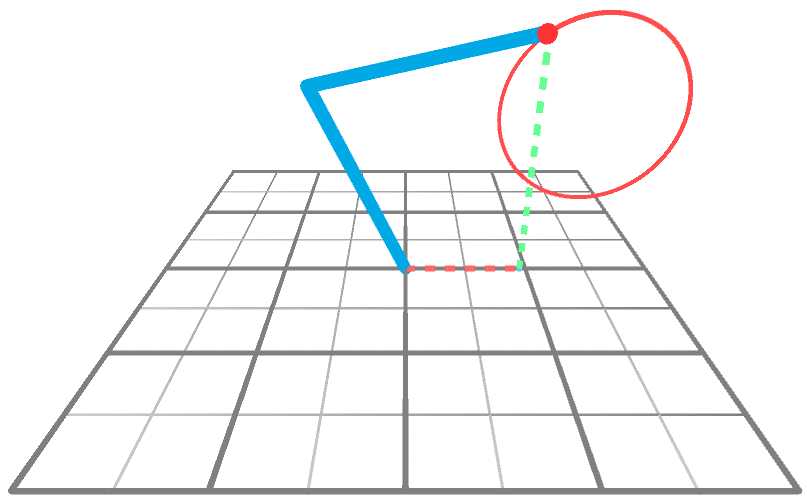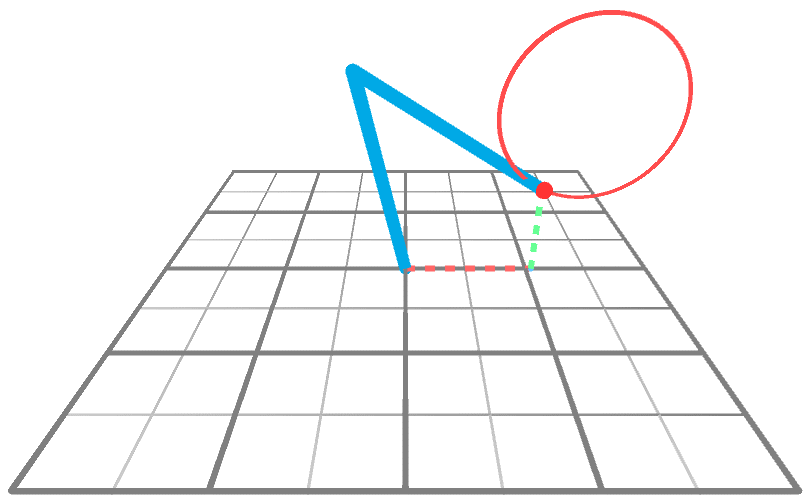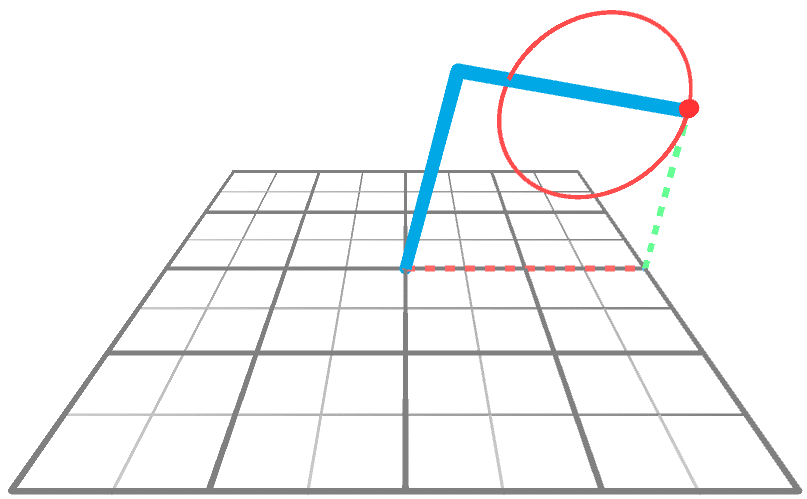
## 動畫技術的 Kinematics
### Forward Kinematics
- 正向動力學可以想成是一個動力傳遞鏈，先算出第一個關節的變化，再根據第一個關節變化去計算第二個關節的變化，以此類推。
- 指定條件（關節角度）
- 計算末端執行器的位置
- 有利於模擬


### Inverse Kinematics
是決定要達成所需要的姿勢所要設置的關節可活動對象的參數的過程
- "目標導向 "的運動
- 指定末端效應器的目標位置
- 有利於控制
- 容易會有無窮解
- 需要限制一些情況來避免無窮解

**<font color="red">逆向運動學提供了更容易的的規範。但它在計算上更加困難</font>**


## 參考
[主題 「資工系選修計算機圖學」之經驗分享](https://home.gamer.com.tw/artwork.php?sn=5171916)
[15animation](https://www.cs.cornell.edu/courses/cs4620/2020fa/slides/15animation.pdf)