###### tags: `ADA 6.3`

# ADA 6.3 Sequence Alignment

:::info
**Longest Common Subseqeunce**
Leetcode: [here](https://leetcode.com/problems/longest-common-subsequence/)

Hope everyone to try to complete it before click the answer.

:::spoiler my answer

#ifndef longest_Common_Subsequence_hpp
#define longest_Common_Subsequence_hpp

#include <stdio.h>
#include <string>
#include <vector>
#include <iostream>

using namespace::std;

namespace LongestCommonSubsequence {
class Soulution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        // opt for time
        return array_longestCommonSubsequence(text1, text2);
//        return vector_longestCommonSubsequence(text1, text2);
    }
    
    int array_longestCommonSubsequence(string text1, string text2) {
        auto m = text1.size();
        auto n = text2.size();
        
        int list[m + 1][n + 1];
        
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j ++) {
                if (i == 0 || j == 0) {
                    list[i][j] = 0;
                }
                else if (text1[i - 1] == text2[j - 1]) {
                    
                    list[i][j] = list[i - 1][j - 1] + 1;
                }
                else {
                    list[i][j] = max(list[i - 1][j], list[i][j - 1]);
                }
            }
        }
        return list[m][n];
    }
    
    int vector_longestCommonSubsequence(string text1, string text2) {
        auto m = text1.size();
        auto n = text2.size();
        
        vector<vector<int>> table;
        vector<int> temp(n + 1);
        table.resize(m + 1, temp);
        
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                
                if (i == 0 || j == 0) {
                    table[i][j] = 0;
                }
                else if (text1[i - 1] == text2[j - 1]) {
                    table[i][j] = table[i - 1][j - 1] + 1;
                }
                else {
                    table[i][j] = max(table[i - 1][j], table[i][j -1]);
                }
            }
        }
            
        cout << backtracking(table, text1, text2) << endl;
        
        return table[m][n];
    }
    
    string backtracking(vector<vector<int>> table, string text1, string text2) {
        auto m = text1.size();
        auto n = text2.size();
        string sub = "";
        
        while (m > 0 && n > 0) {
            if (text1[m - 1] == text2[n - 1]) {
                sub = text1[m - 1] + sub;
                m--;
                n--;
            }
            else if (table[m - 1][n] >  table[m][n - 1]) {
                m--;
            }
            else {
                n--;
            }
        }
        
        return sub;
    }
    
};
}
#endif /* longest_Common_Subsequence_hpp */

:::

:::info
**Edit Distance**
Leetcode: [here](https://leetcode.com/problems/edit-distance/)

Hope everyone to try to complete it before click the answer.

:::spoiler my answer

#ifndef edit_distance_hpp
#define edit_distance_hpp

#include <stdio.h>
#include <iostream>
#include <string>
#include <vector>

using namespace::std;

namespace EditDistance {
class Solution {
public:
    int minDistance(string word1, string word2) {
        return  array_minDistance(word1, word2);
    }
    
    int array_minDistance(string word1, string word2) {
        auto m = word1.size();
        auto n = word2.size();
        
        int list[m + 1][n + 1];
        
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                if (i == 0 && j == 0) {
                    list[0][0] = 0;
                } else if (i == 0) {
                    list[i][j] = list[i][j - 1] + 1;
                } else if (j == 0) {
                    list[i][j] = list[i - 1][j] + 1;
                } else if (word1[i - 1] == word2[j - 1]) {
                    list[i][j] = list[i - 1][j - 1];
                } else {
                    list[i][j] = min(list[i - 1][j - 1], min(list[i][j - 1], list[i - 1][j])) + 1;
                }
            }
        }
        return list[m][n];
    }
};
}
#endif /* edit_distance_hpp */

:::

## Edit Distance


> 兩個字串 - X, Y
> 將 X -> Y 最少的改變
> X 對 Y 逐字比較時，有兩種可能 "相同" 與 "不相同"
> 如果不同時，有三種 case 可以選擇
> 1. 刪除
> 2. 插入
> 3. 替換
> **記住以上的原理來自於 X -> Y 的逐字比較**

相同時：
取上一步 Table[i - 1][j - 1] 的值（因為不需要做任何操作)

不相同時：
- 比較 AllCase
- 取最少的改變 n + 1

### 小結：

- 演算法要考慮兩種，是否要 Backtracking

---

#### Andy 補充於2022/12/20

#### Smith–Waterman algorithm


##### 置換矩陣和空位罰分方法

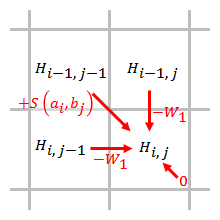
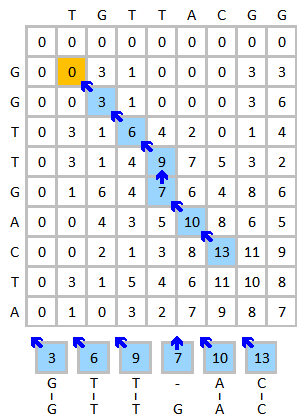
##### 初始化矩陣並填表

##### 完成

##### 回推