# Refresher : Functions
## Problem in Non-Functional Programming
Let's understand the problems arises in Non-Functional programming by taking an example as:
Suppose we have given three integers say a,b,c & we have to calculate the sum of digits of all these numbers seperately. So, the basic program to do that is as shown below.
```java
main(){
--------
--------
int sum1 = 0 , sum2 = 0 , sum3 = 0;
while(a > 0){
sum1 += a % 10;
a /= 10;
}
system.out.println(sum1);
while(b > 0){
sum2 += b % 10;
b /= 10;
}
system.out.println(sum2);
while(c > 0){
sum3 += c % 10;
c /= 10;
}
system.out.println(sum3);
}
```
In the above code, we have to write the same piece of code thrice. So this is the major problem.
The above code have many problems:
* **Redundancy**.
* **Readability**.
* **Maintainability**.
### How to Solve the Above Problems?
We can solve the problems using black box technique as:
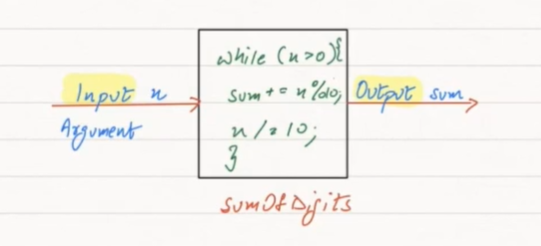
Here, when we require to calculate the sum of digits then we will simply invoke this box and pass the integer in it, then it will return the sum as an output.
When this box is taken together with input and output then this is known as the **function**. By using the function we can overcome the problems mentioned above.
### Syntax of Function
```java
ansType function name(inputType input){
// Main logic.
return ans;
}
```
This is how the typical function looks like.
Let's create a function to sum 2 numbers.
```java
int 2sum(int a,int b){
int sum = a + b;
return sum;
}
```
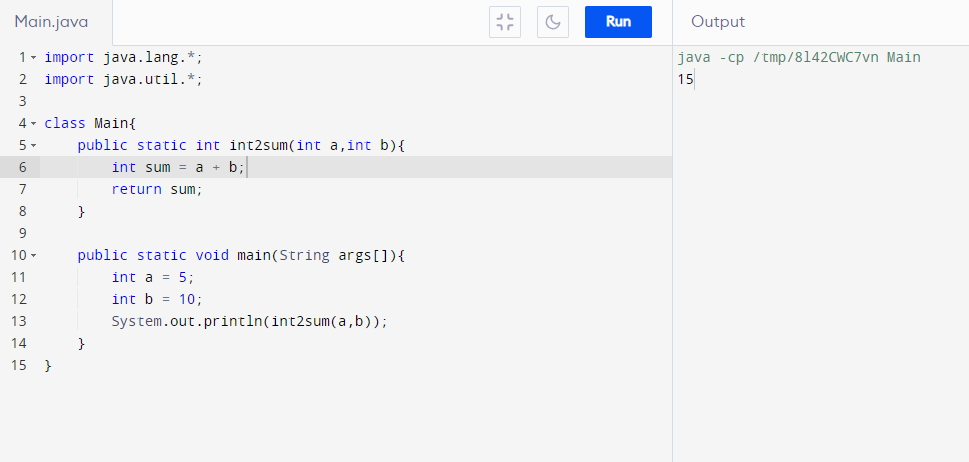
**Note:** In case, the return type is void then no need to return anything(return statement is optional).
---
### Question
What will be the output?
```java
class Test {
public static int sum(int a, int b){
return a + b;
}
public static void main(String[] args){
int a = 15, b = 5;
System.out.println(sum(a, 10));
}
}
```
Choose the correct answer
**Choices**
- [ ] 20
- [x] 25
- [ ] 15
- [ ] 0
**Explanation**
The a & b defined inside the sum function is different from that is defined in the main function. We have passed a & 10 as a argument. that's why the value of b that is defined inside the sum function is 10. Hence, the sum is 25.
---
### Question
What will be the output?
```java
class Test {
public static int sum(int a, int b){
return a + b;
}
public static void main(String[] args){
int a = 15, b = 5;
sum(a,b);
}
}
```
Choose the correct answer
**Choices**
- [ ] 20
- [ ] Error
- [ ] 15
- [x] Nothing will be printed.
**Explanation**
There is not any printing statement like `system.out.print()`. Hence, nothing is printed.
---
### Question
What will be the output?
```java
class Test {
public static int sum(int a, int b){
System.out.print(a + b);
}
public static void main(String[] args){
int a = 15, b = 5;
sum(a,b);
}
}
```
Choose the correct answer
**Choices**
- [ ] 20
- [x] Error
- [ ] 15
- [ ] Nothing will be printed.
**Explanation**
Error because the return type of sum function is int but it does not return anything.
---
### Question
What will be the output?
```java
class Test {
public static int sum(int a, int b){
return a + b;
}
public static void main(String[] args){
int a = 15, b = 5;
System.out.println(sum(20, b));
}
}
```
Choose the correct answer
**Choices**
- [ ] 20
- [ ] Error
- [x] 25
- [ ] Nothing will be printed.
---
### Question
What will be the output?
```java
class Test {
public static int sum(int a, int b){
return a + b;
}
public static void main(String[] args){
int a = 15, b = 5;
System.out.println(sum(6, 10));
}
}
```
Choose the correct answer
**Choices**
- [ ] 20
- [ ] Error
- [x] 16
---
## Question 1
Given an integer **N**, return whether the integer is even or not.
#### TestCase
##### Input 1
```plaintext
12
```
##### Output 1
```plaintext
true
```
##### Input 2
```plaintext
5
```
##### Output 2
```plaintext
false
```
### PseudoCode
```java
public static boolean iseven(int n){
if(n % 2 == 0) return true;
else return false;
}
```
---
## Question 2
Given an integer **N**, return whether its height is small, medium or large.
* if it is less than 10, then its small.
* if it is between 10 to 20, then its medium.
* if it is greater than 20, then large.
#### TestCase
##### Input 1
```plaintext
5
```
##### Output 1
```plaintext
small
```
##### Input 2
```plaintext
51
```
##### Output 2
```plaintext
large
```
### PseudoCode
```java
public static String height(int n){
if(n < 10) return "small";
else if(n < 20) return "medium";
else return "large".
}
```
---
## Question 3
Given two doubles as argument, return the area of the rectangle.
#### TestCase
##### Input 1
```plaintext
1.0
2.0
```
##### Output 1
```plaintext
2.0
```
### PseudoCode
```java
public static double areaofrectangle(double a, double b){
double area = a * b;
return area;
}
```
---
## Question 4
Given the radius(double) of the circle, return the area of the circle.
#### TestCase
##### Input 1
```plaintext
7.0
```
##### Output 1
```plaintext
154.0
```
### PseudoCode
```java
public static double areaofcircle(double radius){
double area = 3.14 * radius * radius;
return area;
}
```
**Note:** Instead of writing the value of PI as 3.14, we can directly use the module Math.PI. To use that we have to import the maths library.
---
## Question 5
Given an integer **N** as an input, print all the prime numbers between 1 to N.
#### TestCase
##### Input 1
```plaintext
10
```
##### Output 1
```plaintext
2 3 5 7
```
#### Explanation
Prime number is the number which is not divisible by any oof the number except 1 and itself. So, to find the number of prime numbers between 1 to **N**, just count the number of itegers which divides it. if it is equal to 2 then it is prime number.
#### PseudoCode
```java
public static void primenumbers(int n) {
for (int num = 1; num <= n; num++) {
int factors = 0;
for (int i = 1; i <= num; i++) {
if (num % i == 0) factors++;
}
if (factors == 2) system.out.print(num);
}
}
```
We can further break it as:
```java
public static boolean isprime(int n) {
int factors = 0;
for (int i = 1; i <= num; i++) {
if (num % i == 0) factors++;
}
if (factors == 2) return true;
else return false;
}
public static void primenumbers(int n) {
for (int num = 1; num <= n; num++) {
if (isprime(num)) system.out.print(num);
}
}
```