# Heap Heap是一種特殊的基於樹的數據結構，其中樹是完全二叉樹。 --- # Binary Heap ## Max-Heap -操作 -演算法 ## Min-Heap -操作 -演算法 --- A Binary Heap is a Binary Tree with following properties.(下列屬性) --- 1) It’s a complete tree (All levels are completely filled except possibly the last level and the last level has all keys as left as possible). This property of Binary Heap makes them suitable to be stored in an array. 翻譯: 這是一棵完全的樹（除了可能的最後一層，所有level都完全填滿，最後一層的所有鍵都盡可能左）。 二叉堆的這一特性使它們適合存儲在數組中。 --- 2) A Binary Heap is either Min Heap or Max Heap. In a Min Binary Heap, the key at root must be minimum among all keys present in Binary Heap. The same property must be recursively true for all nodes in Binary Tree. Max Binary Heap is similar to MinHeap. 翻譯: 二叉堆是最小堆或最大堆。 在最小二叉堆中，根處的鍵必須是二叉堆中所有鍵中的最小值。 對於二叉樹中的所有節點，相同的屬性必須遞歸地為真。 Max Binary Heap 類似於 MinHeap。 --- 給定Heap中任意節點P和C，若P是C的母節點，那麼P的值會小於等於（或大於等於）C的值。 --- 若母節點的值恆小於等於子節點的值，此堆積稱為最小堆積（min heap）；  --- 反之，若母節點的值恆大於等於子節點的值，此堆積稱為最大堆積（max heap）。  --- 在堆積中最頂端的那一個節點，稱作根節點（root node），根節點本身沒有母節點（parent node）。 以Array看:root node 的index=0 --- Binary Heap 有幾種特性： 每個 node 最多有兩個 child同一階層要由左到右排列，不能跳過。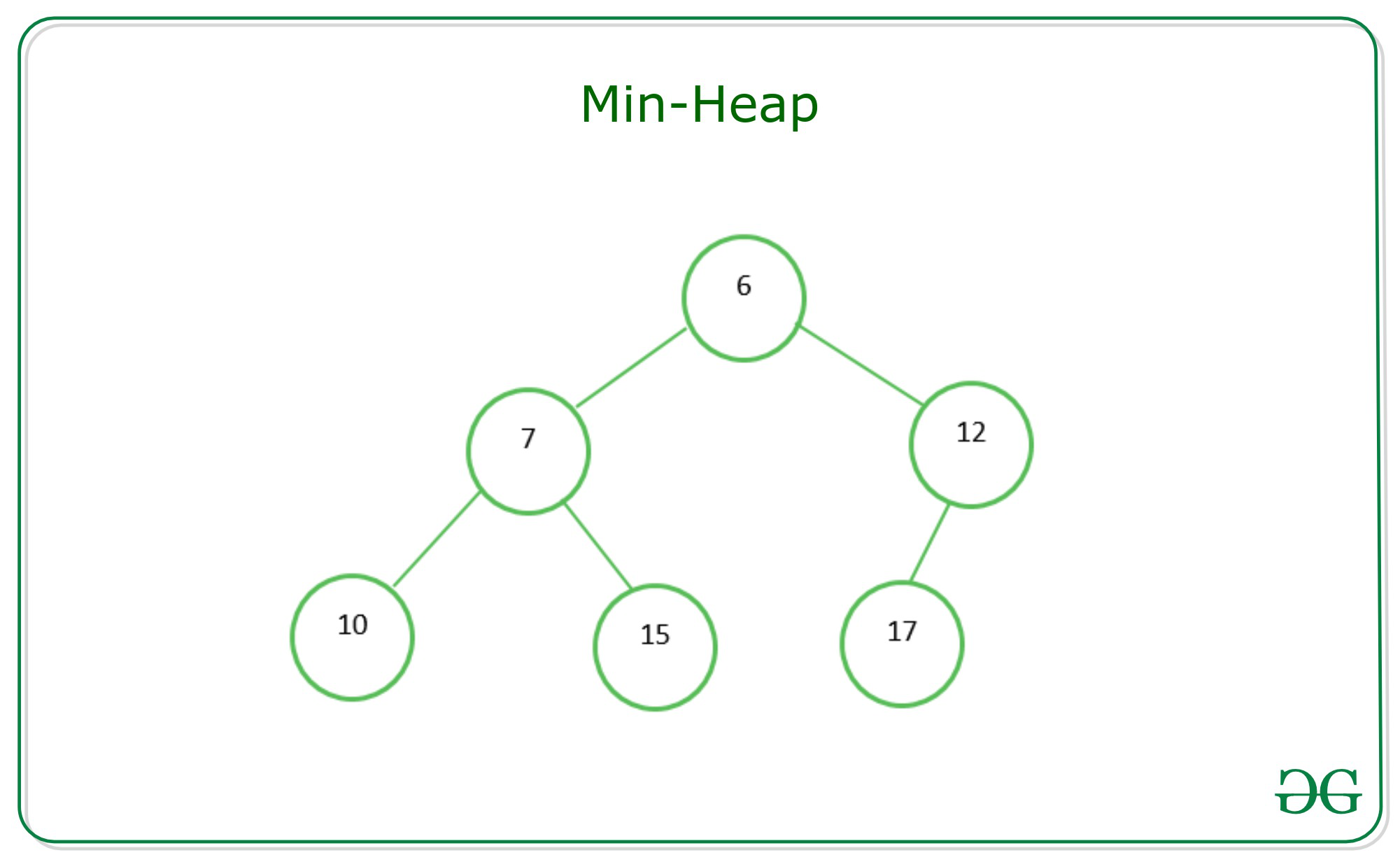 --- eg: 下圖的底層 2, 7 一定要與 17 相連，如果要新增元素的話，因為 17 已經連滿，再來是要與 3 連，依序從左到右  --- 如果是 max-heap 的話，每個 node 都要比自己 child 大， （max-heap）root 就會是整個 heap 的最大值 --- 如果是 min-heap 反之（下圖是 min-heap ） （min-heap）root 就會是整個 heap 的最小值 ---  --- index number =0 開始 除root=Arr[0] Arr[(i -1) / 2] returns its parent node. Arr[(2 * i) + 1] returns its left child node. Arr[(2 * i) + 2] returns its right child node. --- min-heap operations |Method|Time Complexity| |-----|--------| |getMin()|O(1)| |extractMin()[1]|O(Log n)| |insert()|O(Log n)| [1]heapify() ---  ---  --- Max heap operations |Method|Time Complexity| |-----|--------| |getMax()|O(1)| |extractMax()[1]|O(Log n)| |insert()|O(Log n)| [1]heapify() --- heapify() Algorithm psudo-code ``` heapify(array){ Root = array[0] Largest = largest( array[0] , array [2 * 0 + 1]. array[2 * 0 + 2]) if(Root != Largest){ Swap(Root, Largest) } } ``` --- heapify() ```java= // To heapify a subtree rooted with node i which is // an index in arr[]. n is size of heap void heapify(int arr[], int n, int i) { int largest = i; // Initialize largest as root int l = 2 * i + 1; // left = 2*i + 1 int r = 2 * i + 2; // right = 2*i + 2 // If left child is larger than root if (l < n && arr[l] > arr[largest]) largest = l; // If right child is larger than largest so far if (r < n && arr[r] > arr[largest]) largest = r; // If largest is not root if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // Recursively heapify the affected sub-tree heapify(arr, n, largest); } } ``` --- Heap 是被發明來做 [Heap Sort](https://www.geeksforgeeks.org/heap-sort/) 的，在 time complexity 有到達 O(nlog(n)) 但在實務上還是使用 [Quicksort](https://www.geeksforgeeks.org/quick-sort/?ref=gcse) 為主 WHY? --- A Binary Heap is a Complete Binary Tree. A binary heap is typically represented as an array. 二叉堆是一棵完全二叉樹。二叉堆通常表示為一個array。 --- The traversal method use to achieve Array representation is Level Order 實現Array表示的遍歷方法是Level Order --- level order 以下圖為例，我們從根節點出發，也就是 8，依序從每個 Level (也就是 Level Order) 從左到右地走訪，照此邏輯我們會得到 8>3>10>1>6>14>4>7>13  --- Heap vs Priority Queue |Heap |Priority Queue| |-----|--------| |特定樹的數據結構|基本queue結構 | |以排序形式存儲 |以簡單的形式存儲 | 我們使用 PriorityQueue 類在 Java 中實現heap。默認情況下，Min Heap 由此類實現。 --- 練: https://leetcode.com/problems/relative-ranks/ score給你一個大小為 的整數數組n，其中score[i]是運動員在比賽中的得分。 **所有的分數都保證是唯一的**。 運動員根據他們的分數進行排名，運動員得分最高的地方，運動員得分最高的地方，依此類推。每個運動員的位置決定了他們的排名：1st,2nd,3nd --- ```java= class Solution { public String[] findRelativeRanks(int[] score) { int n = score.length; String[] res = new String[n]; PriorityQueue<Integer> pq = new PriorityQueue<>((a,b)->score[a]-score[b]); for(int i=0;i<n;i++){ pq.add(i); } int i=1; while(!pq.isEmpty()){ int idx = pq.poll(); if(i>3){ res[idx] = Integer.toString(i); }else if(i==1){ res[idx] = "Gold Medal"; }else if(i==2){ res[idx] = "Silver Medal"; }else if(i==3){ res[idx] = "Bronze Medal"; } i++; } return res; } } ``` --- 練: https://leetcode.com/problems/maximum-product-of-two-elements-in-an-array/ 1464 . 數組中兩個元素的最大乘積 給定整數數組nums，您將選擇該數組的兩個不同索引i和j。返回 的最大值 (nums[i]-1)*(nums[j]-1)。 --- ```java= class Solution { public int maxProduct(int[] nums) { PriorityQueue<Integer> pq = new PriorityQueue<>(Collections.reverseOrder()); //在Java中，Priority Queue默認實現了min Priority Queue，如果我們需要將Priority Queue的順序從min改成max Priority Queue for (int i =0;i<nums.length;i++){ pq.add(nums[i]); } int n1 = pq.poll(); int n2 = pq.poll(); return (n1-1)*(n2-1); } } ```