# Exercises Parallel Python 2024-03 - day 2
# 5. Delayed evaluation
---
:::info
### Challenge: Run the workflow
Given this workflow:
```python
x_p = add(1, 2)
y_p = add(x_p, 3)
z_p = add(x_p, -3)
```
Visualize and compute `y_p` and `z_p` separately, how many times is `x_p` evaluated?
Now change the workflow:
```python
x_p = add(1, 2)
y_p = add(x_p, 3)
z_p = add(x_p, y_p)
z_p.visualize(rankdir="LR")
```
We pass the not-yet-computed promise `x_p`to both `y_p`and `z_p`. Now, only compute `z_p`, how many times do you expect `x_p` to be evaluated? Run the workflow to check your answer.
:::
---
:::info
### Challenge: Understand our gather function
```python
@delayed
def gather(*arg):
return list(arg)
```
Can you describe what the gather function does in terms of lists and promises?
Hint: Suppose I have a list of promises, what does `gather` allow me to do?
:::
---
:::info
### Challenge: Design a mean function and calculate $\pi$
Write a delayed function that computes the mean of its arguments. Use it to esimates $\pi$ several times and returns the mean of the results.
```python
>>> mean(1, 2, 3, 4).compute()
2.5
```
Make sure that the entire computation is contained in a single promise.
Here is the function to estimate $\pi$ from N random samples:
```python
import random
def calc_pi(N):
"""Computes the value of pi using N random samples."""
M = 0
for i in range(N):
# take a sample
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
if x*x + y*y < 1.: M+=1
return 4 * M / N
```
:::
# 6. Map and reduce
:::info
### Challenge: difference between `filter` and `map`
Without executing it, try to forecast what would be the output of `bag.map(pred).compute()`.
:::
---
:::info
### Challenge: consider `pluck`
We previously discussed some generic operations on bags. In the documentation, lookup the `pluck` method. How would you implement this if `pluck` wasn’t there?
hint: Try `pluck` on some example data, for instance:
```python=
from dask import bags as db
data = [
{ "name": "John", "age": 42 },
{ "name": "Mary", "age": 35 },
{ "name": "Paul", "age": 78 },
{ "name": "Julia", "age": 10 }
]
bag = db.from_sequence(data)
...
```
:::
---
:::info
### Challenge: dask version of pi estimation
Use `map` and `mean` functions on Dask bags to compute 𝜋.
:::
# 7. AsyncIO
:::info
## Challenge: generate all even numbers
Can you write a generator that generates all even numbers? Try to reuse `integers()`. Extra: Can you generate the Fibonacci numbers?
:::
:::spoiler
```python
def even_integers():
for i in integers():
if i % 2 == 0:
yield i
```
or
```python
def even_integers():
return (i for i in integers() if i % 2 == 0)
```
For the Fibonacci numbers:
```python
def fib():
a, b = 1, 1
while True:
yield a
a, b = b, a + b
```
:::
---
:::info
## Challenge: line numbers
Change `printer` to add line numbers to the output.
:::
---
:::info
## Gather multiple outcomes
We've seen that we can gather multiple coroutines using `asyncio.gather`. Now gather several `calc_pi` computations, and time them.
:::
:::spoiler
```python
async with timer() as t:
result = await asyncio.gather(
asyncio.to_thread(calc_pi, 10**7),
asyncio.to_thread(calc_pi, 10**7))
```
:::
---
:::info
## Compute $\pi$ in a script
Collect what we have done so far to compute $\pi$ in parallel into a script and run it.
:::
# 8. Mandelbrot
This exercise uses Numpy and Matplotlib.
```python
from matplotlib import pyplot as plt
import numpy as np
```
We will be computing the famous [Mandelbrot
fractal](https://en.wikipedia.org/wiki/Mandelbrot_fractal).
:::info
## Complex numbers
Complex numbers are a special representation of rotations and scalings in the two-dimensional plane. Multiplying two complex numbers is the same as taking a point, rotate it by an angle $\phi$ and scale it by the absolute value. Multiplying with a number $z \in \mathbb{C}$ by 1 preserves $z$. Multiplying a point at $i = (0, 1)$ (having a positive angle of 90 degrees and absolute value 1), rotates it anti-clockwise by 90 degrees. Then you might see that $i^2 = (-1, 0)$. The funny thing is, that we can treat $i$ as any ordinary number, and all our algebra still works out. This is actually nothing short of a miracle! We can write a complex number
$$z = x + iy,$$
remember that $i^2 = -1$ and act as if everything is normal!
:::
The Mandelbrot set is the set of complex numbers $$c \in \mathbb{C}$$ for which the iteration,
$$z_{n+1} = z_n^2 + c,$$
converges, starting iteration at $z_0 = 0$. We can visualize the Mandelbrot set by plotting the
number of iterations needed for the absolute value $|z_n|$ to exceed 2 (for which it can be shown
that the iteration always diverges).
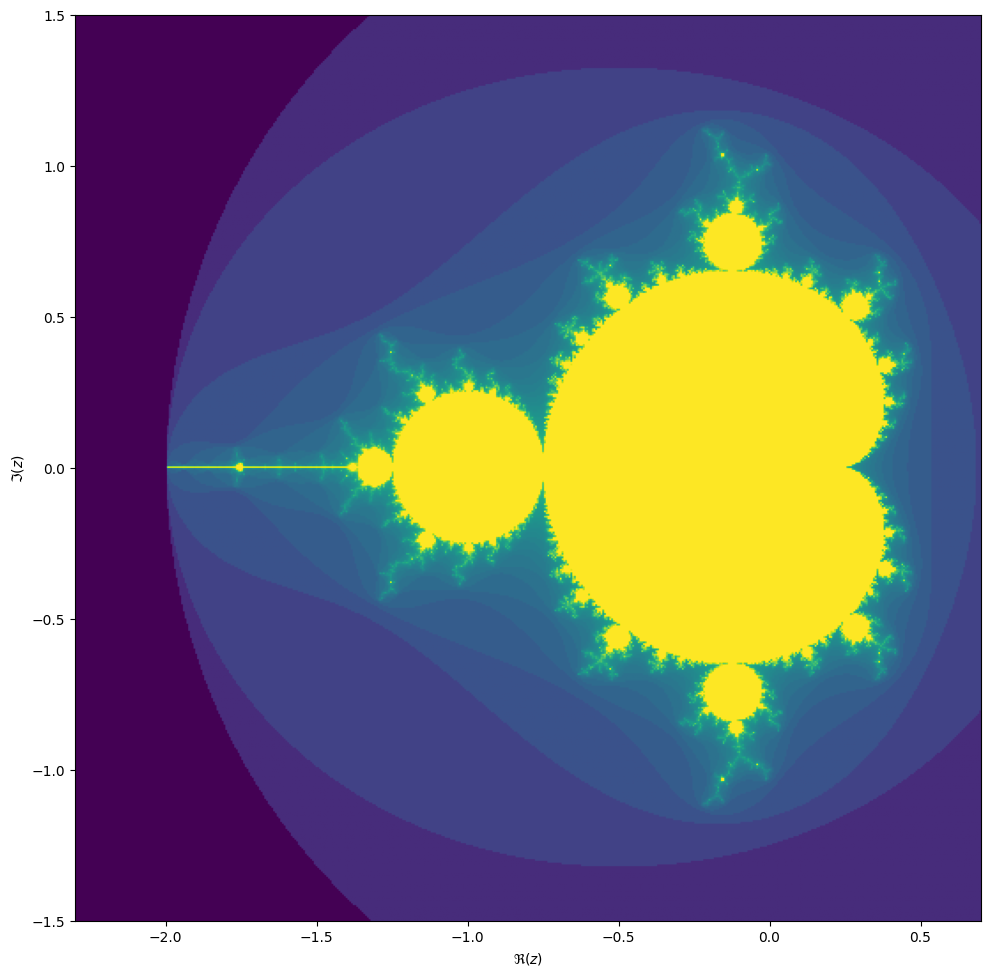
We may compute the Mandelbrot as follows:
```python
max_iter = 256
width = 256
height = 256
center = -0.8+0.0j
extent = 3.0+3.0j
scale = max((extent / width).real, (extent / height).imag)
result = np.zeros((height, width), int)
for j in range(height):
for i in range(width):
c = center + (i - width // 2 + (j - height // 2)*1j) * scale
z = 0
for k in range(max_iter):
z = z**2 + c
if (z * z.conjugate()).real > 4.0:
break
result[j, i] = k
```
Then we can plot with the following code:
```python
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
plot_extent = (width + 1j * height) * scale
z1 = center - plot_extent / 2
z2 = z1 + plot_extent
ax.imshow(result**(1/3), origin='lower', extent=(z1.real, z2.real, z1.imag, z2.imag))
ax.set_xlabel("$\Re(c)$")
ax.set_ylabel("$\Im(c)$")
```
Things become really loads of fun when we start to zoom in. We can play around with the `center` and
`extent` values (and necessarily `max_iter`) to control our window.
```python
max_iter = 1024
center = -1.1195+0.2718j
extent = 0.005+0.005j
```
When we zoom in on the Mandelbrot fractal, we get smaller copies of the larger set!
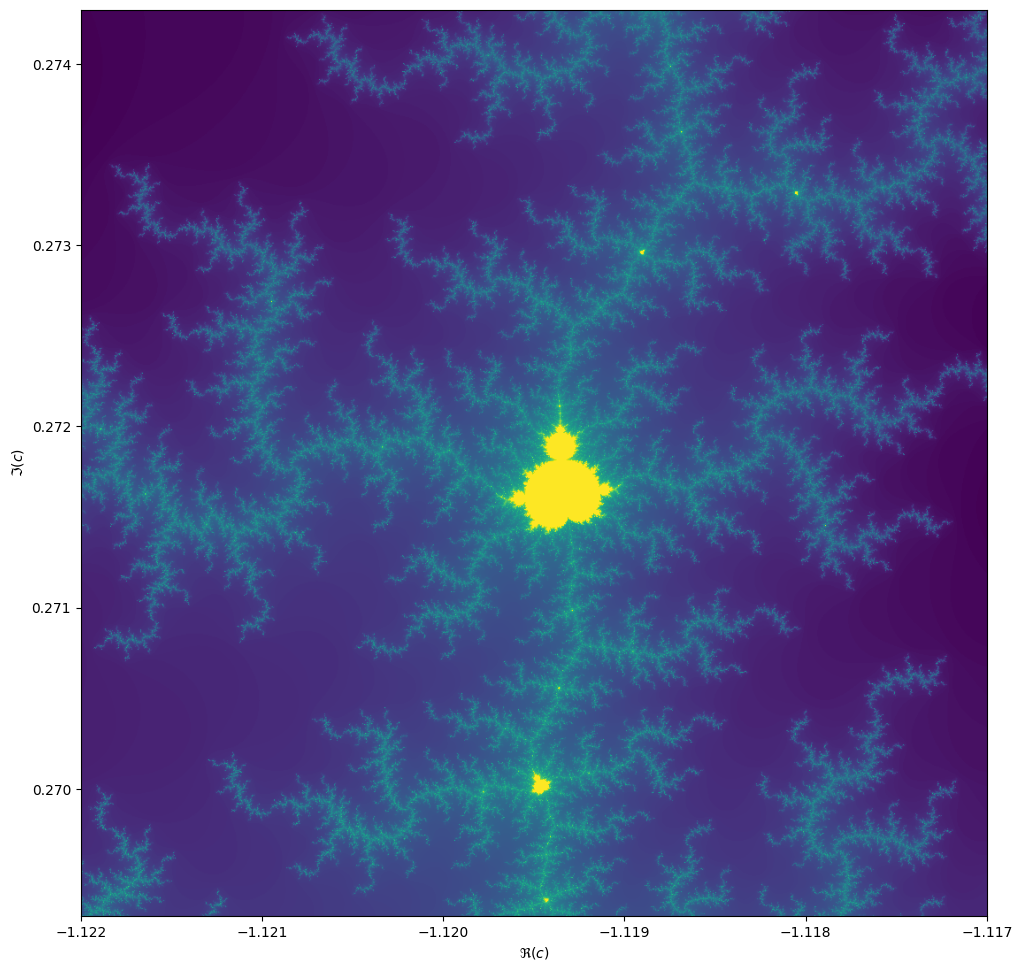
:::info
## Exercise
Make this into an efficient parallel program. What kind of speed-ups do you get?
:::