# 競プロ講習会第4回 Web資料
## ◎第4回の参加方法について
今回も、好きな時間に問題を解いておくことができるようにします。
講習会開始後30分は問題を解く時間に充てますが、ちゃんと時間を取って解きたい人は以下の方法で事前に参加してください。
まず、Codeforcesにログインします。
その後、K-LMSに公開したコンテストリンクを開きます。
KeioAICKyoproCourseContest #4 に、**Virtual participation**します。
(※この機能は、好きな時間を選んでコンテストに参加できる機能です)
開始したい時間を入力し、Registar for virtual participationを押します。
指定した時間になったらコンテストが始まるので、問題を解きます。
コンテストの時間終了後、講習会前であっても解き直しなど自由に行っていただいて構いません。
また、参加中であってもweb資料のヒント・解説は参照してかまいません。
Slackの公開チャンネルやDMでの質問も受け付けますのでお気軽にどうぞ(すぐに答えられるとは限りませんがご了承ください)。
#### ◎問題セット
https://codeforces.com/contestInvitation/74cec6ce97b1e394f1cc5873e6913b7e36ef1829
#### ◎公式解説
##### A〜F問題
https://codeforces.com/blog/entry/64130
##### G問題
https://codeforces.com/blog/entry/92582
## ◎問題訳(意訳あり注意)
### ◎A. Repeating Cipher
TL:1s ML:256MB
#### ●問題
Polycarpはサイファー(文章を読み辛くする暗号化)が大好きです。彼は、"repeating"というサイファーを発明しました。
文字列 $s = s_1s_2...s_m\ (1 \le m \le 10)$ がある時、以下のように暗号化します。
・$s_1$ を 1回書く。
・$s_2$ を 2回書く。
・$s_3$ を 3回書く。
……
・$s_m$ を $m$ 回書く。
例えば、$s$ = "bab" の時、 "b" → "baa" → "baabbb" と暗号化が進み、暗号文は "baabbb" になります。
ある文字列 $s$ を暗号化した暗号文 $t$ が与えられます。複号化し、$s$ を求めてください。
#### ●入力
1行目には、整数 $n (1 \le n \le 55)$ が与えられます。これは暗号文 $t$ の長さです。
2行目に、長さ $n$ の暗号文 $t$ が与えられます。$t$ は英小文字のみで構成されています。
答えは常に一意に存在することが保障されています。
#### ●出力
$t$ を復号化した $s$を出力し、改行してください。
#### ●入出力例
##### 入力例1
```
6
baabbb
```
##### 出力例1
```
bab
```
##### 入力例2
```
10
ooopppssss
```
##### 出力例2
```
oops
```
##### 入力例3
```
1
z
```
##### 出力例3
```
z
```
### ◎B. Array Stabilization
TL:1s ML:256MB
#### ●問題
$n$ 個の整数からなる配列 $a$ が与えられます。
配列の**不安定さ**を次の値で定義します。
$$
\max_{i = 1}^n a_i - \min_{i = 1}^n a_i
$$
つまり、不安定さは配列の最大値と最小値の差です。
あなたはちょうど一つの要素をこの配列から削除し、残りの$n-1$要素からなる配列の**不安定さ**を最小にしたいです。
最小の**不安定さ**としてありえる値を求めてください。
#### ●入力
1行目には、整数 $n (2 \leq n \leq 10^5)$ が与えられます。これは配列 $a$ に含まれる要素の数です。
2行目には、$n$ 個の整数 $a_1, a_2, \ldots, a_n(1 \leq a_i \leq 10^5)$ が与えられます。それぞれ配列 $a$ の要素です。
#### ●出力
1つの整数を出力してください。
その整数は、$a$ から要素を1つ削除した配列の不安定さとしてありえるものの最小値です。
#### ●入出力例
##### 入力例1
```
4
1 3 3 7
```
##### 出力例1
```
2
```
7 を削除して得られる配列は `[1, 3, 3]` で、不安定さは2です。
削除することで2よりも不安定さが小さくなる要素はないので、答えは2になります。
##### 入力例2
```
2
1 100000
```
##### 出力例2
```
0
```
削除する要素として1、100000のどちらを選んでも、配列の要素が1つになり不安定さは0になります。
### ◎C. Powers Of Two
TL:4s ML:256MB
#### ●問題
正の整数 $x$ は、 ある非負整数 $y$ を用いて $x = 2^y$ と表せるとき、またその時に限り `power of two` であるとします。
つまり、`power of two` である整数は、 $1,2,4,8,16, ...$ です。
正の整数 $n,k$ が与えらえます。 $n$ をちょうど $k$ 個の `power of two` の和で表してください。
#### ●入力
二つの整数 $n,k (1 \le n \le 10^9 , 1 \le k \le 2 \times 10^5)$ が1行目に空白区切りで与えられる。
#### ●出力
もし、$n$ をちょうど $k$ 個の `power of two` の和で表せないのなら、 `NO` を出力してください。
そうでなければ、1行目に `YES` を出力したのち、 2行目に $k$ 個の数字 $b_1,b_2,...,b_k$ を空白区切りで出力してください。
$b_1 + b_2 + ... + b_k = n$ かつ、 $b_i$ は `power of two` である必要があります。
答えが複数通り考えられる場合、いずれを出力しても構いません。
#### ●入出力例
##### 入力例1
```
9 4
```
##### 出力例1
```
YES
1 2 2 4
```
##### 入力例2
```
8 1
```
##### 出力例2
```
YES
8
```
##### 入力例3
```
5 1
```
##### 出力例3
```
NO
```
##### 入力例4
```
3 7
```
##### 出力例4
```
NO
```
### ◎D. Circular Dance
TL:3s ML:256MB
#### ●問題
$n$ 人の子どもがクリスマスツリーを囲んで円形になり時計回りの方向を向いて踊っています。
子ども達には、時計回りに $p_1, p_2, \ldots, p_n$ として番号がつけられています。 $p_i$ はそれぞれ $1$ から $n$ の異なる整数で、順列になっています。
$i < n$ のときは子ども $p_i$ の前の子どもは $p_{i + 1}$ であり、$i = n$ のときは $p_i$ の前の子どもは $p_1$ になります。
ダンスが終わったあと、それぞれの子どもは自分の前にいた子ども $x$ と、$x$ の前にいた子どもを覚えていました。
つまり、子ども $i$ は子ども $a_{i, 1}$ と $a_{i, 2}$ を覚えていますが、$a_{i, 1}$ と $a_{i, 2}$ は円形に並んでいるときの順番とは限りません。
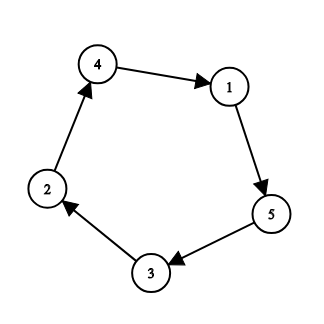
この例では `p = [3, 2, 4, 1, 5]` です。子どもが覚えている情報としては次のようなものがありえます。
$a_{1, 1} = 3, a_{1, 2} = 5; a_{2, 1} = 1, a_{2, 2} = 4; a_{3, 1} = 2, a_{3, 2} = 4; a_{4, 1} = 1, a_{4, 2} = 5; a_{5, 1} = 2, a_{5, 2} = 3;$
あなたは、この情報をもとに円形に並んでいた子ども達の順番を復元してください。複数の答えがあるときはそのうちの一つを出力してください。
少なくとも1つの答えがあることは保証されます。
**Pythonを利用している場合、提出するときに Python ではなく PyPy を選択してください。**
#### ●入力
1行目には、整数 $n (3 \leq n \leq 2 \cdot 10^5)$ が与えられます。これは子ども達の人数です。
続く $n$ 行に2つの整数が与えられます。
$i$ 行目には、2つの整数 $a_{i, 1}, a_{i, 2}(1 \leq a_{i, 1}, a_{i, 2} \leq n, a_{i, 1} \neq a_{i, 2})$ が与えられます。
これは、$i$ 番の子どもが覚えている子どもの番号で、$a_{i, 1}$ と $a_{i, 2}$ の順番は任意です。
#### ●出力
$n$ 個の整数 $p_1, p_2, \ldots, p_n$ を出力してください。
これは、$1$ から $n$ の順列であって、円形に並んでいる子どもの順番に対応しています。
もしも複数の答えがありえるときには、その中のどの答えを出力しても構いません。例えば、円形に並んでいる子どもの誰を先頭として扱うかは関係ありません。
少なくとも1つの答えがあることが保証されます。
#### ●入出力例
##### 入力例1
```
5
3 5
1 4
2 4
1 5
2 3
```
画像の例になります。
##### 出力例1
```
3 2 4 1 5
```
##### 入力例2
```
3
2 3
3 1
1 2
```
##### 出力例2
```
3 1 2
```
### ◎E. Almost Regular Bracket Sequence
TL:3s ML:256MB
#### ●問題
$n$ 文字の括弧列 $s$ が与えられます。ここで括弧列とは '(' と ')' のみを用いた文字列のことを指します。
標準括弧列とは、'1'と'+' を適切な位置に挿入することで、正しい数学的表現になるような括弧列のことを指します。
例1: "()()" → "(1)+(1)" なので標準括弧列
例2: "(())" → "((1+1)+1)" なので標準括弧列
例3: ")(" は標準括弧列ではない
例4: "(" は標準括弧列ではない
あなたは、ある $i$ を選んで、$i$ 文字目の括弧を反転することができます。
より具体的には、 $s_i$ = '(' の時、 $s_i$ = ')' に反転できます。逆も同様です。
全ての $i (1 \le i \le n)$ のうち、$s_i$ を反転させた際に $s$ が標準括弧列となるような整数 $i$ がいくつ存在するか答えてください。
#### ●入力
1行目に、 1つの整数 $n(1 \le n \le 10^6)$ が与えられる。これは、$s$ の長さを示す。
2行目に、 長さ $n$ の括弧列 $s$ が与えられる。
#### ●出力
全ての $i (1 \le i \le n)$ のうち、$s_i$ を反転させた際に $s$ が標準括弧列となるような整数 $i$ の個数を求め、1行目に出力し、改行してください。
#### ●入出力例
##### 入力例1
```
6
(((())
```
##### 出力例1
```
3
```
##### 入力例2
```
6
()()()
```
##### 出力例2
```
0
```
##### 入力例3
```
1
)
```
##### 出力例3
```
0
```
##### 入力例4
```
8
)))(((((
```
##### 出力例4
```
0
```
### ◎F. Make It Connected
TL:2s ML:256MB
#### ●問題
$n$ 頂点からなる無向グラフが与えられます。各頂点 $i$ には整数 $a_i$ が書かれており、最初はグラフに辺がありません。
あなたはグラフにいくつかの辺を追加することができますが、コストがかかります。頂点 $x$ と $y$ を結ぶ辺を追加するときにかかるコストは $a_x + a_y$ コインです。
もう1つの方法として特別なオファーが $m$ 個あり、それぞれのオファーは3つの整数 $x, y, w$ で表されます。これは、頂点 $x, y$ を結ぶ辺を $w$ コイン払うことで追加できることを意味しています。
特別なオファーを必ずしも使う必要はなく、$x, y$ を結ぶ辺を追加できるオファーがあったとしても $w$ コインを払う代わりに $a_x + a_y$ コイン払うことで辺を追加することができます。
#### ●入力
1行目には、2つの整数 $n, m(1 \leq n \leq 2 \cdot 10^5, 0 \leq m \leq 2 \cdot 10^5)$ が与えられます。これは、グラフの頂点数と特別なオファーの数です。
2行目には、$n$ 個の整数 $a_1, a_2, \ldots, a_n(1 \leq a_i \leq 10^{12})$ が与えられます。これは、グラフの各頂点に書かれた整数です。
続く $m$ 行には、それぞれ 3つの整数 $x, y, w(1 \leq x, y, \leq n, 1 \leq w \leq 10^{12}, x \neq y)$ が与えられます。これは特別なオファーを表しており、あなたは頂点 $x, y$ を結ぶ辺を $w$ コイン払うことで追加することができます。
#### ●出力
1つの整数を出力してください。
この整数は、グラフを連結にするために払う必要があるコインの数の最小値です。
#### ●入出力例
##### 入力例1
```
3 2
1 3 3
2 3 5
2 1 1
```
##### 出力例1
```
5
```
2つ目の特別なオファーを使って、1枚のコインで頂点 $1, 2$ を結ぶ辺を追加し、オファーを使わずに $4$ 枚のコインで頂点 $1, 3$ を結ぶ辺を追加することで連結にできます。
##### 入力例2
```
4 0
1 3 3 7
```
##### 出力例2
```
16
```
特別なオファーを使わずに、最適解が達成できます。
##### 入力例3
```
5 4
1 2 3 4 5
1 2 8
1 3 10
1 4 7
1 5 15
```
##### 出力例3
```
18
```
特別なオファーを使わずに、最適解が達成できます。
### ◎G. The Final Pursuit
TL:3s ML:256MB
#### ●問題
$n$次元ハイパーキューブとは、無向重み無しグラフで、以下のように再帰的に定義されるグラフのことを指します。
・$0$ 次元ハイパーキューブは、頂点1つで辺の無いグラフである。この頂点には、0の番号が付けられている。
・$n(>0)$ 次元ハイパーキューブは以下のように構成されるグラフである。
$(n-1)$次元ハイパーキューブを2つ用意し、$a,b$ とする。$a,b$ に存在する、同じ番号が書かれた全ての頂点のペア($2^{n-1}$個存在)の間に辺を引く。
その後、元々 $b$ に属していた頂点全ての番号を $2^{n-1}$ だけ増やす。
順列化$n$次元ハイパーキューブを、以下のように構成されるグラフと定義します。
1. $n$次元ハイパーキューブと、$0$~$2^n-1$ までの整数が1つずつ含まれる長さ$2^n$ の順列 $P$ を用意する。($P$は0-indexed)
2. $n$ 次元ハイパーキューブの番号 $i$ の頂点に、$P_i$ をメモする。
3. 各頂点の番号を2.でメモした数に置き換える。
以下に、3次元ハイパーキューブ(左)と、順列化3次元ハイパーキューブ(右)の例を示します。

順列化$n$次元ハイパーキューブには、以下のような特性があることに注意してください。
・ ちょうど $2^n$ 個の頂点を持つ。
・ ちょうど $n \times 2^{n-1}$ 本の辺を持つ。
・ それぞれの頂点は、ちょうど $n$ 個の他の頂点と辺で接続されている。
・ 自己辺や、多重辺を含まない無向グラフである。
順列化$n$次元ハイパーキューブの辺の情報が与えられます。この順列化ハイパーキューブを、上記の定義に従って、$n$次元ハイパーキューブから構成する際に使用する順列 $P$ を求めてください。
また、あなたは $0$~$n-1$ までの番号が付けられた $n$ 個の相異なる色を持っています。あなたは、与えられた順列化$n$次元ハイパーキューブの各頂点をいずれか1つの色で塗りたいです。この時、以下の条件を満たす塗り方を一つ見つけてください。
・全ての頂点に関して、その頂点から辺で接続された $n$ 個の頂点に、 色$0$~$n-1$ までの各色が1つずつ塗られている。
$n$ 次元ハイパーキューブの辺の情報が与えられるので、順列$P$ と色の塗り方をそれぞれ1つずつ見つけてください。複数個ある場合は、いずれを答えても正解となります。
#### ●入力
1行目に、テストケースの個数を表す整数 $t(1 \le t \le 4096)$ が与えられます。
それぞれのテストケースにおいて、まず1行目に順列化ハイパーキューブの次元数を表す整数 $n(1 \le n \le 16)$ が与えられます。
続く $n \times 2^{n-1}$ 行には、2つの整数 $u\ v(0 \le u,v < 2^n)$ が与えられる。これは、順列化ハイパーキューブの辺の両端にある頂点番号を指しています。
与えられる入力は、順列化$n$次元ハイパーキューブであることが保証されます。
さらに、全てのテストケースにおける $2^n$ の総和は $2^{16} = 65536$ を超えないことが保証されます。
#### ●出力
各テストケース2行出力してください。
1行目には、長さ $2^n$ の順列 $P$ を出力します。2つのハイパーキューブは、辺集合が等しい場合に同じであるとみなされることに注意してください。
2行目には、色の塗り方を出力します。まず、条件を満たす塗り方が存在しない場合、`-1` を出力します。
そうでない場合、$2^n$ 個の整数を出力してください。$i$ 番目(0-indexed)には、順列化ハイパーキューブの番号$i$ の頂点に塗る色 $c_i(0\le c_i < n)$ を出力してください。
答が複数種類ある場合は、いずれを出力しても正解となります。
#### ●入出力例
##### 入力例1
```
3
1
0 1
2
0 1
1 2
2 3
3 0
3
0 1
0 5
0 7
1 2
1 4
2 5
2 6
3 5
3 6
3 7
4 6
4 7
```
##### 出力例1
```
0 1
0 0
0 1 3 2
0 0 1 1
5 3 0 7 2 6 1 4
-1
```
最初のケースにおける色の塗り方は以下のようになります。

2個目のケースにおける色の塗り方は以下のようになります。

3個目のケースにおける順列化ハイパーキューブは、問題文中の画像で与えられたものと同一です。$P$ は出力例で示したもの以外にも、
$[0,5,7,3,1,2,4,6]$
$[0,1,5,2,7,4,3,6]$
などが条件を満たします。なお、色の塗り方は存在しないことが示せます。
## ◎ヒント・解説
### ヒント・解説に関しての諸注意
各問題のポイントをヒントという形で紹介しています。
コンテスト中であっても、詰まってしまったらぜひご確認ください。
コンテスト後に復習する際に活用していただいてもいいです。
序盤の問題に関しては一部実装をpython,C++で紹介しています.
pythonに関して, Codeforcesでは以下の5つの実行環境を利用できます.
・python 2.7.18
・python 3.8.10
・PyPy 2.7.13 (7.3.0)
・PyPy 3.6.9 (7.3.0)
・PyPy 3.7.10 (7.3.5, 64bit)
ヒントは、PyPy3.6.9 (7.3.0) もしくは PyPy 3.7.10 (7.3.5, 64bit) を利用することを前提に書いています. なお, Codeforcesのpython環境では, ASCIIに含まれない文字を含んだコードを提出するとエラーになることがありますので注意してください.
C++に関しては、以下のヘッダが記述されていることを前提にしています. ご注意ください.
```cpp=
#include <bits/stdc++.h>
using namespace std;
```
### ◎A. Repeating Cipher
:::spoiler **ヒント1**
制約($t$の長さ)が小さいので、やや無理やりな方法でも正解できます。
:::
:::spoiler **ヒント2**
無理やりな方法として、 $s$ の長さは10以下のため、$t$の長さも10通りしかありません。
これを利用し、$t$の長さで場合分けしてしまう方法があります。
:::
:::spoiler **ヒント3(文字列の扱い方に関するヒント)**
ここでは、実装で詰まりそうなポイントをヒントの形で紹介します。
文字列の $i$ 文字目を抜き出すのは、以下のように書けます。($i$ = 2 の場合を紹介)
```python=
#python
t = "abcdef"
print (t[2]) #"c"が出力されます
```
```cpp=
//C++
string t = "abcdef";
cout << t[2] << '\n'; //"c"が出力されます
```
また、言語によっては文字列に足し算が用意されていることがあります。
これを使うことで、文字列の後ろに文字をどんどん足していく、といったことが実装できます。
以下はその例です。
```python=
#python
t = "abc"
t = t + "x" + t
print (t) #"abcxabc"が出力されます
```
```cpp=
//C++
string t = "abc";
t = t + "x" + t;
cout << t << '\n'; //"abcxabc"が出力されます
```
:::
:::spoiler **解説1**
無理やりな方法をより具体的に考えてみます。
$s$が1文字の場合を考えてみましょう。$s$ = "a" のとき、
$t$ = "a" となります。逆に考えると$t$が1文字の時、 $t$の1文字目を出力すれば答えになります。
$s$が2文字で $s$ = "ab" の時、 $t$ = "abb" となります。
逆に考えると$t$が3文字の時、 $t_0t_1$ を出力すれば答えになります。($t_i$ は 0-indexedで $t$ の $i$ 文字目という意味です。)
$s$が3文字で $s$ = "abc" の時、 $t$ = "abbccc" となります。
逆に考えると$t$が6文字の時、 $t_0t_1t_3$ を出力すれば答えになります。
$s$が4文字で $s$ = "abcd" の時、 $t$ = "abbcccdddd" となります。
逆に考えると$t$が10文字の時、 $t_0t_1t_3t_6$ を出力すれば答えになります。
$s$が5文字で $s$ = "abcde" の時、 $t$ = "abbcccddddeeeee" となります。
逆に考えると$t$が15文字の時、 $t_0t_1t_3t_6t_{10}$ を出力すれば答えになります。
さて、この調子で $s$ が10文字目まで場合分けを書くことで正解できます。
しかし、これはかなり面倒です。次の項からはよりスマートに書く方法を考えます。
:::
:::spoiler **解説2**
ヒント3で、$s$が3文字・4文字・5文字の場合に注目してみます。
$s$ が3文字の場合、$t$ は6文字で、$t_0t_1t_3$ を出力すれば答えになります。
$s$ が4文字の場合、$t$ は10文字で、$t_0t_1t_3t_6$ を出力すれば答えになります。
$s$ が5文字の場合、$t$ は15文字で、$t_0t_1t_3t_6t_{10}$ を出力すれば答えになります。
さて、しっかりと観察すると規則性が見えてきます。
$s$が3文字から4文字になった時は、$s$が3文字の時に取らなければいけない$t_0t_1t_3$ に加えて1文字 $t_6$ を追加で取る必要があります。
$s$が4文字から5文字になった時は、$s$が4文字の時に取らなければいけない$t_0t_1t_3t_6$ に加えて1文字 $t_{10}$ を追加で取る必要があります。
つまり、取らなければいけない箇所は1文字少ない場合と比較すると、その大部分が共通しています。
この性質を利用すると、以下のように少しスマートに書くことができます。
0. 変数を $ans$ = "" で初期化しておく。
1. $t_0$ が存在するのなら、$ans$の後ろに $t_0$ を付けたす。
2. $t_1$ が存在するのなら、$ans$の後ろに $t_1$ を付けたす。
3. $t_3$ が存在するのなら、$ans$の後ろに $t_3$ を付けたす。
4. $t_6$ が存在するのなら、$ans$の後ろに $t_6$ を付けたす。
5. $t_{10}$ が存在するのなら、$ans$の後ろに $t_{10}$ を付けたす。
6. ...
7. ...
8. ...
9. ...
10. $t_{45}$ が存在するのなら、$ans$の後ろに $t_{45}$ を付けたす。
これで少しはスマートになりました。
if文を10個書くのもいいですが、index(0,1,3,6,...,45) を配列に入れておき、for文で回すことでさらにスマートに書けます。
これを実装したのが、以下の実装例です。
:::
:::spoiler **解説2の実装例 (python/C++)**
```python=
# python
n = int(input())
t = input()
ans = ""
idx = [0,1,3,6,10,15,21,28,36,45]
for i in idx:
if i < n:
ans += t[i]
print (ans)
```
```cpp=
//C++
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
string t;
cin >> t;
string ans = "";
vector<int> idx = {0,1,3,6,10,15,21,28,36,45};
for (int i : idx){
if (i < n) ans += t[i];
}
cout << ans << '\n';
}
```
:::
:::spoiler **解説3**
さて、上の解答例では $idx$ を全て手計算した後にコード中に書いていました。
今回は制約が小さいためこのような方法が取れましたが、制約が大きくなるとこの方法では厳しくなります。
この項では
$idx = [0,1,3,6,10,15,21,28,36,45]$
を、ループを利用して導出する方法を考えます。
$idx$ の $i$ 項目(0-indexed) は、 $0$ から $i$ までの和になっています。
これは、等差数列の和の公式を利用することで高速に計算できます。($i$項目は、初項0、公差1、項数$i+1$ の等差数列の和を求めればよいです)
また、$i-1$ 項目の結果に、$i$ を足すのを繰り返すことでも実現できます。
:::
:::spoiler **解説3の実装例(1) (python/C++)**
ここでは、等差数列の和の公式を利用して、idxを計算する実装を紹介します。
```python=
# python
n = int(input())
t = input()
ans = ""
idx = []
for i in range(10):
idx.append( (0+i)*(i+1)//2 ) #等差数列の和の公式
for i in idx:
if i < n:
ans += t[i]
print (ans)
```
```cpp=
//C++
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
string t;
cin >> t;
string ans = "";
vector<int> idx;
for (int i = 0 ; i < 10 ; ++i){
idx.push_back( (0+i)*(i+1)/2 );
}
for (int i : idx){
if (i < n) ans += t[i];
}
cout << ans << '\n';
}
```
:::
:::spoiler **解説3の実装例(2) (python/C++)**
ここでは、 $i-1$ 項目に $i$ を加えるのを繰り返す手法について紹介します。
```python=
# python
n = int(input())
t = input()
ans = ""
idx = [0]
for i in range(1,10):
idx.append( idx[-1] + i )
for i in idx:
if i < n:
ans += t[i]
print (ans)
```
```cpp=
//C++
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
string t;
cin >> t;
string ans = "";
vector<int> idx = {0};
for (int i = 1 ; i < 10 ; ++i){
idx.push_back( idx[i-1] + i );
}
for (int i : idx){
if (i < n) ans += t[i];
}
cout << ans << '\n';
}
```
:::
### ◎B. Array Stabilization
:::spoiler **ヒント1**
どのような要素を削除すると不安定さは変わるでしょうか。
:::
:::spoiler **ヒント1に対する答え**
最小値か最大値を削除したときに不安定さは変化する可能性があります。
:::
:::spoiler **ヒント2**
そのような要素を削除したあとの不安定さは、どのようにして計算できるでしょうか。
:::
:::spoiler **ヒント2に対する答え**
2番目に小さい値と、2番目に大きい値がわかれば計算できます。
:::
:::spoiler **ヒント3(実装方針)**
入力を受け取ったあと、昇順にソートすると○番目に小さい(大きい)数がすぐにわかります。
PythonとC++では、次のようにすると入力を受け取ってソートができます。
```python=
n = int(input())
a = list(map(int, input().split()))
a.sort()
```
```cpp=
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
sort(a.begin(), a.end());
}
```
:::
:::spoiler **解説1**
削除する要素の候補は最小値と最大値の2つあるので、2通りについて不安定さを計算して小さい方が答えになります。
小さい方は、`min` を利用するとPython/C++では求められます。
例えば、次のようにすると $a, b$ の小さい方を出力します。
```python=
print(min(a, b))
```
```cpp=
cout << min(a, b) << endl;
```
:::
:::spoiler **解説2**
2通りについての不安定さは、ソート済みの $a$ に対してそれぞれ次のように計算できます。
- 最小値を削除するとき
- `a[n - 1] - a[1]`
- `a[n - 1]`が1番大きい要素で、`a[1]` が2番目に小さい要素
- 最大値を削除するとき
- `a[n - 2] - a[0]`
:::
:::spoiler **実装例のまとめ(C++/Python)**
ここまでのヒントと解説をまとめると、次のようなコードになります。
```python=
n = int(input())
a = list(map(int, input().split()))
a.sort()
print(min(a[n - 2] - a[0], a[n - 1] - a[1]))
```
```cpp=
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
sort(a.begin(), a.end());
cout << min(a[n - 2] - a[0], a[n - 1] - a[1]) << endl;
}
```
:::
### ◎C. Powers Of Two
:::spoiler **ヒント1**
$n$ を `power of two` の和に分割するにあたり、分割できる個数の最大値・最小値を考えましょう。
:::
:::spoiler **ヒント2**
最大値は簡単です。1は `power of two` であるため、1が$n$ 個にすることで、分割個数の最大値 $n$ が達成できます。
:::
:::spoiler **ヒント3**
最小値を考えるにあたって、$n$ を2進数で表してみましょう。
:::
:::spoiler **ヒント4**
2進数で表したとき、立っているビットの数が最小値です。
立っているbitに対応する `power of two` の和として表せばよいです。
例:
n = 14 の時、2進数表記は 1110 なので分割個数の最小は3つです。
2,4,8 の桁のビットが立っているため、 14 = 2+4+8 と分解できます。
:::
:::spoiler **ヒント5**
最大値と最小値が分かれば、その間に $k$ が含まれていない場合には `NO` です。
そしてこの問題では、含まれている場合は常に `YES` となることが示せます。
:::
:::spoiler **ヒント6**
1以外の `power of two` は全て2つの `power of two` に分解できます。
例: 16 = 8 + 8
:::
:::spoiler **解説**
まず、$n$ を最小個数の `power of two` に分解します。
分解にあたってまず、`power of two` を$1,2,4,8,16,32,...$ というように列挙しておきます($n$を超えるまで)。
また、空の配列 $minpot$ を用意します。
`power of two` を大きいほうから見ていき、現在見ている値 $pot$ が、 $n$ 以下の場合は $n$ から $pot$ を引き、$minpot$ に $pot$ をpushします。
これを繰り返すことで、最終的に $minpot$ が最小個数の分割となります。
最大個数の分割は、 $n$ であることが分かっているので、 $k$ が $|minpot|$ 以上 $n$ 以下でない場合、`NO` を出力します。
そうでない場合、 `YES` を出力し、具体的な分割の構成を行います。
具体的な分割を構成するにあたって、まず $minpot$ を $notone$ と $one$ の2つの配列に分割します。
$notone$ には、1ではない値を入れ、$one$ には1を入れます。
そして、$|notone| + |one| = k$ となるまで、以下の操作を繰り返します。
この操作を行うたびに、$|notone| + |one|$ は1ずつ増えることから、いずれ $k$ に達することが分かります。
1. notone から1つ要素 $p$ を取ってきて、削除する。(pythonのリストやC++のvectorにおいては、一番後ろの要素を削除するとO(1)で高速です。)
2. $p$ が 2 の場合、 $one$ に 1 を2個pushする。そうでない場合、$notone$ に $\frac{p}{2}$ を2個pushする。
$|notone| + |one| = k$ となったら、 $notone$ と $one$ を結合したものが具体的な分割となっています。
:::
:::spoiler **実装例(python)**
上の解説に従った実装例です。
```python=
#python
import sys
from sys import stdin
n,k = map(int,stdin.readline().split())
power_of_two = []
for i in range(30,-1,-1):
power_of_two.append(2**i)
minpot = []
tmpn = n
for pot in power_of_two:
if pot <= tmpn:
tmpn -= pot
minpot.append(pot)
notone = []
one = []
for i in minpot:
if i == 1:
one.append(i)
else:
notone.append(i)
if len(notone) + len(one) > k or k > n:
print ("NO")
sys.exit()
while len(notone) + len(one) != k:
last = notone[-1]
del notone[-1]
if last == 2:
one.append(1)
one.append(1)
else:
notone.append(last//2)
notone.append(last//2)
ans = notone + one
print ("YES")
print (" ".join(map(str,ans)))
```
:::
### ◎D. Circular Dance
:::spoiler **ヒント1**
子ども $i$ の前にいる2人は $a_{i, 1}$ と $a_{i, 2}$ で、この2人のどちらが前かはわかりませんが連続しています。
この2人の順番を特定できないでしょうか。
:::
:::spoiler **ヒント2**
$x = a_{i, 1}$ の前に $y = a_{i, 2}$ がいるとします。
このとき、$a_{x, 1}, a_{x, 2}$ はどのようになるでしょうか。
:::
:::spoiler **ヒント3**
実装方針によっては $n = 3$ がコーナーケースになります。
:::
:::spoiler **解説**
すべての子ども $i$ について、$x_i = a_{i, 1}, y_i = a_{i, 2}$ とします。
ここで、$a_{x_i, 1} = y_i$ もしくは $a_{x_i, 2} = y_i$ であれば子ども $x_i$ の前に $y_i$ がいて、そうでなければ子ども $y_i$ の前に $x_i$ がいます。
ただし、$n=3$ の場合にはどちらの条件も満たすので、子ども2と子ども3の両方の目の前に子ども1がいることになってしまうことがあります。
$n=3$ ではどのような順列も条件を満たすので、先に適当な順列を出力しておきましょう。
このようにすることで、各子どもの目の前にいる子どもが特定できます。
その後は、子ども1から始めて目の前にいる子どもを辿りながら出力していけばよいです。
:::
### ◎E. Almost Regular Bracket Sequence
:::spoiler **ヒント1**
括弧列の問題は、'(' を +1 , ')' を -1 とみなすことで解きやすくなることがあります。
:::
:::spoiler **ヒント2**
標準括弧列である条件を考えます。
ヒント1での置き換えを行った後、$b_i$ = $s_1 + s_2 + ... + s_i$ であるような長さ $n$ の数列 $b$ を考えます。
$b$ の最小値が $0$ かつ、 $b_n = 0$ であることが、標準括弧列である必要十分条件です。
:::
:::spoiler **ヒント3**
$i$項目の '(' → ')' の置き換えは、$b$ の $i$ 項目以降を全て 2だけ減少させます。
$i$項目の ')' → '(' の置き換えは、$b$ の $i$ 項目以降を全て 2だけ増加させます。
:::
:::spoiler **解説**
各 $i$ について、置き換えを行ったときにヒント2の条件を満たしているかを調べればよいです。
各 $i$ について、$b$ の先頭から $i-1$ 項の最小値と、$i$ 項目以降の最小値が分かればよいため、これらを事前計算しておくことで解けます。
具体的には、$i$項目の '(' → ')' の置き換えの際は、$b_n = 2$ かつ、 $b_i$ 以降の最小値が2、$b_{i-1}$ 以前の最小値が0以上なら可。
$i$項目の ')' → '(' の置き換えの際は、$b_n = -2$ かつ、 $b_i$ 以降の最小値が-2、$b_{i-1}$ 以前の最小値が0以上なら可。
ミスが怖い場合、区間加算・区間最小値取得の遅延評価セグメント木を使用することで愚直に実装できます。
:::
### ◎F. Make It Connected
:::spoiler **ヒント1**
辺のコストの和が最小になるように選び、連結にしたいという問題です。
:::
:::spoiler **ヒント2**
最小全域木を求める問題になりますが、辺の数が $O(n^2 + m)$ なのでそのままでは Kruskal 法が使えません。
:::
:::spoiler **ヒント3**
使われる可能性がある辺は $o(n^2)$ にならないでしょうか。
:::
:::spoiler **ヒント4**
特別なオファーがない場合を考えてみましょう。
:::
:::spoiler **解説**
$a_i$ が最小の $i (=: v)$ を一つ見つけたとき、頂点 $v$ と他の頂点を結ぶ辺と特別なオファーしか最終的に使いません。
特別なオファーがないとき、$v$ とその他の頂点をすべて結ぶのが最適になります。
Kruskal法を適用していく過程を考えます。このとき、2つの連結成分を結ぶ辺を追加するときには、各連結成分の中で $a_i$ が最小の頂点を結ぶことになります。ここで、どちらかは頂点 $v$ です。
仮にどちらも $v$ ではなく頂点 $x, y (a_x \leq a_y)$ であったとすると$a_x + a_y < a_v + a_x$ ということになりますが、これは $a_v$ が最小であることに矛盾します。$a_y = a_v$ のときには、$a_v$ を優先するとしても問題ないです。
よって、特別なオファー以外から使う辺は $(i, v) (i \neq v)$ だけを考えればよいため辺の数は $O(n + m)$ になりました。
後は、この辺集合に対してKruskal法を適用することで解けます。
:::
### ◎G. The Final Pursuit
面白い問題です。
スライドに簡単な解説が載せてあります。
また、公式解説がヒント・解説の両方が非常に充実しているのでこちらをどうぞ
https://codeforces.com/blog/entry/92582
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet