# 競プロ講習会第14回 Web資料
## ◎第14回の参加方法について
今回も、好きな時間に問題を解いておくことができるようにします。
講習会開始後30分は問題を解く時間に充てますが、ちゃんと時間を取って解きたい人は以下の方法で事前に参加してください。
まず、Codeforcesにログインします。
その後、K-LMSに公開してあるコンテストリンクを開きます。
KeioAICKyoproCourseContest #14 に、**Virtual participation**します。**Enter**の方ではないので注意!!!
(※Virtual perticipation機能は、好きな時間を選んでコンテストに参加できる機能です. Enterを押して入ると、コンテスト外で問題を解いたことになります。)
開始したい時間を入力し、Registar for virtual participationを押します。
指定した時間になったらコンテストが始まるので、問題を解きます。
コンテストの時間終了後、講習会前であっても解き直しなど自由に行っていただいて構いません。
また、参加中であってもweb資料のヒント・解説は参照してかまいません。
Slackの公開チャンネルやDMでの質問も受け付けますのでお気軽にどうぞ(すぐに答えられるとは限りませんがご了承ください)。
#### ◎問題セット
https://codeforces.com/contestInvitation/af3e9520c3771fbf07fa69df495800fa82231ded
#### ◎公式解説
##### A〜F問題
https://codeforces.com/blog/entry/64751
## ◎問題訳(意訳あり注意)
### ◎A. Two distinct points
:::spoiler **クリックで展開**
TL: 1s ML: 256MB
#### ●問題
あなたは、2つの区間 $[l_1;r_1] , [l_2;r_2]$ を貰いました。$l_1 < r_1 , l_2 < r_2$ であることが保証されています。
2つの区間は、交叉したり、片方が他方に完全に含まれる可能性があります。

$l_1 \le a \le r_1 , l_2 \le b \le r_2 , a \neq b$ であるような整数 $a,b$ を見つけてください。言い換えると、1つ目の区間$[l_1;r_1]$に含まれる点 $a$ と、2つ目の区間$[l_2;r_2]$に含まれる点 $b$ のペアの中で、$a,b$ が相異なるものを一つ見つけてください。
答えは必ず存在することが証明できます。答えが複数存在する場合は、どれを出力しても構いません。
以上の問題が $q$ 個与えられるので、それぞれについて答えを求めてください。
#### ●入力
1行目に、与えられる問題(クエリ)の数 $q (1 \le q \le 500)$ が与えられます。
続く $q$ 行の各行に、1つのクエリの入力である4つの整数 $l_1,r_1,l_2,r_2 (1 \le l_1,r_1,l_2,r_2 \le 10^9 , l_1 < r_1 , l_2 < r_2)$ が与えられます。これは、問題文中の区間の端を表しています。
#### ●出力
$q$ 行出力してください。
各行には、$l_1 \le a \le r_1 , l_2 \le b \le r_2 , a \neq b$ であるような整数 $a,b$ を空白区切りで出力してください。
答が存在しうることは証明でき、複数答がある場合はどれを出力しても構いません。
#### ●入出力例
##### 入力例1
```
5
1 2 1 2
2 6 3 4
2 4 1 3
1 2 1 3
1 4 5 8
```
##### 出力例1
```
2 1
3 4
3 2
1 2
3 7
```
:::
### ◎B. Divisors of Two Integers
:::spoiler **クリックで展開**
TL: 1s ML: 256MB
#### ●問題
あなたは、最近2つの整数 $x,y$ を見つけましたが、それを忘れてしまいました。しかし、あなたは代わりに $x,y$ の全ての約数をシャッフルしたリストを持っています。より厳密には、$x$ の全ての約数を列挙した数列と、$y$ の全ての約数を列挙した数列を繋ぎ合わせ、任意の順番にシャッフルすることによって生成された数列を持っています。ある数が $x,y$ の公約数の場合、その数はリストに2回登場することになります。
例えば、 $x=4,y=6$ の場合、$a = [1,2,4,1,2,3,6]$ を任意の順番にシャッフルした数列が与えられます。$[1,1,2,4,6,3,2], [4,6,1,1,2,3,2],[1,6,3,2,4,1,2]$ などがこれに該当します。$a$ 自身も該当します。
与えられたリストから、$x,y$ を復元してください。なお、出力の際に $x,y$ の順序は問いません。
答えが存在するような入力のみ与えられます。
#### ●入力
最初の行に、整数 $n (2 \le n \le 128)$ が与えられます。これは、リストに含まれる要素の個数です。
2行目に、$n$ 個の整数 $d_1,d_2, ... , d_n (1 \le d_i \le 10^4)$ が与えられます。
#### ●出力
考えられる2整数 $x,y$ を空白区切りで出力してください。
$x,y$ の順序は問いません。また、答が存在することは保証されます。
#### ●入出力例
##### 入力例1
```
10
10 2 8 1 2 4 1 20 4 5
```
##### 出力例1
```
20 8
```
:::
### ◎C. Nice Garland
:::spoiler **クリックで展開**
TL: 1s ML: 256MB
#### ●問題
あなたは $n$ 個のランプからなる装飾を持っていて、それぞれのランプは赤、緑、青に光っています。 $i$ 番目のランプの最初の色は $s_i$ (`'R', 'G', 'B'`) です。
あなたは、garland のランプの内いくつかの色を変えて、装飾を **nice** にする必要があります。
装飾にある同じ色のランプ全てのペアの距離が 3 で割り切れるとき、**nice** であるといいます。つまり、garland $t$ について、任意の $i, j$ で $t_i = t_j$ であれば、 $|i - j| \mod 3 \equiv 0$ です。 $|x|$ は $x$ の絶対値で、 $x \mod y$ は $x$ を $y$ で割ったあまりです。
例えば、`"RGBRGBRG", "GB", "R", "GRBGRBG", "BRGBRGB"` は **nice** で、`"RR", "RGBG"` は **nice** ではありません。
装飾を **nice** にするすべての色の変え方の中で、最も色が変わったランプの数が **少ない** ものを出力してください。複数答えがある場合はいずれを出力しても構いません。
#### ●入力
最初の行に、整数 $n(1 \leq n \leq 2 \cdot 10^5)$ として、ランプの個数が与えられます。
2行目に、$n$ 文字の `'R', 'G', 'B'` からなる文字列 $s$ として、装飾のランプの色が与えられます。
#### ●出力
最初の行に、1つの整数 $r$ として、装飾を **nice** にするために色を変える必要があるランプの個数として **最小** の個数を答えてください。
2行目に、長さ $n$ の文字列 $t$ として、$r$ 個のランプの色を変えることで得られた **nice** な装飾を出力してください。複数の最適解が存在する場合、任意のものを出力しても大丈夫です。
#### ●入出力例
##### 入力例1
```
3
BRB
```
##### 出力例1
```
1
GRB
```
##### 入力例2
```
7
RGBGRBB
```
##### 出力例2
```
3
RGBRGBR
```
:::
### ◎D. Diverse Garland
:::spoiler **クリックで展開**
TL: 1s ML: 256MB
#### ●問題
あなたは $n$ 個のランプからなる装飾を持っています。各ランプは赤、緑、青に光っていて、$i$ 番目のランプの色は $s_i$ (`'R, 'G', 'B'`) で与えられます。
あなたは、装飾に含まれるいくつかのランプの色を変えることで、 **diverse** な装飾にしたいです。
2つの隣り合ったランプ (距離が 1 であるもの) 全てのペアについて、色が異なるときに **diverse** な装飾であるといいます。
言い換えると、**diverse** な装飾 $t$ は、全ての $1$ から $n-1$ までの $i$ について $t_i \neq t_{i + 1}$ を満たしています。
装飾を **diverse** にするために色を変える全ての方法の中で、色が変わったランプの個数を **最小** にするものを見つけてください。最適な答えが複数ある場合には、いずれを出力しても構いません。
#### ●入力
最初の行に、1つの整数 $n(1 \leq n \leq 2 \cdot 10^5)$ として、ランプの個数が与えられます。
2行目に、$n$ 文字の `'R', 'G', 'B'` からなる文字列 $s$ として、装飾のランプの色が与えられます。
#### ●出力
最初の行に、1つの整数 $r$ として、装飾を **diverse** にするために色を変える必要があるランプの個数として **最小** の個数を答えてください。
2行目に、長さ $n$ の文字列 $t$ として、$r$ 個のランプの色を変えることで得られた **diverse** な装飾を出力してください。複数の最適解が存在する場合、任意のものを出力しても大丈夫です。
#### ●入出力例
##### 入力例1
```
9
RBGRRBRGG
```
##### 出力例1
```
2
RBGRGBRGR
```
##### 入力例2
```
8
BBBGBRRR
```
##### 出力例2
```
2
BRBGBRGR
```
##### 入力例3
```
13
BBRRRRGGGGGRR
```
##### 出力例3
```
6
BGRBRBGBGBGRG
```
:::
### ◎E. Array and Segments
:::spoiler **クリックで展開**
TL: 2s ML: 256MB
**E1 と E2 の違いは入力のサイズのみなのでまとめてあります。「入力」の部分で違いを示しています。**
#### ●問題
$n$ 要素からなる数列 $a$ があります。$i$ 番目の要素は $a_i$ です。
また、$m$ 個の区間があります。 $j$ 番目の区間は、$[l_j;r_j]$ であり、$1 \le l_j \le r_j \le n$ を満たします。
あなたは、$m$ この区間のうち、いくつか(全部や0個でも構わない)を選びます。そして、選んだ各区間 $[l_j,r_j]$ に対して1回ずつ、以下の操作を行います。
・$l_j \le i \le r_j$ を満たすような全ての整数 $i$ について、 $a_i$ から1を引く。
全ての操作が終了したときの $a$ を $b$ と呼ぶことにします。
例えば、$a = [0,0,0,0,0]$ で、$[1;3],[2;4]$ の2つの区間を選んだ場合、操作後の列 $b$ は $b = [-1,-2,-2,-1,0]$ となります。
$d = bの最大の要素-bの最小の要素$ とします。
あなたは、与えられた区間の集合から適切に区間の集合を選ぶことにより、$d$ を最大化したいです。
$d$ の最大値と、これを達成するときの適切な区間の選び方を求めてください。
区間は1つも選ばなくてもよく、答が複数ある場合どれを出力しても構いません。
pythonを利用している人は、Pypyを使用するのを推奨します。
#### ●入力
##### **E1**
1行目に2つの整数 $n,m (1 \le n \le 300,0 \le m \le 300)$ が与えられます。$n$ は $a$ の要素の数、$m$ は与えられる区間の数です。
2行目に、$n$ 個の整数 $a_1,a_2, ... , a_n (-10^6 \le a_i \le 10^6)$ が与えられます。
続く $m$ 行に、区間の端である $l_j,r_j (1 \le l_j \le r_j \le n)$ が与えられます。
##### **E2**
1行目に2つの整数 $n,m (1 \le n \le 10^5,0 \le m \le 300)$ が与えられます。$n$ は $a$ の要素の数、$m$ は与えられる区間の数です。
2行目に、$n$ 個の整数 $a_1,a_2, ... , a_n (-10^6 \le a_i \le 10^6)$ が与えられます。
続く $m$ 行に、区間の端である $l_j,r_j (1 \le l_j \le r_j \le n)$ が与えられます。
#### ●出力
1行目に、$d$ として考えられる最大値を出力してください。
2行目に、それを達成するために選ぶべき区間の個数 $q (0 \le q \le m)$ を出力します。
3行目には、$d$ の最大値を達成するために選ぶべき区間の番号 $c_1,c_2, ... ,c_q (1 \le c_k \le m)$ を空白区切りで出力してください。
答が複数通りある場合、どれを出力しても構いません。
#### ●入出力例
##### 入力例1
```
5 4
2 -2 3 1 2
1 3
4 5
2 5
1 3
```
##### 出力例1
```
6
2
4 1
```
$b = [0,-4,1,1,2]$ となり、$d = 6$ です。
##### 入力例2
```
5 4
2 -2 3 1 4
3 5
3 4
2 4
2 5
```
##### 出力例2
```
7
2
3 2
```
$b = [2,-3,1,-1,4]$ となり、$d = 7$ です。
##### 入力例3
```
1 0
1000000
```
##### 出力例3
```
0
0
```
何もする必要はなく、答えは0です。
:::
### ◎F. MST Unification
:::spoiler **クリックで展開**
TL: 1s ML: 256MB
#### ●問題
$n$ 頂点 $m$ 辺からなる、**自己ループと多重辺のない連結な** 重み付き無向グラフが与えられます。
$i$ 番目の辺は $e_i = (u_i, v_i, w_i)$ として与えられ、頂点 $u_i, v_i$ を重み $w_i$ の辺 $e_i$ が結んでいることを意味します。グラフは連結なので、任意の頂点のペアについて、与えられたグラフの辺のみを用いたパスが少なくとも1つ存在します。
重みが正の場合の最小全域木 (MST) は、連結無向グラフの辺の部分集合であってすべての頂点を連結にするもののうち重みの和が最小のものです。
あなたは適当な辺の重みを 1 増やすことで与えられたグラフを修正することができます。この操作は、好きなだけ繰り返すことができます。
最初のグラフにおける最小全域木のコストを $k$ としたとき、あなたが解くべき問題は、**最小の操作回数で** いくつかの辺の重みを増やして最小全域木のコストは $k$ のまま **unique** にすることです。**unique** とは、操作後のグラフについて最小全域木が一種類しかないことを指します。
目標を達成するために必要な **最小の** 操作回数を計算してください。
#### ●入力
最初の行に、2つの整数 $n, m\, (1 \leq n \leq 2 \cdot 10^5, n-1 \leq m \leq 2 \cdot 10^5)$ として、最初のグラフにおける頂点数と辺の数がそれぞれ与えられます。
続く $m$ 行にはそれぞれ 3 つの整数が含まれていて、$i$ 番目の行は辺 $e_i$ の情報になっています。3つの整数はそれぞれ、 $u_i, v_i, w_i (1 \leq u_i, v_i \leq n, u_i \neq v_i, 1\leq w \leq 10^9)$ で、$u_i$ と $v_i$ を結ぶ重み $w_i$ の辺であることを意味しています。
与えられたグラフに自己ループと多重辺が存在しないことが保証されます (任意の $i (1 \leq i \leq m)$ について $u_i \neq v_i$ であり、順番のない頂点のペアとして $(u, v)$ は辺が結ぶ頂点対として高々1回しか登場しない) 。
また、与えられたグラフが連結であることも保証されます。
#### ●出力
1つの整数として、最初のグラフの最小全域木のコストを変えずに **unique** にするための操作回数として **最小** のものを出力してください。
#### ●入出力例
##### 入力例1
```
8 10
1 2 1
2 3 2
2 4 5
1 4 2
6 3 3
6 1 3
3 5 2
3 7 1
4 8 1
6 2 4
```
##### 出力例1
```
1
```
図示すると次のようになります。
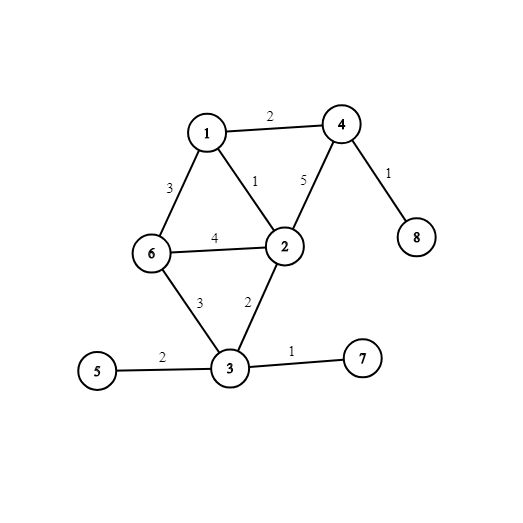
例えば、辺 $(1, 6)$ か $(6, 3)$ の重みを 1 増やすと最小全域木を唯一にできます。
##### 入力例2
```
4 3
2 1 3
4 3 4
2 4 1
```
##### 出力例2
```
0
```
##### 入力例3
```
3 3
1 2 1
2 3 2
1 3 3
```
##### 出力例3
```
0
```
##### 入力例4
```
3 3
1 2 1
2 3 3
1 3 3
```
##### 出力例4
```
1
```
##### 入力例5
```
1 0
```
##### 出力例5
```
0
```
##### 入力例6
```
5 6
1 2 2
2 3 1
4 5 3
2 4 2
1 4 2
1 5 3
```
##### 出力例6
```
2
```
図示したものが次の画像です。
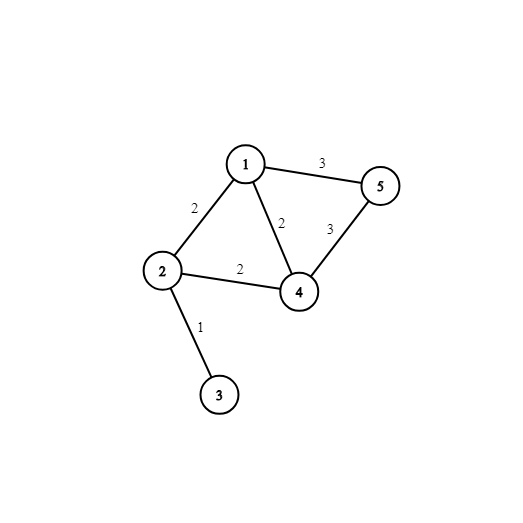
例えば、辺 $(1, 5)$ と $(2, 4)$ の重みを 1 ずつ増やすと最小全域木を唯一にできます。
:::
## ◎ヒント・解説
### ◎A. Two distinct points
:::spoiler **◎ヒント1(入力の受け取り方)**
まず、クエリの数 $q$ を受け取り、ループの中で各クエリについて答えていくとよいです。
```python=
# python
q = int(input())
for loop in range(q):
l1,r1,l2,r2 = map(int,input().split())
# ここに処理を書く
```
```cpp=
// c++
#include <bits/stdc++.h>
using namespace std;
int main() {
int q;
cin >> q;
for (int loop=0 ; loop<q ; ++loop){
int l1,r1,l2,r2;
cin >> l1 >> r1 >> l2 >> r2;
//ここに、処理を書く
}
}
```
:::
:::spoiler **◎ヒント3**
$l_1 < r_1,l_2 < r_2$ なので、$a,b$ の候補はそれぞれ最低でも2つあります。
:::
:::spoiler **◎ヒント3**
$a$ は $l_1 \le a \le r_1$ を満たす範囲内で何を選んだとしてもOKです。まず、$a$ を適当に選び、その後に $b$ を選ぶことを考えましょう。
:::
:::spoiler **◎ヒント4**
$l_2,r_2$ の内、どちらかは $a$ と異なります。
:::
:::spoiler **◎解説**
$a = l_1$ とします。
もし、$a = l_2$ ならば、$b = r_2$。そうでなければ $b = l_2$ とします。
最後に、$a\ b$ を出力すればよいです。
:::
:::spoiler **◎実装例(Python)**
```python=
# python
q = int(input())
for loop in range(q):
l1,r1,l2,r2 = map(int,input().split())
a = l1
if l2 == a:
b = r2
else:
b = l2
print (a,b)
```
:::
:::spoiler **◎実装例(C++)**
```cpp=
//c++
#include <bits/stdc++.h>
using namespace std;
int main() {
int q;
cin >> q;
for (int loop=0 ; loop<q ; ++loop){
int l1,r1,l2,r2;
cin >> l1 >> r1 >> l2 >> r2;
int a = l1;
int b;
if (l2 == a) b = r2;
else b = l2;
cout << a << " " << b << '\n';
}
}
```
:::
### ◎B. Divisors of Two Integers
:::spoiler **◎ヒント1(入力の受け取り方)**
以下のように入力を受け取ります。
```python=
# Python
n = int(input())
d = list(map(int,input().split()))
# ここに続きの処理を書く
```
```cpp=
// C++
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int main() {
int n;
cin >> n;
vector<int> d(n);
for (int i=0 ; i < n ; ++i) cin >> d[i];
// ここに続きの処理を書く
}
```
:::
:::spoiler **◎ヒント2**
まず、$x,y$ の内片方はすぐに分かります。
:::
:::spoiler **◎ヒント3**
$x$ が分かれば、その約数を列挙することができます。
$d$ から、$x$ の約数のリスト由来の要素をすべて取り除けば $y$ が分かります。
:::
:::spoiler **◎ヒント4**
$d$ から、$x$ の約数のリスト由来の要素をすべて取り除く処理は、連想配列、すなわちpythonのdictや、C++のmapを利用すると効率的に実装できます。
:::
:::spoiler **◎解説**
$y \le x$ とします。
まず、$d$ の最大の要素を $x$ としてよいです。
なぜなら、$x$ の約数の内最大のものは $x$ であり、 $y$ の約数の内最大のものは $y$ なので、$y \le x$ の条件下において $d$ に含まれる最大の要素は必ず $x$ になるからです。
次に、$x$ の約数を列挙します。
本問題の制約下において、$x \le 10^4$ なので1から順に約数かどうかを判定すればよいです。
より具体的には、整数 $i$ が $x$ の約数かどうかを判定するには、 $x$ を $i$ で割った余りが $0$ かどうかを判定すればよいです。
$d$ から $x$ の約数由来の要素を消去すれば、残るのは $y$ 由来の要素のみとなります。その中で最大の要素が $y$ なので、これを求めて出力すればよいです。
この操作の実装は様々な方法がありますが、連想配列を利用し、$d$ の中に含まれている各要素の個数を管理すると良いです。
詳しくは、実装例を確認してください。
:::
:::spoiler **◎実装例(python3)**
```python=
n = int(input())
d = list(map(int,input().split()))
M = {} #連想配列
for di in d: #M[di]=dの中にdiが含まれている個数 にする
if di not in M:
M[di] = 0
M[di] += 1
d.sort()
x = d[-1] #xをdの最大値にする
for i in range(1,x+1): #xの約数を求めて、取り除く
if x % i == 0: #iがxの約数ならば…
M[i] -= 1 #M[i]を減らす
y = 0
for di in M: #M[di]==1 であるようなdiの内、最大のものを求める
if M[di] == 1:
y = max(y,di)
print (x,y)
```
:::
:::spoiler **◎実装例(C++)**
```cpp=
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> d(n);
for (int i=0 ; i<n ; ++i) cin >> d[i];
map<int,int> M; // 連想配列
for (int di : d) M[di]++;
sort(d.begin(),d.end());
int x = d.back(); // dの最大値をxにする
for (int i=1 ; i <= x ; ++i){ //xの約数を列挙し、削除
if (x % i == 0) M[i]--;
}
int y = 0;
for (pair<int,int> di_cnt : M){ //残りの要素の最大値をyにする
int di = di_cnt.first;
int cnt = di_cnt.second;
if (cnt == 1) y = max(y,di);
}
cout << x << " " << y << '\n';
}
```
:::
### ◎C. Nice Garland
:::spoiler **◎ヒント1**
条件を満たす色の並びはどのようなときでしょうか。
:::
:::spoiler **◎ヒント2**
2個おきに同じ色が登場することがわかります。
:::
:::spoiler **◎ヒント3**
最初のいくつかを決めると、残りの色が全て決まります。
:::
:::spoiler **◎ヒント4**
`"RGB"` という文字列の並び替え全てに対しての処理は次のように実装できます。
```python=
import itertools
for prefix in itertools.permutations("RGB"):
# 処理をする
```
```cpp=
#include <bits/stdc++.h>
using namespace std;
int main() {
string prefix("RGB");
// ソートしておく必要がある
// 最初から prefix("BGR") としてもいい
sort(prefix.begin(), prefix.end());
do {
// 処理をする
} while (next_permutation(prefix.begin(), prefix.end()));
}
```
:::
:::spoiler **◎解説**
最初の3つの色の並びを決めると、残りはその並びを繰り返す必要があるとわかります。
なので、全部で色の並びは $3! = 6$ 通りしかないため試すことができます。
最初の3つの色を `RGB = "RGB"` みたいに決めたとき、これを繰り返すときの $i$ 番目のランプの色は `RGB[i % 3]` で求めることができます。
後は、そのように決めた色の並びと最初の色の並びで異なるところを変える必要があるのでそれを数えて最小のものを見つければよいです。
:::
:::spoiler **◎実装例(Python)**
```python=
import itertools
n = int(input())
s = input()
res_cost = n + 1 # コストは最大 n
res_pre = []
for prefix in itertools.permutations("RGB"):
cnt = 0
for i in range(n):
if prefix[i % 3] != s[i]:
cnt += 1
if res_cost > cnt:
res_cost = cnt
res_pre = prefix
ans = []
for i in range(n):
ans.append(res_pre[i % 3])
print(res_cost)
print("".join(ans))
```
:::
:::spoiler **◎実装例(C++)**
```cpp=
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
string s;
cin >> s;
string prefix("RGB");
// ソートしておく必要がある
// 最初から prefix("BGR") としてもいい
sort(prefix.begin(), prefix.end());
int res_cost = n + 1; // コストは最大 n
string res_pre = "";
do {
int cnt = 0;
for (int i = 0; i < n; i++) {
if (prefix[i % 3] != s[i]) {
cnt++;
}
}
if (cnt < res_cost) {
res_cost = cnt;
res_pre = prefix;
}
} while (next_permutation(prefix.begin(), prefix.end()));
string ans = "";
for (int i = 0; i < n; i++) {
ans += res_pre[i % 3];
}
cout << res_cost << endl;
cout << ans << endl;
}
```
:::
### ◎D. Diverse Garland
:::spoiler **◎ヒント1**
同じ色が連続していてはいけないので、その部分のランプのうちいくつかの色を変えないといけません。
:::
:::spoiler **◎ヒント2**
例えば、`"RRRRR"` と赤が5個連続していたらいくつ書き換える必要があるでしょうか。
`"RRRR"` と4個の場合はいくつになるでしょうか。
:::
:::spoiler **◎ヒント3**
`"GRRRRB"` のように、左右には異なる色のランプがある可能性があります。
その場合、色を変えたことで左右のランプと同じ色になってしまうことはないでしょうか。
:::
:::spoiler **◎解説**
ヒント2, 3 の解決をします。
まず、ヒント2については、長さが奇数のときは `"RRRRR"` であれば `"RBRBR"` のように偶数番目を別の色にすると同じ色で隣り合う部分がなくなります。
偶数であれば `"RRRR"` を `"RBRB"` のようにすればよいです。
ここで、ヒント3を考えてみましょう。
奇数の場合、連続する部分の端の色は `"R"` のまま変わっていないので大丈夫です。
しかし、偶数の場合は右端が `"B"` に変わってしまっています。なので、ヒント3の場合は `"GRBRBB"` と `"B"` が連続してしまうので駄目に見えます。
ただ、このときは右側に `"B"` があるとわかっているので、`"B"` でも `"R"`
でもない `"G"` に書き換えて `"GRGRGB"` とすることができます。
なので、左端からランプの色を見ていって、1つ前と同じ色であれば1つ前と次のランプ、どちらの色とも異なる色に変えることを繰り返していけば大丈夫です。
1つ前だけではなく、次の色も考慮して色を書き換えないといけないことを、奇数と偶数に場合分けして確認をここではしました。
`dp[i][j] := i 個目のランプまで色を決めて、その色は j であるときの最小コスト` というDPをして、復元することでも解くことができます。
:::
:::spoiler **◎実装例(python3)**
```python=
n = int(input())
s = list(input()) # 書き換えたいのでリストにする
RGB = "RGB"
cnt = 0
for i in range(1, n):
if s[i] == s[i - 1]:
for c in RGB:
if s[i - 1] != c and (i == n - 1 or s[i + 1] != c):
cnt += 1
s[i] = c
break
print(cnt)
print("".join(s))
```
:::
:::spoiler **◎実装例(C++)**
```cpp=
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
string s;
cin >> s;
int cnt = 0;
string RGB("RGB");
for (int i = 1; i < n; i++) {
if (s[i] == s[i - 1]) {
for (auto c : RGB) {
if (s[i - 1] != c && (i == n - 1 || s[i + 1] != c)) {
cnt++;
s[i] = c;
break;
}
}
}
}
cout << cnt << endl;
cout << s << endl;
}
```
:::
### ◎E1. Array and Segments (Easy version)
:::spoiler **◎ヒント1**
最大と最小の2要素のみが、$d(=bの最大値-bの最小値)$の値を決定します。
:::
:::spoiler **◎ヒント2**
$d$ は、$0 \le i,j \le n$ を満たす $(i,j)$ における $b_i-b_j$ の最大値と等しいです。
:::
:::spoiler **◎ヒント3**
$i,j$ を固定したとき、$b_i-b_j$ を最大化するような区間の選び方を考えましょう。
:::
:::spoiler **◎ヒント4**
$i$ を含む区間を取っても、$b_i-b_j$ が大きくなることはありません。
また、$i$ を含まない区間を取った時 $b_i-b_j$ が小さくなることはありません。よって、$i$ を含まない区間を全部取った時 $b_i-b_j$ は最大値となることが分かります。
:::
:::spoiler **◎ヒント5**
ヒント4において、取る区間の集合は $i$ によってのみ決定されるので、$j$ の方は同時に処理することができます。
:::
:::spoiler **◎解説**
全ての $i$ について、 $i$ を含まない区間を全て選択し、 $b$ を作成します。全ての $j$ について、 $d_{i,j} = b_i-b_j$ を計算します。
後は$d_{i,j}$ の最大値を求め、その時の $i$ を記録しておけば、区間の集合も求められます。
計算量は、$O(n^2m)$ です。
:::
### ◎E2. Array and Segments (Hard version)
:::spoiler **◎ヒント1**
E1の方針に対し、さらに高速化を試みることで $O(nm)$ を達成できます。
:::
:::spoiler **◎ヒント2**
$i$ が1つ隣にずれた時、選ぶべき区間の集合はほとんど変わらないことを利用します。
:::
:::spoiler **◎解説**
まず、以下の配列を計算します。
$dpL[i] = (r_j \le i であるような区間を全て選んだ場合の、b_0,b_1,...,b_i の最小値)$
$dpR[i] = (i \le l_j であるような区間を全て選んだ場合の、b_i,b_{i+1},...,b_n の最小値)$
すると、答えは
$a[i] - min(dpL[i-1],dpR[i+1])$ の全ての $i$ における最大値となります。
$dpL$ は、以下のように計算できます。
まず、連想配列などを利用して$r_j \rightarrow l_j$ をすぐに参照できるようにしておきます。
$dpL[i]$ を計算する前に、$r_j = i$ であるような全ての区間を処理します。そのような区間がない場合、$dpL[i] = min(dpL[i-1],a[i])$ です。区間があった場合、操作後に配列 $a$ を $i$ 番目まで見て、最小値を再計算すればOKです。
$dpR$ も同様の考え方で構築することができます。
計算量は、区間の1引く操作が $O(nm)$であり、最小値を求める操作が最大 $m$ 回行われるので$O(nm)$ です。よって全体の時間計算量は $O(nm)$ となります。
区間から1引く操作、区間最小値を求める操作は遅延評価セグメントツリーを用いることで高速化できるので $O(n+m\mathrm{log}n)$ まで減らすことも可能です。(pythonを利用している方はこの高速化をしないと厳しいと思います)
:::
:::spoiler **◎別解**
こちらの方が理解はしやすいと思います。
$i = 1$ の時、選んでいる区間をあらかじめ $a$ に適応しておきます。
そして、$i$ を小さい方から全探索していきます。
$i$ が最大の時の評価値は、$a[i]$の値と、$a$ 全体の最小値を調べることで求められます。ここで注意なのですが、「全体の最小値を調べる」操作は必ず $a$ が変化した直後にだけ行うことにします。
$i+1$ の評価に移るときは、$r_j = i$ である全ての区間を適用し(1減らし)、 $l_j = i$ であるすべての区間の適用を解除(1増やす)すればよいです。
各区間は最大でも2回しか $a$ の値を変更しないので、 $a$ の変更にかかる計算量は $O(mn)$ です。
区間最小値を求める操作は、先述した通り $a$ が変化した直後にだけ行うので、最大で $2m$ 回しか行いません。よって、計算量は $O(nm)$ です。
よって全体の計算量は、$O(nm)$ です。
:::
### ◎F. MST Unification
:::spoiler **◎ヒント1**
とりあえず最小全域木を求めてみましょう。
:::
:::spoiler **◎ヒント2**
最小全域木(MST) が unique でないとき、MSTに含まれる適当な辺と含まれない辺を入れ替えることで同じコストのMSTができます。
:::
:::spoiler **◎ヒント3**
元の最小全域木に、入れ替える予定の辺を付け足すとサイクルができます。
また、入れ替える相手もサイクル内の辺です。
:::
:::spoiler **◎ヒント4**
つまり、ある辺を加えるとできるサイクルに同じ重みの辺があれば unique ではありません。
また、その辺の重みはサイクル内の最大値と一致します。
:::
:::spoiler **◎ヒント5**
サイクル内に同じ重みの辺があるかは、木上のその頂点間のパスに含まれる辺の最大値を求められればよいです。
これはダブリングを用いると行えます。
:::
:::spoiler **◎ヒント6**
更に考えると、サイクル内に同じ重みがある辺の数はうまく求めることができます。
実装もダブリング等が必要なくなり軽くなります。
:::
:::spoiler **◎解説**
単純な方法だと実装することは多いですが、それぞれの部分は知っておいてもよい内容なので実装例を C++ のみで示しておきます。
ヒントが正しいものだとして、解法を示します。
ヒントの通りに最小全域木を求めた後、ダブリングによって最小共通祖先を求める方法を応用してパス上の最大重みを求められるようにします。
そしたら、最小全域木に含まれないすべての辺について、その辺が結ぶ2頂点間のパスに重みが同じものが存在しないかを調べます。
仮に存在すれば、含まれない方の辺の重みを 1 増やせばいいです。
これで、増やした重みの和を出力すると正解になります。
本当にそれだけなのか、他の考えないといけない状況もあるんじゃないだろうかと思いやすい点が多い気がするので、そのあたりの証明の概略を示しておきます。
まず、サイクルができたときに MST に含まれない辺の重みはサイクル内で最大になることですが、仮により大きい辺があったとすると、その辺と入れ替えても全域木のままですが重みが小さくなるので、元が MST であったことに矛盾します。
複数の辺を同時に入れ替えないといけないパターンがないのかも気になるかもしれません。
$e_1, e_2$ と $e_3, e_4$ を入れ替える必要があるとします。このとき、$e_1, e_2$ を取り除くと MST は A, B, C の3つの連結成分に別れ、特に $e_1$ は A, B を結んでいたとします。すると、$e_3, e_4$ のどちらかは A と B, C のどちらかを結んでいるのでそれを $e_3$ とすると、$e_1$ だけを取り除いて $e_3$ だけを加えても全域木になります。
ここで、$e_1$ の重みは $e_3$ と同じ重みです。そうでなければ入れ替えることで重みの和が小さくなってしまうため矛盾します。すると、$w_1 + w_2 = w_3 + w_4$ なので $w_2 = w_4$ です。なので、同じ重みの辺を1つ入れ替える操作 2回に分割することができるため大丈夫です。
Kruskal 法のように重みの小さい辺から見て使えるだけ使うようにすると、重み $w$ までの辺を考慮したときにできている部分グラフは使っている辺が異なったとしても連結成分としてだけ見ると同じになっています。そうでなければ、重み $w$ までの辺に、まだ連結でない成分を結ぶものが存在するからです。特に連結成分の個数も同じなので、使っている辺の個数も同じになり、どのMSTでも特定の重みの辺を使う個数は一緒です。
重み $w$ の辺集合に着目したとき、どの MST でも使用する辺の個数は同じで、逆に使用しない辺の個数も同じです。まず、重み $w$ 未満の辺で既に連結な頂点を結ぶ辺を取り除いておきます。それらはどの MST でも使われないので種類数に影響を与えません。
残った辺の中で使われなかった辺の数は同じなので、それぞれの辺を完成した MST に加えたときにできるサイクル上に重み $w$ の辺が存在することを示せばいいです。
使われなかった辺が結ぶ 2頂点 $u, v$ は、他の重み $w$ の辺によって連結になるため MST 上のパスに重み $w$ の辺を含みます。したがって、その辺を加えたときにできるサイクル上にも重み $w$ の辺が存在するとわかります。
ここまでの考察をまとめると、実は Kruskal 法の途中で重み $w$ の辺の個数を $n_w$、その中で重み $w$ 未満の辺だけで連結な頂点を結ぶ辺を $m_w$、使用することになる重み $w$ の辺の数を $use_w$ としたとき、答えに $n_w - m_w - use_w$ を足していけば答えになるためそのようにして簡潔に解くこともできます。
:::
:::spoiler **◎実装例(C++)**
```cpp=
#include <bits/stdc++.h>
using namespace std;
class UnionFind{
private:
vector<int> par;
int n;
public:
UnionFind(){}
UnionFind(int n):n(n){
par.resize(n, -1);
}
int find(int x){
return par[x] < 0 ? x : par[x] = find(par[x]);
}
int size(int x){
return -par[find(x)];
}
bool unite(int x, int y){
x = find(x);
y = find(y);
if(x == y) return false;
if(size(x) < size(y)) std::swap(x, y);
par[x] += par[y];
par[y] = x;
return true;
}
bool same(int x, int y){
return find(x) == find(y);
}
};
int main() {
int n, m;
cin >> n >> m;
using Edge = tuple<long long, int, int>;
vector<Edge> es(m);
for (int i = 0; i < m; i++) {
int u, v, w;
cin >> u >> v >> w;
u--; v--;
es[i] = Edge(w, u, v);
}
using To = pair<long long, int>;
vector<vector<To>> G(n);
// UnionFind を用いて Kruskal 法で最小全域木を求める
{
UnionFind uf(n);
sort(es.begin(), es.end());
for (auto &[w, u, v] : es) {
if (!uf.same(u, v)) {
uf.unite(u, v);
G[u].emplace_back(w, v);
G[v].emplace_back(w, u);
}
}
}
// 最小共通祖先のようにして MST 上でのパスに含まれる最大重みの辺を求める準備をする
vector<vector<long long>> par(n, vector<long long>(20, -1)), val(n, vector<long long>(20, -1));
vector<int> dep(n);
{
// ラムダ式で再帰をしている
auto dfs1 = [&](auto &&dfs1, int v, int p, int d = 0) -> void {
dep[v] = d;
for (auto &[w, u] : G[v]) {
if (u == p) continue;
par[u][0] = v;
val[u][0] = w;
dfs1(dfs1, u, v, d + 1);
}
};
dfs1(dfs1, 0, -1);
// ダブリングのためのテーブル構築
for (int k = 0; k < 19; k++) {
for (int i = 0; i < n; i++) {
if (par[i][k] != -1) {
par[i][k + 1] = par[par[i][k]][k];
val[i][k + 1] = max(val[i][k], val[par[i][k]][k]);
}
}
}
}
// 頂点 u, v のMST上パスに含まれる辺で重みが最大のものを求める
auto calc_max_edge = [&](int u, int v) {
if (dep[u] < dep[v]) swap(u, v);
long long res = 0;
// 深さを合わせる
for (int k = 19; k >= 0; k--) {
if ((dep[u] - dep[v]) >> k & 1) {
res = max(res, val[u][k]);
u = par[u][k];
}
}
if (u == v) return res;
for (int k = 19; k >= 0; k--) {
if (par[u][k] != par[v][k]) {
res = max({res, val[u][k], val[v][k]});
u = par[u][k];
v = par[v][k];
}
}
res = max({res, val[u][0], val[v][0]});
return res;
};
int res = 0;
for (auto &[w, u, v] : es) {
if (w == calc_max_edge(u, v)) {
res++;
}
}
// MST に含まれる辺を取り除く
res -= n - 1;
cout << res << endl;
}
```
:::
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet