# 時間複雜度概念、演算法介紹 2021/07/04 資訊之芽 熊育霆 --- **Outline** * 時間複雜度 * 演算法 ---- 台大資工系有一門大一必修，課名就是「資料結構與演算法」，我們花了一整個學期、每週至少三小時在學這些東西。 另一門大二必修叫做「演算法設計與分析」，一樣每週至少三小時在學這些東西。 聽一聽有興趣的同學可以參考隔壁算法班的課程。 --- {%youtube pKO9UjSeLew %} --- ## 時間複雜度是什麼 * 我們除了會[演算法](https://zh.wikipedia.org/wiki/%E7%AE%97%E6%B3%95)的正確性以外，我們也常關心這個演算法有多「好」 * 不精確地說，可以把**演算法**理解成一支程式或者完成某件事情的步驟 ---- 我們通常會用以下兩個指標來衡量一個演算法有多「好」 * 使用的時間 * 使用的空間 今天的課程主要會先著重在「時間」部份 ---- 但是直接測量一個演算法的執行時間通常不是很實際的作法(Why?) ---- ```python= def some_func(a, b): print(a) print(b) c = a + b return c ``` ---- 假設我們這樣拆解，每一行的執行時間可能會是這樣 ```python= def some_func(a, b): print(a) # cost: c1 sec print(b) # cost: c2 sec c = a + b # cost: c3 sec return c # cost: c4 sec ``` ---- 在另一台電腦上跑的時間可能會不一樣 ```python= def some_func(a, b): print(a) # cost: d1 sec print(b) # cost: d2 sec c = a + b # cost: d3 sec return c # cost: d4 sec ``` ---- 會影響一支程式執行時間的因素可能有： * 輸入（ `(a, b) = (1, 1)` 還是 `(a, b) = (10000, 10000)`?） * 機器（計算能力） * 環境（溫度、濕度） * 其他... ---- 即使如此，我們還是希望能夠衡量一個演算法的執行效率 因此需要一個方法，能夠衡量演算法的執行效率，且不被以上因素影響 --- ## 漸近符號 <img src="https://miro.medium.com/max/1200/1*j8fUQjaUlmrQEN_udU0_TQ.jpeg" alt="drawing" width="600"/> ---- 漸近符號在分析演算法效率上非常有用。以下是漸近符號家族 * $O(g(n))$ - 今天只會講這個，其他有興趣可以再來跟我討論 * $\Omega(g(n))$ * $\Theta(g(n))$ * $o(g(n))$ * $\omega(g(n))$ ---- ### $O(g(n))$ - Big-Oh Notation 中文唸作大O符號 ---- 舉個例子，假設一個演算法的執行時間（或者所需步驟數）可以用 $$T(n) = 2n^2 + n + 10$$ 表示，其中$n$為輸入的大小 ---- $$T(n) = 2n^2 + n + 10$$ 當$n$夠大的時候，除了$2n^2$以外的其他項的影響可以忽略 * $n = 10, T(n) = 200 + 10 + 10 = 220$ * $n = 100, T(n) = 20000 + 100 + 10 = 20110 \approx 2 \cdot 100^2$ * $n = 1000, T(n) = 2000000 + 1000 + 10 = 2001010 \approx 2 \cdot 1000^2$ ---- 這時我們會寫作$T(n) = O(n^2)$ 沒那麼精確地說，使用大O符號時，我們會把影響比較小的項以及係數省略 ---- 更多例子 * $T(n) = n \implies T(n) = O(n)$ * linear time 線性時間 * $T(n) = 100n^2 + 5 + \frac{1}{n} \implies T(n) = O(n^2)$ * quadratic time 二次時間（？） * $T(n) = 8763 \implies T(n) = O(1)$ * constant time 常數時間 * $T(n) = 2^n \implies T(n) = O(2^n)$ * exponential time 指數時間 --- ### 補充0 在計算機科學中，可以把大O符號理解成「描述一個函數在$n$很大時的行為」 因此我們不會說「當$n<100$時$T(n) = O(n^2)$」或是「因為可觀測的宇宙原子數量只有$10^{70}$這麼多，所以所有演算法都是$O(1)$，實作為王」等等 有興趣深入了解的可以問問一些資訊圈的同學「月球先生之亂」的故事 ---- https://blog.yangjerry.tw/2019/01/31/fibonacci-is-bigO1/ --- ### 補充1 大O符號有精確的數學定義，其中兩個等價定義如下，長到塞不下 $$f(n) = O(g(n)) \iff \limsup_{n \to \infty} |\frac{f(n)}{g(n)}| < \infty$$ $$f(n) = O(g(n)) \iff \exists c > 0, n_0 > 0\ \text{such that} \ \forall n > n_0, |f(n)| \leq |cg(n)|$$ ----  ---- 用人話來說就是對所有夠大的$n$，$f(n)$的大小會被$g(n)$的某個常數倍壓住 --- ### 生活化的例子1  ---- 假設你把備審資料放在某個置物櫃裡面，但你忘記它在哪個置物櫃中，因此你需要一一檢查每個置物櫃。假設有$n$個置物櫃，請問最壞的狀況下，你需要花多少時間才能找到備審資料？ * 假設你檢查一個置物櫃需要一秒鐘 ---- 方法：依序檢查 ```python= for i in range(n): if data_is_in(lockers[i]): return i ``` ---- 最壞的狀況：東西在最後一個你檢查的置物櫃 因此最壞需要花$n$秒 我們會說這個方法需要花費$O(n)$時間 ---- * Q1: 如果今天是你阿嬤幫你翻櫃子，每翻一個櫃子需要花費10秒鐘，而且她會在開始翻櫃子以前花5分鐘確認你吃飽了沒。在這個情況下最壞需要花$10n+300$秒，用大O符號表示的話，這個方法會花費$O(?)$時間？ ---- * Q2: 翻櫃子世界紀錄保持人來幫你檢查櫃子，他每翻一個櫃子只需要0.1秒，用大O符號表示的話，這個方法會花費$O(?)$時間？ 答案在下一頁 ---- A: 都是$O(n)$時間（線性時間） ----  ---- 唐鳳用他的腦波控制超能力來幫助你了，他可以馬上知道你的備審資料在哪個櫃子裡。 他每次使用這個超能力時需要10秒鐘充能。用大O符號表示的話，這個方法會花費$O(?)$時間？ ---- A: $O(1)$ 常數時間，因為跟輸入大小$n$無關 --- ### 生活化的例子2 假設現在這$n$個櫃子上鎖了，每個櫃子都有一把對應的鑰匙，這$n$把鑰匙全都混在一個袋子裡，你不知道哪把鑰匙對應到的櫃子是哪一個。 你每次只能用一把鑰匙去試一個櫃子，假設這個過程需要一秒鐘。打開櫃子的過程時間可以忽略不計。 ---- * 每個櫃子最爛會試到$n$把鑰匙，所以每開一個櫃子需要$n$秒 * 總共有$n$個櫃子，這樣加起來總共需要$n^2$秒 * 用大O符號來表示，我們會需要$O(n^2)$時間 --- ## 時間複雜度 - python 以下給出幾個python指令相對應的時間複雜度 (忽略位元數量) ---- * 加減乘除 - $O(1)$ * 存取一個list的某個元素 - $O(1)$ * 遍歷一個大小為$n$的list - $O(n)$ * 在大小為$n$的list位置0的地方做插入操作 - $O(n)$ * 排序一個大小為$n$的list - $O(n \log n)$ * 存取一個dictionary某個key對應到的value - $O(1)$ (What?) --- ## 時間複雜度列表 [常見時間複雜度列表](https://zh.wikipedia.org/wiki/%E6%97%B6%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6#%E5%B8%B8%E8%A7%81%E6%97%B6%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6%E5%88%97%E8%A1%A8) --- ## 演算法 接下來會介紹一些有趣的演算法 --- ### 二分搜尋法 給定一個排序好的數列，決定給定目標是否存在以及其位置 Ex. `[1, 2, 3, 5, 8, 13]`，5有沒有在這裡面？ ---- 1. 一開始先從中間切一刀 1. 看中間那個數是否是我們要的 1. 如果是，那就做完了 :smile: 1. 如果中間那個數比我們要的小，就往右邊再切一刀並回到2. 1. 如果中間那個數比我們要的大，就往左邊再切一刀並回到2. 1. 切到最後還是沒找到，那我們要的數字不在這個數列裡面 :cry: ----  ---- ```python= def binary_search(arr, left, right, hkey): while left <= right: mid = left + (right - left) // 2 if arr[mid] == hkey: return mid elif arr[mid] < hkey: left = mid + 1 elif arr[mid] > hkey: right = mid - 1 return -1 ``` ---- #### 時間複雜度分析 * 我們可以去計算總共要切幾刀 * 每次切一刀下去會淘汰掉這個數列一半的元素。 * 也就是說，假設一開始數列大小為$n$，切完一刀後只會剩下$n/2$這麼多需要檢查。 * 只剩下一個元素時直接檢查就好。 * 因此大約需要切$\log n$這麼多刀 總結來說，時間複雜度為$O(\log n)$ --- ### 泡沫排序 一個簡單暴力的排序方法 ---- ```python= def bubble_sorted(l): n = len(l) for i in range(n): for j in range(n - i - 1): if l[j] > l[j + 1]: l[j], l[j + 1] = l[j + 1], l[j] ``` ----  ---- 簡單算一下可以發現中間的nested for-loop總共會跑 $$ 1 + 2 + ... + (n-1) = n(n-1)/2$$ 這麼多次，因此時間複雜度為$O(n^2)$ ---- {%youtube lyZQPjUT5B4 %} --- ### 快速排序 ```python= print('嗨呀哭 摸都嗨呀哭') ```  ---- 快速排序法使用分治法(divide & conquer)把數列分成較小的兩個子數列，然後**遞迴**排序兩個子數列 ~~人話~~詳細作法在下一頁 ---- 快速排序步驟 1. 如果數列長度$n \leq 1$，那這個數列已經是排序好的狀態了，直接return 1. 從數列中隨便挑選一個數當作基準(pivot) 2. 依序把數列中其他數字與基準做比較，比基準小的放在左邊，比基準大或相等的放右邊 3. 對基準左邊的數列和基準右邊的數列做**快速排序** ---- 對基準左邊的數列和基準右邊的數列做**快速排序**  ---- 這就是分治法的精神：把問題分割成多個比較小的子問題解決。如果這個子問題還不夠小，就繼續切下去。 在這個演算法來說，當$n \leq 1$時可以直接解決。 ----  ---- #### 時間複雜度 快速排序的時間複雜度分析有點複雜，因此我會略過 ---- 不精確地說，期望上每次挑選基準會把數列分成大小差不多的兩塊，因此期望上加總起來會需要做$\log n$次$n$個比較 (這裡省略了非常多細節)。 ---- 結論上，平均上是$O(n \log n)$ (更精確來講是$\Theta(n \log n)$) 最糟情況會是$O(n^2)$ (why?) ---- [維基百科程式碼](https://zh.wikipedia.org/wiki/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F#%E5%8E%9F%E5%9C%B0%EF%BC%88in-place%EF%BC%89%E5%88%86%E5%89%B2%E7%9A%84%E7%89%88%E6%9C%AC) ---- 如果你還是沒有懂這個作法，可以看他們跳舞 {%youtube ywWBy6J5gz8%} --- ### 龜兔賽跑演算法 用於判斷一個鍊結串列(linked-list)是否有環  ---- * Floyd Cycle Detection Algorithm * Floyd's Tortoise and Hare Algorithm ---- #### What is a linked-list?  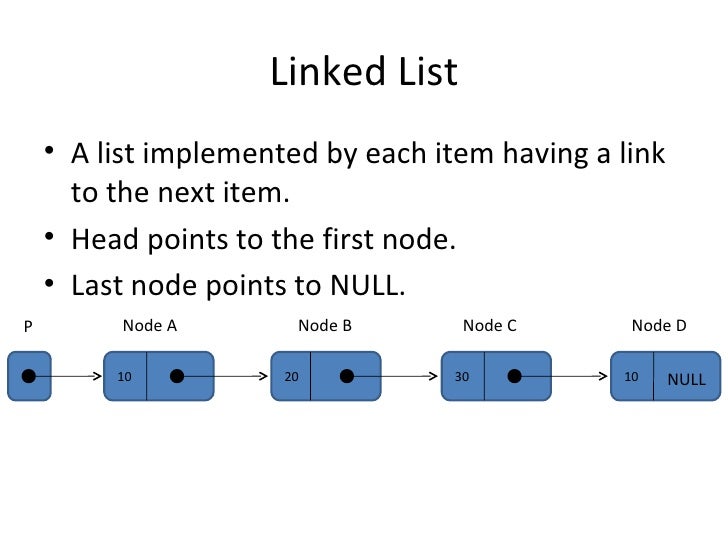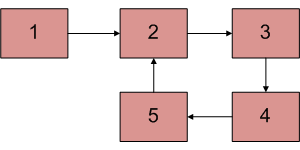---- 這就叫做一個有環的linked-list  ---- 演算法： 1. 烏龜和兔子一開始都在起點 2. 烏龜走一步，兔子走兩步，然後做以下檢查： * 如果兔子抵達終點，則此鍊結串列無環 * 如果兔子和烏龜相遇，則此鍊結串列有環 * 如果都不是，再做一次2. ---- #### 正確性分析 鍊結串列無環的情況顯然（因為兔子一定走得到終點） 以下假設鍊結串列有環 ---- * 假設鍊結串列長度為$N$，環的大小是$C>0$ * 每做一次步驟2. 烏龜和兔子的距離會增加1 * 當烏龜和兔子都進到環裡以後，最多再走$C$次步驟2.（非常粗略的估計），他們的距離總會變成$C$的某個整數倍，這時烏龜和兔子就會相遇 ---- #### 時間複雜度分析 鍊結串列無環的情況比較簡單，兔子走到終點大略需要做$N/2$次步驟2. ，因此是$O(N)$ 鍊結串列有環的狀況下，烏龜進到環裡面以後最多只能再走一圈，因此時間複雜度為$O(N)$ --- # Q & A